Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ciencias de la Salud
Print version ISSN 1692-7273On-line version ISSN 2145-4507
Rev. Cienc. Salud vol.4 no.1 Bogotá Jan./June 2006
Medidas fractales de radiografías de tórax de pacientes con diferentes patologías
Toracic X-Ray Fractal Measures in Patients with Different Pathologies
Javier Rodríguez, Signed Prieto, Catalina Correa, Nicolás Avilán, Heber Ulloa, Rubén Caicedo*
* Javier Rodríguez: MD. director del Grupo Insight.
Signed Prieto: investigadora del Grupo Insight.
Catalina Correa: psicóloga.
Nicolás Avilán: físico.
Heber Ulloa: MD. profesor asociado Departamento de Imágenes Diagnósticas, Universidad Nacional de Colombia.
Rubén Caicedo: MD. jefe del Departamento de Cirugía, Universidad Nacional de Colombia Correspondencia: Signed Prieto Diag 51 A Bis No 56 C 25 Sur. E-mail: grupoinsight2025@yahoo.es
Recibido: noviembre 30 de 2005 Aceptado: febrero 1 de 2005
Resumen
Introducción: La geometría fractal permite la descripción objetiva de objetos irregulares tales como las estructuras del cuerpo humano: Por ello, en este caso, se aplicó al desarrollo de una nueva metodología de caracterización de la cavidad cardiotorácica.
Material y métodos: Estudio exploratorio descriptivo en el que se desarrolló una metodología de medición basada en la geometría fractal aplicada a 14 radiografías de tórax de sujetos con diferentes patologías. Se calcularon las dimensiones fractales de la cavidad torácica, la silueta cardíaca y la superposición de estas partes con el método de Box-Counting.
Resultados: Se obtuvieron nuevas medidas morfométricas objetivas y reproducibles de placas de tórax a partir de dimensiones fractales.
Conclusiones: La geometría fractal permite la caracterización matemática de placas de tórax de pacientes con diferentes patologías. Es posible que el desarrollo de esta metodología en posteriores investigaciones permita generar parámetros útiles de aplicación clínica, independientes de la experiencia del médico y de su observación subjetiva, de modo que garantice la reproducibilidad y objetividad de las medidas.
Palabras clave: geometría fractal, radiografía de tórax.
Abstract
Introduction: Fractal geometry allows the objective description of irregular objects like the human body structures. In this case it was applied to the development of a new thorax cavity characterization methodology.
Materials and methods: Exploratory descriptive study where it was applied a measurement methodology based on the fractal geometry to 14 thorax x-rays from different pathologies patients. There were calculated the fractal dimensions of the thorax cavity, the cardiac silhouette and the superposition of these parts using the Box-Counting method.
Results: New objective morphometric measures of the thorax x-rays with fractal dimensions were obtained.
Conclusions: The fractal geometry allows the thorax x-rays mathematic characterization in patients with different pathologies. It is possible that the development of this methodology in later investigations allows to generate useful parameters of clinical application.
Keywords: fractal geometry, thorax x-ray.
INTRODUCCIÓN
Los fractales matemáticos son objetos abstractos en donde las partes y la totalidad son iguales a diferentes escalas. Estos objetos matemáticos han servido para caracterizar la irregularidad de los objetos naturales (1, 2). Debido a que los objetos de la naturaleza no cumplen estrictamente con las características de los fractales matemáticos, se ha desarrollado la metodología de Box-Counting para el cálculo de sus dimensiones fractales (3).
La radiografía de tórax es la técnica diagnóstica más utilizada en la clínica cotidiana para la detección y seguimiento de enfermedades cardíacas y pulmonares, pues evidencia los cambios en la morfología del corazón, el mediastino, las paredes óseas y la vasculatura pulmonar (4). Sin embargo, a pesar de que los procedimientos de evaluación actuales son de cierta utilidad clínica, no se han desarrollado métodos suficientemente objetivos para su interpretación. Ejemplo de ello es que en la actualidad la mejor indicación sobre el aumento de tamaño del corazón es tan sólo la impresión subjetiva de un lector experimentado (5, 6). Con el fin de permitir una observación más exacta, se ha desarrollado el índice cardiotorácico, según el cual el tamaño del corazón se considera normal cuando el índice cardiotorácico es menor a 0.5. Cuando éste es mayor a 0.6 indica agrandamiento cardíaco, mientras que el intervalo entre 0.5 y 0.6 es llamado área gris, pues no es posible hacer afirmaciones sobre el estado del corazón con los índices pertenecientes a este intervalo (4-7).
Actualmente, el índice cardiotorácico es la medida disponible más exacta para la evaluación del tamaño del corazón (5). Sin embargo, debido a que es un objeto irregular, no euclidiano (8, 9) es necesario desarrollar una nueva medida morfométrica objetiva a partir de una geometría adecuada al objeto de estudio, que no dependa ni de la subjetividad y ni de la experiencia del observador y que, además, permita evaluar cuantitativamente la información de las radiografías de tórax, de tal modo que aumente la efectividad diagnóstica de los métodos actuales.
Las características de la figura geométrica de la placa de tórax hacen que sea considerada como un fractal salvaje, pues hay superposición entre sus partes. Además, no es una figura autosimilar como los fractales matemáticos estrictos.
La aplicación de esta nueva metodología de medición a las placas de tórax de individuos con diferentes patologías, constituirá una primera aproximación para el posterior desarrollo de una nueva evaluación diagnóstica, con un rango de incertidumbre menor que el del índice cardiotorácico.
DEFINICIONES Y ANÁLISIS MATEMÁTICO
Fractal: Objeto irregular. Término que define irregularidad como adjetivo. Dimensión fractal: Medida numérica adimensional que caracteriza la irregularidad de los objetos.
Dimensión fractal de Box-Counting: Donde:
D: dimensión fractal.
K: grado de partición de la cuadrícula.
N: número de cuadros que contienen el contorno del objeto.
Isla: objeto fractal definido por los contornos escogidos.
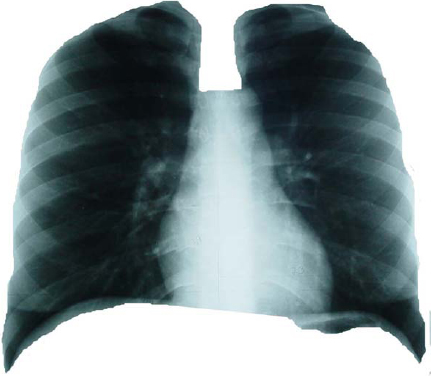
Isla 1: Isla radiopaca a la observación, limitada por los contornos dibujados en la placa detórax del ventrículo y aurícula izquierda, botón aórtico y aurícula derecha, correspondiente a la silueta cardíaca. (Ver Figura 1). Isla 2: Isla radiolúcida a la observación. Está definida por:
Isla 3: Superposición de la isla 1 con la isla
2. Objeto fractal total. Cavidad torácica completa (Ver Figura 3).
MATERIALES Y MÉTODOS
Este es un estudio exploratorio descriptivo en el que sólo se caracteriza la estructura irregular de la cavidad torácica observada a través de placas de tórax, a partir de la dimensión fractal de Box-Counting.
Se seleccionaron placas de tórax proporcionadas por el archivo docente del departamento de imágenes diagnósticas de la Universidad Nacional de Colombia en Bogotá. Las placas - en proyección P. A, correspondían a catorce pacientes con diferentes patologías, lo que permitió obtener la información suficiente para una caracterización global: dos con bullas, dos con bronquiectasias, dos con dermatomiositis, dos con neumocistis carinii, dos con tuberculosis miliar, y cuatro más con pulmón reumatoideo, LES y vasculitis séptica por pseudomona, absceso pulmonar e insuficiencia mitral, respectivamente (ver tabla 1). Las placas fueron tomadas en el hospital San Juan de Dios, en Bogotá, con el paciente en posición de pie y a una distancia de seis pies hasta el tubo de rayos, con sujeción los requisitos de la técnica radiográfica, tales como adecuada inspiración, buen centramiento y adecuada penetración.
Se calculó el índice cardiotorácico para cada radiografía, al igual que la dimensión fractal de cada una de las islas definidas en las placas. Para este último procedimiento, se requirió el diseño de dos rejillas, una con cuadros de 1.5 cm de lado y un total de 32 cuadros en el eje vertical para esta cuadrícula. La otra se construyó con 16 cuadros de 3 cm. de lado. Las rejillas fueron superpuestas a las placas y se hizo el correspondiente conteo de cuadros, lo que era necesario para hallar las dimensiones fractales mediante el método de Box-Counting, como ha sido descrito en reportes previos (10).
RESULTADOS
Se mostró que se pueden obtener nuevas medidas morfométricas objetivas de placas de tórax a partir de dimensiones fractales. Las dimensiones fractales de los objetos definidos oscilaron entre 0,99 y 1,51. Para la isla 1, las dimensiones fractales oscilaron entre 0,99 y 1,23, mientras que para la isla 2 estuvieron entre 1,05 y 1,51. Para la totalidad de la isla 3, las dimensiones fractales oscilaron entre 1,03 y 1,45 (ver tabla 2).
DISCUSIÓN
Este es el primer trabajo en el que a partir de la geometría fractal se desarrolló una nueva medida morfométrica objetiva para placas de tórax de pacientes con diferentes patologías. Se definieron tres objetos fractales denominados islas y se calcularon sus dimensiones fractales. Estas medidas matemáticas son generales, no diagnósticas, y por esto mismo no diferencian las patologías evaluadas.
La geometría fractal ha sido aplicada efectivamente a las estructuras del cuerpo humano (11- 22). Sin embargo, el cálculo de dimensiones fractales aisladas no siempre permite llegar a resultados concluyentes. Rodríguez et al (10), quienes desarrollaron una nueva metodología para superar dicha dificultad, idearon el concepto denominado Armonía Matemática Intrínseca, de manera que lograron diferenciar, en forma matemática objetiva y reproducible, las arterias coronarias sanas de las enfermas, en un modelo experimental de reestenosis que partía de la relación entre las cifras significativas de las dimensiones fractales de los componentes arteriales.
Si bien es cierto que las dimensiones fractales de las placas de tórax constituyen una nueva aproximación respecto a las medidas euclidianas tradicionales, es necesario también desarrollar una nueva metodología de medición con este tipo de geometría para su aplicación clínica, lo que permitiría comparar su efectividad con la del índice cardiotorácico.
En esta investigación se aplica una teoría matemática que caracteriza específicamente la geometría cardiotorácica de cada paciente. Por ello, el uso de herramientas estadísticas y muestras numerosas resulta innecesario, en razón de que éstas son utilizadas principalmente para validar modelos y no para aplicar un desarrollo teórico objetivo y general (22). En los modelos experimentales de reestenosis, tradicionalmente se han aplicado análisis estadísticos que han llevado a resultados con algún porcentaje de confiabilidad. Por el contrario, un análisis teórico logra diferenciaciones matemáticas entre arterias sanas y reestenosadas, sin necesidad de disponer de una población muy grande, como es requerido por los análisis estadísticos.
Es posible que las nuevas medidas morfométricas desarrolladas en esta primera aproximación, así como las que se esperan en ulteriores desarrollos, permitan generar parámetros útiles de aplicación clínica.
CONCLUSIONES
Debido a que las imágenes radiológicas de las placas de tórax son objetos irregulares, la geometría fractal es apropiada para construir una nueva metodología para la caracterización matemática objetiva de las placas de tórax. Las dimensiones fractales permiten realizar una caracterización matemática de las imágenes radiológicas de placas de tórax de pacientes con diferentes patologías. Las medidas obtenidas son independientes de la experiencia del médico y de su observación subjetiva, lo que garantiza su reproducibilidad y objetividad. La metodología desarrollada caracteriza específicamente cada placa de tórax y no requiere de un gran volumen de muestra para llegar a resultados concretos.
AGRADECIMIENTOS
Al departamento de Imágenes Diagnósticas de la Universidad Nacional de Colombia, Bogotá D.C.
Tabla 1. Diagnóstico e índice cardiotorácico de los pacientes

Tabla 2. Dimensiones fractales de las placas de tórax

Figura 1. Composición de la radiografía de tórax: Isla 1

Figura 2. Composición de la radiografía de tórax: Isla 2.
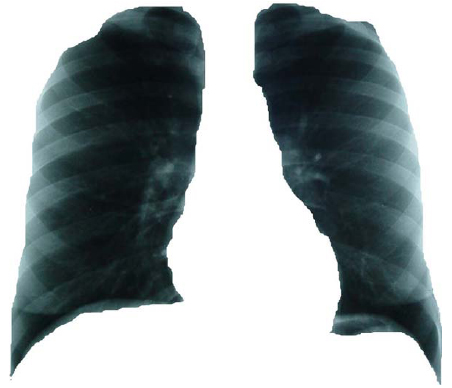
Figura 3. Composición de la radiografía de tórax: Isla 3.
BIBLIOGRAFÍA
1. Mandelbrot B. Los Objetos Fractales. Barcelona: Tusquets Eds. S.A; 2000. 2ª ed. p. 13 - 26. [ Links ]
2. Mandelbrot B. The Fractal Geometry of Nature, San Francisco: Freeman; 1972. 1ª ed. p. 341 - 348. [ Links ]
3. Peitgen H, Jürgens H, Saupe D. Chaos and Fractals: New Frontiers of Science, Springer-Verlag: NY; 1992. 1ª ed. p. 135 - 182. [ Links ]
4. Miller S. Cardiac Radiology: The Requisites, ST Louis: Mosby Year Book Inc; 1996. [ Links ]
5. Milne E, Pistolesi M. Reading the chest radiograph. A physiologic approach, St Louis: Mosby Year Book Inc; 1993. [ Links ]
6. Katz D, Math K, Groskin S. Radiology secrets. Philadelphia: Hanley & Belfus, INC; 1998. [ Links ]
7. Clark A, Coats JS. Unreability of cardiothoracic ratio as a marker of left ventricular impairment: comparison with radionuclide ventriculography and echocardiography. Postgrad Med J 2000; 895: 289 - 291. [ Links ]
8. Goldberger AL, West BJ. Fractals in physiology and medicine. Yale J Biol Med 1987; 60: 421 - 435. [ Links ]
9. Goldberger AL, Rigney D, West BJ. Chaos and fractals in human physiology. Sci Am 1990; 262: 42 - 49. [ Links ]
10. Rodríguez J, Mariño M, Avilán, N, Echeverri D. Medidas fractales de arterias coronarias en un modelo experimental de reestenosis: Armonía matemática intrínseca de la estructura arterial. Rev Col Cardiol 2002; 10: 65 – 72. [ Links ]
11. West BJ. Fractal Physiology and Chaos Medicine. En: Studies of nonlinear phenomena in life science. Vol 1. London: World Scientific Publishing Co.; 2000. 1ª ed. [ Links ]
12. Luzi P, Bianciardi G, Miracco C, De Santi MM, Del Vecchio MT, Alia L et al. Fractal Analysis in Human Pathology. Ann N Y Acad Sci 255 - 257. [ Links ]
13. H Baish J, Jain R. Fractals and Cancer. Cancer Res 2000; 60: 3683 - 3688. [ Links ]
14. Daxer A. Characterization of neovascularization process in diabetic retinopathy by means of fractal geometry: diagnostic implications. Graefe´s Arch Clin Exp Opthalmol 1993; 231: 681 - 686. [ Links ]
15. Cross SS. Fractals in pathology. J Pathol 1997; 182: 1 - 8. [ Links ]
16. Coffey DS. Self-organization, complexity and chaos: the new biology for medicine. Nat Med 1998; 4: 882 - 885. [ Links ]
17. Gazit Y, Berk DA, Leunig M, Baxter LT, Jain RK. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys Rev Lett 1995; 75: 2428 - 2431. [ Links ]
18. Landini G. Pathology in geometry, and geometry in pathology. En: Pickover CA, eds. Fractals horizonts. New York: St. Martin´s Press; 1996: 251 - 262. 1ª ed. [ Links ]
19. Cross SS. The application of fractal geometry analysis to microscopic images. Micron 1994; 25: 101 - 113. [ Links ]
20. Losa GA, Nonnenmacher F. Self similarity and fractal irregularity in the pathologic tissues. Mod Pathol 1996; 9: 174 - 182. [ Links ]
21. Paumgartner D, Losa G, Weibel ER. Resolution effect on the stereological estimation of surface and volume and its interpretation in terms of fractal dimensions. J Microsc 1981; 121: 51 - 63. [ Links ]
22. Rodríguez J, Álvarez LF, Mariño ME, Avilán G, Prieto S, Casadiego E et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Rev Col Cardiol 2004; 11: 185 - 192. [ Links ]














