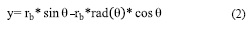http://dx.doi.org/10.15665/rp.v12i2.286.

Estado del arte sobre perfiles de dientes para engranajes

State of the art on gear tooth profiles

Pedro Nel Martínez Henao¹, Nelson Arzola de la Peña²

¹ Ingeniero Mecánico, Ph.D (c). Profesor asociado. Facultad de Ingeniería de la Universidad de San Buenaventura, Bogotá, D.C., Colombia.
² Ingeniero Mecánico, PhD. Profesor asociado. Facultad de Ingeniería de Mecánica y Mecatrónica en la Universidad Nacional de Colombia, Bogotá D.C, Colombia.
Email: pemartinez@usbbog.edu.co.

Recibido 1/04/14, Aceptado 30/06/2014

Citar como: P.N. Martinez, N.Arzola, "State of art on gear tooth profiles", Prospect, Vol 12, N° 2, 29-40, 2014.

Resumen

Este artículo resume los aspectos más importantes a tener en cuenta en el diseño de los perfiles de los dientes de engranajes, incluyendo consideraciones relacionadas con la capacidad de carga, diseño de perfil de los dientes, error de transmisión, ángulo de presión, el desgaste y el análisis de fallos. El objetivo principal de esta revisión es aportar criterios de selección para el diseño de perfiles de los dientes de engranajes rectos que ofrecen mayor capacidad y error mínimo de transmisión, por tanto esta investigación aporta una mejor comprensión del diseño basado en las variaciones geométricas del perfil de los dientes en los engranajes.

Palabras clave: Engranaje, Perfil del diente, Error de transmisión, Capacidad de carga, Análisis de falla, Ángulo presión.

Abstract

This article summarizes the most important aspects to be taken into account in the design of gear tooth profiles, including considerations related to gear load capacity, tooth profile design, transmission error, pressure angle, wear and failure analysis. The primary aim of this review is to contribute selection criteria for the design of spur gear tooth profiles that offer greater capacity and minimum transmission error, therefore this study provides a better understanding of geometric design based on variations of the gear teeth profile.

Key words: Gear, Tooth profile, Transmission error, Load capacity, Failure analysis, Pressure angle.

1. Introducción

El diseño de perfiles especiales está enmarcado dentro de una de las áreas de exploración orientada al desarrollo de sistemas de transmisión para aplicaciones específicas en gran variedad de aplicaciones industriales, las cuales emplean perfiles con diferentes características geométricas. Si bien el cálculo del perfil especial para un diseño exacto requiere de gran cantidad de operaciones matemáticas y precisión en el proceso de manufactura, sorprende ver que con los avances tecnológicos logrados en máquinas herramientas para el mecanizado de perfiles, la industria cuenta, entre otros, con equipos CNC de gran versatilidad en su programación, lo cual facilita el mecanizado de perfiles de engranaje y piezas con un alto grado de complejidad.

En este orden de ideas, en este trabajo se resalta una serie de investigaciones que sirve como marco de referencia para tener en cuenta en un diseño integral del engranaje y se describen los conceptos utilizados en los principales métodos de diseño para la generación del perfil. Por consiguiente es un tema de interés para el análisis y desarrollo de nuevos perfiles de engranajes, por lo cual su estudio requiere de muchas variables, limitaciones y relaciones que permitan lograr un perfil óptimo para una aplicación específica.

2. Contribuciones realizadas en perfiles de dientes

Considerando inicialmente la delineación del perfil de diente de involuta, Jianing [1] presenta el modelo paramétrico de engranaje de arco circular de evolvente. Las ecuaciones para el perfil de diente de involuta de arco circular están dadas por las siguientes ecuaciones paramétricas:

r_b: Radio de la base circular (m.m.)
θ: Variable independiente (radianes)

En el caso en el que se dé una configuración asimétrica del diente para el engranaje recto de involuta, la aplicación de la carga genera una desviación en el eje. Además, la carga del engranaje no se distribuye uniformemente en la línea de contacto. Como consecuencia de esto, por un lado la capacidad portante en el perfil del diente se reduce, mientras que la vibración y el ruido se amplifica durante la transmisión. Ahora bien, en un engranaje de arco circular de involuta se presentan mejores características de desempeño después de soportar carga en el perfil del diente del engranaje, la cual produce un deslizamiento relativo de forma automática y compensa la distribución no uniforme de la carga a lo largo del arco circular de contacto. Jianing [1]

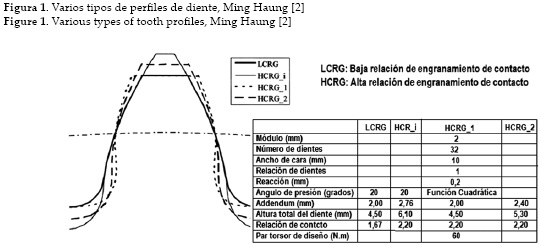
Uno de los principales aspectos a tenerse en cuenta en los sistemas de transmisión con engranajes es lograr una alta relación de contacto entre los dientes, la cual puede obtenerse incrementando el adendum del perfil del diente, sin desconocer la sensibilidad del esfuerzo que se presenta en la raíz del diente. Para minimizar estos efectos, Ming Haung [2] muestra un diseño de engranajes rectos de alto contacto que presenta una función cuadrática para el ángulo de presión, con dientes más cortos para que no se presente socavamiento (ver Figura 1). De estas circunstancias, en el modelo matemático presentado por el autor, se manifiesta que las tensiones en la raíz de los dientes y los errores de transmisión estáticos resultan ser más bajos que los de los engranajes de dientes rectos de alta relación de contacto de involuta.

El procedimiento de diseño para el perfil denominado HCRG desarrolla funciones paramétricas cuadráticas para los perfiles de los dientes; el cual permite que el piñón tenga un número relativo menor de dientes que el convencional. Se deduce que para minimizar tanto el esfuerzo de flexión en la raíz del diente como el error de transmisión se debe lograr un diente más corto que el convencional; sin embargo, la desventaja radica en que aumentan las tensiones de contacto y el desgaste en la zona de contacto. Por esta razón, una solución adecuada involucra el compromiso que exista entre la potencia a transmitir y la durabilidad de la superficie del perfil del diente. Ming Haung [2]

En relación con el concepto del trazado de la línea de acción para engranajes rectos, el modelo presentado por Zhang-Hua [3] comprende solo una curva simple de perfil de diente multisegmento, es decir, que los perfiles de los dientes de acoplamiento se pueden representar por un único parámetro de su línea de acción, lo cual hace más fácil de estudiar las características cinemáticas del engranaje con perfiles de dientes no estándar. En todo caso, vale la pena anotar que, aunque la curvatura del perfil del diente, velocidad de deslizamiento y la relación de contacto pueden derivarse de la ecuación de la línea de acción; los investigadores no realizan un análisis de los resultados experimentales referentes a esfuerzos, error de transmisión y particularidad del diseño para el trazado del perfil.

González Rey [4] Manifiesta que conocer las relaciones geométricas para el trazado del perfil de los dientes de engranajes cilíndricos permite valorar el grado de conjugación de los flancos activos de los dientes que contribuyen en gran medida a la eficiencia y efectividad de la transmisión. Ahora bien, para el trazado de la curva en la base del diente llamada trocoide, la mayoría de autores durante el modelamiento simplifican el análisis sustituyendo la trocoide por un arco de circunferencia. Otro aporte en la investigación de González Rey [4] es el trazado del perfil del diente en tres partes, (I) cresta del diente entre los puntos 1 y 2, (II) perfil del diente con trazado entre los puntos 2 y 3 cuyas coordenadas se definen en función de la geometría externa de la rueda y el flanco del borde cortante de la herramienta de generación, y (III) trazado de la curva de trocoide entre los puntos 3 y 4, según se muestra en la Figura 2. Además esta investigación plantea un algoritmo de simulación para calcular los esfuerzos en la base del diente, el cual es comparado con los resultados de los métodos que utiliza el software de Solid Edge, Cosmos Edge y los cálculos derivados de las normas ISO 6336.

Como conclusión del trabajo presentado por González Rey [4], se enfatiza en los valores cercanos de los esfuerzos actuantes en la base del diente, donde utilizando el método de los elementos finitos, los resultados muestran estar entre un 25% y un 9% mayor que los resultados que arroja la utilización del procedimiento de la norma ISO.

Sin sesgar lo citado por el autor, es lógico entender que la desviación de los resultados tiene una correlación directa al modelo geométrico del perfil del diente; ya que si el modelo geométrico no es preciso tampoco serán precisos los resultados que se obtengan con el análisis de normas ya establecidas.

Esta revisión, además, hace referencia a la aplicación imprescindible del método de los elementos finitos (MEF) utilizado como herramienta básica para el análisis del esfuerzo de contacto, capacidad de carga, rigidez de los dientes en contacto, deformaciones, etc., con base en las características de diseño que han tenido en cuenta, entre otros, autores como Sawalhi (2008), Luo, et al. [5], Yang [6], Sankar [7].

El objetivo de los sistemas de transmisión con engranajes es lograr la mayor capacidad de carga frente a su mínimo tamaño en el dimensionamiento geométrico. Asimismo se busca minimizar el ruido y la vibración del sistema de transmisión. Además, la demanda de engranajes con alta capacidad de carga busca incrementar la vida por fatiga. Atendiendo a estas consideraciones, el enfoque de diseño para aumentar la resistencia del diente en engranajes rectos expuesto por Sankar [7], quienes centran su atención en aplicar un perfil circular en la raíz del diente en lugar de utilizar un perfil trocoidal estándar, puede decirse que sus investigaciones tienden a prevenir fallas de grieta en la raíz del diente por la menor concentración de esfuerzo, dado que el esfuerzo de flexión es menor que los presentados en un filete trocoidal para la raíz del diente.

Por otro parte, el estudio de İmrek and Düzcükoğlu [8] con respecto al comportamiento entre la modificación del ancho del engranaje y el desgaste presentado según los cambios de presión a lo largo de la zona de engranamiento, realizado en engranajes fabricados en acero normalizado AISI 4140, mostró una similar distribución de la presión de Hertz a lo largo del perfil del engranaje, siempre y cuando se mantuviera una relación constante de carga aplicada a la anchura del diente (F / B) en cada punto. Las conclusiones de este estudio hacen una comparación entre los perfiles de diente para demostrar que la profundidad de desgaste a lo largo de la zona de engranamiento es casi uniforme aun en condiciones de operación a baja velocidad.

Por lo que se refiere al diseño del perfil de diente que utiliza la curva coseno como función generadora del perfil, la cual toma la línea cero de la curva de coseno como círculo de paso (ver figura 3), Luo, et al. [5], confirman que la transmisión de engranaje con función coseno tiene un coeficiente de deslizamiento inferior al perfil de evolvente y los esfuerzos de flexión y de contacto se reducen al ser comparado con el perfil de evolvente correspondiente al sistema normal de módulo, a partir de los resultados obtenidos mediante simulaciones de MEF.

Por otra parte, para el proceso de fabricación que aborda el investigador Cheng-Kang [9], se propone evitar el contacto del borde superior en un engranaje de corona cilíndrico, recurriendo al empleo de una función polinómica de cuarto orden para control del error de transmisión. La fresa generadora desarrolla la curvatura, direcciones y elipses de contacto como se muestra en la Figura 4. Se plantea que este tipo de diseño minimiza el ruido que produce la transmisión cilíndrica recta y aumenta la fuerza permisible en el perfil del diente.

A este respecto, el proceso de fabricación propuesto puede extenderse para generar un nuevo perfil por simple sustitución de la geometría del engranaje de entrada y controlando la función del error de transmisión. De manera que si se elige un polinomio de segundo orden como función de prediseño, el autor propone utilizar el mismo procedimiento planteado en la investigación para generar el nuevo perfil.

Otro tipo de diseño de perfil de diente para engranaje recto con curva de transición en forma de S es el propuesto por Abbas, et al. [10], donde se utiliza la función trigonométrica T-Bézier [G²] la cual emplea dos segmentos de la curva para la terminación del perfil del diente en lugar de cuatro segmentos como se aprecia en la Figura 5.

Sobre el asunto, los autores concluyen que utilizando la función T-Bezier se puede obtener la curva de transición en forma de S, la cual permite generar un perfil muy suave para el engranaje recto y con aplicaciones muy prometedoras para transmisión en sistemas hidráulicos.

Así mismo, Wang, et al. [11], el cual centra su trabajo en el diseño del perfil del diente; para ello, presenta un modelo matemático que incluye la ecuación de la línea de acción utilizando curvas parabólicas, la ecuación del perfil de diente y la ecuación del perfil de diente conjugado; lo anterior, sobre la base de la teoría de engranamiento. En el método propuesto, el parámetro de parábolas se toma como una de las variables de diseño para determinar el perfil del diente. Así pues, los resultados obtenidos son:

1. La forma del perfil de los dientes por encima o por debajo del círculo de paso solo es relevante para los parámetros de la parábola correspondiente. Esta propiedad permite al diseñador equilibrar el espesor de dedendum del diente.
2. El número mínimo de dientes se ve afectado por el parámetro de la parábola y se deriva de la ecuación de la línea de acción.
3. El esfuerzo de contacto y las tensiones producto de la flexión son inferiores a los que aparecen en engranajes de evolvente. Los resultados muestran que los engranajes desarrollados podrían tener aplicación en el campo de bombas de engranajes.
4. La metodología propuesta no solo se limita al empleo de curvas parabólicas. Por lo tanto, el uso de cualquier otra curva como línea de acción podría mejorar la libertad de diseño del perfil del diente para engranajes de aplicación específica.

En cuanto a la relación de transmisión, el cual es un parámetro a considerarse en los sistemas de transmisión de engranajes rectos cilíndricos, y que influye en la relación de contacto entre los perfiles de dientes a lo largo de la línea de contacto, Alipiev [12] propone un nuevo método para el diseño geométrico para los engranajes con bajo número de dientes con perfil de involuta tanto simétricos como asimétricos. De manera que los engranajes con pequeño número de dientes, en la práctica, encuentran aplicación en bombas de engranaje, aplicaciones cinemáticas que requieren de una alta relación de transmisión en engranajes para compreso-res, mecanismos para sistemas de elevación entre otros.

Así pues, el autor presenta otras ventajas del método propuesto, como:

1. Cálculo inmediato de los parámetros geométricos luego de especificar el número de dientes y la relación de contacto entre los dientes.
2. Determinación rápida del mínimo número de dientes del piñón y corona correspondiente a una específica relación de trasmisión.

No obstante las deficiencias presentadas se tienen:

1. Aumento de la velocidad de deslizamiento en los puntos de contacto, lo que provoca un aumento del desgaste en las caras de los dientes de los engranajes.
2. Aumento del esfuerzo de contacto de los perfiles a lo largo de la línea de acción

Acerca de los parámetros que se deben tener en cuenta en la fabricación del perfil del diente, la investigación de Yanmei, et al. [13] adopta un método para establecer una ecuación lineal para la superficie del diente y un engranaje imaginario conjugado. En síntesis, los resultados de esta investigación son:

Una ecuación para la superficie del diente lineal, la cual asegura un engranamiento exacto entre dientes de arco circular.

1. La ecuación de la raíz del diente, que asegura una transición suave entre las superficies de trabajo, con la cual se consigue reducir el esfuerzo de flexión en el perfil del diente.
2. Una base teórica provisional para la obtención del perfil de diente de arco circular y para el análisis de los esfuerzos de contacto en la superficie del diente.

De estas evidencias, el desarrollo de perfiles con función paramétrica para el trazado de un perfil de involuta resulta ser el más utilizado por su facilidad de mecanizado y debido a que el punto de paso siempre coincide con la línea de engranamiento. Asimismo ofrece gran ventaja sobre otros tipos de perfiles en los cuales no coincide el punto de paso con la línea de engranamiento, lo cual implica variaciones en el ángulo de presión.

3. Contribuciones sobre la capacidad de carga

En concordancia con la influencia del coeficiente de modificación del adendum sobre la capacidad de carga para engranajes con evolvente cilíndrica, la investigación de Atanasovska [14] hace una descripción de la modificación del adendum donde calcula los esfuerzos en los flancos del perfil y en la raíz del diente, haciendo uso de diagramas comparativos para facilitar la elección correcta de los valores de modificación del coeficiente del adendum, con el propósito de aumentar la capacidad de carga y reducir la vibración. Vale la pena decir que esta investigación es netamente teórica y se apoya en el empleo del software de MEF, lo cual requiere desde luego, su comprobación experimental para verificar con resultados del comportamiento de los cálculos teóricos expuestos por las investigadoras. Cabe señalar las siguientes conclusiones son obtenidas de los diagramas comparativos desarrollados en esta investigación:

1. El incremento del coeficiente de adendum conduce a la reducción de las deformaciones de los dientes.
2. La reducción de la relación de contacto , mantiene constante la suma de los coeficientes de adendum (x₁+x₂) en el piñón y la corona, lo cual conduce a una reducción en la deformación e incremento en la rigidez del diente; tal característica hace que los engranajes trabajen lentamente.
3. En todos los casos estudiados, recurrentemente se observó que la máxima tensión de contacto se presenta en un punto de la trayectoria de empalme para un periodo del engranamiento entre los dos dientes.
4. La reducción de las tensiones de contacto más significativa sucede cuando se incrementa el coeficiente x₁ del adendum en el piñón y se reduce el coeficiente x₂ del adendum de la corona.
5. La menor variación de la tensión de contacto entre dos pares de dientes se presenta para los valores de los coeficientes x₁=0.5 y x₂=0, lo cual permite una reducción de la carga de impacto.

Otro punto es el procedimiento de diseño del perfil conjugado para alta capacidad de carga presentado por Yeh [15]. En este método, la técnica de la función de desviación no uniforme (DF) se aplica para generar un nuevo perfil y se especifican los parámetros de relación de transmisión, módulo, relación de contacto, tipo de material y torque de operación.

El procedimiento puede aplicarse a cualquier tipo de perfil de paso circular y a cualquier relación de contacto. Los resultados muestran un engranaje que experimenta un reducido esfuerzo de contacto y una mayor resistencia a la flexión, además estos engranajes son capaces de llevar mayor carga que los engranajes convencionales de tamaño equivalente. Es así como el método denominado función de desviación (DF) posibilita obtener un perfil con unos esfuerzos de contacto y esfuerzo de flexión en la raíz del diente más reducidos, debido a que el esfuerzo de contacto es proporcional a la curvatura del diente y que la fuerza de flexión depende de la altura del diente. En trabajos, futuros los investigadores Yeh [15] plantea extender el procedimiento a engranajes no circulares, con el propósito de disminuir sus costos y el tamaño de las transmisiones de este tipo.

Los perfiles de dientes asimétricos presentado por Costopoulos and Spitas [16] son concebidos para rotar en una dirección, pueden ser utilizados de una manera limitada para la rotación inversa. El diseño incorpora la sustitución del filete trocoidal por un filete circular para la reducción de la concentración de tensión, lográndose un aumento del 28% en la capacidad de carga portante comparada con el perfil normal de módulo. Dicho diseño se muestra como una alternativa prometedora.

Por su parte los investigadores Pedrero, et al. [17] muestran que la rigidez del par de dientes a lo largo de la línea de acción produce una distribución de carga variable en engranajes externos de evolvente. Este modelo combina las ecuaciones de Navier y Hertz para lograr valores más realistas de las tensiones de flexión y carga por unidad de longitud en cualquier punto de la línea de contacto y para cualquier posición del engranamiento.

Por lo que se refiere al efecto que posee el cambio del radio en la raíz del diente sobre el esfuerzo de flexión. La investigación de Ashwini and Vijay [18] emplean el mismo módulo y ángulo de presión donde se analizó la distorsión que se produce en la curvatura debido a la aplicación de la carga en el punto más alto de contacto de un par de dientes empleando el MEF para su modelamiento.

A partir del análisis de los resultados de los últimos autores, se concluye que a medida que aumenta el radio de empalme de 0,5 mm a 1,5 mm, la curva de deflexión disminuye y para un radio del perfil de 1,5 mm a 2,25 mm la curva de deflexión se incrementa en engranajes con el mismo número de dientes. Además en la simulación se aprecia que el valor de desviación es mayor para ruedas dentadas con mayor número de dientes. Por ende, se concluye que el valor óptimo del radio de empalme debe ser de 1,5 mm en la raíz del diente.

Acerca del estudio de la capacidad de carga en los perfiles de los dientes del engranaje presentado por Ristivojević, et al. [19], centra la atención en la distribución de la carga, geometría del diente y desgaste en los flancos de los dientes, puede anotarse que en esta investigación se señala que el desgaste es efecto de la distribución no uniforme de carga en el perfil del diente, además se incrementa la carga dinámica y disminuye la eficiencia del engranaje. Por ello, el autor desarrolla un modelo matemático para estimar el esfuerzo de contacto en el perfil del diente.

Los resultados obtenidos muestran que el desgaste adhesivo se presenta siempre en los flancos de los dientes con mayor intensidad sobre la zona de dedendum. Además, la propiedad del engranaje depende de la precisión de fabricación, la rigidez de los dientes y la magnitud de la carga total. Es importante advertir que la intensidad del desgaste adhesivo depende principalmente de las condiciones tribológicas y del esfuerzo de contacto. Los resultados experimentales muestran que en pares de engranajes altamente cargados, los tipos de desgaste dominantes son la picadura y el desgaste adhesivo, mientras que el desgaste abrasivo es menos pronunciado.

En cuanto a la corrección dental para mejorar la capacidad portante de los engranajes cilíndricos a flexión, Machado, et al. [20] advierten sobre la importancia que tiene la prevención del fallo por rotura en la base del diente. Una forma de atenuarla es modificando el perfil del diente mediante el desplazamiento de la herramienta durante el tallado de la rueda para aumentar la capacidad portante del perfil debido a:

1. El engrosamiento del diente cerca de su base.
2. El aumento de los radios de curvatura de las superficies de la evolvente.
3. La disminución del deslizamiento específico.

Los resultados obtenidos con el aumento del coeficiente de corrección producen una disminución del valor de la tensión en la base del diente superior al 20%. Además, por cada décima de aumento del coeficiente de corrección, el espesor del diente aumenta aproximadamente un 3% para el valor del módulo utilizado.

Otro punto es el cálculo de los esfuerzos en la raíz del diente. Para tal efecto, el investigador Cotaquispe [21] plantea una ecuación de regresión multivariable no lineal para calcular el esfuerzo de flexión. La admisión de la ecuación propuesta es comparada con el esfuerzo determinado por MEF. El procedimiento consiste en calcular la curva de regresión que mejor aproxime los valores de Versus Z₁, Z₂, X₁, X₂. Luego mediante software estadístico especializado se toman las cuatro ecuaciones y se hace un análisis de regresión multivariable donde se obtiene la ecuación de regresión no lineal. La ecuación global resultante es de la forma:

Siendo:

X₁ y X₂: Factores de corrección.
C₁ a C₉: Coeficientes de la ecuación de regresión no lineal.
Z₁ y Z₂: Número de dientes del piñón y el engrane.

Con el modelo global que se muestra en la ecuación (3), se emplea un software estadístico especializado el cual permite realizar una buena aproximación en la estimación del esfuerzo de flexión por el método de superposición, teniendo en cuenta los diversos parámetros geométricos del perfil y evaluando los nueve coeficientes que definen la ecuación de regresión multivariable no lineal, obteniéndose de esta forma el modelo matemático que se muestra en la ecuación (4), para calcular los esfuerzos de flexión en el engranaje uno para cualquier relación de transmisión (Z₁/Z₂) y cualquier tipo de corrección aplicada en el engranaje (X₁/X₂)

Asi pues, los resultados encontrados por Cotaquispe [21] permite con la ecuación de regresión multivariable (3) calcular el esfuerzo de flexión en la raíz del diente, Así mismo los resultados obtenidos son muy similares al comprarlos con los métodos de elementos finitos, el cual demuestra ser un recurso de validación muy importante en el modelamiento y verificación del comportamiento de los perfiles de dientes sometidos a cargas de flexión.

4. Contribuciones sobre el estudio de los esfuerzos de contacto

Con relación a los esfuerzos de contacto en los dientes de engranajes helicoidales, los investigadores Pedrero, et al. [22] indican que la presencia de muescas en la base del engranaje pueden afectar la distribución de los esfuerzos. En estas condiciones, la relación de contacto se reduce y los puntos de contacto críticos pueden ser desplazados de su lugar. Los autores utilizan la ecuación de Hertz para el cálculo de la tensión de contacto y análisis de condiciones de carga crítica. Los resultados obtenidos muestran que la presencia de una entalladura no afecta la distribución de la carga a lo largo de la línea de contacto, excepto en el caso de engranajes que trabajan en vacío y esto ocurre cuando los puntos externos del perfil no encuentran el perfil de apareamiento debido a la presencia de un socavamiento.

Ahora bien, considerando los efectos de la fuerza de contacto de los dientes y la resistencia a la flexión presentado por Li-Shuting. [23]. El investigador emplea el MEF para hacer un análisis del contacto de los dientes cargados, la deformación, los esfuerzos de flexión y el error de transmisión. Se advierte que la tensión de contacto distribuida a lo largo de la superficie del perfil del diente es asimétrica. También el autor expone que la fórmula de Hertz no es lo suficientemente exacta para el cálculo de las tensiones de contacto en un engranaje. Por último concluye que la tensión de contacto y el error de transmisión se incrementan ligeramente si el adendum se hace más largo.

En cuanto a la utilización de ordenadores para el cálculo y diseño en ingeniería, son varios los softwares que facilitan dicha labor. Al respecto la investigación de Gopi Chand, et al. [24] utiliza el software de ¨Matlab¨ para el cálculo y diseño del perfil del diente según el sistema normal de módulo. Con respecto al cálculo de la rigidez de engranamiento en un par de engranajes rectos y grieta en la raíz del diente la investigación de Chen and Shao [25] presentan el modelamiento dinámico que permite establecer la relación entre los errores de transmisión del perfil del diente y la rigidez total del sistema de engranamiento para pares de engranajes con baja relación de contacto (LCRG), y también con pares de engranajes con alta relación de contacto (HCRG). Igualmente, se pudo establecer que los errores de transmisión se pueden disminuir con la selección apropiada del perfil del diente, para que haya una mínima amplitud fluctuante entre los perfiles, claro está con el sacrificio en la capacidad de carga. Además de la descripción de algunos de los sistemas de simulación señalados, el modelo dinámico no lineal de las transmisiones de engranajes de dientes rectos desarrollado por Fernández, et al. [26] presenta el modelo que utiliza métodos híbridos para el cálculo de las fuerzas de engranamiento, combinando un análisis de MEF y la formulación analítica, donde se presenta además un ejemplo para diferentes valores de par transmitido. En síntesis, el modelo permite una implementación simple de las desviaciones del perfil del diente para un determinado valor del par torsor, siendo capaz de predecir la holgura del cojinete, el efecto de la rigidez y el error de transmisión en los perfiles de dientes del par de engranes.

Brevemente puede decirse que en la relación de contacto, los indeseables espaciamientos entre los dientes que son causantes de oscilaciones en la velocidad, vibración y ruido. Por tanto debe buscarse que la relación de contacto entre los engranajes sea mayor que uno, para que la carga se comparta entre los dientes. Para engranajes rectos la relación de contacto puede estar entre 1 y 2; siendo el valor más aceptable cuando los engranajes tienen una relación de contacto mínimo de 1,4.

5. Contribuciones relacionadas con el estudio del ángulo de presión.

Otro aspecto que se debe tener en cuenta en el diseño de perfiles de diente es el ángulo de presión. Para tal efecto, el esfuerzo de flexión en dientes de engranaje con distribución de presión variable en superficie en el marco de la teoría planteada por Ming and Wen [27] utiliza un modelo donde se analiza la variación en la tensión de flexión para ángulos de presión normal de 14.5°, 22,5° y 30°. Así mismo se emplean respectivamente ángulos de hélice de 5°, 25°y 45°. Con estos parámetros se muestra que los engranajes con ángulos grandes de hélice o ángulos de presión más bajos presentan los mayores esfuerzos de flexión, para un valor permisible de carga dado.

Por otro lado, la metodología propuesta por Danieli [28] busca aumentar la relación de contacto entre los dientes de los engranajes no circulares, usando un ángulo de presión constante para cualquier tipo de diente. Durante la generación del perfil del diente, se encontraron problemas que atendían a la relación de contacto, debido a la forma particular del entorno de dichos perfiles. Para corregir tal problema, los autores centraron su trabajo en variar el ángulo de presión de un diente al otro, con el propósito de que la presión se mantuviera constante durante toda la superficie de contacto del diente. El trabajo presenta el modelamiento para la generación de un par de ruedas elípticas, mas no se centra en un perfil de diente en particular.

Por su parte, Spitas and Spitas [29] ha demostrado que es posible generar engranajes de evolvente utilizando un módulo no estándar y ángulo de presión de 5°, 10°, 14°, 20°, 25° según la resistencia a la flexión en engranajes de evolvente, en la cual analizan MEF, para la totalidad de valores del ángulo de presión. Como resultado se encuentra que la resistencia a la flexión en la raíz del diente tiene una relación directamente proporcional respecto al ángulo de presión.

Así pues, el ángulo de presión en un engranaje se define exactamente igual que en el mecanismo de leva y seguidor, es decir como el ángulo entre el eje de transmisión o línea de acción (normal común) y la dirección de la velocidad en el punto de paso. El ángulo de presión universalmente más comúnmente usado es el de 20°. En efecto, puede tomarse cualquier valor del ángulo de presión, pero el costo de mecanizado por el proceso y por el tipo de cortador especial que se requiere, en la mayoría de los casos no se justifica.

6. Contribuciones orientadas al error de transmisión

Otra forma de contribuir al diseño del perfil de los dientes es considerando la teoría del error de transmisión. Con esa finalidad Sommer, et al. [30] muestra que la holgura radial entre los dientes de los engranajes es esencial para proporcionar una mejor lubricación en la superficie de los dientes; por un lado la vibración torsional causa separación de los dientes, dado que elimina la interferencia que se incluye como un defecto y que es una parte necesaria del diseño de la transmisión. Por otra parte, el error en la geometría del diente o rotura en el diente provoca un retraso en las fuerzas de contacto de los perfiles.

Así mismo, observando los efectos del error de transmisión como consecuencia de los errores de mecanizado y de montaje en engranajes de dientes rectos, el investigador Li-Shuting. [31] hace un análisis de estos parámetros y sugiere que para tener una alta resistencia del engranaje, la desalineación entre los ejes de los engranajes no debe ser mayor a 0,01°y que la holgura entre dientes debe estar entre 10 µm a 20 µm. En efecto, también se demuestra que al sobrepasar estos valores, se presentan cambios en la forma de onda del error de transmisión.

Prosiguiendo con el tema, el estudio adelantado por Hotait [32] proporciona un conjunto de datos experimentales del error de transmisión fundamentado en la relación entre el error estático y el error de transmisión dinámico en los dientes de un engranaje recto. De igual modo, se completa el estudio en términos de establecer la relación entre la durabilidad y la medida del ruido generado por el engranamiento de los dientes.

La medición tanto del factor dinámico (DF) como del error de transmisión dinámico (DTE) se realiza en un rango de frecuencias, que incluye la frecuencia natural a la torsión de los pares de engranajes. Los datos son comparados entre sí y los resultados indican que existe una relación lineal entre las dos; lo cual posibilita que uno se pueda estimar mediante la medición del otro.

Es interesante examinar el problema de distribución de la carga en dientes considerando el error de transmisión estático (TE) desde la perspectiva planteada por Wink and Serpa [33], exponen tres procedimientos para evaluar la distribución de la carga en los engranajes, como son: (I) el cálculo computacional empleando el método de comparación, (II) el procedimiento de carga gradual e iterativo y (III) el método de seudo-interferencia. Este último procedimiento se resolvió mediante programación lineal, solución basada en un algoritmo de punto interior y un solucionador de matriz directa basada en la factorización de Colesky. Es así como el método de seudo-interferencia muestra ser muy eficaz en la solución a los problemas de distribución de carga de los dientes de los engranajes.

7. Contribuciones en el análisis de falla

Con respecto al efecto del contacto entre dientes y su aplicación en la reducción de la fatiga en el desgaste del perfil del diente por picadura, la investigación de Mao [34] emplea tres tipos de perfiles de dientes con modificaciones de micro geometría en condiciones de carga real para proporcionar una visión cuantitativa del comportamiento del contacto de los dientes bajo el efecto de la desalineación y deformación del eje. Aunque no se muestran mayores aportes para el desarrollo de nuevos perfiles, si se esboza un procedimiento para simular el contacto de los dientes mediante el empleo de MEF.

En relación a los efectos de la fricción entre los perfiles de dientes, vale destacar la investigación de Zheng and Ken [35] en la cual señala que la fricción es un efecto del contacto entre los perfiles de dientes y que la fricción de deslizamiento es una de las principales razones que causan fallo por el contacto de los perfiles en los trenes de engranaje. Como conclusiones de esta investigación se puede destacar:

1. La fricción puede disminuir el esfuerzo de flexión durante la primera fase del contacto, pero el esfuerzo de flexión se incrementa durante la segunda fase del
2. El esfuerzo de flexión depende del coeficiente de fricción entre las superficies en contacto y el torque de entrada.
3. El efecto de la fricción sobre el error de transmisión cambia gradualmente durante la marcha y presenta modificaciones para altas cargas de trabajo.
4. En síntesis, la fricción es un factor fundamental que se debe tener en cuenta durante la fase de diseño y su incidencia en los esfuerzos de flexión debe ser considerada en el análisis de la resistencia del diente.

Así mismo, hay que tener en cuenta las normas establecidas por la American Society for Metals [36] que hacen referencia al análisis de falla que presenta los sistemas de transmisión con engranajes. El desgaste en el engranaje es producto de una combinación de factores que actúan sobre el perfil del diente. La vida útil está en función de diversas fuerzas o cargas. Si la rapidez del desgaste se conoce o puede estimase a partir de los datos, es posible construir un conjunto de límites de control sesgados en torno de la línea de la tendencia de desgaste del perfil del diente. La relación entre el desgaste y la modificación del espesor del diente en engranajes rectos correspondiente al estudio experimental hecho por İmrek and Düzcükoğlu [8] logra, aproximadamente igual distribución de presión de Hertz a lo largo del perfil. En torno a estos elementos señalados, deshacerse de los cambios de presión instantánea es obtener control sobre algunos de los parámetros que afectan el desgaste de los engranajes.

Esta revisión, nos lleva a considerar el método para prevenir la ocurrencia prematura de picadura en engranajes de dientes rectos presentado por Düzcükoğlu and İmrek [37]. El autor señala que la picadura en la superficie del diente es una de las causas más comunes de fallo operativo en el engranaje. Para mitigarlo, el autor propone la disminución de la tensión superficial mediante el aumento del ancho del diente. Adicionalmente, encontraron que la formación de picadura es más rápido en engranajes con alto par de transmisión

Por lo que se refiere a la iniciación de la propagación de grietas por fatiga debida al contacto cíclico expuesta por Fajdiga and Sraml [38], quienes adelantan un modelo computacional que considera, primero, un periodo de iniciación de la grieta y, posteriormente, un periodo de propagación de la grieta. En el modelo se considera un material homogéneo y elástico y utiliza el MEF para modelar la propagación de grieta por fatiga. Este modelo aparenta ser apropiado para determinar la vida útil de los engranajes. Hay que tener en cuenta que el modelo no incluye algunos aspectos involucrados frecuentemente en los análisis de falla por fatiga como son las dislocaciones, las impurezas y las tensiones residuales.

De otro lado, Imrek and Unuvar [39] muestran que la carga y la velocidad de rotación son factores que influyen en la generación de escoriado en el adendum del perfil de un diente modificado. Son muchos los factores que producen escoriado, por lo cual la investigación en cuestión utiliza distintas velocidades de operación y diferentes niveles de carga con variaciones en el adendum. Esto lleva a probar que el escoriado como agente de desgaste aumenta cuando mayor es el adendum del perfil del diente, teniendo dicho desgaste una relación directa con la velocidad de rotación y la potencia transmitida.

Donzella and Petrogalli [40] desarrollaron un diagrama para la evaluación de la zona de trabajo segura de componentes sometidos a rodadura, siguiendo el modelo de EI-Haddad para el cálculo del umbral de crecimiento de grieta. De manera particular, el diagrama presenta diferentes zonas: una zona segura (vida infinita), una zona de fatiga, y otra zona de fractura estática. En esta investigación se resalta la importancia de tener una adecuada lubricación entre las superficies en contacto en condiciones de rodadura; de la misma manera es importante lograr una dureza superficial, dado que este factor juega un papel importante en la definición de la ubicación de la propagación de grietas.

Otro estudio relacionado con la predicción de la fatiga por contacto por rodadura es el que presentan Beheshti and Khonsari [41]o. En su trabajo, el autor aplica un enfoque moderno en mecánica para predecir el inicio de grieta por fatiga de contacto utilizando la teoría de Hertz. El modelo es capaz de calcular la variable de daño utilizando las propiedades de los materiales y las condiciones de la superficie. Se infiere que esta investigación presenta inconvenientes como los expuestos en el trabajo de Fajdiga and Sraml [38], donde se expone que los esfuerzos deben dirigirse al desarrollo de un modelo de predicción del daño más generalizado para la fatiga por contacto con la consideración del efecto de la secuencia de variación de carga.

Además de describir los parámetros relacionados con el análisis de falla, en el trabajo de Osman and Velex [42] se presentan modelos para describir las interacciones entre cargas dinámicas y la fatiga por contacto entre dientes de engranajes rectos. Esta situación representa el inicio de la propagación de grieta, aunque el enfoque se limita a problemas bidimensionales, también vincula criterios de fatiga y las cargas son muy influyentes en función del rango de velocidad, ya que pueden inducir daños por fatiga en ciertos puntos del perfil del diente.

También es importante mencionar el trabajo sobre micro picadura de contacto en engranajes rectos presentado por Li and Kahraman [43], los cual proponen un modelo para predecir el comportamiento de micro picadura en las superficies de contacto en engranajes bajo la condición de lubricación elastohidrodinámica mixta transitoria. En términos simples, este tipo de lubricación es cuando las superficies en contacto cambian de forma elástica y la película de lubricación atrapada entre las superficies provee una lubricación hidrodinámica microscópica. Las evidencias arrojan una nueva formulación de elementos de contorno para la línea de contacto en superficie rugosa, la cual permite calcular la tensión multiaxial para evaluar la fatiga por micro picadura. El modelo se encuentra en su fase de validación mediante la confrontación experimental de fatiga por contacto.

Otros autores, mediante el análisis experimental, estudian el comportamiento de la rigidez del diente con presencia de grieta. Es así como Pandya and Parey [44] emplean la técnica de fotoelasticidad para medir la variación de la rigidez en el diente. El procedimiento para calcular la rigidez del diente se basa en la energía de deformación liberada para un diente sin grieta y otro diente con grieta, para diferentes posiciones de contacto.

En resumen, son muchas los modos de falla que se presentan en los engranajes los cuales son producidos por causas bien sea por condiciones de carga, operación o por condiciones ambientales que aceleran el deterioro superficial o la micro estructura del diente. Por tanto en la fase experimental estas son variables que influyen y deben controlarse dentro de los rangos permisibles, además existen varios procedimientos para realizar dichos registros y medición de dichas variables.

8. Conclusiones

• Una de las tendencias de desarrollo más generalizada en el diseño de perfiles es recurrir al empleo de ayudas computacionales para el diseño y manufactura -CAD-CAM, los cuales permiten gran flexibilidad en cuanto a los parámetros deseados por el diseñador y a las restricciones de operación del sistema de transmisión.
• El principal factor que incide en el comportamiento dinámico del engrane es la variación de la rigidez del diente, la cual bajo momentos en el piñón Mp y en el engranaje Mg constantes, provocará fuerzas de engrane Fm variables en el tiempo que se transmiten a los descansos y finalmente generan las vibraciones. La frecuencia de las vibraciones generadas corresponde a múltiplos de la frecuencia de engrane.
• Es posible introducir en el modelo problemas en las superficies de los dientes mediante funciones de error, las cuales representan la diferencia entre el perfil sin problemas y el perfil dañado.
• Son varios los factores que deben ser considerados en el diseño de perfiles de dientes para engranajes, como lo son la función que rige la geometría del perfil del diente, la magnitud de su capacidad de carga portante, los esfuerzo en el diente y vida útil entre otros. Esto conduce a tener unos parámetros bien definidos al momento de hacer un análisis de falla, según las condiciones de operación del sistema de transmisión.
• A modo de recomendación, los investigadores interesados en estos temas pueden incursionar en los siguientes campos:
• Estudio de los perfiles modificados que compensen las distorsiones del diente bajo carga y lograr diseños de engranajes con mayor capacidad de carga portante.
• Investigar sobre los procesos de fabricación y clases de herramientas para la generación de los perfiles de dientes.

Referencias

[1] H. W. Jianing, Zhang., "Optimum Design and Research on the Involute Gear Tooth Profile," International Conference on Electronic & Mechanical Engineering and information Technology, p. 4, 2011.         [ Links ]

[2] T. Y. C. Ming Haung, Tsai., "Design of high contact ratio spur gears using quadratic parametric tooth profiles," Mechanism and Machine Theory, vol. 33, pp. 551-564, 1998.         [ Links ]

[3] F. T.-W. Zhang-Hua, Chiang.Chieh, Wen Tsay., "Mathematical Model for Parametric Tooth Profile of Spur Gear Using Line of Action," Mathematical and Computer Modelling vol. 36, pp. 603-614, 2002.         [ Links ]

[4] G. González Rey, "Relación geometrica para trazado del perfil de los dientes de negranajes cilíndricos," CUJAE, Facultad de Ingeniería Mecánica. Cuba, 2005.         [ Links ]

[5] S. Luo, Y. Wu, and J. Wang, "The generation principle and mathematical models of a novel cosine gear drive," Mechanism and Machine Theory, vol. 43, pp. 1543-1556, 2008.         [ Links ]

[6] S.-C. Yang, "Mathematical model of a stepped triple circular-arc gear," Mechanism and Machine Theory, vol. 44, pp. 1019-1031, 2009.         [ Links ]

[7] S. N. Sankar, Muthusamy., "Profile modification-a design approach for increasing the tooth strength in spur gear," The International Journal of Advanced Manufacturing Technology, vol. 55, pp. 1-10, 2010.         [ Links ]

[8] H. İmrek and H. Düzcükoğlu, "Relation between wear and tooth width modification in spur gears," Wear, vol. 262, pp. 390-394, 2007.         [ Links ]

[9] L. Cheng-Kang, "Manufacturing process for a cylindrical crown gear drive with a controllable fourth order polynomial function of transmission error," Journal of Materials Processing Technology, vol. 209, pp. 3-13, 2009.         [ Links ]

[10] M. Abbas, S. H. J. a. Yahaya, M. Ena, A. Ahmad, and J. M. Ali, "Spur Gear Tooth Design and Transition Curve as a Spiral Using Cubic Trigonometric Bezier Function," pp. 76-81, 2011.         [ Links ]

[11] J. Wang, H. Liang, S. Luo, and R. Y. Wu, "Active design of tooth profiles using parabolic curve as the line of action," Mechanism and Machine Theory, vol. 67, pp. 47-63, 2013.         [ Links ]

[12] O. Alipiev, "Geometric design of involute spur gear drives with symmetric and asymmetric teeth using the Realized Potential Method," Mechanism and Machine Theory, vol. 46, pp. 10-32, 2011.         [ Links ]         [ Links ] 2013.

[14] I. N.-S. Atanasovska, Vera., "Influence of addendum modification coefficient on the gear load capacity," Faculty of Management in Industry, JNA 63, 37000 Krusevac, Serbia., 7, 2006.         [ Links ]

[15] T. C. H. Yeh, Daniel. Tong, Shih-Hsi. , "Design of new tooth profiles for high load capacity gears," Mechanism and Machine Theory, vol. 36, 2001.         [ Links ]

[16] T. Costopoulos and V. Spitas, "Reduction of gear fillet stresses by using one-sided involute asymmetric teeth," Mechanism and Machine Theory, vol. 44, pp. 1524-1534, 2009.         [ Links ]

[17] J. I. Pedrero, M. Pleguezuelos, M. Artés, and J. A. Antona, "Load distribution model along the line of contact for involute external gears," Mechanism and Machine Theory, vol. 45, pp. 780-794, 2010.         [ Links ]

[18] J. Ashwini and K. K. Vijay, "Effect on Strength of Involute Spur Gear by Changing the Fillet Radius Using FEA," International Journal Of Scientific & Engineering Research, vol. 2, 2011.         [ Links ]

[19] M. Ristivojević, T. Lazović, and A. Vencl, "Studying the load carrying capacity of spur gear tooth flanks," Mechanism and Machine Theory, vol. 59, pp. 125-137, 2013.         [ Links ]

[20] A. Machado, J. Moya, and L. Negrín, "Análisis de la influencia de los desplazamientos en la capacidad portante de los engranajes cilindricos a flexion," 2001.         [ Links ]

[21] Z. L. O. Cotaquispe, "Influencia de los parametros geométricos para la obtención de un modelo matemático estable para el cálculo de los esfuerzos en la raíz del diente," Facultad de Ciencias e Ingeniería, Pontificia Universidad Católica del Perú, 2006.         [ Links ]

[22] J. Pedrero, M. Pleguezuelos, and M. Muñoz, "Contact stress calculation of undercut spur and helical gear teeth," Mechanism and Machine Theory, vol. 46, pp. 1633-1646, 2011.         [ Links ]

[23] Li-Shuting., "Effect of addendum on contact strength, bending strength and basic performance parameters of a pair of spur gears," Mechanism and Machine Theory, vol. 43, pp. 1557-1584, 2008.         [ Links ]

[24] A. Gopi Chand, A. Sharma, K. Pavan Kumar, and I. A. Sainath, "Design of Spur Gear and its Tooth profile," Journal of Engineering Research and Applications (IJERA), vol. 2, pp. 2248-9622, 2012.         [ Links ]

[25] Z. Chen and Y. Shao, "Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack," Mechanism and Machine Theory, vol. 62, pp. 63-74, 2013.         [ Links ]

[26] A. Fernández, M. Iglesias, A. de-Juan, P. García, R. Sancibrián, and F. Viadero, "Gear transmission dynamic: Effects of tooth profile deviations and support flexibility," Applied Acoustics, vol. 77, pp. 138-149, 2014.         [ Links ]

[27] H. C. Ming and J. W. Wen, "Bending stress in gear teeth for variable surface pressure distribution.pdf," Mathematical analysis and applications, vol. 167, pp. 182-202, 1992.         [ Links ]

[28] G. A. M. Danieli, D., "New developments in variable radius gears using constant pressure angle teeth," Mechanism and Machine Theory, vol. 40, pp. 203-217, 2005.         [ Links ]

[29] C. Spitas and V. Spitas, "Effect of Cutter Pressure Angle on the Undercutting Risk and Bending Strength of 20° Involute Pinions Cut with Equivalent Nonstandard Cutters#," Mechanics Based Design of Structures and Machines, vol. 36, pp. 189-211, 2008.         [ Links ]

[30] A. Sommer, J. Meagher, and X. Wu, "An Advanced Numerical Model of Gear Tooth Loading from Backlash and Profile errors," p. 14, 2010.         [ Links ]

[31] Li-Shuting., "Effects of machining errors, assembly errors and tooth modifications on loading capacity, loadsharing ratio and transmission error of a pair of spur gears," Mechanism and Machine Theory, vol. 42, pp. 698-726, 2007.         [ Links ]

[32] M. A. K. Hotait, A., "Experiments on the relationship between the dynamic transmission error and the dynamic stress factor of spur gear pairs," Mechanism and Machine Theory, vol. 70, pp. 116-128, 2013.         [ Links ]

[33] C. H. Wink and A. L. Serpa, "Performance assessment of solution methods for load distribution problem of gear teeth," Mechanism and Machine Theory, vol. 43, pp. 80-94, 2008.         [ Links ]

[34] K. Mao, "Gear tooth contact analysis and its application in the reduction of fatigue wear," Wear, vol. 262, pp. 1281-1288, 2007.         [ Links ]

[35] L. Zheng and M. Ken, "Frictional Effects on Gear Tooth Contact Analysis," The Gearbox Research Institute, Dalian Huarui Heavy Group Co., Ltd., p. 13, 2009.         [ Links ]

[36] I. ASM, General Procedures for Failure Analysis, 2002.         [ Links ]

[37] H. Düzcükoğlu and H. İmrek, "A new method for preventing premature pitting formation on spur gears," Engineering Fracture Mechanics, vol. 75, pp. 4431-4438, 2008.         [ Links ]

[38] G. Fajdiga and M. Sraml, "Fatigue crack initiation and propagation under cyclic contact loading," Engineering Fracture Mechanics, vol. 76, pp. 1320-1335, 2009.         [ Links ]

[39] H. Imrek and A. Unuvar, "Investigation of influence of load and velocity on scoring of addendum modified gear tooth profiles," Mechanism and Machine Theory, vol. 44, pp. 938-948, 2009.         [ Links ]

[40] G. Donzella and C. Petrogalli, "A failure assessment diagram for components subjected to rolling contact loading," International Journal of Fatigue, vol. 32, pp. 256-268, 2010.         [ Links ]

[41] A. Beheshti and M. M. Khonsari, "On the prediction of fatigue crack initiation in rolling/sliding contacts with provision for loading sequence effect," Tribology International, vol. 44, pp. 1620-1628, 2011.         [ Links ]

[42] T. Osman and P. Velex, "A model for the simulation of the interactions between dynamic tooth loads and contact fatigue in spur gears," Tribology International, vol. 46, pp. 84-96, 2012.         [ Links ]

[43] S. Li and A. Kahraman, "A micro-pitting model for spur gear contacts," International Journal of Fatigue, vol. 59, pp. 224-233, 2014.         [ Links ]

[44] Y. Pandya and A. Parey, "Experimental investigation of spur gear tooth mesh stiffness in the presence of crack using photoelasticity technique," Engineering Failure Analysis, vol. 34, pp. 488-500, 2013.         [ Links ]