1. INTRODUCCIÓN
En los grandes procesos químicos de la industria se generan enormes cantidades de calor que debe ser removido para que todas las unidades operen eficientemente. Los equipos de transferencia de calor más comúnmente utilizados son los intercambiadores de calor y condensadores. Muchas compañías requieren tener procesos eficientes en cuanto al costo razón por la cual gran cantidad del agua que se usa en muchos intercambiadores de calor para refrigerar es recirculada y reutilizada. Para lograr esto una de las formas más prácticas y económicas es mediante el uso de torres de enfriamiento empacadas, ya que ofrecen ventajas importantes por la transferencia simultánea de calor y masa debida a que el contacto entre los fluidos es directo. Una ventaja que tienen las torres de enfriamiento sobre los intercambiadores de calor comunes es la gran cantidad de agua que manejan debido a que pueden tratar toda el agua de una planta entera mientras que los intercambiadores comunes son utilizados para equipos simples (1, 2). La eficacia de las torres se debe a que estas ayudan a que el área superficial de contacto entre los medios sea alta intensificando el transporte de masa y energía. En la actualidad existen tres tipos de empaques que son los más usados, los cuales son, de película, salpicadura (splash) y de malla-película 3.
Con el fin de optimizar el desempeño de estos equipos en estos últimos años se han llevado a cabo investigaciones experimentales acerca de los parámetros que tienen más influencia en la transferencia de calor y masa, en especial el tipo de empaque. Simpson y Sherwood 4 estudiaron el desempeño de una torre de enfriamiento de tiro mecánico utilizando empaques de listones de madera. Kelly y Swenson 5 estudiaron las características de un empaque de tipo malla correlacionando la relación de flujo agua/aire con otras variables como el cambio en la temperatura del agua y la geometría del empaque. También encontraron un valor dado de la relación L'/G'en el que las características del equipo se volvían independientes de la temperatura de bulbo húmedo y el flujo de aire. Bedekar et al. 3 Realizaron estudios experimentales con empaques peliculares y presentaron sus resultados en términos de las características de la torres como la temperatura de salida del agua y la eficiencia como función de la relación de flujo L'/G'.
Las correlaciones empíricas para los coeficientes de transferencia de calor y masa (Kya) aparecen en distintos formatos en varios estudios. Lowe 6 presentó la correlación de la forma como está en la ecuación (1), mientras que Kloppers y Kroger 7 de la forma como se muestra en la ecuación (2).
En otros estudios Kloppers y Kroger (8) notaron que el coeficiente de transferencia Kya también dependía de la altura del empaque, y de la variación de la temperatura de entrada, sugiriendo una nueva forma de correlación como es la mostrada en la ecuación (3).
Siendo los valores de c constantes en las relaciones empíricas para los diferentes tipos de empaque.
Trabajos como los de Bedekar 3 et al., de Gharaghezi y Missenden 9, Kloppers y Kroger 10, han reportado que los efectos de la relación del flujo de líquido y gas, la temperatura de entrada del agua, así como tamaño del empaque utilizados, son extremadamente importantes en el desempeño de la misma. Con esto se han desarrollado correlaciones empíricas de factores como el coeficiente de transferencia de calor y masa ( K y a) y la eficiencia, con respecto a las variables mencionadas, para obtener datos que permitan diseñar torres de enfriamiento empacadas más eficientes. Otro estudio investigó el efecto de empaques tipo salpicadura en un eje rotatorio, sus resultados mostraron que el calor rechazado por el equipo aumenta conforme la velocidad rotacional 11. También se investigó el efecto en el desempeño de torres de enfriamiento industriales de los defectos causados por mal mantenimiento en diferentes partes de las torres de enfriamiento industrial como boquillas de aspersión y bloqueos en empaques 12. Otros investigadores realizaron un estudio experimental en empaques de PVC donde se varía el número de láminas y obtienen correlaciones empíricas para determinar el punto óptimo de operación 13.
Sin embargo, a pesar de lo valioso de los resultados, estos han sido muy específicos con respecto al tipo de material de empaque, por lo cual en el presente trabajo se construyó una torre de enfriamiento a escala de laboratorio y se utilizaron empaques de tipo salpicadura de cuatro materiales diferentes: madera, plástico acrílico, aluminio, hierro y uno de tipo película hecho de plástico acrílico los cuales se dimensionaron de acuerdo con los parámetros de diseño encontrados en el trabajo de Mohiuddin A.K.M. et al. 14. De esta manera se hizo el estudio del comportamiento de los coeficientes de transferencia de masa y de calor relacionados a los procesos de humidificación para diferentes factores de material del empaque, la relación L'/G'y la temperatura de entrada del líquido, para determinar así su influencia en la eficiencia del equipo y como también la mejor combinación de parámetros que permitan una alta transferencia de calor y masa.
2. METODOLOGÍA
Para el diseño de torres de enfriamiento con relleno se utilizan ecuaciones empíricas como las siguientes, que determinan la altura de empaque utilizando el parámetro 𝐾 𝑦 𝑎V/L y el método de Merkel 15 otros valores constantes específicos para cada tipo de relleno 14.
Donde, A y p son parámetros contantes para cada empaque y se encuentran tabulados, L'/G'es la relación de flujos másicos del agua y aire, ND es el número de pisos de la torre, H es la altura del empaque y VDS el espaciado entre pisos del empaque. Se realizó el diseño de la torre de enfriamiento a escala de laboratorio, tomando como referencia parámetros establecidos en la revisión bibliográfica.
Para realizar los cálculos se asumen condiciones iniciales de operación, 4,9,16, las cuales se muestran en la siguiente tabla 1. Una vez realizados los cálculos se obtienen las dimensiones de la torre de enfriamiento como se muestra en la tabla 2. Para el empaque de tipo película se construyeron 3 piezas de 0,15 m de altura, cada una de estas con 5 láminas de dimensiones mostradas en la figura 1b, para un total de altura de empaque de 0,45 m.
Tabla 1 Condiciones de diseño y altura calculada para la torre de enfriamiento empacada.
| Propiedad | Valor |
|---|---|
| Temperatura de entrada del agua (T) | 45°C |
| Temperatura de salida del agua (T) | 35°C |
| Temperatura de bulbo seco del aire entrada (Tbs1)a | 30°C |
| Temperatura de bulbo húmedo del aire entrada (Tbh2)a | 28°C |
| Flujo de entrada de agua (QL) | 1,5 L/min |
| Flujo volumétrico de entrada de aire (QG)b | 2,97 m3/min |
| Lado de la torre c | 0,15 m |
| Altura de empaque calculada | 1,14 m |
Tabla 2 Dimensiones de la torre de enfriamiento.
| Parámetro | Dimensión | Parámetro | Dimensión |
|---|---|---|---|
| Número de pisos empaque tipo salpicadura | 4 | Altura total de empaque | 1,41 m |
| Espaciado entre empaques tipo salpicadura | 0,38 m | Altura total de la torre | 1,54 m |
| Número de pisos empaque tipo película | 3 | Ancho | 0,15 m |
| Espaciado entre empaque tipo película | 0,20 m | Largo | 0,15 m |

Fuente: A. K. M. Mohiuddin and K. Kant, 1996. 14
Figura 1 Dimensiones (en mm) del empaque tipo salpicadura (a) y tipo película (b). 14
Se construyeron rellenos tipo salpicadura hechos de distintos materiales: madera, aluminio, acrílico y hierro (ver figura 1a y figura 2).

Fuente: El autor
Figura 2 Empaques tipo salpicadura utilizados en la torre de enfriamiento. Tipos de material: Madera (a), aluminio (b), hierro (c) y acrílico (d).
También se tomó en cuenta un empaque tipo película de acrílico como se puede observar en la figura 3. con el fin de comparar la influencia de la forma de este con los demás 14.
En la figura 4 se muestra el diagrama de tuberías y accesorios del montaje de la torre de enfriamiento, todas las líneas y accesorios (codos y reducciones) de material PVC, a excepción de las válvulas V-1/2 las cuales son de bronce y tipo globo. Además, en la Tabla 3 se expone información relevante con respecto a los equipos de la torre e instrumentos de medición y control empleados para la construcción del sistema.
Tabla 3 Descripción equipos e instrumentación.
| Equipos | ||||
|---|---|---|---|---|
| Nombre | TAG | Tamaño | Temperatura Diseño | |
| Extractor de aire semi-industrial 8'' | E-1 | (1/12 HP) | 30 °C | |
| Bomba sumergible | P-1 | 30 W | 40°C | |
| Bomba centrifuga | P-2 | 70-140 W | 50°C | |
| Resistencia sumergible | R-1 | 3,5 kW | 50°C | |
| Tanque 1. Agua de reposición | T-1 | 50 L | 40°C | |
| Tanque 2. Agua caliente | T-2 | 50 L | 50°C | |
| Instrumentos | ||||
| Nombre | TAG | Rango | Temperatura Diseño | |
| Anemómetro digital | A-1 | 0-30 m/s | 45 °C | |
| Sensor de temperatura digital 1. Tope de la torre | TS-1 | 0-100 °C | 100°C | |
| Rotámetro | RT-1 | 0-9,46 lpm | 60°C | |
| TAG | Set-point | Acción del actuador | ||
| Sistema de control de temperatura On/Off con termopar | TC-1 | 48-40°C | Inversa | |
El procedimiento de experimentación fue el siguiente: con el tanque de agua de entrada (T-2) lleno, se encendió el sistema de control de temperatura en conjunto con la resistencia eléctrica, ajustándolo en el set-point deseado. Este tanque posee un agitador de paletas impulsado por un motor eléctrico para la lectura correcta de la termocupla en el sensor/controlador. Se toman datos de las condiciones ambiente, la temperatura de bulbo seco y bulbo húmedo. Luego, se enciende el extractor de aire y con el anemómetro digital se mide la velocidad del aire para calcular el flujo volumétrico que pasa a través de la torre y ajustar el flujo de agua para las diferentes relaciones L'/G'.
Para empezar las corridas con variación de flujo, se enciende la bomba P-2. Luego se regula el flujo de agua con la válvula V-2 y trabajar con los flujos 1.0, 0.8, 0.6, 0.4 y 0.2 gpm. Al mismo tiempo se van midiendo las temperaturas de bulbo seco y húmedo del aire a la salida de la torre, con sensores de temperatura (TS-1). Luego se realiza una perturbación en el flujo de agua con la válvula V-2 hasta llegar a estado estable con el fin de tener la repetición de los datos. Al finalizar las corridas con las repeticiones hechas se apaga el sistema y se recircula el agua utilizada que se encuentra en el tanque T-1 con la bomba sumergible P-1, para calentarla nuevamente e iniciar el ciclo una vez más a una temperatura diferente.
3. RESULTADOS Y DISCUSIÓN
Con los datos tomados de las temperaturas de bulbo seco y bulbo húmedo en la entrada y la salida de la torre de enfriamiento, se pueden determinar todas las propiedades del aire en las corridas utilizando la carta psicométrica para después calcular el coeficiente global de transferencia de masa (Kya) y otros cálculos de desempeño de la torre como el calor retirado, masa de agua evaporada y la eficiencia.
A. Cálculo del coeficiente K y a y otro indicadores de desempeño
Para el cálculo del coeficiente volumétrico de transferencia de masa (K y a) se utilizó el método de Merkel el cual se basa en una serie de asunciones para reducir la solución a un cálculo simple, una de las cuales es simplificar la transferencia de calor y masa a una diferencia de entalpia despreciando los efectos de la evaporación del agua en el proceso como se ve en la ecuación 6.
Donde,
Me M , es el número de Merkel.
L’, es el flujo másico de agua.
K ya es el coeficiente volumétrico global de transferencia de calor y masa
h yi ,h y , son las entalpias de la mezcla aire-agua en la interface y en los puntos de referencia de la torre respectivamente.
Cp w , es el calor específico del agua.
Tω, es la temperatura del agua.
Para obtener la solución de K y a se debe resolver la integral (K m ) también conocida como índice global de desempeño o número de unidades de difusión ecuación (7).
Donde:
y h y es la línea de operación que va variando con cada experimento que se realiza ya que las temperaturas de entrada y salida cambian además de la relación L'/G'. Luego obtenemos la ecuación (9) de (6) para cambiar la variable de volumen por la de longitud del
empaque. Debido a las simplificaciones del método de Merkel es necesario medir la eficiencia de la torre de enfriamiento, en la cual se tienen en cuenta el rango y la aproximación (approach). El rango es la diferencia entre la temperatura de entrada del agua a la torre y la de salida, y la aproximación es la diferencia entre la temperatura de salida del agua de la torre y la temperatura de bulbo húmedo ambiente.
La eficiencia de la torre de enfriamiento, ver ecuación (10), es la relación entre el rango de operación y rango
ideal, el cual sería la diferencia entre la temperatura del agua de entrada y la temperatura de bulbo húmedo del ambiente.
Donde,
T i ,T o , son las temperaturas de entrada y salida del agua respectivamente.
T wb , es la temperatura de bulbo húmedo del ambiente.
B. Conductividad térmica de los materiales de empaque
Los valores de la conductividad de los materiales de los empaques se presentan en la tabla 4.
Tabla 4 Conductividad térmica para cada material de empaque.
| Material | k, Conductividad térmica (W/K m) |
|---|---|
| Acrílico | 0.2 |
| Aluminio | 209.3 |
| Hierro | 80.2 |
| Madera | 0.13 |
| Vidrio | 0.8 |
El empaque de aluminio tiene un espesor de 1 mm de aluminio y en el interior del empaque hay vidrio, por lo que la conductividad térmica del empaque de aluminio se determina como una pared compuesta.
De la ecuación de Fourier para la trasferencia de calor se tiene que:
Para la pared compuesta de estudio en la Figura 5, si se considera una k del empaque R viene siendo:
Donde:

Reemplazando y despejando tenemos:
C. Análisis estadístico de resultados
Después de calcular los valores del coeficiente global de transferencia de masa ( 𝐾 𝑦 𝑎) se empleó un análisis estadístico para determinar el efecto de las variables L'/G', 𝑇 𝑤 y conductividad térmica (𝑘) del empaque frente al valor de 𝐾 𝑦 𝑎. A partir de los resultados de la literatura, se realizó una regresión lineal utilizando los logaritmos de las variables con el fin de obtener toda la información estadística pertinente del modelo. La ecuación (14) muestra la semejanza de la ecuación de Kloppers 17 en su tesis doctoral, ver ecuación (3), con la diferencia de que no se tuvo en cuenta la altura de empaque sino la conductividad del material y además las variables de flujo de aire y agua se relacionaron en una sola que es el L'/G'.
En la tabla 5 se muestra los factores trabajados junto con sus respectivos niveles. Una repetición fue hecha para un total de 200 experimentos. La tabla 6 muestra el análisis de varianza obtenido como también la ecuación de regresión (15).
Tabla 5 Factores y niveles estudiados.
| L/G | Tin, o C | K, W/m K |
|---|---|---|
| 0,2 | 40 | 0,13 |
| 0,4 | 42 | 0,2 |
| 0,6 | 44 | 0,88 |
| 0,8 | 46 | 80,2 |
| 1 | 48 | |
Tabla 6 Análisis de varianza de la regresión lineal para log ( 𝐾 𝑦 𝑎)
| Fuente | GL | SC Ajust | MC Ajust | Valor F | Valor P |
| Regresión | 3 | 1,80324 | 0,60108 | 215,08 | 0.000 |
| Log L'/G' | 1 | 1,53556 | 1,53556 | 549,45 | 0.000 |
| Log Tw | 1 | 0,02003 | 0,02003 | 7,17 | 0,008 |
| Log k o empaque | 1 | 0,24766 | 0,24766 | 88,62 | 0.000 |
| Error | 196 | 0,54776 | 0,00279 | ||
| Total | 199 | 2,35101 |
El valor P de las variables log L'/G', log 𝑇 𝑤 y log 𝑘 son inferiores a 0.05 por lo que todas tienen efecto significativo en el 𝐾 𝑦 𝑎.
La ecuación (15) es llevada a la forma de la ecuación (14) y obtenemos:
de donde se muestra que 𝐾 𝑦 𝑎 aumenta con el aumento de L'/G' y temperatura y con la disminución de la conductividad térmica del material.
A continuación, se presenta la figura 6 donde se muestra 𝐾 𝑦 𝑎 obtenido del modelo anterior contra el 𝐾 𝑦 𝑎 experimental a fin de encontrar el valor R2 y observar el ajuste. El modelo resultante presentó un R2 de 76,1 %, lo que puede atribuirse a la variabilidad de las variables flujo y temperatura.

Fuente: el autor
Figura 6 Comparación de los datos de 𝐾 𝑦 𝑎 obtenidos del modelo con los de los datos experimentales.
En la figura 7 podemos observar que la relación L/G es la que tiene mayor efecto en 𝐾 𝑦 𝑎 al igual que la conductividad térmica. Un incremento en L/G causa un incremento en 𝐾 𝑦 𝑎 mientras que la conductividad térmica (𝑘) causa un efecto inverso. La temperatura ejerce un efecto bajo, sin generar mayor impacto, disminuyendo en un sector y aumentando en el resto y esto puede deberse al fenómeno de que la temperatura de bulbo seco dentro de la torre puede estar disminuyendo y luego aumentando internamente cuando se disminuye la temperatura de entrada de agua manteniendo constante L/G algo que se debe al fenómeno de cual ejerce mayor efecto, la evaporación o la convección y que podría analizarse con el método de Mickley.
Los resultados de 𝐾 𝑦 𝑎 se relacionan con el agua evaporada, siendo necesario complementarlos con los resultados de la eficiencia obtenida para cada factor. En la tabla 7 se muestra el reporte estadístico del efecto de la temperatura, la conductividad térmica y la temperatura de entrada en la eficiencia de la torre. En ésta podemos ver que todos los factores tienen un efecto significativo, aunque el que más efecto muestra según la figura 8.a es el de la relación L/G que a medida que aumenta, disminuye la eficiencia lo que indica que es importante trabajar a altos flujos de aire o a bajos flujos de agua caliente. Esto se debe a que el aire es el que está más frio y estaría en mayor proporción causando una mayor disminución de la temperatura en el agua. Además, observamos en la figura 8.a que la temperatura de entrada a pesar de que tiene un efecto más bajo que el de L/G hace que la eficiencia aumente cuando la temperatura de entrada aumenta debido a que el gradiente de temperatura aire - agua en la torre incrementa con la temperatura de entrada causando una mayor pérdida de calor en el líquido.
Tabla 7 Análisis de varianza para la eficiencia.
| Fuente | GL | SC Ajust | MC Ajust | Valor F | Valor P |
| L/G | 4 | 16667.7 | 4166.93 | 10365.13 | 0.000 |
| Tin | 4 | 315.2 | 78.79 | 195.98 | 0.000 |
| K | 3 | 811.5 | 270.50 | 672.86 | 0.000 |
| L/G*Tin | 16 | 95.6 | 5.97 | 14.86 | 0.000 |
| L/G*K | 12 | 90.3 | 7.53 | 18.72 | 0.000 |
| Tin*K | 12 | 623.7 | 51.97 | 129.28 | 0.000 |
| L/G*Tin*K | 48 | 406.2 | 8.46 | 21.05 | 0.000 |
| Error | 100 | 40.2 | 0.40 | ||
| Total | 199 | 19050.3 |

Fuente: el autor
Figura 8 Gráfica de efectos principales para la eficiencia (a). Gráfica de interacciones para la eficiencia (b). 𝑇𝑖𝑛 (oC), 𝑘 (𝑊/𝐾𝑚)
Analizando ahora el tipo de material vemos en la figura 8.a que para mejorar la eficiencia es necesario trabajar con empaques que tengan baja conductividad térmica como lo es la madera. El uso de empaques en las torres de enfriamiento incrementa el área de transferencia de calor y masa entre los fluidos, por lo tanto, el mecanismo principal de transferencia de energía es por convección y evaporación. Sin embargo, parte del calor también es transmitido a través del empaque por conducción térmica lo que incrementa la transferencia de calor a través de este para altos valores de conductividad térmica del material. Esto causa que el calor transmitido por conducción (ver figura 9) penetre nuevamente al agua por la parte inferior en contacto con el empaque aumentando su temperatura de salida afectando el desempeño de la torre de enfriamiento. Parte del calor que el agua debería transferir a la corriente ascendente de aire por convección y evaporación, se transfiere en realidad al empaque y este a su vez al agua nuevamente. Es por esto que los rellenos de materiales con conductividad térmica elevada (hierro y aluminio) presentan una eficiencia menor que los materiales aislantes térmicos (acrílico y madera).
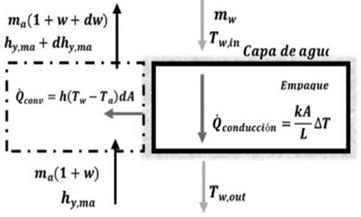
Fuente: el autor
Figura 9.Esquema de la transferencia de calor por conducción en la zona de empaque.
En la figura 8b. vemos el efecto de las interacciones de los factores en la eficiencia. Para obtener los valores más altos de eficiencia es necesario utilizar valores bajos de la relación de L/G y valores bajos de conductividad térmica K. También vemos que cuando incrementamos la temperatura de entrada junto con una disminución de L/G la eficiencia aumenta con la excepción del límite cuando L/G es 0.2 ya que la cantidad de aire que esto demanda desprecia el efecto de la temperatura de entrada.
Como resultado podemos decir que es propicio trabajar a bajos valores de L/G, con empaques de materiales con baja conductividad térmica y con altas diferencias de temperatura agua - aire.
Luego del anterior análisis, al comparar la figura 7 con la figura 8a. es necesario considerar la cantidad de agua evaporada. Si bien es importante la eficiencia, también es importante la cantidad de agua evaporada por lo que debe haber un equilibrio debido a las muchas pérdidas que se pueden obtener. Bajas valores de L/G sería lo ideal debido a que se obtiene la mayor eficiencia y la menor cantidad de agua evaporada y ayudaría aún más el trabajar con empaques con conductividad térmica alta que aun cuando tiende a disminuir la eficiencia el impacto no es tan fuerte como en la cantidad de agua evaporada.
Por último, en la tabla 8, se puede observar que el empaque tipo película tiene una eficiencia superior al tipo salpicadura hasta un 30% comparado con respecto al mismo material que fue el acrílico, debido al aumento en el área superficial (350% ) causado por el cambio de forma. Como podemos observar este empaque obtuvo el valor mayor de 𝐾 𝑦 𝑎 causando la mayor cantidad de agua evaporada y a pesar de que se obtuvo un incremento notable en la eficiencia con respecto a los demás tipos de empaque, también se obtuvo un incremento muy grande en el 𝐾 𝑦 𝑎 demostrando la importancia de hacer balances económicos que permitan saber con cuanta perdida agua se puede trabajar y así escoger el empaque adecuado.
Tabla 8 Coeficiente volumétrico global de transferencia de masa 𝐾 𝑦 𝑎 y eficiencia promedio para cada tipo de empaque.
| Tipo de empaque | k, Conductividad térmica (W/Km) | Coeficiente k y a promedio | Eficiencia promedio (%) |
|---|---|---|---|
| Acrílico (película) | 0.20 | 0,5698 | 42,81 |
| Madera (salpicadura) | 0.13 | 0,3893 | 32,99 |
| Acrílico (salpicadura) | 0.20 | 0,3503 | 29,79 |
| Aluminio (salpicadura) | 0.88 | 0,3298 | 28,48 |
| Hierro (salpicadura) | 80.2 | 0,3016 | 27,47 |
4. CONCLUSIONES
• En el presente trabajo se encontró que la relación L'/G', la conductividad térmica k, y la temperatura de entrada del líquido caliente Tin, tienen un gran efecto en el coeficiente volumétrico global de transferencia de masa 𝐾 𝑦 𝑎 el cual está directamente relacionado con la cantidad de agua evaporada. 𝐾 𝑦 𝑎 incrementa para incrementos de L'/ G', mientras que disminuye con incrementos de conductividad térmica. Por otro lado, 𝐾 𝑦 𝑎 también aumenta con incrementos en la temperatura de entrada, sin embargo, esto no sucede a temperaturas bajas.
• Conjuntamente, la eficiencia también se ve altamente afectada por los factores mencionados. Para incrementos en L'/G' la eficiencia disminuye debido a que el gas estaría en mayor proporción causando un enfriamiento rápido por transferencia de calor sensible.
• La eficiencia disminuye al poner en contacto el líquido con empaques con conductividad térmica alta como los metales tal como el hierro debido al efecto de la transmisión de calor al empaque por conducción.
• La eficiencia aumenta a medida que la temperatura de entrada aumenta debido a que el gradiente de temperatura aire - agua en la torre incrementa con la temperatura de entrada causando una mayor razón de perdida de calor en el líquido.
• Se obtuvo una correlación no lineal de k y a con respecto a la relación L'/G', la conductividad térmica k, y la temperatura de entrada del líquido caliente Ti. Esta tiene en cuenta el término de la conductividad térmica k siendo más efectiva al considerar el tipo de empaque de la torre.
• Para este tipo de análisis de torres es necesario determinar la eficiencia como también la cantidad de agua evaporada debido a las muchas pérdidas que se pueden obtener. En la interacción de los factores vemos que es recomendable trabajar a bajas relaciones de L/G con empaques con conductividad térmica alta. Este último aun cuando tiende a disminuir la eficiencia, su efecto no es tan fuerte como el que causa en la cantidad de agua evaporada.
• El aumento del área superficial de los empaques hasta un 350% puede mejorar altamente la eficiencia, pero a su vez puede hacer que se evapore mucha agua por lo que es necesario hacer balances económicos que permitan saber con cuanta perdida agua se puede trabajar y así escoger el empaque adecuado.


































