Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Eidos
Print version ISSN 1692-8857On-line version ISSN 2011-7477
Eidos no.26 Barranquilla Jan./June 2017
Chrysippus' Indemonstrables and the Semantic Mental Models*
Miguel López-Astorga
Instituto de Estudios Humanísticos "Juan Ignacio Molina".
Universidad de Talca, Chile.
milopez@utalca.cl
* This paper is a result of the Project N°. I003011, "Algoritmos adaptativos e inferencias lógicas con enunciados condicionales," supported by the Directorate for Research of the University of Talca (Dirección de Investigación de la Universidad de Talca), Chile. The author is also the main researcher of that Project.
Fecha de recepción: diciembre 23 de 2015 Fecha de aceptación: julio 1° de 2016
Resumen
Atendiendo a la lógica estándar, solo uno de los cinco indemostrables propuestos por Crisipo de Solos es realmente indemostrable. Sus otros cuatro esquemas son demostrables en tal lógica. La pregunta, por tanto, es: si cuatro de ellos no son verdaderamente indemostrables, por qué Crisipo consideró que sí lo eran. López-Astorga mostró que si ignoramos el cálculo proposicional estándar y asumimos que una teoría cognitiva contemporánea, la teoría de la lógica mental, describe correctamente el razonamiento humano, se puede entender por qué Crisipo pensó que todos sus indemostrables eran tan básicos. No obstante, en este trabajo trato de argumentar que la teoría de la lógica mental no es el único marco que puede explicar esto. En concreto, sostengo que otra importante teoría sobre el razonamiento en el presente, la teoría de los modelos mentales, también puede ofrecer una explicación al respecto.
Palabras clave: Crisipo de Solos, indemostrables, lógica mental, modelos mentales, lógica estoica.
Abstract
According to standard logic, only one of the five indemonstrables proposed by Chrysippus of Soli is actually indemonstrable. The other four schemata are demonstra-ble in that logic. The question hence is, if four of them are not really indemonstrable, why Chrysippus considered them to be so. López-Astorga showed that, if we ignore standard propositional calculus and assume that a current cognitive theory, the mental logic theory, truly describes human reasoning, it can be explained why Chrysippus thought that all of his indemonstrables were so basic. However, in this paper, I try to argue that the mental logic theory is not the only framework that can account for that. In particular, I hold that another important reasoning theory at present, the mental models theory, can offer an explanation in that regard as well.
Keywords: Chrysippus of Soli, indemonstrables, mental logic, mental models, Stoic logic.
Introduction
A s reminded by López-Astorga (2015a, pp.1-2), only one of the five ἀναπόδεικτοι (indemonstrables) that are said to be proposed by Chrysippus of Soli (Sextus Empiricus, Adversus Mathematicos 8, 223; Diogenes Laértius, VitaePhilosophorum 7, 79-81) is really an indemonstrable schema in standard propositional calculus. That schema is Modus Ponendo Ponens. The other four schemata, Modus Tollendo Ponens, Modus Ponendo Tollens I, Modus Ponendo Tollens II, and Modus Tollendo Tollens, can be demonstrated in that calculus. However, López-Astorga (2015a) claims that the only problem is the comparison of Stoic logic and standard logic, since, as stated by Bobzien (1996, p. 134) too, the former is different from the latter, and the latter hence is not the best instrument to analyze the former.
In this way, López-Astorga's (2015a) proposal is to assume a contemporary cognitive framework, the mental logic theory (see, e.g., Braine & O'Brien, 1998a; O'Brien, 2009, 2014; O'Brien & Li, 2013; O'Brien & Manfrinati, 2010). According to him, if we accept the thesis that the mental logic theory correctly describes human reasoning, it can be easily understood why Chrysippus thought that all of his ἀναπόδεικτοι were absolutely basic argu-ments. And this is so because the mental logic theory claims, as explained below, that there are certain 'Core Schemata' on the human mind that are essentially natural for all the people, and, based on them, it is not hard to check that the ἀναπόδεικτοι are to some extend linked to the deep syntax (or the basic set of formal rules) of human cognition.
But a possible challenge to López-Astorga's (2015a) account is the fact that the mental logic theory is not the only theory explai-ning the human inferential activity at present. Indeed, there are other theories, and one of them is especially strong, since there is very great experimental support for it. That is the mental models theory (e.g., Byrne & Johnson-Laird, 2009; Johnson-Laird, 2006, 2010, 2012, 2015; Khemlani, Orenes & Johnson-Laird, 2012, 2014; Oakhill & Garnham, 1996; Orenes & Johnson-Laird, 2012), a semantic framework arguing that the formal or syntactic approaches such as that of the mental logic theory do not have enough machinery to explain some experimental results that are to be found in the literature on human reasoning and that the mental models theory can account for without difficulties (very illustrative works in this regard can be, for example, Johnson-Laird, 2010, Orenes & Johnson-Laird, 2012, and López-Astorga, 2014a).
Be that as it may, the truth is that, if, instead of the mental logic theory, we assume the mental models theory, it is also possible to identify the reasons that could lead Chrysippus of Soli to con-sider the ἀναπόδεικτοι to be primary arguments that cannot be demonstrated. To show that is the main goal of this paper and I will try to achieve it by describing, firstly, what the ἀναπόδεικτοι are actually. Secondly, I will briefly explain the most important theses of the mental logic theory and how, based on them, López-Astorga argues that the indemonstrables can be considered to be really schemata or rules directly related to the human elementary mental syntax. Then, I will comment on the theses of the mental models theory relevant to the aims of this paper. And, finally, I will account for how it can also be argued that the ἀναπόδεικτοι are basic and natural from the mental models theory.
Just a few clarifications are necessary before beginning. On the one hand, perhaps using the expression 'mental models theory' can cause confusions in a study, such as this one, addressing a logical topic. I am aware of that. However, I will use that expression in this paper respecting the name that its proponents give the theory, which is exactly that. In this way, in order to avoid interpreta-tion problems, it should be taken into account that, from now on, the word 'models' will only refer to the psychological theory calling itself with it. On the other hand, as it can be checked, the words 'syntax' and 'semantic' are not being used either as they are usually in logic. In this paper, they have the senses that they have in cognitive science. So, 'syntax' has to do with relationships between and derivations from pure logical forms, and 'semantic' is linked to the idea that, when human beings make inferences, they use to pay more attention to the meanings of the concepts and expressions than to the grammatical form of the sentences. With these clarifications made, I start with a description of the indemonstrables.
Chrysippus of Soli and his ἀναπόδεικτοι
As mentioned, the ἀναπόδεικτοι assigned to Chrysippus by Dio-genes Laértius and Sextus Empiricus are five. In this section, I will review each of them in turn. To do that, I will mainly focus on the descriptions given by Diogenes Laértius (Vitae Philosophorum 7, 79-81), which are also included in fragment 9.7 proposed by Boeri and Salles (2014, pp. 216-217 and 228-229).
The first one is known as Modus Ponendo Ponens, and its de-finition (Diogenes Laértius, Vitae Philosophorum 7, 80) reveals that it is an indemonstrable ( ἀναπόδεικτος) with two premises: a conditional (συνημμένον) and the first clause of it (ἡγούμενον). Its conclusion is the second clause of the conditional (λῆγον). This is the less problematic case, since, as said, it can be stated that it is really indemonstrable in standard propositional calculus. In fact, it is a basic rule in Gentzen's (1935) system and Deaño (1999, pp. 153-155) refers to it as an original rule of propositional calculus and names it the 'conditional elimination rule.' Furthermore, it can be formally expressed in standard logic in this way:

Where '->' stands for conditional relationship (this and all of the symbols used in this paper basically match those used by López-Astorga, 2015a).
The second ἀναπόδεικτος is generally named Modus Tollendo Tollens and Diogenes' definition (VitaePhilosophorum 7, 80) shows that its two premises are a conditional (συνημμένον) and the contrary (ἀντικείμενον) of the second clause (λῆγον), and that its conclusion is the contrary (ἡγούμενον) of the first clause (riyoúnevov). Maybe this is the most controversial case, at least from a cognitive point of view. It is true that it is absolutely valid in Gentzen's (1935) calculus, but it is not a basic rule in standard logic. Nevertheless, it is not controversial for that. Its problem is that people do not always use it, and only seem to apply it in certain circumstances that, in principle, are not very obvious (see, e.g., Byrne & Johnson-Laird, 2009, pp. 282-283; López-Astorga, 2013, p. 231; López-Astorga, 2015a, pp. 8-9). In any case, its logical form is the following:
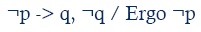
Where '¬' represents denial.
And examples of the usual derivation of [¬p] from [p -> q] and [¬q] in standard calculus are to be found in, e.g., Byrne and Johnson-Laird (2009, p. 283), López-Astorga (2013, p. 241), and López-Astorga (2015a, p. 9).
On the other hand, the third argument is usually called Modus Ponendo Tollens I, and Diogenes also explains it in Vitae Philosophorum 7, 80. He indicates that it consists of a denied (ἀποφατικός) conjunction (συμπλοκή) and one of the conjuncts as premises, and the contrary (ἀντικείμενον) of the other element as its conclusion. This argument is valid in standard logic as well. But, as Modus Tollendo Tollens, is not one of its original rules. Nevertheless, people often use it without difficulties (see, e.g., Braine & O'Brien, 1998b, p. 80). A derivation of it in standard propositional calculus can be found, for example, in López-Astorga (2015a, p. 6), and its logical form is:

Where '.' represents conjunction.
As far as the fourth indemonstrable is concerned, its name is Modus Ponendo Tollens II, it is defined by Diogenes Laértius in Vitae Philosophorum 7, 81, and has two premises: a disjunction (διεζευγμένον) and one of the disjuncts. Its conclusion is the contrary (ἀντικείμενον) of the other element. This argument is also correct in standard propositional calculus. The only inconvenience is that, as it can be noted, the disjunction is exclusive and that calculus basically deals with inclusive disjunctions. However, as it is well known and reminded by López-Astorga (2015a, p. 7), that does not mean that propositional calculus cannot address exclusive disjunctions. Initially, it can be said that the formal structure of Modus Ponendo Tollens II is as follows:

Where ' ' indicates exclusive disjunction.
' indicates exclusive disjunction.
Nonetheless, while standard propositional calculus does not use a symbol for exclusive disjunction, it is possible to transform exclusive disjunctions into formulae that can be handled by it. Thus, it can be stated that [p v q] is equivalent to

Where 'v' expresses inclusive disjunction.
In this way, standard calculus enables to draw [¬q] from [(p v q) · ¬(p · q)] and [p]. In fact, López-Astorga (2015a, p. 7) shows how this derivation could be.
Furthermore, it seems that the Stoic disjunction was essentially exclusive. As indicated, for example, by O'Toole and Jennings (2004, pp. 498-450) and, to a lesser extent, López-Astorga (2015a, p. 7), there are both secondary literature (e.g., Bocheński, 1963, p. 91; Lukasiewicz, 1967, p. 74; Mates, 1953, p. 51; Mueller, 1978, p. 16) and primary sources (e.g., Cicero, Topica 14, 56-57; Diogenes Laertius, Vitae Philosophorum 7, 72; Galen, Institutio Logica 5, 1; Gellius, Noctes Atticae 16, 8) holding this idea.
And this leads us to infer that the disjunction included in the last ἀναπόδεικτος was exclusive too. In general, it is known as Modus Tollendo Ponens, and Diogenes Laertius speaks about it in Vitae Philosophorum 7, 81 as well. He tells that its premises are a disjunction (διεζευγμένον) and the contrary (ἀντικείμενον) of one of the disjuncts, and that the conclusion is the other element. So, its logical form can be this one:

Of course, the disjunction does not need to be exclusive here. However, it seems to be more opportune to consider it to be so because of that said above: Stoic disjunction was essentially exclusive. In any case, it does not appear to be very relevant to determine exactly the type of disjunction used in this indemonstrable, since the conclusion seems obvious whether the disjunction is exclusive or inclusive. López-Astorga (2015a, p. 4) shows a derivation of it in standard propositional calculus considering it to be inclusive. Nevertheless, it is not hard to note that, if we assume that the first premise is not [p v q], but [(p v q) · ¬(p · q)], it is very easy to draw [q] from that premise and [¬p] in that calculus as well.
These are Chrysippus' indemonstrables and, as said, López-Astorga (2015a) argues that, based on the mental logic theory, the reasons why they were considered to be basic arguments by him are clear. The next section explains how López-Astorga does that.
The mental logic theory and the ἀναπόδεικτοι
As indicated, the mental logic theory holds that there are formal logical rules on the human mind that appear to be natural or innate. Nonetheless, such rules are not exactly those of standard propositional calculus. Actually, all of the rules admitted by the mental logic theory are also valid in standard logic. But the point is that not all of the rules that are valid in this later logic are ad-mitted by the mental logic theory. The theory only accepts the schemata with enough empirical support. In this way, it can be said that it is an experimental approach and that it only takes into account the logical schemata that, following empirical results in experiments, individuals truly apply.
On the other hand, not all of the schemata have the same status in the theory. In fact, it distinguishes different types of rules. However, only two of them are important for the goals of this paper: 'Core Schemata' and 'Feeder Schemata.' The Core Schemata "are used without restriction whenever they are applicable" (Braine & O'Brien, 1998b, pp. 79-83). The Feeder Schemata in turn "are used only when their output feeds another schema or the evaluation of a conclusion" (Braine & O'Brien, 1998b, p. 83).
Based on all of this, according to López-Astorga (2015a), it is not difficult to account for the reasons why Chrysippus understood that his five arguments were indemonstrable. As explained, four of them are not so in standard propositional calculus. Nevertheless, if we assess them from the mental logic theory, the situation is very different. Firstly, it can be stated that three of the ἀναπόδεικτοι match three Core Schemata, which clearly means that they can be thought to be parts of the basic syntactic or formal structure of human reasoning. Those three indemonstrables are Modus Ponendo Ponens, Modus Tollendo Ponens, and Modus Ponendo Tollens I.
Indeed, López-Astorga (2015a, p. 3) claims that Modus Ponendo Ponens is Schema 7 of the theory, a Core Schema that is expressed in Braine and O'Brien (1998b, p. 80, table 6.1) in a way akin to this one:

Secondly, Modus Tollendo Ponens can be related to Schema 3 of the mental logic theory (López-Astorga, 2015a, p. 5), another Core Schema that in Braine and O'Brien (1998b, p. 80, Table 6.1) has a form similar to the following:

As far as Modus Ponendo Tollens I ¡s concerned, something similar can be said. According to López-Astorga (2015a, p. 6) it corresponds to Schema 4 of the theory. That is another Core Schema and Braine and O'Brien (1998b, p. 80, table 6.1) presents a structure akin to this one:

The problems hence seem to be provided by Modus Ponendo TollensIIand Modus Tollendo Tollens. Nonetheless, as said, López-Astorga (2015a) also gives arguments based on the mental logic theory to explain why Chrysippus of Soli could include them into the indemonstrables set.
His solution for the problem that the disjunction is exclusive in Modus Ponendo Tollens II is essentially the same as that indicated in the previous section from standard logic. True, although, in the mental logic theory, disjunction is inclusive too, it can deal with exclusive disjunctions in the same way as propositional calculus. Following the theory, it is not hard to accept that [(p  q) = (p v q) · ¬(p · q)] (López-Astorga, 2015a, p. 8). Likewise, it is also clear that the mental logic theory enables to derive [¬q] from [(p v q) · ¬(p · q)] and [p]. The reasons, according to López-Astorga (2015a, p. 8) are Modus Ponendo Tollens I(i.e., Schema 4) and Schema 9 (a Feeder Schema) in Braine and O'Brien (1998b, p. 80, table 6.1). This later schema has a formal structure similar to the following:
q) = (p v q) · ¬(p · q)] (López-Astorga, 2015a, p. 8). Likewise, it is also clear that the mental logic theory enables to derive [¬q] from [(p v q) · ¬(p · q)] and [p]. The reasons, according to López-Astorga (2015a, p. 8) are Modus Ponendo Tollens I(i.e., Schema 4) and Schema 9 (a Feeder Schema) in Braine and O'Brien (1998b, p. 80, table 6.1). This later schema has a formal structure similar to the following:

And it hence allows deducing [¬(p · q)] from [(p v q) · ¬(p · q)]. In this way, Modus Ponendo Tollens I, or, if preferred, Schema 4, in turn enables, as indicated, to derive [¬q] from [¬(p · q)] and [p]. So, this ἀναπόδεικτος is not a problem for the theory either.
Finally, López-Astorga (2015a, pp. 8-12) offers an account of Modus Tollendo Tollens too. In principle, this indemonstrable can be problematic because is not a schema of any kind (for example, Core or Feeder) in the mental logic theory. Therefore, it seems that it is difficult for the theory to explain not only the fact that individuals apply it only in some cases, and not always, but also the fact that Chrysippus assumed it as an indemonstrable. However, López-Astorga (2015a, p. 9) thinks that, despite this, the theory does be able to solve these problems. In his view, it is absolutely evident in passages such as that of Diogenes Laértius at Vitae Philosophorum 7, 73 that Chrysippus did not understand the conditional in the same way as standard logic. According to Chrysippus, a real συνημμένον is not so just by including the word εi (if). It is also necessary a certain relationship between the clauses. In particular, the contrary (ἀντικείμενον) of the second clause (λῆγον).) must be inconsistent with (μάχεται) the first clause (ἡγούμενον). López-Astorga bases his explanation on arguments such as those that are to be found in O'Toole and Jennings (2004, p. 492). Nevertheless, what is important here is that, in López-Astorga's view, this means that Chrysippus' logic, or Stoic logic, held that, in a sentence with the form [p -> q], the contents of [p] and [q] have to be clearly related. And they need to be so to the extent that, given [p -> q], people can easily and quickly note that it implies [¬q -> ¬p] as well. Thus, the idea is that individuals only use Modus Tollendo Tollens when the conditional is an actual conditional, i.e., when [p -> q] leads, by virtue of its content, to [¬q -> -p]. When this happens, the derivation of [¬p] from [p -> q] and [¬q] is very simple, since, given that to accept as a premise [p -> q] is at the same time to assume as another premise [¬q -> -p], the deduction of [¬p] is just an application of Modus Ponendo Ponens to the formulae [¬q -> -p] and [¬q] (López-Astorga, 2015a, p. 10). In this way, it is not hard to understand why, despite its cognitive problems, Chrysippus of Soli thought that Modus Tollen-do Tollens was a basic argument. It was so because the argument referred to a conditional, and conditionals needed to fulfill a special requirement in Stoic logic. Thus, when that requirement was fulfilled, Modus Tollendo Tollens was always applied.
But the most important goal of this paper is to show that, while this account of the five ἀναπόδεικτοι given by López-Astorga from the mental logic theory appears to be absolutely right, as said, it is also possible to offer an explanation of them based on the mental models theory. The mental logic theory is able to ex-plain why Chrysippus claimed that his arguments were basic and indemonstrable (although, as indicated, four of them are actually demonstrable in standard propositional calculus). However, the mental models theory can do that too. I will argue in this direction in the following pages. I begin commenting on the main theses of the mental models theory related to the indemonstrables.
The mental models theory and the logical operators
The models theory is different from the mental logic theory. While the latter is formal and syntactic, the former is semantic and content-based (comparisons between the two theories are to be found, for example, in López-Astorga, 2014b, 2015b, 2015c), with the meanings that such concepts have in cognitive science field and the current studies on reasoning. In this way, the mental models theory claims that the human mind works analyzing the possibilities that can be attributed to sentences. Of course, those possibilities are considered to be semantic, and it can be said that the theory interprets them as something similar to iconic models, in the sense that the philosopher Peirce gives to the word 'iconic' (Johnson-Laird, 2012, p. 136). Thus, the theory assigns certain models to each operator in classical logic, and the basic idea is that individuals make inferences reviewing the models of the premises, accepting only those that are consistent with the models of the other premises, and rejecting those that are contradictory with those same models.
However, a very interesting point of this theory is that people do not always note all the models corresponding to a particular proposition. The proponents of the theory distinguish between 'Mental Models' and 'Fully Explicit Models' (see, e.g., Johnson-Laird, 2012, p. 138, table 9.2). The Mental Models are the models that can be identified easily and without effort. On the other hand, the Fully Explicit Models are usually hard to detect, unless (and, as shown below, this is important for this paper) the semantic content, the meaning, or pragmatic factors make them explicit.
For the aims of this paper, only some cases are relevant: that of the conditional, that of conjunction, that of the exclusive dis-junction, and that of the denial. The rest of this section reviews those cases in turn.
According to Johnson-Laird (2012, p. 138, table 9.2), a conditional such as 'If A, then B' has only one Mental Model in the theory. That Mental Model is as follows:
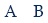
This model refers to a situation in which both the antecedent and the consequent (A and B respectively) are true. Nevertheless, a conditional really allows two more possibilities, which, along with the previous Mental Model, are the elements of the entire Fully Explicit Models set. Thus, as indicated by Johnson-Laird (2012, p. 138, table 9.2), the Fully Explicit Models of the condi-tional are the following:

As it can be noted, in the second model the antecedent is false and the consequent is true, and in the third model both of them are false.
But the case of conjunction is different. The mental models theory provides that an expression of the type 'A and B' only has a Mental Model, which matches its only element in its Fully Explicit Models set. That Mental Model and only element in the Fully Explicit Models set of conjunction is, according to Johnson-Laird, 2012, p. 138, table 9.2), this one:
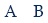
As far as the exclusive disjunction is concerned, i.e., as far as an expression such as 'A or else B but not both' is concerned, the Mental Models given by Johnson-Laird (2012, p. 138, table

And the Fully Explicit Models shown by him in that same place are:

Finally, in connection with the denial of an expression, it can be said that the theory considers its models to be the complement of the set of the models of that same expression when it is affirmed (see, e.g., Khemlani et al., 2012, pp. 646-678). For example, if, as indicated, conjunction has only one model, the denial of a con-junction will be linked to the other three possible combinations, that is, to these scenarios:

These theses of the mental models theory are enough to achieve the goals of this paper and to show that this later theory can also explain why Chrysippus thought that his ἀναπόδεικτοι were so essential. However, maybe it is appropriate to say that the theory is much broader too. For instance, it deals with biconditionals and inclusive disjunctions as well. Nevertheless, neither its account of biconditionals nor its explanation of inclusive disjunctions needs to be taken into account here. On the one hand, it is obvious that no ἀναπόδεικτος refers to the biconditional. On the other hand, although it can be thought that the account of the inclusive dis-junction can be necessary in the case of Modus Tollendo Ponens, as argued, disjunction was clearly exclusive in Stoic logic, and the models that the mental models theory attributes to the exclusive disjunction can, as explained below, describe the inference made in the cases of both Modus Tollendo Ponens and Modus Ponendo Tollens II.
Furthermore, a very curious datum that, in my view, deser-ves to be highlighted is that the mental models theory seems to confirm the Stoic thesis that disjunction is mainly exclusive. In fact, a prediction of the theory is that individuals tend to interpret affirmative disjunctions as exclusive, and Khemlani et al. (2014, p. 4, Table 1) showed that this prediction is correct. In the first experiment of their paper, they used sentences such as this one:
"Bob [asserted/ denied] that he wore a yellow shirt [and/or] he wore blue pants on Monday" (Khemlani et al., 2014, p. 4).
Obviously, the contents in square brackets referred to different experimental conditions, but the condition that is relevant for the issue of the exclusive disjunction is, undoubtedly, that in which the content of the first square brackets was 'asserted' and that of the second square brackets was 'or.' Participants' task consisted of, given the previous sentence, indicating which of the following possibilities were adequate:
"Bob wore a yellow shirt and he wore blue pants.
Bob wore a yellow shirt and he wore non-blue pants.
Bob wore a non-yellow shirt and he wore blue pants.
Bob wore a non-yellow shirt and he wore non-blue pants"
(Khemlani et al., 2014, p. 4).
The result was that, in the case of the disjunction, a significant number of participants only selected the second option ('Bob wore a yellow shirt and he wore non-blue pants') and the third one ('Bob wore a non-yellow shirt and he wore blue pants'), which, as it can be noted, means that, because those options match the models corresponding to the exclusive disjunction, they tended to consider disjunction to be exclusive.
Therefore, I think that it is absolutely justified to take into account only the models that the theory assigns to the exclusive disjunction. That is the sense that the Stoics appear to have given to disjunction and, in addition, the sense that, according to the mental models theory, people seem to tend to give it in a natural way (irrespective the fact that, as stated, the models set corres-ponding to the inclusive disjunction is not necessary to explain the reasons that lead Chrysippus to propose his ἀναπόδεικτοι).
But, as indicated, only two of the indemonstrables refer to dis-junction. Other two of them are related to the conditional, and one more of them includes a denied conjunction. We hence need to consider the description above in entirety (which refers not only to the exclusive disjunction, but also to the conditional and the negated conjunction) to explain the reasons why Chrysippus of Soli claimed that his arguments were indemonstrable. I do this later task in the next section.
The mental models theory and the ἀναπόδεικτοι
That Modus Ponendo Ponens is really basic is easy to check from the mental models theory. It is only required individuals to identify the Mental Model of the first premise (i.e., the conditional) to note that, in a scenario in which [p -> q] and [p] are true, only [q] can be true, and [¬q] is not possible. Indeed, that Mental Model would be as follows:

Evidently, the model clearly reveals that [q] happens when [p] also happens. Nevertheless, nothing changes if, for any reason, individuals detect all of the Fully Explicit Models, since, in that case, the only option would continue to be that [q] is true. True, such Fully Explicit Models would be the following:

And, as it can be checked, the only scenario in which the se-cond premise [p] is true continues to be the first one, which is a scenario in which [q] is true too. So, Modus Ponendo Ponens seems to be absolutely natural on the human mind following the mental models theory as well.
Modus Tollendo Ponens is not a problem for the framework of the mental models theory either. Its first premise is a disjunction (which, as said, should be considered to be exclusive) and, although, in principle, its Mental Models do not enable to derive the conclusion (remember that those Mental Models, in the case of a sentence such as [p  q], would be just [p] and just [q], that the second premise is [¬p], and that the conclusion is [q]), a very little effort can lead one to the Fully Explicit Models and to draw the conclusion. The key seems to be the presence of [¬p] as the second premise. That presence easily reveals that the possible scenarios are not simply [p] alone or [q] alone, but these ones:
q], would be just [p] and just [q], that the second premise is [¬p], and that the conclusion is [q]), a very little effort can lead one to the Fully Explicit Models and to draw the conclusion. The key seems to be the presence of [¬p] as the second premise. That presence easily reveals that the possible scenarios are not simply [p] alone or [q] alone, but these ones:

Thus, given that the second premise eliminates the first model (p is true in it), the only possibility if [p  q] and [¬p] are true is that [q] is true as well.
q] and [¬p] are true is that [q] is true as well.
The case of Modus Ponendo Tollens I is even easier to explain from the mental models theory. The first premise is now a denied conjunction such as [¬(p · q)], which means that its models are:

Because the second premise is [p], it is clear that the second and the third models must be removed (they describe scenarios in which [p] is not true). Therefore, it is only possible the first situation, i.e., a situation in which [q] is false.
And, given that we have assumed, following the mental models theory, that human beings tend to interpret disjunctions as exclusive, Modus Ponendo Tollens II is not hard to account for either. Again, the Mental Models are not enough and it is necessary to identify the Fully Explicit Models to draw [¬q] from [p  q] and [p]. However, it can be thought that this is also something very simple here and that it does not require a lot of cognitive effort. The Mental Models of the first premise are:
q] and [p]. However, it can be thought that this is also something very simple here and that it does not require a lot of cognitive effort. The Mental Models of the first premise are:

Nonetheless, the second premise [p] eliminates the second mo-del, and that same action reveals immediately that, in a scenario in which [p] is true, [q] cannot also be so, i.e., it shows that the real possibilities are:

And, since the second one has been removed, the only addi-tional datum is that, if [p] is true, [q] is not.
Finally, it can be said that not even Modus Tollendo Tollens is hard to explain from the mental models theory. In fact, as it can be checked in the literature on this framework (e.g., Byrne & Johnson-Laird, 2009, pp. 282-283; López-Astorga, 2013, p. 235), the theory has enough machinery to account for why Modus Tollendo Tollens is only applied in certain occasions. The reason is obvious. To use Modus Tollendo Tollens it is absolutely necessary to detect the Fully Explicit Models of a conditional such as [p -> q], i.e., these models:

And this is so because, if only the Mental Model (i.e., as indi-cated, the first element of the previous set of models) is detected, it is not possible to derive [¬p] from [p -> q] and [¬q]. Indeed, the third one of the Fully Explicit Models of the conditional (the model in which both [p] and [q] are false) is the only model in which [q] is not true, and, therefore, if it is not identified, individuals cannot see what happens in a scenario in which [¬q] is true (that is, that [¬p] is also true).
But all of this allows understanding why, in spite of its difficul-ties, Chrysippus of Soli included Modus Tollendo Tollens into the set of his ἀναπόδεικτοι. However, to clearly realize that, as in the case of the account given by López-Astorga from the mental logic theory, it is necessary to resort to Chrysippus' interpretation of the συνημμένον. That interpretation is important because can even reveal, as indicated above, that the Stoics noted, as the proponents of the mental models theory centuries later, that their form does not determine conditionals and that their semantic content is decisive when we reflect on them. In any case, as stated, in Chry-sippus' view, an actual conditional is that in which it is obvious that the contrary (ἀντικείμενον) of the consequent (λῆγον) and the antecedent (ἡγούμενον) are not possible at the same time. So, Chrysippus' συνημμένον is a conditional that enables individuals to note the possibility to which the third Fully Explicit Model refers in an easy, simple, and quick way.
To Chrysippus, a sentence such as, for instance, 'if I go to your home, I eat fish' is not a real conditional, since not to eat fish is not in conflict with to go to your home. Nevertheless, an example given by Diogenes Laértius (Vitae Philosophorum 7, 80), which López-Astorga (2015, pp. 9-10) also refers to, is very enlightening. That example is:
εἰ ἡμέρα ἐστί, φῶς ἐστιν ('if it is daytime, there is sunlight')
Evidently, this does be a real conditional since it is not possible that there is no sunlight and it is daytime at the same time. Thus, it can be thought that what Chrysippus meant is that Modus To-llendo Tollens is not appropriate to a sentence such as the first one (i.e., that of your home and fish), which is not an actual conditional, but only to sentences such as the second one (i.e., that of the daytime and sunlight). But, if this is so and we assume that the mental models theory really describes human reasoning, the reasons that led Chrysippus to propose Modus Tollendo Tollens as an indemonstrable are clear.
While the Fully Explicit Models of the first sentence (according to Chrysippus' view, the false conditional) are difficult to identify, those of the second one (according to Chrysippus' view, the true conditional) require less cognitive effort to be noted. Therefore, it can be said that Chrysippus considered Modus Tollendo Tollens to be one of his indemonstrables because he thought that it had to be applied to a very particular kind of sentence. A kind that does not exactly match what we consider to be a conditional today, but a kind with the word eí (if) fiilfilling the special requirement of showing, by virtue of its content and the meaning of its clau-ses, that the only possibility if the consequent if false is that the antecedent is false too.
In this way, it is relevant to emphasize that semantic (remember that this concept only refers to the meaning of the words) is a crucial element of the mental models theory. As said, the content and the meanings of the sentences can lead models to be made explicit. In addition, it is particularly interesting that the theory proposes even certain mechanisms of modulation that can modify the initial models of a sentence (see, e.g., Orenes & Johnson-Laird, 2012, pp. 357-377). It hence can account for the fact that Chrysippus of Soli claimed that Modus Tollendo Tollens was a basic and indemonstrable argument. He referred to an argument whose first premise was not a conditional such as we interpret that type of sentence, but a συνημμένον with a content with the capacity to make explicit all of the possible scenarios (or, if preferred, models) to which it refers. From this point of view, it can even be argued that, at least in a sense, Stoic logic was an anticipation of the mental models theory, since, as said, the Stoics noted that the logical form is not necessarily the most relevant element in an inference.
Conclusions
It is beyond discussion that, if we accept that the mental logic theory correctly describes human inferential activity, it is abso-lutely obvious why Chrysippus of Soli thought that his five argu-ments were indemonstrable. The point of this paper is that it shows that, if, on the contrary, we assume the mental models theory, the reasons that could lead him to consider his ἀναπόδεικτοι to be so basic and essential are very clear as well.
Thus, given that these two theories are very representative and relevant at present, it can be claimed that, although that was not necessarily his intention, Chrysippus managed to some extent to describe the actual way reasoning really works. So, from this point of view, it does not seem to be opportune to speak about Stoic logic as a simple anticipation of standard propositional logic.
In this way, it can be thought that another interesting fact is that Stoic logic, the mental logic theory, and the mental models theory are three frameworks different from standard logic that share their capacity to explain which the most basic inferences that can be made by human beings are. It is evident that such inferences do not match Gentzen's (1935) most elementary rules. Therefore, while certain correspondences and parallels between the three mentioned approaches and standard logic can be found, it can be stated that, if something is clear, it is that this later logic actually describes neither human reasoning nor the most essential processes of thought.
Furthermore, although there is no doubt that Stoic logic needs to be interpreted and understood in its own context, it can be said that, if was an anticipation of any framework, that can be the mental logic theory or the mental models theory, but not, as indicated, standard propositional logic. However, as far as this issue is concerned, it appears that the relationships between Stoic logic and the mental models theory are more evident than those between the former and the mental logic theory. And this is so for three reasons. Firstly, as shown, Stoic logic and the mental models theory share the interpretation of disjunction as exclusive. Secondly, there are also other works explaining particular aspects of the Stoic logic by means of the theoretical resources of the mental models theory. For example, in López-Astorga (2016), it is shown that the first of the Stoic θέματα (reduction rules) could be accepted by virtue of semantic processes as well, and that it is not necessarily the result of a syntactic deduction process. Thirdly, as also indicated, the mental models theory, unlike the mental logic theory, does not need formulae or syntactic schemata akin to those of standard propositional calculus to account for reasoning, and this is more like Stoic logic, which does not appear to resort to pure logical forms either. It hence can be thought that the Stoic view of inference was more semantic than syntactic (in the sense that the mental models theory gives to these words), although perhaps this problem requires further research.
References
Bobzien, S. (1996). Stoic syllogistic. In C. C. W. Taylor (Ed.), Oxford Studies in Ancient Philosophy (pp. 133-192). Oxford, UK: Clarendon Press. [ Links ]
Bocheński, I. M. (1963). Ancient Formal Logic. Amsterdam, The Netherlands: North-Holland. [ Links ]
Boeri, M. D. & Salles, R. (2014). Los filósofos estoicos. Ontología, lógica, física y ética. Santiago de Chile, Chile: Ediciones Universidad Alberto Hurtado. [ Links ]
Braine, M. D. S. & O'Brien, D. P. (Eds.) (1998a). Mental Logic. Mahwah, NJ: Lawrence Erlbaum Associates Publishers. [ Links ]
Braine, M. D. S. & O'Brien, D. P. (1998b). The theory of mental-propositional logic: Description and illustration. In M. D. S. Braine & D. P. O'Brien (Eds.), Mental Logic (pp. 79-89). Mahwah, NJ: Lawrence Erlbaum Associates Publishers. [ Links ]
Byrne, R. M. J. & Johnson-Laird, P. N. (2009). "If" and the problems of conditional reasoning. Trends in Cognitive Science, 13(7), 282-287. [ Links ]
Deaño, A. (1999). Introducción a la lógica formal. Madrid, Spain: Alianza Editorial. [ Links ]
Gentzen, G. (1935). Untersuchungen über das logische Schlieften I. MathematischeZeitschrift, 39, 176-210. [ Links ]
Johnson-Laird, P. N. (2006). How We Reason. Oxford, UK: Oxford University Press. [ Links ]
Johnson-Laird, P. N. (2010). Against logical form. Psychologica Belgica, 5(3/4), 193-221. [ Links ]
Johnson-Laird, P. N. (2012). Inference with mental models. In K. J. Holyoak & R. G. Morrison (Eds.), The OxfordHandbook of Thinking and Reasoning (pp. 134-145). New York, NY: Oxford University Press. [ Links ]
Johnson-Laird, P. N. (2015). How to improve thinking. In R. Wegerif, L. Li & J. C. Kaufrnan (Eds.), The Routledge International Handbook of Research on Teaching Thinking (pp. 80-91). Abingdon, UK, & New York, NY: Routledge. [ Links ]
Khemlani, S., Orenes, I. & Johnson-Laird, P. N. (2012). Negation: A theory of its meaning, representation, and inference. Psychological Review, 109(4), 646-678. [ Links ]
Khemlani, S., Orenes, I. & Johnson-Laird, P. N. (2014). The negation of conjunctions, conditionals, and disjunctions. Acta Psychologica, 151, 1-7. [ Links ]
López-Astorga, M. (2013). Are conditional and disjunction really comparable? Universum, 28(2), 229-242. [ Links ]
López-Astorga, M. (2014a). The conditional introduction rule and human reasoning: Findings from the mental models theory. Cogency, 5(2), 29-37. [ Links ]
López-Astorga, M. (2014b). The mental logic theory and DeMorgan's laws. International Journal of Humanities and Social Science, 4(11-1), 24-28. [ Links ]
López-Astorga, M. (2015a). Chrysippus' indemonstrables and mental logic. Croatian Journal of Philosophy, 15(43), 1-15. [ Links ]
López-Astorga, M. (2015b). Reductio adabsurdum, modulation, and logical forms. International Journal of Philosophy and Theology, 3(1), 59-65. [ Links ]
López-Astorga, M. (2015c). The formal discipline theory and mental logic. Praxis Filosófica, 41, 11-25. [ Links ]
López-Astorga, M. (2016). The first rule of Stoic logic and its relationship with the indemonstrables. Tópicos. Revista de Filosofía, 50, 9-23. [ Links ]
Lukasiewicz, J. (1967). On the history of the logic of propositions. In S. McCall (Ed.), Polish Logic: 1920-1939 (pp. 67-87). Oxford, UK: Clarendon Press. [ Links ]
Mates, B. (1953). Stoic Logic. Berkeley and Los Angeles, CA: University of California Press. [ Links ]
Mueller, I. (1978). An introduction to Stoic logic. In J. M. Rist (Ed.), The Stoics (pp. 1-26). Berkeley, CA: University of California Press. [ Links ]
Oakhill, J. & Garnham, A. (Eds.) (1996). Mental Models in Cognitive Science. Essays in Honour of Phil Johnson-Laird. Hove, UK: Psychology Press. [ Links ]
O'Brien, D. P. (2009). Human reasoning includes a mental logic. Beha-vioral and Brain Sciences, 32, 96-97. [ Links ]
O'Brien, D. P. (2014). Conditionals and disjunctions in mental-logic theory: A response to Liu and Chou (2012) and to López-Astorga (2013). Universum, 29(2), 221-235. [ Links ]
O'Brien, D. P. & Li, S. (2013). Mental logic theory: A paradigmatic case of empirical research on the language of thought and inferential role semantics. Journal of Foreign Languages, 36(6), 27-41. [ Links ]
O'Brien, D. P. & Manfrinati, A. (2010). The mental logic theory of conditional proposition. In M. Oaksford & N. Chater (Eds.), Cognition and conditionals: Probability and Logic in Human Thinking (pp. 39-54). Oxford, UK: Oxford University Press. [ Links ]
Orenes, I. & Johnson-Laird, P. N. (2012). Logic, models, and paradoxical inferences. Mind & Language, 27(4), 357-377. [ Links ]
O'Toole, R. R. & Jennings, R. E. (2004). The Megarians and the Stoics. In M. D. Gabbay & J. Woods (Eds.), Handbook of theHistory of Logic, Volume I. Greek, Indian and Arabic Logic (pp. 397-522). Amsterdam, The Netherlands: Elsevier. [ Links ]














