Francisco Jaime Mejía*

* Ingeniero Civil, Univeridad Nacional de Colombia. Profesor de Hidráulica, Escuela de Ingeniería de Antioquia, Colombia. Grupo de Investigación Espiral.pffmejia@eia.edu.co

Artículo recibido 19-V-2008. Aprobado 21-VII-2008

Discusión abierta hasta diciembre de 2008

Uno de los objetivos de un curso básico de hidráulica del flujo libre en canales es el análisis de perfiles del flujo gradualmente variado. Este trabajo proporciona una estrategia de enseñanza-aprendizaje que puede mejorar la práctica universitaria docente de la hidráulica. Es bien conocida la gráfica profundidad contra energía específica (y-E) para describir e interpretar la hidráulica del flujo libre. Se propone complementarla con la gráfica profundidad contra pendiente de energía (y-sf). A partir de las comparaciones gráficas se ilustran los conceptos de flujo subcrítico (y>ycrítica, v<vcrítica), crítico y supercrítico de un lado, y de otro, los conceptos de flujo subnormal (y>ynormal, v<vnormal), normal y supernormal, y se explica por este camino el comportamiento de los doce posibles perfiles de flujo gradualmente variado.

One objective of an introductory course of open-channel flow is the analysis of gradually varied flow profiles. This paper shows a teaching-learning strategy that might improve the university practices for teaching hydraulics. It is well known the depth-specific energy curve (y-E) for describing and interpreting open-channel flow hydraulics. It is proposed to complement that curve with the depth-energy slope curve (y-sf). By using a graphic comparison, it aims to illustrate the concepts of the subcritical (y>ycritical, v<vcritical), critical and supercritical flow concepts and, on the other hand, the subnormal (y>ynormal, v<vnormal), normal y supernormal flow concepts. This way, it is proposed to explain the behavior of the twelve possible gradually varied flow profiles.

Se presentan las relaciones analíticas y, especialmente, la gráfica de la profundidad y la energía específica por una parte y, por otra, la gráfica de profundidad contra pendiente de fricción. En cada caso se muestran las ramas de flujo subcrítico y supercrítico en la primera y, en la segunda, de flujo subnormal y supernormal, después se relacionan entre sí y se pasa a mostrar la ubicación de los diferentes perfiles de flujo gradualmente variado en cada gráfica. El propósito que se busca es facilitar la comprensión de estas relaciones entre quienes se inician en el estudio de la hidráulica.

ENERGÍA ESPECÍFICA EN CANALES

La expresión para la energía en una sección respecto a un nivel de referencia que pasa por el fondo del canal se conoce como energía específica (Bakhmeteff, 1912, citado por Chow, 1959) y se escribe así:

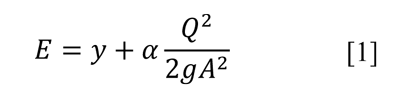
La curva y-E se muestra en la figura 1, donde también aparecen destacadas la profundidad crítica asociada con la energía mínima y las ramas que representan los flujos subcrítico (SbC) y supercrítico (SpC) a partir del punto C sobre la curva. En esta gráfica no interviene la pendiente del fondo del canal.

PENDIENTE DE FRICCIÓN EN CANALES

La expresión para la pendiente de fricción en canales se obtiene con la ecuación de Manning (ec. 2a) (Chow, 1959) o con la ecuación de Darcy-Weisbach (ec. 2b) (French, 1985). El factor de fricción de Darcy se calcula con la ecuación de Colebrook-White (ec. 3), cuando el flujo es turbulento (Dyhouse et al., 2003), o con la ecuación de Poiseuille (ec. 4) cuando es eliminar. El número de reynolds se calcula con la ecuación 5. La ecuación dos se puede trasformar (Mejia,2008) para calcular la profundidad de la pendiente del fondo del canal (ec. 6) y obtener la profundidad normal.

La figura 2 muestra la variación de la pendiente de fricción con la profundidad. Allí se destaca la profundidad normal asociada con la pendiente del fondo del canal y las ramas que representan el flujo subnormal (SbN) y el supernormal (SpN). El punto N sobre la curva indica dónde empiezan las ramas.

RELACIÓN ENTRE LA CURVA DE ENERGÍA ESPECÍFICA Y LA CURVA DE PENDIENTE DE FRICCIÓN

Cuando la profundidad crítica se usa para calcular la pendiente de fricción (ec. 2), se obtiene la pendiente crítica del canal, que siempre es positiva (Sc>0). Gráficamente esta relación se ilustra en la figura 3, donde se han acoplado las dos gráficas de interés para poner de manifiesto tal relación.

RELACIÓN ENTRE LA CURVA DE PENDIENTE DE FRICCIÓN Y LA CURVA DE ENERGÍA ESPECÍFICA

Con la ecuación 6 se puede obtener la profundidad normal a partir de la pendiente del fondo del canal en aquellos canales con pendiente de fondo positiva (So>0). Esta profundidad puede resultar mayor o menor que la profundidad crítica. En el primer caso se obtiene un flujo normal subcrítico, y en el segundo se está ante un flujo normal supercrítico. Gráficamente esta relación se ilustra con la figura 4, donde se han acoplado las dos gráficas de interés para poner de manifiesto tal relación.

LAS ZONAS DE FLUJO EN LA SECCIÓN DE UN CANAL

Las profundidades normal y crítica dividen la curva de pendiente de fricción en tres segmentos. La curva de energía específica se divide también en tres segmentos con esas dos profundidades. En cualquiera de las dos curvas, el segmento que representa las profundidades de flujo mayores que las dos profundidades de referencia corresponde a la zona 1 de flujo en la sección. El segmento que representa las profundidades comprendidas entre las dos profundidades de interés corresponde a la zona 2 de flujo. Por último, el segmento que representa las profundidades de flujo inferiores a las dos profundidades tratadas corresponde a la zona 3 de flujo. La figura 5 representa gráficamente estas zonas de flujo en la curva de pendiente de fricción y la figura 6 representa las zonas de flujo en la curva de energía específica.

LA CURVA DE PENDIENTE DE FRICCIÓN Y LA CLASIFICACIÓN DE LOS CANALES SEGÚN LA PENDIENTE

Desde el punto de vista de la pendiente, los canales se clasifican como canales de pendiente adversa (A, So<0), de pendiente horizontal (H, So=0) o de pendiente sostenida (So>0). En los canales tipo A y H se considera que la profundidad normal, que se calcula con la ecuación 6, es un valor infinito o tiende a él. Así que en estos canales no existe la zona 1 de flujo.

Los canales de pendiente sostenida, a su vez, se clasifican como canales de pendiente moderada (M, 0<So<Sc, figura 7), canales de pendiente crítica (C, 0<So=Sc, figura 8) y canales de pendiente escarpada (S, 0<Sc<So, figura 9).

La representación de los valores relativos de las profundidades normal y crítica sobre la curva de pendiente de fricción es un elemento de análisis e interpretación del flujo variado que permite a quienes se inician en el estudio de la hidráulica la comprensión de las características del flujo que puede ocurrir a diversas profundidades de flujo en diferentes tipos de canal. Las profundidades normal y crítica se pueden llevar a la curva de energía específica. Las dos curvas quedan divididas en tres segmentos. El segmento superior de ambas curvas representa flujo subnormal y subcrítico, el segmento inferior representa flujo supernormal y supercrítico, el segmento intermedio representa flujo supernormal- subcrítico (canal M) o subnormal-supercrítico (canal S). Tanto en la curva de energía como en la de pendiente de fricción se pueden representar las tres zonas de flujo en canales de pendiente sostenida. Estas zonas se corresponden mutuamente en las dos gráficas. En cualquier tipo de canal aparecerán allí representados los tres perfiles de flujo que aparecen en los canales de pendiente positiva. También aparecen representadas las dos zonas de flujo en los canales de pendientes adversa y horizontal. En la medida que se comprende mejor este comportamiento, el análisis de otras situaciones relacionadas puede ser más inmediato, más profundo y más útil.

La nomenclatura usada en este documento es la siguiente:

A área de la sección

c subíndice que denota una variable en estado crítico

D profundidad hidráulica

E energía específica

f factor de fricción de la ecuación de Darcy-Weissbach

g aceleración gravitacional

k_s rugosidad equivalente de arena

n coeficiente de rugosidad de Manning n subíndice que denota una variable en flujo normal

R radio hidráulico

R_e número de Reynolds

S_bC flujo subcrítico

S_bN flujo subnormal

S_c pendiente crítica

S_f pendiente de la línea de energía

So pendiente del fondo del canal

S^pC flujo supercrítico

S^pN flujo supernormal

y profundidad de flujo

α coeficiente de corrección de Coriolis

μ viscosidad absoluta

ρ densidad

Chow, Ven Te (1959). Open Channel Hydraulics. McGraw- Hill. New York, New York.        [ Links ]

Dyhouse, Gary R.; Hatchett, Jennifer; and Benn, Jeremy (2003). Floodplain modeling using HEC-RAS. 1st ed. Haested Press, Waterbury, CT. http://www.haestad.com/library/books/FMRAS/floodplainonlinebook/javascript/wwhelp/wwhimpl/java/html/wwhelp.htm        [ Links ]

French, Richard, H. (1985). Open-channel hydraulics. McGraw-Hill. New York, New York.        [ Links ]

Mejía Garcés, Francisco Jaime (2008). Mecánica de fluidos y recursos hidráulicos. Escuela de Ingeniería de Antioquia, http://fluidos.eia.edu.co, consultado el 31 de marzo de 2008, 325 Mb.        [ Links ]