Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.12 Envigado July/Dec. 2009
REGRESIÓN Y CORRELACIÓN DE SUPERFICIES ÓPTICAS DE REVOLUCIÓN EN FORMA CANÓNICA CONOCIDOS LOS RADIOS DE CURVATURA
REGRESSION AND CORRELATION OF OPTICAL SURFACES OF REVOLUTION IN CANONICAL FORM KNOWN THE RADII OF CURVATURE
REGRESSÃO E CORRELAÇÃO DE SUPERFÍCIES ÓPTICAS DE REVOLUÇÃO EM FORMA CANÔNICA CONHECIDOS OS RÁDIOS DE CURVATURA
Juan Camilo Valencia*,Álvaro Hernán Bedoya**
* Ingeniero de Producción y Magíster en Matemáticas Aplicadas, Universidad EAFIT. Profesor Asistente, Escuela de Ingeniería de Antioquia. Medellín, Colombia. jucava@eia.edu.co
** Licenciado en Matemáticas y Física, Universidad de Antioquia. Magíster en Matemáticas Aplicadas, Universidad EAFIT. Profesor, Institución Educativa Manuel José Sierra. Girardota, Antioquia, Colombia. rigelbach@hotmail.com
Artículo recibido 27-I-2009. Aprobado 14-XII-2009
Discusión abierta hasta junio de 2010
RESUMEN
Se presentan tres modelos matemáticos para la regresión y correlación de una nube de N puntos en R3 con coordenadas cartesianas xj, yj como abscisas, con su respectiva ordenada ri como radio de curvatura de la sección axial o sagital, pero que no corresponde a la curvatura gaussiana, con un paraboloide, elipsoide e hiperboloide de revolución en forma canónica. Este modelo acepta que los datos están debidamente centrados, es decir, el vértice de las superficies de revolución está preestablecido en el origen, por lo cual es aplicable a la córnea humana.
PALABRAS CLAVE: córnea; correlación; elipsoide; hiperboloide; queratometría; paraboloide; regresión; topógrafo corneal.
ABSTRACT
Three mathematical models are presented for the regression and correlation of a cloud of N points in R3 with Cartesian coordinates xj, yj as abscissas, with his respective ordinate ri as a radius of curvature of the axial or sagittal section, but not corresponding to the Gaussian curvature, with a paraboloid, ellipsoid, and hyperboloid of revolution in canonical form. This model assumes that data are properly centered, that is, the apex of the surfaces of revolution is preset at the origin; therefore, it is applied in human cornea.
KEY WORDS: cornea; correlation; ellipsoid; hyperboloid; keratometry; paraboloid; regression; corneal topographer.
RESUMO
Apresentam-se três modelos matemáticos para a regressão e correlação de uma nuvem de N pontos em R3 com coordenadas cartesianas xj, yj como abscissas, com sua respectiva ordenada ri como rádio de curvatura da seção axial ou sagital, mas que não corresponde à curvatura gaussiana, com um paraboloide, elipsoide e hiperboloide de revolução em forma canônica. Este modelo supõe que os dados estão devidamente centrados, isto é, o vértice das superfícies de revolução está preestabelecido na origem; pelo qual é aplicavel à córnea humana.
PALAVRAS CÓDIGO: córnea; correlação; elipsoide; hiperboloide; queratometria; paraboloide; regressão; topógrafo corneano.
1. INTRODUCCIÓN
El primer modelo que se desarrolla en el presente documento es útil en particular para el control de calidad de la geometría de una superficie especular con sección parabólica, como en espejos para telescopios, o para verificar superficies ópticas que resultan de los procesos de spin-casting para lentes de contacto (Wichterle y Wichterle, 1970) y espejos líquidos con fluidos en rotación libre (Angel et al. 2008). También este modelo puede usarse para hacer un análisis de regresión y correlación de la córnea humana con un paraboloide de revolución con la información suministrada por los queratómetros computarizados.
El segundo modelo es útil para el control de calidad de la geometría de una superficie especular con sección elíptica que se aplana hacia la periferia, como en espejos para instrumentos, o para verificar superficies ópticas que resultan de los procesos de torneado de lentes CNC. También este modelo puede usarse para hacer un análisis de regresión y correlación de la córnea humana (Davis et al., 2005) con un oblate elipsoide de revolución con la información suministrada por los queratómetros computarizados. Es importante mencionar que las superficies elípticas tienen reflexión perfecta de foco a foco y también presentan refracción perfecta en el foco más lejano al vértice, si los rayos son paraxiales, por lo tanto, son ideales para modelar córneas, si se supone visión lejana. Adicionalmente, también se incluye el modelo de regresión y correlación de un prolate elipsoide de revolución en forma canónica, útil para verificar la superficie corneal post-keratomileusis in situ (Huang, Shekhar y Tang, 2003), a pesar de que no presente refracción perfecta.
Y el tercer modelo es útil para el control de calidad de la geometría de una superficie especular con sección hiperbólica como en espejos para instrumentos, o para verificar superficies ópticas que resultan de los procesos de torneado de lentes CNC. También este modelo puede emplearse para hacer un análisis de regresión y correlación de la córnea humana con un hiperboloide de revolución con la información suministrada por los queratómetros computarizados. Conviene mencionar que las superficies hiperbólicas tienen reflexión perfecta de foco real a foco virtual y también presentan refracción perfecta paraxial para los rayos que provienen de un foco cercano, por lo cual son aplicables para modelar córneas si se supone visión cercana, en especial en casos de alta miopía corneal comunes a todos los queratoconos.
Los métodos de regresión y correlación de sistemas no lineales se resuelven usualmente mediante dos técnicas:
La primera técnica usa un algoritmo (Bates y Watts, 1988) que permite iterativamente aproximar los valores de los parámetros desconocidos, obteniendo un estimado lineal para sus cambios (Valencia y Bedoya, 2009).
La segunda técnica usa un algoritmo directo que permite resolver sistemas de ecuaciones no lineales en varias variables de forma iterativa mediante el uso de herramientas de cómputo. Esta técnica es la que se recomienda para el uso práctico de este trabajo (Ortega y Rheinboldt, 2000), lo cual no es objeto de este estudio.
2. REGRESIÓN Y CORRELACIÓN DE UN PARABOLOIDE DE REVOLUCIÓN
Para la verificación de la calidad de una superficie óptica correspondiente a un paraboloide de revolución se usan instrumentos modernos como topógrafos computarizados, microscopios y nanoscopios, queratómetros computarizados que permiten generar una imagen bidimensional con zonas de nivel o tridimensional con superficies de nivel que caracterizan la superficie. Algunos de estos instrumentos generan las elevaciones métricas en un sistema de coordenadas cilíndricas (r, θ, z); existen muchos instrumentos que suministran la información de la superficie con un sistema de coordenadas experto que incluye la curvatura (r, θ, k) o, en su lugar, radios de curvatura (x, y, ρ) en coordenadas cartesianas. A continuación se muestra un sistema equivalente que permite unificar los tres sistemas de medición usando como modelo (x, y, ρ). La figura 1 muestra la imagen que resulta de la medición de la superficie anterior de la córnea humana de un paciente en particular.
Se observa en la figura 1 la queratometría que muestra las zonas isocurvatura con curvas de nivel en colores o con puntos que tienen la misma curvatura. Por norma internacional, se acepta que la información presentada por estos instrumentos permite calcular los radios de curvatura ρ como función de la curvatura k, en milímetros, equivalentes para cada pixel a

donde 1,3375 es equivalente al índice de refracción del sistema simplificado córnea-humor acuoso de Le Grand. Algunos fabricantes de estos instrumentos adoptan como índice de refracción 1,3376.
Los métodos de regresión han sido ampliamente usados como algoritmos de análisis numérico y estadístico para determinar la geometría que mejor se adapta a los datos correspondientes a una nube puntos en R2 o en R3 con una función matemática preestablecida, que en este caso particular corresponde a un paraboloide de revolución en coordenadas cilíndricas

para determinar la distancia focal ƒa que mejor se ajusta a los datos suministrados por el instrumento de medición.
2.1 Método de los mínimos cuadrados con las ordenadas
Para hacer la regresión de la imagen topográfica de una nube con N puntos de la forma (xj, yj, ρj) con eje centrado, se reduce el problema a R2 con

así, la nube de N puntos toma la forma (rj, ρj) para efectuar la regresión por el método de los mínimos cuadrados en R2 con un error total de la forma

Explícitamente la geometría de la superficie que corresponde al paraboloide de revolución puede ser expresada con

Así, también los radios de curvatura principales del paraboloide de revolución se calculan con

Para cada punto de la topografía (rj, ρj), se determina la ordenada correspondiente z mediante las soluciones reales de

la cual es

donde Sgn (ƒa) corresponde al signo de la distancia focal para indicar el sentido del paraboloide con relación al eje z. Si se supone el signo positivo por simplicidad, los valores obtenidos para zj serán siempre positivos, ya que el mínimo radio de curvatura en el vértice es el doble de la distancia focal.
Sustituyendo (8) con el signo positivo en (4) se obtiene

Para minimizar el error total Et se deriva (9) con relación a la variable desconocida ƒa:
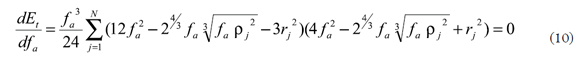
Simplificando y expandiendo (10) se obtiene

con  donde la solución real y más positiva para la ecuación (11) puede ser obtenida por métodos numéricos, usando modelos matemáticos estándares (Kincard y Cheney, 1994).
donde la solución real y más positiva para la ecuación (11) puede ser obtenida por métodos numéricos, usando modelos matemáticos estándares (Kincard y Cheney, 1994).
2.2 Método de los mínimos cuadrados con las curvaturas de la córnea humana
Este método alterno permite minimizar el error total como función de las curvaturas,
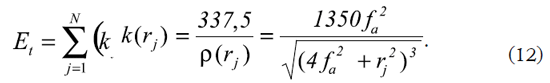
donde
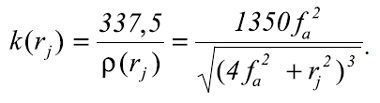
Minimizando el error total

Así, la solución para ƒa puede obtenerse con métodos numéricos. Es importante considerar que este método hace énfasis en la zona central de la córnea, ya que es más curva en el centro y se aplana hacia la periferia, por lo tanto, puede dar mejores resultados prácticos y clínicos para ƒa que los obtenidos con (11).
Es más conveniente usar para la regresión y correlación corneal el método de los mínimos cuadrados con las curvaturas que con los radios de curvatura, ya que en la periferia los radios de curvatura son muy grandes y el modelo haría énfasis en la zona periférica, que por lo general no tiene mucho interés óptico, debido a que la mayoría de la luz que ingresa al ojo es central.
2.3 Índice de correlación
Como es usual para las regresiones con líneas curvas, se define el índice de correlación cc como un número adimensional entre cero y uno, para indicar la bondad del ajuste. Así,

reemplazando (8) definida positiva en (14) y la función del paraboloide

con la distancia focal ƒa obtenida en la regresión.
3. REGRESIÓN Y CORRELACIÓN DE UN ELIPSOIDE DE REVOLUCIÓN
En este caso, la geometría de la regresión corresponde a un elipsoide de revolución en coordenadas cilíndricas con vértice en el origen definido por
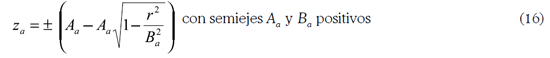
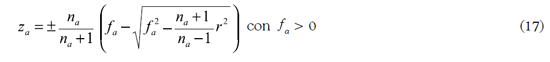
donde na es el índice de refracción de una lente o de la córnea humana con un valor de 1,376 a 555 nm, si se considera refracción perfecta en la segunda superficie corneal, pero si se adopta el modelo simplificado na = 1,3375, para determinar los semiejes o la distancia focal ƒa que mejor se ajusta a los datos suministrados por el instrumento de medición. Para facilitar la comprensión del lector se supondrá el signo positivo en las ordenadas del elipsoide de ahora en adelante.
La figura 2 muestra otra imagen que resulta de la medición de la superficie anterior de la córnea humana de un paciente en particular usando otro instrumento.
3.1 Regresión de un oblate elipsoide
La nube de N puntos toma la forma (rj, ρj), para efectuar la regresión por el método de los mínimos cuadrados en R2 con un error total de la forma
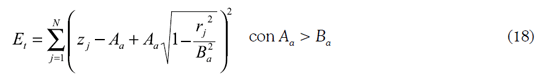
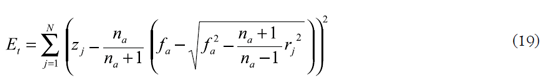
para las funciones (16) y (17) respectivamente. Se observa claramente que la regresión debe calcular los dos semiejes usando (18), o si se desea, se supone la superficie con refracción perfecta para calcular sólo la distancia focal ƒa usando (19).
Explícitamente la geometría de la superficie que corresponde al elipsoide de revolución puede expresarse con

o respectivamente

Así, también los radios de curvatura principales del elipsoide de revolución se calculan con
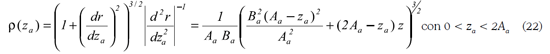
o respectivamente
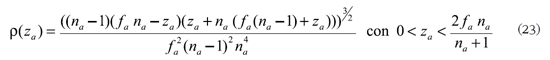
para calcular 
Para cada punto de la topografía (rj, ρj ), se determina la ordenada correspondiente zj mediante la solución real de
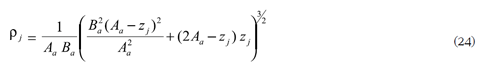
con la solución

o respectivamente si se supone refracción perfecta
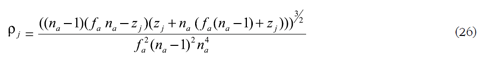
que corresponde a
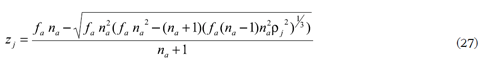
Substituyendo (25) o (27) en (18) o (19) respectivamente y simplificando para calcular
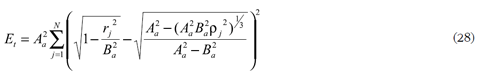
y desarrollando

o si se supone refracción perfecta
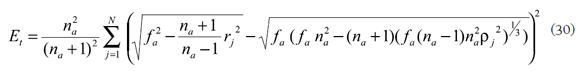
y desarrollando

Para minimizar el error total Et se derivan (28) y (30) con relación a las variables desconocidas Aa, Ba o ƒa , según el criterio de diseño sin refracción perfecta central o con ella. Como los sumandos no son funciones lineales de las variables desconocidas, se hace necesario el uso de un método numérico con la linealización de los kernels o sin ella, usando series de Taylor alrededor del origen, pero recordando que los desarrollos generan errores considerables cuando se alejan del origen, por eso es importante considerar el mayor número de términos que sea posible.
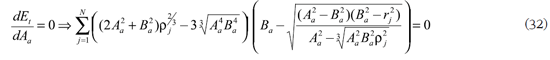
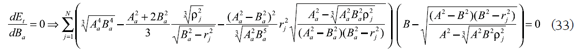
para construir un sistema de dos ecuaciones con incógnitas Aa y Ba.
Y si se supone refracción perfecta
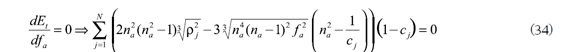
con
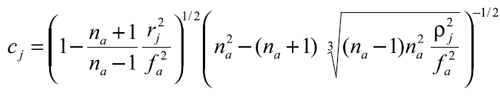
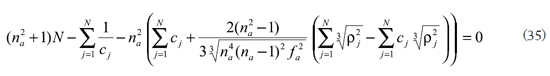
para determinar con métodos numéricos la distancia focal ƒa.
Aceptando que la córnea humana se ajusta para visión lejana, con el modelo simplificado córnea-humor acuoso na = 1,3375, la expresión anterior se reduce a


Y si se acepta refracción perfecta en la interfase córnea-humor acuoso na = 1,376:

con

3.2 Regresión de un prolate elipsoide
En este caso no se aplica la refracción perfecta central. Usando el mismo procedimiento utilizado para la regresión de un oblate elipsoide de revolución con coordenadas cilíndricas, en forma canónica za = ± (Ba – Ba √1-r2 /Aa 2) con Aa > Ba, la solución final es equivalente a (32) y (33) pero con el intercambio de semiejes Aa y Ba, así:
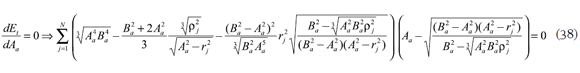

para construir un sistema de dos ecuaciones con incógnitas Aa y Ba.
3.3 Regresión de una esfera
Como caso especial, si los semiejes de la elipse son iguales, el sistema degenera en el caso esférico donde el radio Aa de la esfera que mejor se ajusta a la nube de puntos satisface

donde la solución real no negativa para Aa puede obtenerse con métodos numéricos.
3.4 Regresión de un oblate elipsoide usando el método de los mínimos cuadrados con las curvaturas de la córnea humana
Este método alterno permite minimizar el error total como función de las curvaturas,
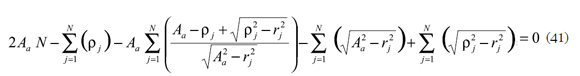
Minimizando el error total

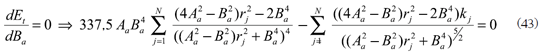
Que pueden ser sumadas para obtener una expresión más simple

Así, las soluciones para Aa y Ba pueden obtenerse con métodos numéricos.
Si se supone refracción perfecta

y si na =1,3375

y si na =1,376

con ƒa y rj en milímetros.
Es importante considerar que este método hace énfasis en la zona central de la córnea, puesto que es más curva en el centro y se aplana hacia la periferia, por consiguiente, puede dar mejores resultados prácticos y clínicos para Aa y Ba, o ƒa que los obtenidos con (32) y (33), o (34), a pesar de que el índice de correlación sea más bajo.
3.5 Índice de correlación
Reemplazando (25) en (14) y la función del elipsoide
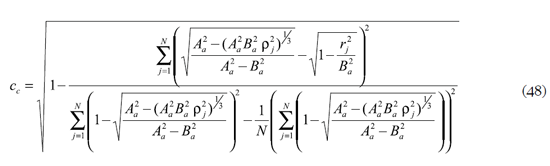
con las constantes Aa y Ba obtenidas en la regresión.
Suponiendo refracción perfecta, el índice de correlación cc se obtiene al reemplazar (27) en (14) y la función elipsoide con refracción perfecta, así:
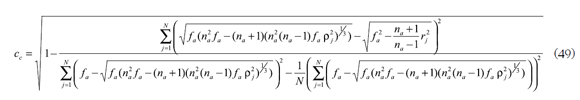
con la distancia focal ƒa obtenida en la regresión.
El índice de correlación para el sistema simplificado córnea-humor acuoso de Le Grand con na =1,3375 es:

El índice de correlación para la interfase aire-córnea para uso en un modelo con refracción perfecta en la superficie posterior con na =1,376 es:
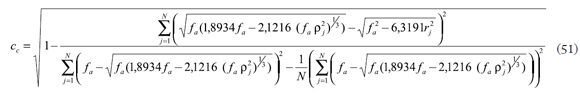
con la distancia focal ƒaobtenida en la regresión.
La figura 3 muestra la imagen que resulta de la medición de la superficie anterior de la córnea humana de un paciente en particular.
4. REGRESIÓN Y CORRELACIÓN DE UN HIPERBOLOIDE DE REVOLUCIÓN
En este caso corresponde a un hiperboloide de revolución en coordenadas cilíndricas con vértice en el origen definido con


donde na es el índice de refracción de una lente o de la córnea humana con un valor de 1,376 a 555 nm, si se considera refracción perfecta en la segunda superficie corneal, pero si se adopta el modelo simplificado na = 1,3375; y así, determinar los semiejes o la distancia focal ƒa que mejor se ajusta a los datos suministrados por el instrumento de medición. Al igual que en el elipsoide, para facilitar la comprensión del lector, se supondrá el signo positivo en las ordenadas.
4.1 Regresión de un hiperboloide En este caso el error total es

o
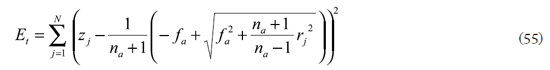
para las funciones (52) y (53) respectivamente. Se observa con claridad que la regresión debe calcular los dos semiejes usando (54), o si se desea, se supone la superficie con refracción perfecta para calcular sólo la distancia focal ƒa usando (55).
Explícitamente la geometría de la superficie que corresponde al hiperboloide de revolución puede expresarse con

o respectivamente
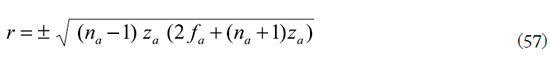
Así, también los radios de curvatura principales del hiperboloide de revolución se calculan con

o respectivamente
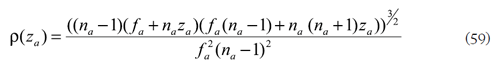
para calcular

Para cada punto de la topografía (rj, ρj), se determina la ordenada correspondiente z mediante la solucione real de
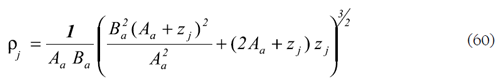
que corresponde a

o respectivamente si se acepta refracción perfecta

que corresponde a

Sustituyendo (61) o (63) en (54) o (55) respectivamente y simplificando para calcular el error total como función de los radios de curvatura se tiene

y desarrollando
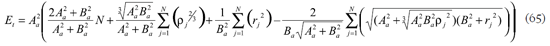
si se supone refracción perfecta

y desarrollando
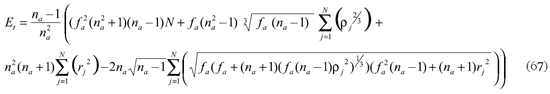
Para minimizar el error total Et se derivan (64) y (66) con relación a las variables desconocidas Aa, Ba o ƒa, según el criterio de diseño sin refracción perfecta central o con ella.
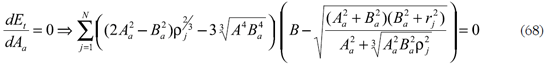
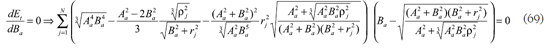
para construir un sistema de dos ecuaciones con incógnitas Aa y Ba.
Y si se supone refracción perfecta

con 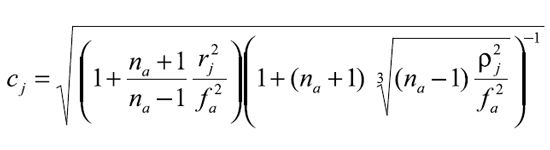 cuyo desarrollo se reduce a
cuyo desarrollo se reduce a
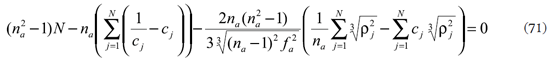
para determinar con métodos numéricos la distancia focal ƒa.
4.2 Regresión de un hiperboloide usando el método de los mínimos cuadrados con las curvaturas de la córnea humana
Este método alterno permite minimizar el error total como función de las curvaturas,

donde 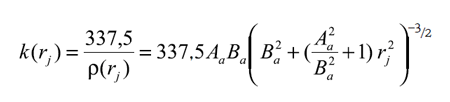
Minimizando el error total
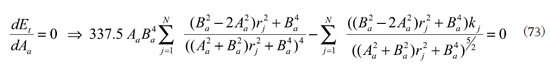
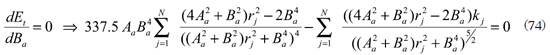
Que se pueden sumar para obtener una expresión más simple
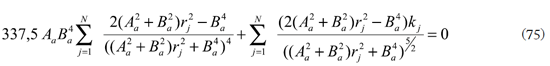
Así, las soluciones para Aa y Ba pueden obtenerse con métodos numéricos.
Si se supone refracción perfecta

y si na =1,3375 para el sistema simplificado córnea-humor acuoso de Le Grand
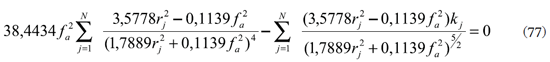
y si na =1,376 para la interfase aire-córnea para usarse en un modelo con refracción perfecta en la superficie posterior
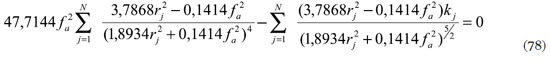
con ƒa y rj en milímetros.
Se debe aclarar que, aunque histológicamente la córnea humana tiene diferentes tipos de células con diferentes índices de refracción, el estroma corneal es el tejido más abundante, que prácticamente configura el índice de refracción promedio nc = 1,376; sin embargo, debe recordarse que las células epiteliales de la primera y delgada superficie tienen un índice de refracción de 1,401. Los modelos matemáticos que se desarrollen en el futuro posiblemente considerarán estos detalles. Algunos sistemas láser con pulsos de femtosegundos (10-12 s) usados para la keratomileusis in situ aprovechan las diferencias ópticas que existen entre las diversas capas de células corneales para iniciar la cirugía desepitelizando la córnea, creando un alerón de células epiteliales con la membrana de Bowman y así exponer el estroma a la ablación (remoción de tejido por evaporación), sin los riesgos comunes que implica el uso del microqueratomo2 (Carriazo-Barraquer, 2001) con anillo de fijación.
4.3 Índice de correlación
Reemplazando (61) en (14) y la función del hiperboloide
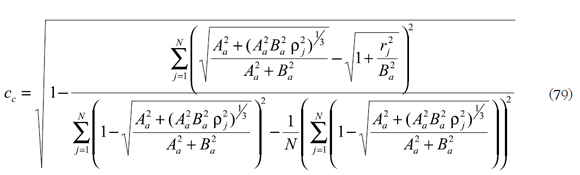
con las constantes Aa y Ba obtenidas en la regresión.
Si se supone refracción perfecta, el índice de correlación cc se obtiene al reemplazar (63) en (14) y la función elipsoide con refracción perfecta, así:

con la distancia focal fα obtenida en la regresión.
El índice de correlación para el sistema simplificado córnea-humor acuoso de Le Grand con nα =1,3375 es:

El índice de correlación para la interfase aire-córnea para su utilización en un modelo con refracción perfecta en la superficie posterior con nc = 1,376 es:

5. CONCLUSIONES
El modelo matemático-estadístico presentado permite modelar con precisión y exactitud, de forma automática, lentes para instrumentos, espejos, lentes de contacto, lentes intraoculares y cirugías refractivas, utilizando la información pixelada a color medida por los modernos queratómetros computarizados con el futuro desarrollo de software experto. El modelo también sirve para su uso en oftalmoingeniería en técnicas de “eye tracking” (localización automática del punto focal de visión) y para el desarrollo de lentes personalizados.
Nomenclatura
A Variable recurrente
Aα Semieje mayor anterior
B Variable recurrente
Bα Semieje menor anterior
C Variable recurrente
cc Coeficiente o índice de correlación
cj Variable j-ésima recurrente
D Variable recurrente
Et Error total
fα Distancia focal geométrica u óptica anterior
j Punto j
K Poder queratométrico corneal
k Curvatura o queratometría
kj Queratometría j-ésima
N Número de puntos
nα Índice de refracción relativo al aire
r Radio polar
rj Radio polar j-ésimo
x Abscisa cartesiana
xj Abscisa j-ésima cartesiana
y Abscisa cartesiana
yj Abscisa j-ésima cartesiana
z Ordenada cilíndrica
zα Ordenada cartesiana anterior
zj Ordenada j-ésima cartesiana
θ Ángulo polar
ρ Radio de curvatura
ρj Radio de curvatura j-ésimo
REFERENCIAS
1. Angel, Roger; Worden, Simon P.; Borra, Ermanno F.; Eisenstein, Daniel J.; Foing, Bernard; Hickson, Paul; Josset Jean-Luc; Ma, Ki Bui; Seddiki, Omar, Sivanandam1, Suresh; Thibault, Simon and Van Susante, Paul. A cryogenic liquid-mirror telescope on the moon to study the early universe. 2008. ApJ680 1582-1594. The Astrophysical Journal. American Astronomical Society. [ Links ]
2. Bates, Douglas M. and Watts, Donald G. Nonlinear regression and its applications. New York: John Wiley, 1988. [ Links ]
3. Carriazo-Barraquer. US Patent 6,302,896 octubre 16 de 2001. [ Links ]
4. Davis, William R.; Raasch, Thomas W.; Mitchell, G Lynn; Mutti, Donald O. and Zadnik, Karla. Corneal asphericity and apical curvature in children: a cross-sectional and longitudinal evaluation. College of Optometry, The Ohio State University, Columbus, Ohio. Investigative Ophthalmology and Visual Science. 2005; 46:1899-1906.DOI: 10.1167/iovs.04-0558. [ Links ]
5. Huang, David; Shekhar, Raj and Tang, Maolong. Method and apparatus for controlling ablation in refractive surgery. Patente WO/2003/075778, Aplicacion Internacional No.: PCT/US2003/006343 18.09.2003 Applicate: The Cleveland Clinic Foundation. Cleveland, OH. [ Links ]
6. Kincaid, David y Cheney, Ward. Análisis numérico: las matemáticas del cálculo científico, Addison- -Wesley Iberoamericana, 1994. [ Links ]
7. Ortega, James M. and Rheinboldt, Werner C. Iterative solution of nonlinear equations in several variables. Classics in Applied Mathematics. Philadelphia: SIAM, 2000. ISBN 0-89871-461-3. [ Links ]
8. Valencia, Juan Camilo y Bedoya, Álvaro Hernán. Regresión y correlación de la superficie anterior de la córnea humana con toroide regular de revolución, Revista Ingeniería y Ciencia, Universidad EAFIT, 2010, en proceso de publicación. [ Links ]
9. Wichterle, Kamil and Wichterle, Otto. Surface shapes of fluids in rotating vessels. Czech. Academy of Sciences. Prague, Czechoslovakia. Applied Scientific Research 22. April 1970. [ Links ]














