Carlos Alberto Castro*, Diana Cecilia Uribe**

^* Ingeniero de Producción, Universidad Eafit; MsC. Ingeniería industrial, Universidad de los Andes. Profesor Asociado, Departamento de Ingenieria de Producción, Universidad Eafit. Medellín, Colombia. ccastro@eafit.edu.co

^** Ingeniera de Producción, Universidad Eafit; Especialista en Gerencia de la Producción y el Servicio, Escuela de Ingeniería de Antioquia. Profesora Asistente, Ingeniería Industrial, Escuela de Ingeniería de Antioquia. Medellín, Colombia. pfdianauribe@eia.edu.co

Artículo recibido 14-IX-2010. Aprobado 7-XII-2010

Discusión abierta hasta junio de 2011

Los modelos de series de tiempo son técnicas cuantitativas con frecuencia utilizadas para realizar pronósticos de variables, dentro de los cuales se encuentran los modelos de suavización, en particular el de suavización con ajuste de tendencia, llamado también modelo de Holt, que requiere la definición de los parámetros a y b y conocidos como coeficientes de suavización y de los valores de inicio que son fundamentales para su actualización. En este artículo se propone una forma de obtener estos valores mediante la optimización del rango de la señal de rastreo (TSR) que permitan lograr un modelo más confiable desde el punto de vista de la exactitud de los resultados y de su desempeño histórico. Se realizan algunas comparaciones con modelos propuestos que utilizan la desviación absoluta media (MAD) y el error cuadrado medio (MSE) las cuales son las medidas tradicionalmente utilizadas para determinar el grado de exactitud de un modelo, lográndose obtener un comportamiento mejor de modelo.

Time series models are quantitative techniques commonly used to forecast the behavior of variables. These models include the exponential smoothing with trend or Holt model that requires the definition of the smoothing constants α and β and the initialization values, both required for the model upgrade. This paper proposes a different way to obtain the parameter values and initial conditions of the Holts model, optimizing the tracking signal range (TSR), in order to achieve a more robust model from the viewpoint of accuracy of the results and historical performance. Some comparisons between the proposed approach and the traditional methods based on the mean absolute deviation (MAD) and the mean square error (MSE) are provided. These are the measures traditionally used to determine the degree of accuracy of a model, and a better model performance is obtained.

Os modelos de séries de tempo são técnicas quantitativas frequentemente utilizadas para realizar prognósticos de variáveis, dentro dos quais se encontram os modelos de suavização, em particular o modelo de suavização com ajuste de tendência, chamado também modelo de Holt, que requer a definição dos parâmetros α e β conhecidos como coeficientes de suavização e dos valores de início que são fundamentais para a sua atualização. Neste artigo propõe-se uma forma de obter estes valores mediante a otimização do alcance do sinal de rastreio (TSR) que permitam conseguir um modelo mais confiável desde o ponto de vista da exatidão dos resultados e do seu desempenho histórico. Realizam-se algumas comparações com modelos propostos que utilizam o desvio absoluto médio (MAD) e o erro quadrado médio (MSE) as quais são as medidas tradicionalmente utilizadas para determinar o grau de exatidão de um modelo, conseguindo-se obter um comportamento melhor de modelo.

Los modelos de suavización exponencial se encuentran clasificados dentro de las técnicas cuantitativas de proyección, que hacen parte del análisis de series de tiempo. De acuerdo con varios estudios realizados (Gardner, 1985, 2006; De Gooijer y Hyndman, 2006; Syntetos, Boylan y Disney, 2009), estos modelos son utilizados ampliamente en las empresas para gestión y la administración de la demanda por medio de la cadena de abastecimiento, debido ante todo a su robustez y a que han mostrado un desempeño igual o superior en comparación con otros más sofisticados (Makridakis, Wheelwright y Hyndman, 1998; Gelper, Fried y Croux, 2010).

Por otra parte, existen en el mercado una gran cantidad de softwares desarrollados para realizar pronósticos, pero son muy pocos los que logran ser catalogados como sistemas de previsión que ofrecen el estado del tema en cuanto a funcionalidad, ya que la mayoría incluyen métodos muy simples, que no optimizan los parámetros y utilizan métodos ingenuos de inicio en los modelos de suavización y, en algunos casos, presentan errores en los cálculos, entre muchos otros problemas (Küster, McCullough y Bell, 2006), siendo estas algunas causas que, sumadas a los altos costos de varias de estas herramientas, han llevado a las empresas a tener bajos niveles de satisfacción y a usarlas muy poco, como en el caso de Colombia (Rey, 2008). Por el contrario, la utilización de hojas electrónicas de cálculo se ha convertido en la herramienta más común para desarrollar, encontrar sus parámetros y analizar modelos de series de tiempo, debido a su flexibilidad, fácil uso y bajo costo (Sanders y Manrodt, 2003).

El uso de hojas electrónicas para el desarrollo de muchas de las etapas de los procesos de planeación de producción y operaciones (incluidos los modelos de series de tiempo) se ha convertido en el común denominador dentro de los cursos de administración de operaciones (Castro, 2008; Heizer y Render, 2009), así como la utilización de la herramienta Solver de Excel para optimizar los parámetros en los modelos de suavización exponencial (Billah et al., 2006).

Los dos principales problemas relacionados con los modelos de suavización, concretamente con el de Holt, son: (1) la necesidad de especificar los parámetros α y β utilizados en el modelo, los cuales, en la mayoría de las oportunidades, son definidos subjetivamente por el usuario final basado en su experiencia y (2) la forma de definir los valores de inicio del modelo, la cual utiliza heurísticas muy simples basadas en algunos datos históricos.

Para enfrentar el problema de la subjetividad en la selección de parámetros α y β, se han realizado algunas investigaciones (Billah et al., 2006; Gelper, Fried y Croux, 2010) que muestran cómo encontrarlos optimizando alguna de las medidas de desempeño de los pronósticos como la desviación absoluta media (MAD), el error cuadrado medio (MSE) o el error medio (ME). Por su parte Rasmussen (2004) propone en su artículo la obtención tanto de los parámetros α y β del modelo, como la de los valores de inicio, definiendo para ello el MSE como función objetivo por minimizar y resolviendo el modelo de optimización con Solver.

En este artículo se demuestra que al definir como función objetivo el rango de la señal de rastreo para encontrar los valores de los parámetros α y β y los valores de inicio del modelo de Holt, se obtiene un modelo de pronósticos más robusto en su desempeño histórico, lo cual se puede visualizar por medio de la señal de rastreo, en comparación con los resultados obtenidos en investigaciones previas en donde la función objetivo definida es minimizar el MSE o el MAD del modelo de pronósticos.

En el caso de que haya en los datos históricos patrones con tendencia y se desee emplear el análisis de series de tiempo para realizar proyecciones, existen varios modelos que pueden ser utilizados, dentro de los cuales se encuentra el modelo de suavización exponencial con ajuste de tendencia o de Holt (Holt, 1957). De acuerdo con este modelo, los pronósticos en el tiempo t (F₁t) para el período t+m se hacen por medio de la expresión:

El valor S_t representa la proyección de la porción estable de la serie de tiempo y se actualiza con la expresión:

El valor D_t-1 representa la demanda del período precedente.

El valor Tt representa el ajuste por tendencia que se le hace al modelo y se actualiza con:

Los parámetros α y β, también llamados coeficientes de suavización, están restringidos a valores entre 0 y 1. Por otra parte, los modelos de suavización, en general, requieren supuestos en los valores de inicio para comenzar el proceso de cálculo y realizar las proyecciones. En el modelo Holt se requiere definir los valores iniciales de S_t y T_t los cuales en muchas aplicaciones se especifican por defecto de una forma sencilla por medio de las siguientes fórmulas:

Con el fin de medir la exactitud de los modelos de series de tiempo, se usa, por lo regular, la desviación absoluta media (MAD) o el error cuadrado medio (MSE), que se calculan a partir de las fórmulas (6) y (7) respectivamente:

Mediante estas medidas de desempeño se calcula un único valor que agrega la magnitud de las desviaciones de los errores del pronóstico y son, para la mayoría de los autores, la función objetivo que se busca minimizar. Otras medidas de desempeño pueden consultarse en De Gooijer y Hyndman (2006).

En este artículo se propone el uso de un mecanismo de control, como es la señal de rastreo (TS), como indicador del desempeño histórico del modelo, entendiéndose que una señal de rastreo se calcula por período mediante la expresión (8) (Makridakis, Wheelwright y Hyndman, 1998) y permite determinar si el modelo a través del tiempo ha obtenido buenas proyecciones y si éstas se encuentran dentro de los límites admisible de error (límites de control) definidos por la gerencia:

La TS se mide en desviaciones absolutas medias, por lo que se espera que cumpla con dos condiciones: (1) que los valores obtenidos en cada período se encuentren dentro de los límites de control definidos y (2) que sus valores en el tiempo sean tanto positivos como negativos, lo que indica que el modelo ha compensado en el tiempo los errores positivos con los negativos y viceversa (Makridakis, Wheelwright y Hyndman, 1998). De lo anterior se concluye que, cuanto menores sean las magnitudes de las señales de rastreo y los valores obtenidos de éstas a través del tiempo sean tanto positivos como negativos, el modelo se encuentra bajo control y su desempeño será más eficiente que aquellos modelos que no tienen este tipo de comportamiento. Finalmente, el indicador propuesto en este artículo para medir la exactitud del modelo es el rango de la señal de rastreo, que se calcula mediante la expresión:

El cálculo de las proyecciones aplicando el modelo de suavización de Holt y de las medidas de desempeño para una serie completa de datos, expresadas en las fórmulas 6, 7 y 9, se muestra en la tabla 1. Los valores de α y β, para propósitos ilustrativos, se definieron en 0,3 y 0,4 respectivamente y se utilizó la forma de inicio básica expresada en las fórmulas 4 y 5. Es importante resaltar que los valores para realizar los cálculos de las diferentes medidas de desempeño se realizaron a partir t=5, con el propósito de dar un tiempo de calentamiento al modelo que permita llevar a cabo mejor las actualización de los diferentes términos, y así se logra hacer comparaciones más objetivas.

En la sección 3 se muestran dos formas de obtener los parámetros α y β y los valores de inicio del modelo de Holt, mediante la medición del MAD y de MSE, que son los indicadores tradicionales para la medición de la exactitud de los modelos de series de tiempo, junto con el indicador TSR propuesto en este artículo.

Como se mencionó en la sección 1, algunos autores han investigado sobre la optimización de los parámetros α y β del modelo de Holt, definiendo el MAD o el MSE como la función objetivo por minimizar y utilizando formas sencillas para hallar los valores de inicio del modelo, como la mostrada en la sección 2. Otros, por su parte, han incluido los parámetros α y β y los valores de inicio en el modelo de optimización, con las mismas funciones objetivo por minimizar. En ambas situaciones se busca obtener el conjunto de estos valores para que el modelo obtenga los mejores resultados en términos de la magnitud media del error, pero sin considerar cómo ha sido el desempeño histórico del modelo para obtener este resultado, el cual se puede medir por medio de la señal de rastreo.

Para poder efectuar las comparaciones pertinentes entre la forma como normalmente se han venido definiendo los parámetros α y β y los valores de inicio del modelo de Holt, a un mismo conjunto de datos de demanda se le aplicó el siguiente método:

• Optimización de parámetros α y β:

– Se definieron como valores de inicio los expresados en las ecuaciones 4 y 5.

– Se encontró el conjunto de valores de los parámetros α y β que minimizaran MAD, MSE y TSR.

– Se calculó la señal de rastreo para cada una de las proyecciones obtenidas con cada par de parámetros α y β.

• Optimización de parámetros α y β y de valores de inicio:

– Se encontraron el conjunto de valores de los parámetros α y β y de valores de inicio S₂ y T₂ que minimizaran MAD, MSE y TSR.

– Se calculó la señal de rastreo para cada una de las proyecciones obtenidas con el conjunto de parámetros α y β y de valores de inicio S₂ y T₂.

Es importante resaltar que los modelos de optimización empleados para minimizar el MAD, MSE y TSE son no lineales, ya que estas funciones son no lineales. Adicionalmente, en el caso donde se incluyen los valores de inicio S₂ y T₂ como variables de decisión en el modelo, se genera una multiplicación entre éstos y las otras variables de decisión (en este caso los parámetros α y β), creando una no linealidad. Lo anterior, sumado a la utilización de la función Min() principalmente para la función TSR, hacen que el modelo encuentre múltiples mínimos locales, que deberán ser analizados por el usuario para seleccionar la mejor combinación de los valores de las variables de decisión.

A continuación se muestran los modelos utilizados en ambos casos y los resultados obtenidos.

3.1 Optimización de parámetros α y β

En la figura 1 se muestra la información que debe ser ingresada a Solver para encontrar los valores de los parámetros α y β del modelo de suavización de Holt. Además se muestran los resultados obtenidos al minimizar las tres funciones objetivo empleadas.

Se observa que al minimizar el MAD o el MSE, los valores de los parámetros α y β son muy similares y que la diferencia entre los valores mínimos alcanzados con base en sus mediciones es de menos del 1%. Por otra parte, si se comparan estos resultados con los obtenidos con la minimización del TSR, el valor del MAD es un 70 % mayor y el del MSE un 250 %, los cuales son valores muy altos si se efectúa únicamente un análisis desde este punto de vista.

En la figura 2 se observa que el comportamiento de la señal de rastreo al optimizar el MAD o el MSE con sus respectivos parámetros α y β presenta un sesgo positivo lo que indica que para este caso el modelo hace subestimaciones de las proyecciones consistentemente. Por su parte, para el caso en que se minimiza el TSR, se observa que todos los puntos de la señal de rastreo se encuentran dentro de los límites de control de ±3MAD, con valores tanto positivos como negativos, lo que representa el comportamiento esperado, ya que indica una compensación histórica en los errores obtenidos en las proyecciones, lo cual finalmente se traduce en un mejor desempeño del modelo.

3.2 Optimización de parámetros α y β y de valores de inicio

El modelo utilizado en Solver para los casos en que los parámetros α y β y los valores iniciales son considerados como las variables por encontrar para optimizar las medidas de desempeño explicadas se muestra en la figura 3.

En este caso se observa que al minimizar la MAD o el MSE la diferencia entre los valores mínimos alcanzados con base en sus mediciones está entre un 6 % y un 11 %, respectivamente; los valores de los parámetros α y β encontrados son similares y existe alguna diferencia, aunque no muy marcada, en los valores de inicio. Todo lo anterior indica la necesidad de incluir tanto los parámetros α y β como los valores de inicio en la optimización, ya que existe un efecto considerable en los resultados obtenidos. Ahora, si se comparan los valores óptimos de MAD y MSE con los valores obtenidos para estas mismas medidas de desempeño cuando se minimiza el TSR, el incremento es de un 32 % y un 48 % en su orden, reduciéndose en forma notable las diferencias en relación con lo expuesto en la sección 3.1, mejorando altamente los resultados. En la figura 4 se muestran de nuevo las señales de rastreo del modelo de Holt con los parámetros y valores de inicio hallados, donde puede observarse como los modelos, cuando se optimiza MAD o MSE, mejoran su desempeño, si bien es claro que el del MSE tiene un desempeño superior en comparación con el del MAD, ya que los valores de su señal de rastreo se encuentran dentro de los límites de control especificados.

Tanto el modelo de MIN MSE como el MIN TSR presentan un comportamiento adecuado dentro de los límites de control, pero el modelo de MIN TSR exhibe un comportamiento superior, puesto que tiene mayor simetría y control en la señal de rastreo, lo cual se prueba con un rango menor de la señal de rastreo de cerca de un 45 %.

Al comparar los resultados de los valores obtenidos de la optimización de las tres medidas de desempeño utilizadas para tal fin, en la tabla 2 se evidencia que, independiente de la función objetivo que se utilice, todos los resultados presentan una mejora significativa, que se traduce en una disminución de todas las medidas de desempeño, cuando se incluyen los valores de inicio como variables en el modelo de optimización en comparación del caso en que no se incluyen.

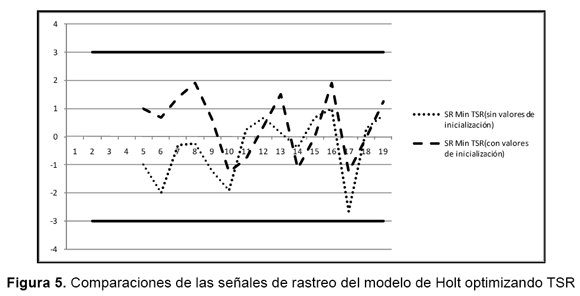
Se puede observar en las diferentes señales de rastreo obtenidas que el desempeño histórico del modelo es superior cuando se utiliza la minimización del rango de la señal de rastreo TSR, ya sea que se incluyan o no los valores de inicio en el modelo de optimización. Si se comparan los resultados obtenidos contra las otras dos funciones objetivo utilizadas, puede observarse que, aunque hay un aumento poco significativo en los valores del MAD y del MSE, se obtiene una disminución importante en el rango de la señal de rastreo. Así, por ejemplo, para el modelo de MIN MSE los valores mínimo y máximo de la señal de rastreo fueron (-2,134MAD; 2,454MAD) lo que da un rango de 4,5884 (ver figura 5) que equivale en unidades a (-114,30; 131,44), ya que cada MAD es de 53,5646 unidades, en comparación con el modelo de MIN TSR donde los valores mínimos y máximos de la señal de rastreo fueron de (-1,237MAD; 1,920MAD) dando un rango de 3,1567 (ver tabla 2), lo que corresponde en unidades a (-81,70; 127,53), comprobando de nuevo que el modelo en el cual se minimiza el rango de la señal de rastreo presenta un mejor desempeño y control.

Finalmente, la señal de rastreo cuando se minimiza el TSR y se incluyen los valores de inicio en la optimización presenta un comportamiento mucho más simétrico y se encuentra bajo más control que la señal de rastreo cuando se minimiza el TSR sin incluir estos valores, tal y como se muestra en la figura 5, lo cual demuestra la necesidad de incluir los valores de inicio en el modelo de optimización para mejorar el desempeño del modelo de suavización de Holt.

El modelo de suavización de Holt requiere la definición de los parámetros α y β y los valores de inicio para poder realizar las proyecciones. Algunos autores han trabajado sobre la necesidad de optimizar estas variables para obtener resultados que mejoren el desempeño del modelo por medio de la minimización de alguna función objetivo que mide su comportamiento de una manera agregada, pero que no considera el desempeño histórico, lo que se puede traducir en subestimaciones o sobreestimaciones consistentes en el tiempo.

En este artículo se propone una nueva forma de obtener los parámetros α y β y los valores de inicio del modelo de Holt, a partir de la minimización del rango de la señal de rastreo, que permite mejorar su desempeño mediante (1) la obtención de valores con indicadores clásicos en los pronósticos como son el MAD o el MSE, que garantizan una mayor exactitud del modelo de proyección empleado y (2) un rango bajo en la señal de rastreo logrando que el modelo esté históricamente bajo control.

Finalmente es ideal lograr un balance entre las medidas de desempeño como la desviación absoluta media, el error cuadrático medio y la señal de rastreo, con el fin de obtener modelos de proyección mucho más robustos.

Billah, B.; King, M. L.; Snyder, R. D. and. Koehle, A. B. (2006). "Exponential smoothing model selection for forecasting". International Journal of Forecasting, vol. 2, No. 22, pp. 239-247.        [ Links ]

Castro, C. A. Planeación de Producción. Medellín: Fondo Editorial Universidad Eafit, 2008.        [ Links ]

De Gooijer, J. G. and Hyndman, R. J. (2006). "25 years of time series forecasting". International Journal of Forecasting, vol. 3, No. 22, pp. 443-473.        [ Links ]

Gardner, E. S. (1985). "Exponential smoothing: the state of the art". Journal of Forecasting, vol. 4, No. 1 (March), pp. 1-28.        [ Links ]

Gardner, E. S. (2006). "Exponential smoothing: the state of the art - Part II". International Journal of Forecasting, vol. 4, No. 22, pp. 637-666.        [ Links ]

Gelper, S.; Fried, R. and Croux C. (2010). "Robust forecasting with exponential and Holt-Winters smoothing". Journal of Forecasting, vol. 3, No. 29, pp. 285-300.        [ Links ]

Heizer, J. y Render B. Principios de administración de operaciones. México: Pearson, 2009.        [ Links ]

Holt, C. C. Forecasting seasonals and trends by exponentially weighted moving averages. ONR Memorandum No. 52. Pittsburgh, PA: Carnegie Institute of Technology, 1957.        [ Links ]

Küsters, Ulrich; McCullough, B. D. and Bell, Michael (2006). "Forecasting software: past, present and future". International Journal of Forecasting, vol. 22, No. 3, pp. 599-615.        [ Links ]

Makridakis, S. G.; Wheelwright S. C. and Hyndman. R. I. Forecasting: methods and applications. New York: John Wiley & Sons, 1998.        [ Links ]

Rasmussen, R. (2004). "On time series data and optimal parameters". Omega, vol. 2, No. 32, pp. 111-120.        [ Links ]

Rey, M. F. Encuesta Nacional Logística - Colombia 2008. Resultados del benchmarking logístico empresarial. Documento de Discusión. Latin America Logistics Center (LALC). 2008.        [ Links ]

Sanders, N. R. and Manrodt, K. B. (2003). "Forecasting oftware in practice: use, satisfaction, and performance". Interfaces, vol. 33, No. 5 (Sep.-Oct.), pp. 90-93.        [ Links ]

Syntetos, Aris A.; Boylan, J. E. and Disney, Stephen M. (2009) "Forecasting for inventory planning: a 50-year review". Journal of the Operational Research Society, No. 60, pp. 149-160.        [ Links ]