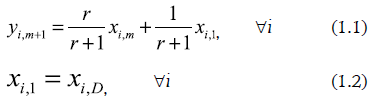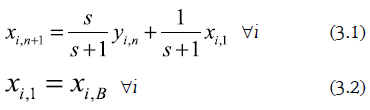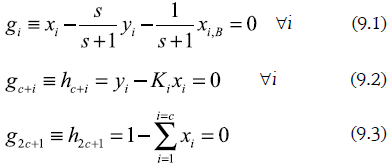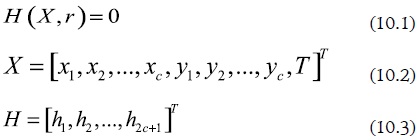Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.16 Envigado July/Dec. 2011
CÁLCULO E INTERPRETACIÓN DE LAS TRAYECTORIAS DE PUNTOS DE COMPOSICIÓN CONSTANTE (PINCH) EN COLUMNAS SIMPLES DE DESTILACIÓN PARA MEZCLAS AZEOTRÓPICAS HOMOGÉNEAS
CALCULATION AND INTERPRETATION OF THE PINCH POINTS TRAJECTORIES IN SIMPLE DISTILLATION COLUMNS FOR HOMOGENEOUS AZEOTROPIC MIXTURES
CÁLCULO E INTERPRETAÇÃO DAS TRAJETÓRIAS DE PONTOS DE COMPOSIÇÃO CONSTANTE (PINCH) EM COLUNAS SIMPLES DE DESTILAÇÃO PARA MISTURAS AZEOTRÓPICAS HOMOGÊNEAS
César Augusto Sánchez*
*Ingeniero Químico, Universidad Nacional de Colombia sede Manizales; Magíster (c) en Ingeniería Química e Investigación, Universidad Nacional de Colombia sede Bogotá. Docente Investigador, Departamento de Ingeniería Química, Universidad de América. Bogotá, Colombia. cesar.sanchez@profesores.uamerica.edu.co
Artículo recibido 21-II-2011. Aprobado 30-IX-2011
Discusión abierta hasta junio de 2012
RESUMEN
Se presenta un método de continuación del tipo predictor-corrector para trazar completamente los ramales de puntos de pinch asociados con los productos o seudoproductos de una columna de destilación azeotrópica homogénea. El método trata fácilmente con los puntos de retorno permitiendo la localización de los puntos pinch del tipo tangente. El concepto se fundamenta en las ideas de Fidkowski, Malone y Doherty, pero incluye algunas novedades, como la estrategia de iniciación de los cálculos, la forma de obtener el vector tangente y el grupo de ecuaciones sobre el cual se aplica la técnica. Se ilustran tres ejemplos con las soluciones de acetona + cloroformo + benceno, acetona + cloroformo + metanol y ácido acético + amilalcohol + amilacetato, enfatizando en casos que muestran mejores posibilidades de separación en la condición de reflujo finito que en la operación con reflujo total.
PALABRAS CLAVE: puntos pinch; métodos de continuación; destilación azeotrópica; mapas de destilación.
ABSTRACT
A continuation method of the kind predictor-corrector is presented for completely tracking of the pinch points branches related to the products or pseudoproducts of a homogeneous azeotropic distillation column. The method easily handles the turning points allowing the localization of the tangent pinch points. The foundation of the concept is in the ideas of Fidkowski, Malone y Doherty; however, some novelties are included, as the initiation strategy for calculations, the way to obtain the tangent vector and the set of equations on which the technique is applied. Three examples are illustrated with the solutions of acetone + chloroform + benzene, acetone + chloroform + methanol and acetic acid + amyl alcohol + amyl acetate, emphasizing cases that show better separation possibilities in the finite reflux condition than with total reflux operation.
KEY WORDS: pinch points; continuation methods; azeotropic distillation; distillation maps.
RESUMO
Apresenta-se um método de continuação do tipo preditor-corretor para traçar completamente os ramos de pontos de pinch associados com os produtos ou pseudoprodutos de uma coluna de destilação azeotrópica homogénea. O método trata facilmente com os pontos de retorno permitindo a localização dos pontos pinch do tipo tangente. O conceito fundamenta-se nas ideias de Fidkowski, Malone e Doherty, mas inclui algumas novidades, como a estratégia de iniciação dos cálculos, a forma de obter o vetor tangente e o grupo de equações sobre o qual se aplica a técnica. Ilustram-se três exemplos com as soluções de acetona + clorofórmio + benzeno, acetona + clorofórmio + metanol e ácido acético + amilálcool+ amilacetato, enfatizando em casos que mostram melhores possibilidades de separação na condição de refluxo finito que na operação com refluxo total.
PALAVRAS-CÓDIGO: pontos pinch; métodos de continuação; destilação azeotrópica; mapas de destilação.
1. INTRODUCCIÓN
Al considerar los resultados de la solución del modelo de equilibrio para columnas de destilación con infinito número de etapas, se encuentran secciones de composición constante denominadas regiones "pinch". La posición de estas regiones en el espacio de composiciones es función del reflujo y de los productos de destilación (destilados y fondos). El conocimiento de la composición de las regiones pinch resulta importante en la primera aproximación al diseño aplicando métodos de carácter geométrico, siendo necesario en la localización de la región de productos y el cálculo del reflujo mínimo.
El primer nivel del diseño de una columna de destilación consiste en desarrollar las siguientes tareas (Fidkowski, Malone y Doherty, 1991; Castillo, Thong y Towler, 1998; Petlyuk, Danilov y Serafimov, 2008): a) investigar las condiciones de separabilidad (determinar si es posible la separación propuesta como objetivo de diseño); b) investigar las condiciones de mínimo consumo de energía (cálculo del reflujo mínimo); c) localizar la etapa de alimentación y cálculo del número de etapas teóricas para un reflujo de operación finito y superior al mínimo. En un segundo nivel del diseño se obtienen los requisitos de hardware: diámetro de la columna, selección del tipo de empaque o del tipo de plato y predicción del desempeño para ajustarlo al diseño. A este respecto es importante observar que los simuladores comerciales son especialmente útiles en la evaluación del desempeño, pero no resultan herramientas prácticas en las tareas del diseño conceptual y la síntesis de procesos de destilación (Petlyuk y Danilov, 2001; Danilov, Petlyuk y Serafimov, 2007; Petlyuk, Danilov y Serafimov, 2008). Por ejemplo, la localización de la región de composición de productos (o región de corbatín), la determinación rigurosa del reflujo mínimo y la localización de la etapa de alimentación exigen dispendiosos estudios paramétricos en un simulador comercial. La razón de esto estriba en que los métodos iterativos que resuelven un modelo particular (sea este de equilibrio o de no equilibrio) encuentran las variables de salida (la composición del destilado y los fondos) para unas "dimensiones" específicas de la columna (por ejemplo, el número de etapas, la relación de reflujo, etc.), lo que resulta contrario al proceso de diseño, donde se conocen las variables de salida y se trata de encontrar las dimensiones necesarias para realizar estas especificaciones.
Los métodos existentes en la literatura consultada para tratar el primer nivel de diseño requieren las trayectorias de destilación reversible asociadas con los productos y la alimentación; o en un análisis un poco más simplificado (pero más frecuente), las trayectorias de puntos pinch (TPP) asociadas con una columna con la hipótesis de flujo molar constante (Julka y Doherty, 1990; Koehler, Aguirre y Blass, 1991;Wahnschafft et al., 1992; Julka y Doherty, 1993; Koehler, Poellmann y Blass, 1995; Lucia, Amale y Taylor, 2008; Petlyuk, Danilov y Serafimov, 2008). Algunos aspectos concretos que pueden investigarse por medio de la interpretación de las TPP son: a) la posibilidad de cruzar una separatriz termodinámica; b) la existencia no sólo de un reflujo mínimo sino también de un reflujo máximo; c) el espacio de composiciones donde se encuentran contenidos todos los perfiles de las secciones de rectificación y agotamiento.
Lucia, Amale y Taylor (2008) así como Felbab, Hildebrandt y Glasser (2010) realizaron una breve revisión de los métodos más relevantes disponibles en la literatura para el cálculo de los puntos pinch, concluyendo que los métodos existentes sufrían de uno o varios de los siguientes problemas: 1) no pueden tratar configuraciones con múltiples alimentos; 2) no localizan todos los puntos; 3) sólo localizan un tipo específico de punto; 4) tienen problemas de convergencia con modelos termodinámicos complejos. Sin embargo, estos autores no realizaron las siguientes observaciones: 1) las configuraciones con dos alimentos, muy comunes en la destilación azeo- trópica y extractiva, pueden ser tratadas con el concepto de seudoproducto (Wahnschafft y Westerberg, 1993; Petlyuk y Danilov, 1999); 2) durante el diseño no son necesarios todos los ramales de puntos pinch (RPP) (Julka y Doherty, 1990; Fidkowski, Malone y Doherty, 1991; Julka y Doherty, 1993; Castillo, Thong y Towler, 1998); 3) los métodos de continuación pueden localizar todos los tipos de puntos sobre un ramal específico (Fidkowski, Malone y Doherty, 1991). Aunque el método de Felbab, Hildebrandt y Glasser (2010) puede localizar incluso los ramales fuera del espacio de composiciones (soluciones de las ecuaciones sin sentido físico, correspondientes a fracciones molares negativas) es un método de "fuerza bruta" porque explora el dominio de una función (en busca de los mínimos) dividiéndolo en subdominios y explorando después en todos los subdominios. En contraste con esto, los métodos de continuación, como el de Fidkowski, Malone y Doherty (1991), que emplea como parámetro el inverso de la relación de reflujo, o el de Poellmann y Blass (1994), con la temperatura como parámetro, tienen algunas ventajas que merecen ser señaladas: 1) proporcionan sentido físico al proceso de solución, porque corresponden con la variación de las soluciones de las ecuaciones frente a la variación de uno de los grados de libertad; a este respecto debe subrayarse que es más interesante el método de Fidkowski, Malone y Doherty (1991), porque la relación de reflujo debe obtenerse como resultado de la tarea del diseño; 2) obtienen provecho de la convergencia local del método de Newton-Raphson situando la aproximación en el radio de convergencia de éste (Seydel, 2010); 3) existen algunos algoritmos robustos para trazar la curva paramétrica originada por una técnica de continuación (Seydel y Hlavacek, 1987; Allgower y Georg, 1990; Choi, Harney y Book, 1996; Seydel, 2010).
El motivo de este trabajo es presentar y aplicar una modificación del método de continuación de Fidkowski, Malone y Doherty (1991) para trazar los RPP asociados con los productos o seudoproductos de una columna de destilación para fraccionar soluciones homogéneas altamente no ideales (por ejemplo, exhiben una o varias separatrices termodinámicas originadas por la presencia de azeótropos). Dos aspectos definen las diferencias: 1) Fidkowski, Malone y Doherty (1991) no incluyen en forma explícita las ecuaciones del equilibrio líquido vapor (ELV) en la curva paramétrica resultante de su análisis y resuelven el problema del ELV con una rutina "externa"; la desventaja de esto es que, para obtener la composición del vapor, la temperatura y sus derivadas numéricas, es necesario resolver por completo el problema del ELV, y en el caso de las derivadas, por lo menos dos veces; en la propuesta que sigue (ver sección 2) se incluirán las ecuaciones del ELV en forma explícita, con el fin de resolver este inconveniente; 2) Fidkowski, Malone y Doherty (1991) emplean los azeótropos y componentes puros como punto inicial para el trazado de los ramales; en la propuesta que sigue se"invierte" esta idea al proponer como posible emplear las TPP para localizar los azeótropos presentes en un sistema (en especial los azeótropos del tipo silla) y emplear como punto inicial de los ramales la solución de los balances de materia en una sección de la columna para un número elevado de etapas (por ejemplo, 1000). La implementación se basa una estrategia del tipo "predictor-corrector" y la reparametrización típica con la longitud de arco para manejar los puntos de retorno (Lin, Seader y Wayburn, 1987; Allgower y Georg, 1990; Fidkowski, Malone y Doherty, 1991; Choi, Harney y Book, 1996; Seydel, 2010). El determinante de la jacobiana es observado mientras se calcula una trayectoria, con el fin de localizar los puntos de bifurcación nodo-silla. Este tipo de bifurcación resulta importante porque los puntos pinch tangentes corresponden siempre con ella (Fidkowski, Malone y Doherty, 1991; Torres y Espinosa, 2009).
Se ilustran ejemplos de aplicación de la metodología propuesta con las soluciones azeotrópicas constituidas por los sistemas ternarios ácido acético + amilalcohol + amilacetato, acetona + cloroformo + benceno y acetona + cloroformo + metanol, en condiciones particularmente interesantes para ilustrar problemas comunes en procesos de destilación azeotrópica y extractiva, tales como la posibilidad de cruzar una separatriz termodinámica operando a reflujo finito, la presencia de puntos pinch del tipo tangente y la localización de la región de composiciones determinada por los perfiles de una sección de la columna. En los casos expuestos en este trabajo y en otros (Sánchez, 2011) estudiados en el grupo de investigación de Procesos de Separación no Convencionales (GPS), el método propuesto no presenta problemas de convergencia o inestabilidad numérica y se muestra como una herramienta de análisis cualitativo durante la síntesis de secuencias de separación por destilación.
2. TRANSFORMACIÓN DE LAS ECUACIONES PINCH EN CURVAS PARAMÉTRICAS
En la década de los ochenta, el grupo de investigación liderado por el estadounidense Michael F. Doherty publicó una serie de artículos sobre la síntesis y el diseño de procesos de destilación azeotrópica (Levy, Van Dongen y Doherty, 1985; Van Dongen y Doherty, 1985; Levy y Doherty, 1986a) presentando un método de diseño al que llamaron "de valores en la frontera", porque para ser aplicado precisa el conocimiento de la composición de los productos de la columna de destilación (el destilado y los fondos). Estas ideas fueron refinadas en la década de los noventa por el mismo grupo de investigadores (Julka y Doherty, 1990; Fidkowski, Malone y Doherty, 1991; Julka y Doherty, 1993) dando lugar a una teoría completa para el diseño, fundamentada en métodos cortos. Llamando "método corto" al que no necesita la solución rigurosa y completa del conjunto de ecuaciones MESH (acrónimo en inglés para mass equilibrium sum enthalpy) para resolver los tres problemas fundamentales del primer nivel de diseño. El grupo de relaciones que suele emplearse se basa en las ideas de McCabe y Thiele (1925), donde la suposición más restrictiva es la hipótesis de flujo molar constante entre etapas (Treybal, 1981) y la aplicación da lugar a un conjunto de ecuaciones en diferencias llamadas mapas o trayectorias de destilación (Julka y Doherty, 1990; Julka y Doherty, 1993; Danilov, Petlyuk y Serafimov, 2007; Petlyuk, Danilov y Serafimov, 2008).
La figura 1 muestra la representación de la sección de enriquecimiento en una columna simple de destilación con un condensador total que entrega líquido saturado. Las etapas se cuentan en la dirección descendente y debe observarse que se considera flujo molar constante. Los balances globales de materia por componente conducen al mapa de destilación para la sección de rectificación:
Siendo r, la relación de reflujo externo, definida por el cociente:
La figura 2 representa la sección de agotamiento en una columna simple con un rehervidor parcial que entrega líquido saturado. Las etapas se cuentan en la dirección ascendente y se supone flujo molar constante. Los balances globales de materia por componente conducen al mapa de destilación para la sección de agotamiento:
Siendo s la relación de rehervido, definida por el cociente:
Un pinch ocurre cuando en una sección de la columna no se observa variación en la composición entre las etapas sucesivas de la sección, esto es:
En teoría esta condición puede obtenerse con infinitas etapas (Wahnschafft et al., 1992; Lucia, Amale y Taylor, 2008). Es decir que después de aplicar los mapas (1) y (3) para grandes valores de m (o de n) se obtiene un punto fijo o punto pinch. Al sustituir (5) en (1) y (3) obtenemos las ecuaciones que gobiernan los mapas de destilación en estas regiones de composición constante. Para las secciones de rectificación y agotamiento se tiene respectivamente:
El grupo de ecuaciones (6) o (7) debe ser completado con las ecuaciones del ELV, porque las condiciones de equilibrio de fases también se cumplen en las regiones de composición constante de la columna. Por otra parte, al tomar todas las fracciones molares como independientes, deberán considerarse ecuaciones adicionales indicando que la suma de estas debe ser la unidad. Y puede probarse (Koehler, Aguirre y Blass, 1991; Petlyuk y Danilov, 1998; Petlyuk, Danilov y Serafimov, 2008) que los mapas (6) y (7) corresponden de modo exacto con las trayectorias de destilación reversible asociadas con los productos de cabeza y de fondos, para una columna simple de destilación con secciones adiabáticas con la hipótesis de flujo molar constante.
En síntesis, el conjunto completo de ecuaciones que determinan un pinch sobre el mapa de destilación de la sección de enriquecimiento, escrito en forma de funciones de discrepancia es:
Y el conjunto completo para la sección de agotamiento es:
Las relaciones (8.2) y (9.2) corresponden con el ELV. Ki es el coeficiente de distribución del componente i, el cual depende de la temperatura, la presión y la composición, en acuerdo con el modelo termodinámico empleado para la descripción del comportamiento de las fases.
La propuesta de Fidkowski, Malone y Doherty (1991) consistió en tratar los mapas (8.1) y (9.1) como curvas paramétricas en las relaciones de reflujo y de rehervido, respectivamente. Las ecuaciones del equilibrio de fases ((8.2) ó (9.2)) no fueron incluidas en la deformación, y el método de continuación se aplicó sólo sobre los mapas de destilación. Esto tiene la ventaja de reducir el número de ecuaciones que es necesario manipular en forma simultánea y también tiene dos inconvenientes: 1) la composición de una de las fases y la temperatura deben obtenerse resolviendo por completo el problema del ELV; 2) las derivadas de la composición de una fase y de la temperatura requieren resolver varias veces el problema del ELV (al menos dos veces, en el caso de obtener las derivadas aplicando diferencias finitas). Para tratar estos dos inconvenientes, en este trabajo se propone incluir el grupo completo de ecuaciones en la definición de la curva paramétrica. Por ejemplo, para representar los RPP de la sección de rectificación, a partir de (8):
Y para representar los RPP de la sección de agotamiento, a partir de (9):
Y puede afirmarse que las curvas paramétricas X(r) y X(s) que satisfacen (10.1) y (11.1) corresponden con las TPP asociadas con los productos de la columna de destilación. El trazado de estas trayectorias puede efectuarse con técnicas de continuación (Allgower y Georg, 1990; Seydel, 2010). Algunos detalles en este sentido se ofrecen en la siguiente sección.
3. ESTRATEGIA DE SOLUCIÓN POR CONTINUACIÓN
Los ingredientes básicos para trazar una curva originada en un análisis de continuación, una deformación o una homotopía, con métodos del tipo predictor-corrector son: 1) estrategias para calcular el vector tangente inducido por la jacobiana; 2) elección de la parametrización que permita trazar de manera estable los puntos de retorno; 3) estrategias para resolver el sistema algebraico no lineal originado en la etapa de corrección, en especial la aproximación de los puntos singulares cuando el parámetro es la longitud de arco; 4) el cálculo del tamaño de paso adecuado para la etapa de predicción (Seydel y Hlavacek, 1987; Allgower y Georg, 1990; Choi, Harney y Book, 1996; Seydel, 2010).
En este trabajo se sigue la manera tradicional de tratar los puntos singulares, empleando la descomposición ortogonal de Householder (Allgower y Georg, 1990; Kincaid y Cheney, 1994; Seydel, 2010) para obtener el vector tangente inducido y resolver, en el sentido de los mínimos cuadrados, la etapa de corrección. Fuera de la vecindad de las singularidades se emplea la eliminación de bloques de Keller (Lin, Seader y Wayburn, 1987) para obtener una solución exacta del vector tangente inducido y el método de Newton-Raphson para llevar a cabo la corrección. El parámetro escogido para seguir establemente los puntos de retorno es la longitud de arco. Es bien conocido que esta reparametrización permite seguir estos puntos singulares (Lin, Seader y Wayburn, 1987; Allgower y Georg, 1990; Fidkowski, Malone y Doherty, 1991; Choi, Harney y Book, 1996; Seydel, 2010). El tamaño de paso del predictor es "controlado" con el método recomendado por Seydel (2010), aunque fue necesario establecer un límite inferior y otro superior (sobre el tamaño del paso), con el fin de trazar "suavemente" los puntos de retorno y evitar el salto entre ramales (ver sección 4).
La aplicación de la eliminación de bloques de Keller (Lin, Seader y Wayburn, 1987) con el propósito de obtener el vector tangente no tiene antecedentes en la literatura consultada y por esta razón será expuesta con brevedad. Tomaremos por caso el RPP para la sección de rectificación (ecuación (10.1)), esto es, la curva paramétrica X(r). Al cambiar el parámetro de una curva monoparamétrica por la longitud de arco se obtiene la ecuación de Davidenko (Allgower y Georg, 1990; Sánchez, Estupiñán y Salazar, 2010), que para la situación sería:
La matriz de coeficientes en (12) es llamada matriz aumentada y el vector de derivadas, vector tangente inducido por esta. Hx es la matriz cuadrada con las derivadas de las funciones H con respecto a X ("la jacobiana"), Hr es un vector columna con las derivadas de las funciones H con respecto al reflujo y 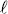 es la longitud de arco. Al aplicar la eliminación de bloques sobre el sistema formado por (12), se obtiene la siguiente ecuación cuadrática para el último elemento del vector tangente:
es la longitud de arco. Al aplicar la eliminación de bloques sobre el sistema formado por (12), se obtiene la siguiente ecuación cuadrática para el último elemento del vector tangente:
Siendo α y β la solución de los siguientes sistemas lineales:
Y los elementos restantes del vector tangente, la combinación lineal:
La ecuación 13 tiene dos soluciones reales simétricas, siendo una el negativo de la otra. Las relaciones (13), (14) y (15) proporcionan una solución exacta para el vector tangente y entonces no es necesario aproximarlo, como en la mayor parte de los trabajos, donde es intercambiado por una secante (Allgower y Georg, 1990; Wasylkiewicz, Doherty y Malone, 1999; Wasylkiewicz, Kobylka y Castillo, 2003; Seydel, 2010).
4. EJEMPLOS Y DISCUSIÓN
Para ilustrar la aplicación de las ideas se eligieron tres mezclas ternarias altamente no ideales (exhiben una o varias separatrices termodinámicas originadas por la presencia de azeótropos) representativas de situaciones que pueden tratarse o encontrarse en la práctica durante el estudio de las regiones de composición de productos, las condiciones de separabilidad o el análisis de los requisitos mínimos de energía. El objetivo es trazar los RPP "accesibles", a partir de los productos de cabeza y fondos, y obtener algunas consecuencias cualitativas sobre la síntesis y el diseño.
El primer ejemplo tiene que ver con las soluciones de acetona + cloroformo + benceno. Es el caso más citado en la literatura revisada y uno de los primeros sistemas en los que se probó la posibilidad de cruzar una separatriz termodinámica que opera en condiciones de reflujo finito (Levy, Van Dongen y Doherty, 1985; Wahnschafft et al., 1992; Castillo, Thong y Towler, 1998). Se ilustra esta situación y la existencia de varios RPP. El segundo ejemplo trata con las soluciones de acetona + cloroformo + metanol y es interesante porque presenta cuatro azeótropos con índices topológicos diferentes (nodos binario estable, binario inestable, binario silla y ternario silla), lo que da lugar a uno de los mapas de curvas de destilación (o de residuo) más complejos, entre los posibles para los sistemas ternarios. En este caso se muestra la posibilidad de cambiar de región de destilación dos veces en una misma columna. Por fin, el tercer ejemplo involucra las soluciones de ácido acético + amilalcohol + amilacetato. Su importancia consiste en mostrar que la existencia de una bifurcación en los perfiles de una sección de una columna no necesariamente conlleva cruzar una separatriz.
En todos los casos la fase gaseosa fue tratada con la teoría química (Hayden y O'Connell, 1975; Prausnitz, Lichtenthaler y Azevedo, 2000) y con los parámetros de asociación y solvatación reportados por Prausnitz et al. (1980). Este tratamiento es en especial necesario para las soluciones de ácido acético + amilalcohol + amilacetato, donde debe tenerse en cuenta la asociación y solvatación del ácido en la fase gaseosa. Para la no idealidad de la fase líquida se usó el modelo NRTL (Renon y Prausnitz, 1968) con los parámetros binarios de interacción como sigue: a) para las soluciones de acetona + cloroformo + benceno y acetona + cloroformo + metanol se tomaron de Kurihara, Hori y Kojima (1998); b) para las soluciones de ácido acético + amilalcohol + amilacetato se tomaron de Chiang et al. (2002). Las ecuaciones para la presión de vapor y la densidad de los líquidos puros son la de Yaws (2003) y la de Yaws (2008), respectivamente. El coeficiente de distribución se calculó entonces con la siguiente relación (Smith, Van Ness y Abbott, 2005):
La primera tarea consistió en la localización de todos los azeótropos y las separatrices termodinámicas. Esta caracterización es esencial porque determina el número de regiones de destilación y las limitantes a la separación existentes a reflujo infinito. Para comparación, la tabla 1 presenta los azeótropos calculados con el modelo empleado en la descripción del ELV, los datos reportados en la literatura y el error absoluto asociado. Existe una buena correspondencia, según se deduce de la observación de las desviaciones tabuladas. El modelo termodinámico es aceptable, porque describe en forma adecuada la topología del mapa de líneas de destilación en la condición de reflujo infinito.
Para obtener el primer punto pinch sobre un ramal se aplica el mapa de destilación de la sección correspondiente (ecuación 1.1 o 3.1) para un número de etapas igual a 1000. Debido a que los perfiles pueden bifurcarse, cuando los productos se encuentran cerca de la separatriz, del lado convexo, es necesario explorar esta posibilidad y en tal caso obtener dos puntos iniciales, uno sobre cada ramal. Tal exploración se efectúa con facilidad construyendo dos trayectorias de destilación: una a reflujo infinito (o línea de destilación) y otra con un reflujo cercano a cero (por ejemplo 0,1). Si los puntos finales de las dos trayectorias de destilación tienen una estabilidad diferente, entonces existe una bifurcación y por lo menos dos ramales son accesibles para el producto en consideración. Cuando los puntos finales de las trayectorias se encuentran en regiones de destilación diferentes no es necesario efectuar el análisis de estabilidad, porque en este caso necesariamente existe una bifurcación. Después de obtener una primera solución sobre un ramal, se aplica la técnica de continuación descrita en la sección 3, en las dos direcciones de la curva (positiva y negativa) hasta alcanzar un azeótropo, un componente puro o un producto de la columna de destilación.
El tamaño de paso empleado en la etapa de predicción se ajusta en cada punto de la curva atendiendo a dos consideraciones: a) si el punto es singular o cercanamente singular, se mantiene fijo en su valor mínimo (Δ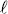 min=0,001); b) si el punto no es singular, se cuenta el número de iteraciones que requiere el método de Newton-Raphson para resolver el corrector y se incrementa si este número es menor que el óptimo, o se disminuye si resulta ser mayor (Seydel, 2010). Se observó la necesidad de imponer un límite superior al tamaño de paso (Δ
min=0,001); b) si el punto no es singular, se cuenta el número de iteraciones que requiere el método de Newton-Raphson para resolver el corrector y se incrementa si este número es menor que el óptimo, o se disminuye si resulta ser mayor (Seydel, 2010). Se observó la necesidad de imponer un límite superior al tamaño de paso (Δ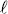 max=0,1) para evitar saltos entre ramales (en ocasiones, estos pasan muy cerca el uno del otro, ver por ejemplo la figura 5) y resultados del predictor fuera de la región de atracción del Newton-Raphson, en la proximidad de los puntos de retorno. El límite superior es bastante estricto y se eligió pensando más en la estabilidad numérica y en el seguimiento de los detalles de las curvas que en el tiempo de cómputo. Sin embargo, debido a que este proceso es excesivamente lento cerca de los puntos fijos a reflujo infinito (azeótropos y componentes puros), porque se necesitan grandes cambios relativos en la razón de reflujo para ocasionar cambios significativos en la composición y en la temperatura (Fidkowski, Malone y Doherty, 1991; Wahnschafft et al., 1992; Castillo, Thong y Towler, 1998), se eligió, sólo para este tipo de puntos fijos: Δ
max=0,1) para evitar saltos entre ramales (en ocasiones, estos pasan muy cerca el uno del otro, ver por ejemplo la figura 5) y resultados del predictor fuera de la región de atracción del Newton-Raphson, en la proximidad de los puntos de retorno. El límite superior es bastante estricto y se eligió pensando más en la estabilidad numérica y en el seguimiento de los detalles de las curvas que en el tiempo de cómputo. Sin embargo, debido a que este proceso es excesivamente lento cerca de los puntos fijos a reflujo infinito (azeótropos y componentes puros), porque se necesitan grandes cambios relativos en la razón de reflujo para ocasionar cambios significativos en la composición y en la temperatura (Fidkowski, Malone y Doherty, 1991; Wahnschafft et al., 1992; Castillo, Thong y Towler, 1998), se eligió, sólo para este tipo de puntos fijos: Δ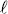 min =1 y Δ
min =1 y Δ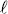 max =10.
max =10.
Los RPP se trazaron con una precisión numérica de 10-9, quiere esto decir que la norma euclidiana de los vectores H y G, en las ecuaciones 10.1 y 11.1, respectivamente, es menor o igual a este valor. En un computador con un procesador AMD Athlon 64x2 Dual Core 4800+ y 2,0 GB RAM, empleando en la implementación un lenguaje interpretado, el tiempo de cómputo para alguna de las trayectorias estudiadas es inferior a los tres minutos. Este resultado es aceptable, porque en un lenguaje compilado estaríamos hablando de unos cuantos segundos.
4.1 Acetona + cloroformo + benceno
La figura 3 muestra la estructura del espacio de concentraciones; existen una separatriz termodinámica y dos regiones de destilación. No es posible separar una solución de acetona + cloroformo + benceno en los componentes puros, operando a reflujo infinito. No obstante, es posible cruzar la separatriz en una operación a reflujo finito tal y como lo ilustra el primer RPP asociado con el producto B. Los perfiles en la sección de agotamiento (trayectorias azules) se bifurcan en s ≈ 4,25. Para s<4,25 los perfiles terminan sobre el primer RPP y para s>4,25 terminan sobre el segundo ramal. Obsérvese que apenas una porción de las trayectorias es accesible por los perfiles de la sección de agotamiento, lo que significa que no es posible trazar los ramales de puntos pinch completos únicamente por la aplicación de los mapas de destilación. Alguna técnica adicional (por ejemplo, el método de continuación descrito en este trabajo) deberá desarrollarse para trazar una curva completa. El segundo RPP presenta un punto de retorno en s = 2,60 (denotado como M en la figura 3), por esta razón, para s>2,60 el problema tiene tres soluciones, y para s<2,60 tiene una solución. Wahnschafft et al. (1992) y Petlyuk (1998) mostraron que es posible tener el producto B sobre el lado cloroformo benceno y, en consecuencia, separar una mezcla que se encuentre en la región de destilación cuyos nodos son acetona-azeótropo binario-benceno, en los componentes puros, por el uso de dos columnas sin recirculación entre ellas.
4.2 Acetona + cloroformo + metanol
La figura 4 muestra la estructura del espacio de concentraciones: existen cuatro separatrices termodinámicas y cuatro regiones de destilación. No es posible separar una solución de acetona + cloroformo + metanol en los componentes puros, operando a reflujo infinito. Tampoco es posible lograr esto a reflujo finito. No obstante, debe observarse que las posibilidades de separación a reflujo finito son más amplias que a reflujo infinito. Como prueba de ello, en la figura 4 se ilustra un caso en el que el primer RPP, asociado con el destilado D, cruza dos veces la separatriz; por lo tanto, este destilado puede ser obtenido con alimentos en tres regiones diferentes. Los perfiles en la sección de rectificación (trayectorías azules) se bifurcan en r ≈ 6,95. Para r<6,95 los perfiles terminan sobre el primer RPP y para r>6,95 terminan sobre el segundo. Este último ramal presenta un punto de retorno (indicado con M en la figura 4) en r = 1,22, implicando que el problema tiene tres soluciones para r>l,22 y una solución para r<l ,22. Debido a que se trata de un condensador total, el primer RPP no empieza con la composición del destilado sino con la composición del líquido en la etapa 2 (denotado por X2 en la figura 4), indicando que el proceso sólo podría llegar a considerarse reversible a partir de la etapa 2. Finalmente, la observación del segundo ramal en las figuras 3 y 4, permite afirmar lo siguiente: cuando una trayectoria conecta dos puntos fijos (azeótropos y componentes puros), deberá existir al menos un punto de retorno porque los puntos fijos sólo son accesibles en la condición de reflujo infinito.
4.3 Ácido acético + amilalcohol + amilacetato
La figura 5 muestra la estructura del espacio de concentraciones: existen cuatro separatrices termodinámicas y cuatro regiones de destilación. No es posible separar una solución de ácido + alcohol + acetato en los componentes puros, operando a reflujo infinito. La idea importante en la figura 5 es la siguiente: el primer ramal cruza la separatriz y los perfiles de la sección de rectificación (trayectorias azules) no la cruzan. Es decir que, aunque los perfiles de una sección se bifurquen, no puede concluirse el cambio de región de destilación. Además de bifurcarse, los perfiles deben extenderse más allá de la separatriz termodinámica. Para cambiar de región de destilación los perfiles deben cruzar la separatriz antes de bifurcarse (comparar figuras 3 y 5).
Se concluye ilustrando un diagrama de bifurcación (fracción molar de ácido como una función de la relación de reflujo en el rehervidor) para un producto de fondos que presenta un punto pinch del tipo tangente (ver figura 6) sobre el único ramal alcanzable por la aplicación del mapa de destilación. Las fracciones molares de los otros componentes y la temperatura muestran un comportamiento similar. Se requiere un proceso de cálculo robusto para trazar con detalle una trayectoria como la ilustrada en la figura 6, porque el determinante de la jacobiana cambia de signo dos veces en una franja estrecha del reflujo (comprendida entre las rectas que pasan por M1 y M2). La importancia de localizar un punto del tipo tangente radica en que pueden llegar a controlar el valor del reflujo mínimo (Levy y Doherty, 1986b; Fidkowski, Malone y Doherty, 1991; Torres y Espinosa, 2009). Se citan aquí con el propósito de señalar que el algoritmo propuesto en este trabajo puede manejarlos sin inconvenientes.
5. CONCLUSIONES
Se presentó un método de continuación del tipo predictor-corrector que permite trazar completamente los ramales de puntos de pinch alcanzables por la aplicación de los mapas de destilación. El método maneja sin problemas los puntos de retorno permitiendo la localización de los puntos del tipo tangente.
Los ramales asociados con un producto de la columna de destilación no pueden localizarse por completo mediante la aplicación de los mapas de destilación, porque los puntos pinch generados por la aplicación de los mapas constituyen solamente un segmento del ramal. Este aspecto resalta el valor de la propuesta formulada debido a que constituye una alternativa de cálculo que supera la aplicación de los mapas de destilación con el fin de localizar los puntos fijos a reflujo finito.
Un ramal que conecte dos puntos fijos (azeótropos y componentes puros) deberá tener al menos un punto de retorno, porque los puntos fijos sólo son accesibles en la condición de reflujo infinito. Esta condición, al parecer obvia en el contexto de la teoría de los métodos de continuación, es la condición de los ramales que no contienen los productos de destilación y representan trayectorias de destilación reversible que no permiten obtener un producto específico.
Los ejemplos tratados sugieren una estrategia sencilla para la localización de los azeótropos ternarios del tipo silla, mediante la exploración de los productos de una columna de destilación y la construcción de los ramales de puntos pinch asociados, buscando un ramal que tenga su punto final en el azeótropo.
NOMENCLATURA
B: Flujo de los fondos, o se refiere al producto de fondos
c: Número de componentes
D: Flujo del destilado, o se refiere al destilado
g: Función de discrepancia en la sección de agotamiento
h: Función de discrepancia en la sección de rectificación
K: Coeficiente de distribución
L: Flujo del efluente líquido que abandona una etapa
p: Presión
r: Relación de reflujo
Rg: Constante de los gases
s: Relación de rehervido
T: Temperatura
v: Volumen específico de los líquidos puros
V: Flujo del efluente vapor que abandona una etapa
x: Fracción molar en la fase líquida
X: Vector columna que agrupa la composición de las fases y la temperatura
y: Fracción molar en la fase gaseosa
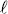 : Longitud de arco
: Longitud de arco
γ: Coeficiente de actividad
φ: Coeficiente de fugacidad de los componentes puros
 : Coeficiente de fugacidad de los componentes en solución
: Coeficiente de fugacidad de los componentes en solución
Subíndices
B: Se refiere a la sección de agotamiento
i: Se refiere al componente
m: Se refiere a la etapa
T: Se refiere a la sección de enriquecimiento
Superíndices
l: Correspondiente con el líquido
sat: En la condición de saturación
REFERENCIAS
Allgower, E. L. and Georg, K. Introduction to numerical continuation methods. USA: Colorado State University/Springer, 1990. 388 p. [ Links ]
Castillo, F. J.; Thong, D. Y. and Towler, G. P. (1998). "Homogeneous azeotropic distillation. 1. Design procedure for single-feed columns at nontotal reflux". Industrial & Engineering Chemistry Research, vol. 37, No. 3, pp. 987-997. [ Links ]
Chiang, S. F.; Lin, K. C.; Ching, Y. and Wong, D. (2002). "Design alternatives for the amyl acetate process: Coupled reactor/column and reactive distillation". Industrial & Engineering Chemistry Research, vol. 41, No. 13, pp. 3233-3246. [ Links ]
Choi, S. H.; Harney, D. A. and Book, N. L. (1996). "A robust path tracking algorithm for homotopy continuation". Computers & Chemical Engineering, vol. 20, No. 6-7 (June-July), pp. 647-655. [ Links ]
Danilov, R. Yu.; Petlyuk, F. B. and Serafimov, L. A. (2007). "Minimum-reflux regime of simple distillation columns". Theoretical Foundations of Chemical Engineering, vol. 41, No. 4, pp. 371-383. [ Links ]
Felbab, N.; Hildebrandt, D. and Glasser, D. (2010). "A new method of locating all pinch points in non ideal distillation systems, and its application to pinch point loci and distillation boundaries". Computers & Chemical Engineering, vol. 35, No. 6 (June), pp. 1072-1087. [ Links ]
Fidkowski, Z. T.; Malone, M. F. and Doherty, M. F. (1991). "Non ideal multicomponent distillation: Use of bifurcation theory for design". AIChE Journal, vol. 37, No. 12, pp. 1761-1779. [ Links ]
Hayden, J. G. and O'Connell, J. P. (1975). "A generalized method for predicting second virial coefficients". Industrial and Engineering Chemistry Process Design and Development, vol. 14, No. 3, pp. 209-216. [ Links ]
Horsley, L. H. Azeotropic data. USA: American Chemical Society, 1952. [ Links ]
Julka, V and Doherty, M. F. (1990). "Geometric behavior and minimum flows for nonideal multicomponent distillation". Chemical Engineering Science, vol. 45, No. 7, pp. 1801-1822. [ Links ]
Julka, V and Doherty, M. F. (1993). "Geometric nonlinear analysis of multicomponent non ideal distillation: A simple computer-aided design procedure". Chemical Engineering Science, vol. 48, No. 8, pp. 1367-1391. [ Links ]
Kincaid, D. y Cheney, W. Análisis numérico: Las matemáticas del cálculo científico. USA: Addison-Wesley Iberoamericana, 1994, pp. 231-284. [ Links ]
Koehler, J.; Aguirre, P. and Blass, E. (1991)."Minimum reflux calculations for nonideal mixtures using the reversible distillation model". Chemical Engineering Science, vol. 46, No. 12, pp. 3007-3021. [ Links ]
Koehler, J.; Poellmann, P. and Blass, E. (1995)."A review on minimum energy calculations for ideal and nonideal distillations". Industrial & Engineering Chemistry Research, vol. 34, No. 4, pp. 1003-1020. [ Links ]
Kurihara, K.; Hori, H. and Kojima, K. (1998)."Vapor-liquid equilibrium data for acetone + methanol + benzene, chloroform + methanol + benzene, and constituent binary systems at 101.3 kPa". Journal of Chemical Engineering Data, vol. 43, No. 2, pp. 264-268. [ Links ]
Levy, S. G. and Doherty, M. F. (1986a). "Design and synthesis of homogeneous azeotropic distillations. 4. Minimum reflux calculations for multiple-feed columns". Industrial & Engineering Chemical Fundamentals, vol. 25, No. 2, pp. 269-279. [ Links ]
Levy, S. G. and Doherty, M. F. (1986b). "A simple exact method for calculating tangent pinch points in multicomponent nonideal mixtures by bifurcation theory". Chemical Engineering Science, vol. 41, No. 12, pp. 3155-3160. [ Links ]
Levy, S. G.; Van Dongen, D. B. and Doherty, M. F. (1985). "Design and synthesis of homogeneous azeotropic distillations. 2. Minimum reflux calculations for nonideal azeotropic columns". Industrial & Engineering Chemical Fundamentals, vol. 24, No. 4, pp. 463-474. [ Links ]
Lin, W. J.; Seader, J. D. and Wayburn, T. L. (1987)."Computing multiple solutions to systems of interlinked separation columns". AIChE Journal, vol. 33, No. 6, pp. 886-897. [ Links ]
Lucia, A.; Amale, A. and Taylor, R. (2008). "Distillation-pinch points and more". Computers & Chemical Engineering, vol. 32, pp. 1342-1364. [ Links ]
McCabe, W. L. and Thiele, E. W. (1925). "Graphical design of fractionating columns". Industrial and Engineering Chemistry, vol. 17, No. 6, pp. 605-611. [ Links ]
Petlyuk, F. B. (1998). "Simple methods for predicting feasible sharp separations of azeotropic mixtures". Theoretical Foundations of Chemical Engineering, vol. 32, No. 3, pp. 245-253. [ Links ]
Petlyuk, F. B. and Danilov, R. Yu. (1998). "Calculations of distillation trajectories at minimum reflux for ternary azeotropic mixtures". Theoretical Foundations of Chemical Engineering, vol. 32, No. 6, pp. 548-559. [ Links ]
Petlyuk, F. B. and Danilov, R. Yu. (1999). "Sharp distillation of azeotropic mixtures in a two-feed column". Theoretical Foundations of Chemical Engineering, vol. 33, No. 3, pp. 233-242. [ Links ]
Petlyuk, F. B. and Danilov, R. Yu. (2001). "Theory of distillation trajectory bundles and its applications to the optimal design of separation units: Distillation trajectory bundles at finite reflux". Trans IChemE, vol. 79, Part A, pp. 733-746. [ Links ]
Petlyuk, F. B.; Danilov, R. Yu. and Serafimov, L. A. (2008). "Trees of reversible distillation trajectories and structure of trajectory bundles for sections of adiabatic columns". Theoretical Foundations of Chemical Engineering, vol. 42, No. 6, pp. 795-804. [ Links ]
Poellmann, P. and Blass, E. (1994). "Best products of homogeneous azeotropic distillations". Gas Separation & Purification, vol. 8, No. 4, pp. 194-228. [ Links ]
Prausnitz, J. M.; Anderson, T. F.; Grens, E. A.; Eckert, C. A.; Hsieh, R. and O'Connell, J. P. Computer calculations for multicomponent vapor-liquid and liquid-liquid equilibria. USA: Prentice Hall, 1980. pp. 160-178. [ Links ]
Prausnitz, J. M.; Lichtenthaler, R. N. y Azevedo, E. G. Termodinámica molecular de los equilibrios de fases. España: Prentice Hall Iberia, 2000. pp. 139-152. [ Links ]
Renon, H. and Prausnitz J. M. (1968). "Local compositions in thermodynamic excess functions for liquid mixtures". AIChE Journal, vol. 14, No. 1, pp. 135-144. [ Links ]
Sánchez, C. A. "Introducción al análisis y el diseño de columnas de destilación azeotrópica empleando métodos de continuación". Conferencia. XXI Encuentro Nacional de Estudiantes de Ingeniería Química y de Procesos. Bogotá, Colombia. (20-24 junio 2011). [ Links ]
Sánchez, C. A.; Estupiñán, L. y Salazar, M. A. (2010). "Herramientas para la caracterización termodinámica de sistemas ternarios en destilación". Revista EIA, año 7, No. 13 (julio), pp. 77-91. [ Links ]
Seydel, R. Practical bifurcation and stability analysis. 3rd ed. Berlin: Springer, 2010, pp. 169-261. [ Links ]
Seydel, R. and Hlavacek, V (1987). "Role of continuation in engineering analysis". Chemical Engineering Science, vol. 42, No. 6, pp. 1281-1295. [ Links ]
Smith, J. M.; Van Ness, H. C. and Abbott, M. M. Introduction to chemical engineering thermodynamics. 7th ed. New York: McGraw-Hill, 2005, pp. 545-551. [ Links ]
Tang, Y.; Chen, Y.; Huang, H. and Yu, C. (2005). "Design of reactive distillations for acetic acid esterification". AIChE Journal, vol. 51, No. 6, pp. 1683-1699. [ Links ]
Torres, K. A. and Espinosa, J. (2009). "Incorporating tangent pinch points into the conceptual modeling of batch distillations: Ternary mixtures". Industrial & Engineering Chemistry Research, vol. 48, No. 2, pp. 857-869. [ Links ]
Treybal, R. E. Mass-transfer operations. 3rd ed. Singapore: McGraw-Hill, 1981. pp. 402-423. [ Links ]
Van Dongen, D. B. and Doherty, M. F. (1985). "Design and synthesis of homogeneous azeotropic distillations. 1. Problem formulation for a single column". Industrial & Engineering Chemical Fundamentals, vol. 24, No. 4, pp. 454-463. [ Links ]
Wahnschafft, O. M.; Koehler, J. W.; Blass, E. and Westerberg, A. W. (1992). "The product composition regions of single-feed azeotropic distillation columns". Industrial & Engineering Chemistry Research, vol. 31, No. 10, pp. 2345-2362. [ Links ]
Wahnschafft, O. M. and Westerberg, A. W. (1993). "The product composition regions of azeotropic distillation columns. 2. Separability in two-feed columns and entrainer selection". Industrial & Engineering Chemistry Research, vol. 32, No. 6, pp. 1108-1120. [ Links ]
Wasylkiewicz, S. K.; Doherty, M. F. and Malone, M. F. (1999), "Computing all homogeneous and heterogeneous azeotropes in multicomponent mixtures". Industrial & Engineering Chemistry Research, vol. 38, No. 12, pp. 4901-4912. [ Links ]
Wasylkiewicz, S. K.; Kobylka, L. C. and Castillo, J. L. (2003), "Pressure sensitivity analysis of azeotropes". Industrial & Engineering Chemistry Research, vol. 42, No. 1, pp. 207-213. [ Links ]
Yaws, C. L. Yaws' handbook of thermodynamic and physical properties of chemical compounds: Physical, thermodynamic and transport properties for 5,000 organic chemical compounds. Norwich, NY: Knovel, 2003. [ Links ]
Yaws, C. L. Thermophysical properties of chemicals and hydrocarbons. USA: William Andrew, 2008. [ Links ]