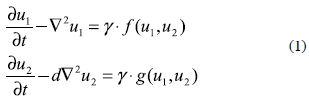Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.17 Envigado Jan./June 2012
PATRONES DE TURING SOBRE ESFERAS CON CRECIMIENTO CONTINUO
TURING PATTERNS ON SPHERES WITH CONTINUOUS GROWTH
PADRÕES DE TURING SOBRE ESFERAS COM CRESCIMENTO CONTÍNUO
Diego A. Garzón*, Angélica M. Ramírez**, Carlos A. Duque***
*Ingeniero Mecánico, Universidad Nacional de Colombia; Magíster en Ingeniería Mecánica, Universidad de los Andes; Doctor en Mecánica Computacional, Universidad de Zaragoza. Profesor Asociado e investigador, Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM), Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Bogotá, Colombia. dagarzona@bt.unal.edu.co.
**Ingeniera Mecánica, Universidad Nacional de Colombia; Doctora en Ingeniería Biomédica, Universidad de Zaragoza. Investigadora, Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM), Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Profesora Asociada, Departamento de Ingeniería Mecánica, Universidad Central de Colombia. Bogotá, Colombia. aramirez3@ucentral.edu.co.
***Ingeniero Mecánico, Universidad Nacional de Colombia; Magíster en Ingeniería Mecánica, Universidad de los Andes; Ph.D. en Ingeniería Mecánica, Universidad de Warwick. Profesor Asociado e investigador, Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM), Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Bogotá, Colombia. caduqued@bt.unal.edu.co.
Artículo recibido 28-III-2011. Aprobado 19-III-2012
Discusión abierta hasta diciembre de 2012
RESUMEN
En este artículo se desarrollan varios ejemplos numéricos sobre ecuaciones de reacción-difusión con dominio creciente, empleando el modelo de reacción de Schnakenberg, con parámetros en el espacio de Turing. Por tanto, se realizan ensayos numéricos sobre la aparición de los patrones de Turing en superficies esféricas. Para la solución de las ecuaciones de reacción-difusión se presenta un método de solución en superficies en tres dimensiones mediante el método de los elementos finitos con el uso de la formulación lagrangiana total. Los resultados muestran que la formación de los patrones de Turing depende de la velocidad de crecimiento de la superficie, el tipo de número de onda predicho en la teoría de dominios cuadrados y su tiempo de estabilización. Estos resultados pueden esclarecer algunos fenómenos de cambio de patrón en la superficie de la piel de los animales que exhiben manchas características.
PALABRAS CLAVE: reacción-difusión; Turing; lagrangiano total; elementos finitos; deformación de superficies.
ABSTRACT
We have developed several numerical examples of reaction-diffusion equations with growth surface domain. In this research we use the Schnakenberg reaction model, with parameters in the Turing space. Therefore, numerical tests are performed on the appearence of Turing patterns in spherical surfaces. For the solution of reaction diffusion equations provides a method of settling on surfaces in three dimensions using the finite element method under the total Lagrangian formulation. The results show that the formation of Turing patterns depends on the growth rate of the surface, the type of wave number predicted in the theory of square domains and their stabilization time. These results may explain some phenomena of pattern change on the surface of the skin of animals that exhibit characteristic spots.
KEY WORDS: reaction-diffusion; Turing; total Lagrangian; finite elements; deformation of surfaces.
RESUMO
Neste artigo desenvolvem-se vários exemplos numéricos sobre equações de reação-difusão com domínio crescente, empregando o modelo de reação de Schnakenberg, com parâmetros no espaço de Turing. Por tanto, realizam-se ensaios numéricos sobre o aparecimento dos padrões de Turing em superfícies esféricas. Para a solução das equações de reação-difusão apresenta-se um método de solução em superfícies em três dimensões mediante o método dos elementos finitos baixo o uso da formulação lagrangiana total. Os resultados mostram que a formação dos padrões de Turing depende da velocidade de crescimento da superfície, o tipo de número de onda predito na teoria de domínios quadrados e seu tempo de estabilização. Estes resultados podem esclarecer alguns fenômenos de mudança de padrão na superfície da pele dos animais que exibem manchas características.
PALAVRAS-CÓDIGO: reação-difusão; Turing; lagrangiano total; elementos finitos; deformação de superfícies.
1. INTRODUCCIÓN
Las ecuaciones de reacción-advección-difusión (RAD) (Babuška et al., 1995; Madzvamuse et al., 2002; Garzón-Alvarado, Martínez y Linero, 2011) y otros modelos más complejos, donde intervienen más especies o reactantes, poseen la capacidad para crear patrones espacio-temporales. Un caso particular de estos patrones son las inestabilidades de Turing (Madzvamuse et al., 2003; Garzón, 2007), que se caracterizan por la aparición de distribuciones de especies (patrones) estables en el tiempo e inestables en el espacio y con variadas aplicaciones (Hirayama y Takaki, 1988; Ardes, Busse y Wicht, 1997; Madzvamuse et al., 2002).
El análisis de estos sistemas de reaccióndifusión (RD) que presentan inestabilidad de Turing se ha desarrollado tradicionalmente mediante dos marcos de trabajo: análisis matemático (Mei, 2000) y simulación numérica (Madzvamuse, 2000; Madzvamuse et al., 2003; Garzón, 2007).
Desde el punto de vista analítico, los esfuerzos por entender el comportamiento de los sistemas de RD se han centrado en el estudio de la relación entre las bifurcaciones del espacio de parámetros y la formación de patrones. Desde esta perspectiva, se han estudiado los sistemas de RD mediante comparaciones de subsoluciones y supersoluciones, teoría de grado, índice de Conley, teoría de puntos críticos y perturbaciones singulares para varios tipos de máximos principales (Mei, 2000). Estos métodos han sido efectivos para el análisis de soluciones estacionarias y ondas viajeras (Sagués et al., 2004; Rüdiger et al., 2007). También se han estudiado escenarios de bifurcaciones complejas en sistemas de RD aplicando métodos de teoría de grupo para problemas con simetrías (Allgower y Georg, 1997; Painter, Othmer y Maini, 1999). Los esfuerzos en esta área del análisis matemático y, específicamente, de la dinámica de sistemas han permitido construir un gran conocimiento, que se ha comprobado y ampliado con el uso de la simulación numérica.
La simulación numérica de sistemas de RD ha permitido corroborar el conocimiento obtenido en forma analítica sobre la formación de patrones, como en Painter, Othmer y Maini (1999); Madzvamuse (2000); Painter, Maini y Othmer (2000) y Madzvamuse et al. (2003), donde se desarrollaron ejemplos numéricos sobre la formación de patrones en dominios bidimensionales bajo consideraciones de dominio creciente. En Madzvamuse (2000) se reporta la aparición de diferentes estructuras que pueden variar entre sistemas de bandas, puntos y combinaciones de estos patrones en dominios con decrecimiento exponencial. En Madzvamuse (2009) se reporta la formación de patrones en presencia de campos convectivos con divergencia nula. Es así como se ha dedicado un gran esfuerzo al estudio de los patrones de Turing bajo la deformación del dominio de la solución y cuando está sometido a campos de flujo.
Siguiendo un planteamiento similar al usado en Turing (1952) y en Lefèvre y Mangin (2002), se utiliza el modelo de reacción de Schnakenberg (Garzón, 2007) con parámetros en el espacio de Turing para simular la aparición de los patrones en superficies que tienen crecimiento; en especial, se han hecho ejemplos sobre esferas. Para la solución de las ecuaciones de reacción-difusión se presenta un método de solución en superficies en tres dimensiones mediante el método de los elementos finitos con el uso de la formulación lagrangiana total.
2. MATERIALES Y MÉTODOS
2.1 Sistema de reacción-difusión (RD)
Un sistema de reacción-difusión puede controlar la formación de los patrones siempre que sus parámetros reactivos y difusivos se encuentren en el espacio de Turing (Garzón, 2007). Para estudiar los patrones de Turing, se inicia con la definición de un sistema de reacción-difusión para dos especies, dado por:
donde u1 y u2 son las concentraciones de las especies químicas presentes en los términos de reacción f y g; d es el coeficiente de difusión adimensional y γ es una constante de adimensionalización del sistema.
En su libro de 1952 "The chemical basis of morphogenesis", Turing desarrolló las condiciones necesarias para la formación de patrones espaciales a partir de la ecuacion 1. Las condiciones para la formación de patrones determinan el espacio de Turing, dado por las siguientes restricciones:
donde f1 y g1 indican las derivadas de las funciones de reacción con respecto a las variables de concentración, por ejemplo  , (Garzón, 2007). Estas condiciones (2) están evaluadas en el punto de equilibrio que se obtiene haciendo f(u1, u2) = g(u1, u2) = 0.
, (Garzón, 2007). Estas condiciones (2) están evaluadas en el punto de equilibrio que se obtiene haciendo f(u1, u2) = g(u1, u2) = 0.
Las ecuaciones 1 y sus restricciones 2 permitieron el desarrollo de una rama de investigación de los sistemas dinámicos (Garzón, 2007): las inestabilidades de Turing. La teoría acerca de los patrones de Turing ha permitido explicar la formación de patrones biológicamente complejos, como las manchas que se encuentran en la piel de algunos animales (Madzvamuse et al., 2003; Madzvamuse, Wathen y Maini, 2003) y en problemas de morfogénesis (Gierer y Meinhardt, 1972), entre otros. Además, se ha comprobado de modo experimental que el comportamiento de algunos sistemas RD genera patrones de ondas viajeras y patrones espaciales estables (Kapral y Showalter, 1995; Maini, Painter y Chau, 1997; De Wit, 1999).
Las inecuaciones 2 contienen términos reactivos f(u1, u2) y g(u1, u2) que tienen una importante contribución en la formación de los patrones de Turing. En este artículo, las ecuaciones que se han utilizado para el término reactivo son las de Schnakenberg (Madzvamuse, 2000; Garzón, 2007), dadas por:
Donde a y b son parámetros adimensionales del modelo. Los puntos de estado estable están dados por  . Aplicando las restricciones 2 al modelo 1 en el punto de estado estable (u1, u2)0, se obtiene un conjunto de restricciones que permiten establecer el sitio geométrico de los parámetros en el espacio de Turing (Madzvamuse, 2000; Garzón, 2007).
. Aplicando las restricciones 2 al modelo 1 en el punto de estado estable (u1, u2)0, se obtiene un conjunto de restricciones que permiten establecer el sitio geométrico de los parámetros en el espacio de Turing (Madzvamuse, 2000; Garzón, 2007).
Haciendo uso del análisis de estabilidad lineal (Madzvamuse, 2000; Madzvamuse et al., 2003; Garzón, 2007), se pueden calcular los valores de los parámetros adimensionales d y γ, requeridos para la formación de patrones de Turing bajo el modelo de RD.
2.2 Deformación de las superficies
Para deformar la superficie donde se lleva a cabo la solución de las ecuaciones (1), se utilizaron las ideas sugeridas en Harrison, Wehner y Holloway (2002), Holloway y Harrison (2008) y Lefèvre y Mangin (2010), donde la superficie se deforma en función del tiempo y el espacio. Por tanto, la ecuación de deformación está dada por:
Donde h(x, y, z, t) es una función que determina la tasa de crecimiento.
Al incluirse el término de crecimiento de la superficie (ecuación 4), se modifican las ecuaciones 1, donde se presenta un nuevo término que tiene en cuenta la convección y la dilatación del dominio, dado por:
Donde el término nuevo div(uiv) incluye la convección y dilatación que se debe al crecimiento del dominio, dado por la velocidad.
Para solucionar el sistema de reacción-difusión-convección descrito en (5), se emplea el método de los elementos finitos (Hoffman, 1992; Belytschko, Liu y Moran, 2000; Holzapfel, 2000; Hughes, 2003), y el método de Newton-Raphson (Hoffman, 1992) para solucionar el sistema no lineal de ecuaciones diferenciales parciales que se derive de la formulación. La imposición del campo de crecimiento sobre la superficie se hace mediante la solución de la ecuación 4, con lo que se obtiene la nueva configuración (actual) y el campo de velocidades que se incluirá en el problema de RD. Para ver un análisis detallado, remitirse a Garzón-Alvarado, Martínez y Linero (2011).
2.3 Aplicación del campo de velocidades y solución computacional
Para calcular el movimiento de la malla y la velocidad a la cual se deforma el dominio se utiliza la ecuación 4, la cual se integra mediante el método de Euler:
Donde St+dt y St son la configuración de la superficie en el estado t y t+dt. Por tanto, la velocidad se obtiene mediante:
Donde el término de velocidad tiene dirección y magnitud que depende del punto material de la superficie S.
Adicionalmente, para resolver el sistema de ecuaciones resultantes por los métodos de los elementos finitos y de Newton-Raphson, se hizo un programa en Fortran y se solucionaron los varios ejemplos en un laptop de 4096 MB en RAM y 800 MHz de velocidad de procesador.
De otro lado, se ha utilizado una función lineal para el movimiento de los nodos, de tal forma que la ecuacion que rige el crecimiento está dada por la evolución del radio de la figura, así:
La figura 1 muestra el dominio sobre el cual se resuelven las ecuaciones de reacción-difusión-convección. En el caso de la solución sobre esferas (figura 1) se usan 6099 nodos y 12194 elementos.
3. EJEMPLOS DE APLICACIÓN Y RESULTADOS NUMÉRICOS
En las figuras 2 a 6 se muestran los resultados de la simulación numérica sobre esferas. Se usaron los siguientes parámetros del sistema de reacción-difusión de Schnakenberg: a = 0,1; b = 0,9; γ = 29,0 y d = 10,0. De modo específico, en la figura 2 la velocidad de crecimiento es nula, por tanto, se tiene la solución sobre un dominio fijo esférico. Por el contrario, en las figuras 3, 4, 5 y 6 se emplean valores de de 0,001; 0,01; 0,1 y 1,0, respectivamente. En el mismo orden de ideas se usan los siguientes valores de pasos de tiempo en cada simulación: 0,83; 0,083; 0,0083 y 0,00083 unidades de tiempo adimensional, respectivamente.
En la figura 2 se observa la evolución de los patrones en un dominio fijo. En t=5,0 se muestra la formación de un patrón con dos manchas en cada polo. Conforme transcurre el tiempo, se establece el patrón de tres puntos (manchas) y en t=15,0, el patrón final de estado estable. Con los mismos parámetros de reacción-difusión, en la figura 3, se utiliza la ecuación de crecimiento con una velocidad  de 0,001. En la figura 3b, se puede notar que la velocidad de crecimiento es suficientemente baja para la formación de un patrón estable, similar al que se genera en la figura 2. Conforme crece la esfera, las manchas y puntos se multiplican, aunque el tamaño de las manchas y puntos son iguales que los observados en instantes previos.
de 0,001. En la figura 3b, se puede notar que la velocidad de crecimiento es suficientemente baja para la formación de un patrón estable, similar al que se genera en la figura 2. Conforme crece la esfera, las manchas y puntos se multiplican, aunque el tamaño de las manchas y puntos son iguales que los observados en instantes previos.
En la figura 4 se usa  = 0,01. De nuevo, en la figura 4b, se observa la formación de un patrón similar al encontrado en el estado estable de la figura 2. Este patrón se instaura gracias a que la velocidad de crecimiento es baja. A medida que pasa el tiempo, se nota la formación de una mayor cantidad de manchas. En la figura 4g se pierden las manchas para formar bandas.
= 0,01. De nuevo, en la figura 4b, se observa la formación de un patrón similar al encontrado en el estado estable de la figura 2. Este patrón se instaura gracias a que la velocidad de crecimiento es baja. A medida que pasa el tiempo, se nota la formación de una mayor cantidad de manchas. En la figura 4g se pierden las manchas para formar bandas.
Con  = 0.1, en la figura 5, la velocidad de crecimiento no permite la instauración de las manchas de estado estable halladas en la figura 3. Por tanto, aparece un sistema complejo que mezcla manchas alargadas, bandas y puntos, como se observa en toda la simulación. En la figura 6, con
= 0.1, en la figura 5, la velocidad de crecimiento no permite la instauración de las manchas de estado estable halladas en la figura 3. Por tanto, aparece un sistema complejo que mezcla manchas alargadas, bandas y puntos, como se observa en toda la simulación. En la figura 6, con  = 1.0, no se forman patrones de Turing. En este caso el término convectivo domina a los términos difusivo y reactivo, por lo que se pierde la distribución de patrones de Turing.
= 1.0, no se forman patrones de Turing. En este caso el término convectivo domina a los términos difusivo y reactivo, por lo que se pierde la distribución de patrones de Turing.
4. DISCUSIÓN Y CONCLUSIONES
En este artículo se recurrió al método de los elementos finitos para solucionar un sistema de ecuaciones de reacción-difusión de carácter no lineal. Para estudiar la versatilidad del método se desarrollaron varios ejemplos de reacción-difusión, con un sistema reactivo del tipo Schnakenberg. El sistema no lineal se resolvió por el método de Newton-Raphson. Los parámetros del modelo cumplen las restricciones del espacio de Turing, por tanto, los patrones que se obtienen en la solución exhiben inestabilidades espaciales denominadas de Turing.
En este trabajo se logró modelar la deformación de superficies en donde se desarrolla el proceso de reacción y difusión, similar a lo que ocurriría, por ejemplo, en la piel de un animal, donde un proceso reactivo permite la formación de manchas características de algunas especies. Para este fin se utilizó la formulación de mecánica de medio continuo, que permite aproximar la solución mediante un esquema lagrangiano total. En este método se usó la configuración de referencia o indeformada (Babuška et al., 1995) para llevar a cabo los cálculos numéricos en cada instante. Esta formulación permite generalizar la metodología propuesta por Madzvamuse et al. (2003) y Madzvamuse, Wathen y Maini (2003), donde se desarrolla un modelo de movimiento de malla para problemas bidimensionales planos. En este artículo se logra ampliar dicha formulación para cualquier movimiento espacial de una superficie en deformación.
REFERENCIAS
Allgower, Eugene L. and Georg, Kurt. Numerical path following. In: Handbook of Numerical Analysis, 1997, vol. 5, pp. 3-207. [ Links ]
Ardes, M.; Busse, F. and Wicht, J. (1997). "Thermal convection in rotating spherical shells". Physics of the Earth and Planetary Interiors, vol. 99, No. 1-2 (January), pp. 55-67. [ Links ]
Babuska, Ivo; Ihlenburg, Frank; Paik, Ellen T. and Sauter, Stefan A. (1995). "A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution". Computer Methods in Applied Mechanics and Engineering, vol. 128, No. 3-4 (December), pp. 325-359. [ Links ]
Belytschko, T.; Liu, W. K. and Moran, B. Nonlinear finite elements for continua and structures. John Wiley and Sons, 2000. [ Links ]
De Wit, A. (1999). "Spatial patterns and spatiotemporal dynamics in chemical systems". Advances in Chemical Physics, vol. 109, pp. 435-513. [ Links ]
Garzón, D. Simulación de procesos de reacción-difusión: Aplicación a la morfogénesis del tejido óseo. Tesis de Doctorado (Biomecánica Computacional). Universidad de Zaragoza, 2007. [ Links ]
Garzón-Alvarado, D. A.; Martínez, A. M. and Linero, D. (2011). "A model of cerebral cortex formation during fetal development using reaction-diffusion-convection equations with Turing space parameters". Comput Methods Programs Biomed, vol. 104, No. 3 (December), pp. 489-497. [ Links ]
Gierer, A. and Meinhardt, H. (1972). "A theory of biological pattern formation". Kybernetik, vol. 12, No. 1 (December), pp. 30-39. [ Links ]
Harrison, L. G.; Wehner, S. and Holloway, D. M. (2002). "Complex morphogenesis of surfaces: Theory and experiment on coupling of reaction-diffusion patterning to growth". Faraday Discussions, vol. 120, pp. 277-293. [ Links ]
Hirayama, O. and Takaki, R. (1988). "Thermal convection of a fluid with temperature-dependent viscosity". Fluid Dynamics Research, vol. 12, No. 1, pp. 35-47. [ Links ]
Hoffman, J. O. Numerical methods for engineers and scientists. New York, NY: McGraw-Hill, 1992. 823 p. [ Links ]
Holloway, David M. and Harrison Lionel G. (2008). "Pattern selection in plants: Coupling chemical dynamics to surface growth in three dimensions". Annals of Botany, vol. 101, No. 3, pp. 361-374. [ Links ]
Holzapfel, G. A. Nonlinear solid mechanics: A continuum approach for Engineering. John Wiley and Sons, 2000. [ Links ]
Hughes, T. J. R. The finite element method: Linear static and dynamic finite element analysis. New York: Courier Dover, 2003. [ Links ]
Kapral, Raymond and Showalter, Kenneth (eds). Chemical waves and patterns. Dordrecht: Kluwer, 1995. [ Links ]
Lefèvre, Julien and Mangin, Jean-François (2010). "A reaction-diffusion model of human brain development". PLoS Computational Biology, vol. 6, No. 4 (April), pp. 1-10. [ Links ]
Madzvamuse, Anotida. A numerical approach to the study of spatial pattern formation. Ph.D. thesis. Oxford University, UK, 2000. [ Links ]
Madzvamuse, Anotida; Thomas, Roger D. K.; Maini, Philip and Wathen, Andrew J. (2002). "A numerical approach to the study of spatial pattern formation in the ligaments of arcoid bivalves". Bulletin of Mathematical Biology, vol. 64, No. 3, pp. 501-530. [ Links ]
Madzvamuse, Anotida. (2009). "Turing instability conditions for growing domains with divergence free mesh velocity". Nonlinear Analysis: Theory, Methods and Applications, vol. 71, No. 12 (December), pp. 2250-2257. [ Links ]
Madzvamuse, Anotida; Sekimura, Toshio; Thomas, Roger D. K.; Wathen, Andrew J. and Maini, Philip K. The moving grid finite element method applied to biological problems. In: Morphogenesis and pattern formation in biological systems: Experiments and models. Tokyo: Springer, 2003, pp. 59-65. [ Links ]
Madzvamuse, Anotida; Wathen, Andrew J. and Maini, Philip K. (2003). "A moving grid finite element method applied to a model biological pattern generator". Journal of Computational Physics, vol. 190, pp. 478-500. [ Links ]
Maini, Philip K.; Painter, Kevin J. and Chau, H. N. P. (1997). "Spatial pattern formation in chemical and biological systems". Journal of the Chemical Society, Faraday Transactions, vol. 93, No. 20, pp. 3601-3610. [ Links ]
Mei, Z. Numerical bifurcation analysis for reaction-diffusion equations. Berlin/Heidelberg: Springer, 2000. [ Links ]
Painter, Kevin J.; Maini, Philip K. and Othmer, H. G. (2000). "A chemotactic model for the advance and retreat of the primitive streak in avian development". Bulletin of Mathematical Biology, vol. 62, pp. 501-525. [ Links ]
Painter, Kevin J.; Othmer, H. G. and Maini, Philip K. (1999) "Stripe formation in juvenile Pomacanthus via chemotactic response to a reaction diffusion mechanism". Proceedings of National Academy Sciences USA, vol. 96, No. 10 (May), pp. 5549-5554, 1999. [ Links ]
Rüdiger, Sten; Nicola, Ernesto M.; Casademunt, Jaume and Kramer, Lorenz (2007). "Theory of pattern forming systems under traveling-wave forcing". Physics Reports, vol. 447, No. 3-6 (August), pp. 73-111. [ Links ]
Sagués, Francesc; Míguez, David G.; Nicola, Ernesto M.; Muñuzuri, Alberto P.; Casademunt, Jaume and Kramer, Lorenz (2004). "Travelling-stripe forcing of Turing patterns". Physica D: Nonlinear Phenomena, vol. 199, No. 1-2 (December), pp. 235-242. [ Links ]
Turing, A. (1952). "The chemical basis of morphogenesis". Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, vol. 237, No. 641 (August), pp. 37-72. [ Links ]