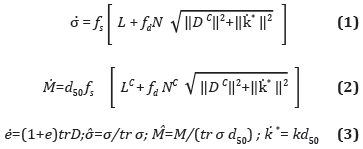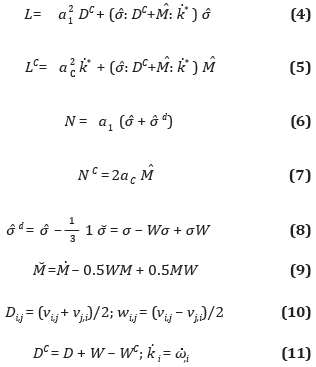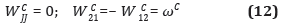Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.23 Envigado June 2015
DESEMPEÑO DEL CONTINUO DE COSSERAT PARA TENER EN CUENTA EFECTOS DE ESCALA EN UN ENSAYO DE CORTE DIRECTO
PERFORMANCE OF THE COSSERAT CONTINUUM IN ORDER TO TAKE INTO ACCOUNT THE SCALE EFFECTS IN A SHEAR DIRECT TEST
DESEMPENHO DO CONTÍNUO DE COSSERAT PARA CONSIDERAR OS EFEITOS DE ESCALA EM UM TESTE DE CISALHAMENTO DIRETO
Alfonso Mariano Ramos Cañón1, Luis Felipe Prada Sarmiento2
1 Ingeniero civil Pontificia Universidad Javeriana. MCs en Ingeniería Civil-Geotecnia Universidad Nacional de Colombia. PhD. En Ingeniería Universidad de los Andes. Pontificia Universidad Javeriana: Cra 7 No 42-27 Piso 7, Bogotá, Colombia. Teléfono: 57 + 1 + 3208230 ext. 6545. Correo electrónico: a-ramos@javeriana.edu.co.
2 Ingeniero civil Pontificia Universidad Javeriana. MCs en Ingeniería Civil-Recursos Hídricos Universidad de los Andes. PhD (c). en Ingeniería Universidad de los Andes.
Artículo recibido: 30-IV-2014 / Aprobado: 26-II-2015
Disponible online: 30 de junio de 2015
Discusión abierta hasta junio de 2016
RESUMEN
Los resultados del ensayo de corte directo tanto a nivel experimental como en simulaciones con elementos discretos se ven afectados por la escala, es decir los resultados dependen del tamaño de las partículas y de la caja de corte. El geotecnista tiene que utilizar los resultados de los ensayos de laboratorio a escala pequeña en problemas a escala natural. En este trabajo se implementa en elementos finitos el modelo constitutivo hipoplástico basado en el continuo de Cosserat y se muestra la capacidad de simular algunos de los efectos asociados con el tamaño de escala por la introducción de una longitud característica. El continuo de Cosserat introduce la rotación como cuerpo rígido de los elementos como grado de libertad adicional al continuo convencional presentando asimetría en el tensor de esfuerzos. Se encuentra que 1. El material desarrolla mayor rigidez inicial y alcanza más rápido la resistencia pico en cajas de corte pequeñas o en materiales cuyas partículas son más grandes. 2. La resistencia residual no depende del tamaño de la caja ni del tamaño de partícula, y 3. Se subestima el ángulo de fricción pico cuando se calcula con medidas en el contorno comparadas con las obtenidas en la zona de corte.
PALABRAS CLAVE: Continuo de Cosserat; elementos finitos; ensayo de corte directo; continuo de Boltzmann.
ABSTRACT
Results of the direct shear test performed both experimentally and numerical simulations using the discrete element method are affected by the scale, i.e. results depend on both, the particle size and the size of the shear box. The geotechnical engineer must use the results of tests on small-scale laboratory in solve real scale problems. This work shows the implementation in finite element method of the hypoplastic constitutive model based on the Cosserat continuum and its ability to simulate some of the effects associated with the size scale by the introduction of a characteristic length is demonstrated. The Cosserat continuum introduced the rotation as a rigid body of the elements as an additional degree of freedom to conventional continuous and presents asymmetry stress tensor. From the analysis it is found that 1. The material develops higher initial stiffness and reaches peak strength faster in small boxes or in materials whose particles are larger. 2. The residual strength does not depend on the size of the shear box and particle size 3. Peak friction angle is underestimated when calculated with the contour measures compared with those obtained in the cutting zone.
KEY WORDS: Cosserat Continuum; Finite Element Method; Shear Direct Test; Boltzmann Continuum.
RESUMO
Os resultados do ensaio de cisalhamento direto tanto experimental como em simulações com elementos discretos se vem afetados pela escala, ou seja, os resultados dependem do tamanho das partículas e da caixa do cortador. O Geotecnista tem que usar os resultados dos testes de laboratório em pequena escala em problemas de escala natural. Neste trabalho, usa-se em elementos finitos o modelo constitutivo hipoplásico baseado no contínuo de Cosserat e se mostra a capacidade de simular alguns dos efeitos associados com o tamanho da escala através da introdução de um comprimento característico. O Contínuo Cosserat introduze a rotação como corpo rígido dos elementos como grau de liberdade adicional ao contínuo convencional apresentando assimetria no tensor de stress. Encontra-se que 1. O material desenvolve uma maior rigidez inicial e atinge mais rápido a resistência pico em pequenas caixas ou materiais de corte cujas partículas são maiores. 2. A resistência residual não depende do tamanho da embalagem e do tamanho de partícula, e 3. O ângulo de atrito pico é subestimado quando as medidas são calculadas no contorno comparadas com aquelas obtidas na zona de corte.
PALAVRAS-CHAVE: Continuo de Cosserat; Elementos Finitos; Teste de cisalhamento direito; Continuo de Boltzmann.
1. INTRODUCCIÓN
El problema del efecto del tamaño es particularmente importante para el investigador geotécnico ya que inevitablemente debe extrapolar los resultados de las pruebas de laboratorio a escala reducida a estructuras reales (Bazant y Xiang, 1997). El ensayo de corte directo ha sido uno de los más usados en la práctica de la ingeniería geotécnica para estimar resistencia pico y residual debido principalmente a la facilidad en su ejecución y a su buena repetibilidad (Bareither, 2008). Sin embargo también ha sido objeto de múltiples críticas debido a las dificultades que tiene la interpretación de los resultados (Wu, et al., 2008). Tanto a nivel experimental como en simulaciones con el método de elementos discretos (DEM) se ha encontrado que en ensayos de corte directo el tamaño de la caja de corte y el tamaño de las partículas afectan los resultados (Ceratto y Lutenegger, 2006; Orlando, et al., 2009; Zhou, et al., 2009; Wu, et al., 2008; Palmeira y Milligan,1989; Gao, et al., 2000). En este trabajo se realizan simulaciones con el método de elementos finitos (FEM) de ensayos de corte directo con el modelo constitutivo hipoplástico polar (continuo de Cosserat) con el objetivo de investigar su desempeño en la simulación de los efectos de escala en el corte directo basado en comparaciones de modelaciones en DEM y en ensayos de laboratorio, realizados en otros estudios. El continuo de Cosserat introduce una longitud característica que permite regularizar el problema de valor de contorno garantizando que las ecuaciones diferenciales permanezcan bien condicionadas. La principal diferencia entre el continuo de Cosserat y el convencional es que en el primero se aplica el principio de acción local en el sentido de Noll (Romano, et al., 2004), es decir los procesos que suceden en un punto material de un cuerpo dependen únicamente de ese mismo punto material y no de los adyacentes al mismo. Del análisis de los resultados de la implementación en elementos finitos del modelo constitutivo hipoplástico en el medio continuo de Cosserat: a) se obtiene el tamaño mínimo de los elementos finitos cuadriláteros de forma tal que los resultados no son dependientes de la malla, b) se demuestra que el tamaño de la caja de corte afecta la rigidez global del material c) se observa que la resistencia residual es independiente del tamaño de la caja de corte y finalmente d) se evidencia que el ángulo de fricción pico se subestima cuando se calcula con medidas en el contorno comparadas con las desarrolladas en la zona de corte.
2. METODOLOGÍA
Los pasos metodológicos usados para desarrollar el presente trabajo fueron los siguientes: a) Selección del modelo constitutivo capaz de simular el comportamiento en arenas (numeral 2.1). b) Determinación de las funciones de forma para elementos finitos cuadriláteros en deformación plana con los grados de libertad adicionales del continuo de Cosserat. c) Implementación numérica en elementos finitos del medio continuo de Cosserat y del modelo constitutivo de hipoplasticidad polar en el lenguaje de programación fortran. d) Determinación e implementación del problema de valor de contorno y de las condiciones de frontera para el ensayo de corte directo (numeral 2.2). e) Los resultados y análisis se presentan en la sección 3.
2.1 Modelo constitutivo
El ensayo de corte directo tiene efectos asociados con la escala (Ceratto y Lutenegger, 2006; Orlando, et al., 2009; Zhou, et al., 2009; Wu, et al. (2008); Palmeira y Milligan,1989; Gao, et al., 2000). En mecánica del medio continuo se deben introducir estos efectos cuando las partículas son grandes en comparación con las dimensiones del contorno del problema y/o comparadas con las superficies donde se aplica la carga. En este caso, las cargas puntuales y superficiales generan momentos y microrotaciones (Eringen 1968). Una de las posibilidades para tener en cuenta dichos efectos de escala en FEM es a través del continuo de Cosserat. El continuo de Cosserat presenta en su formulación una longitud inherente que permite escalar el problema, adicionalmente introduce los grados de libertad de rotación, que no aparecen en el continuo convencional. La hipoplasticidad basada en el continuo de Cosserat o hipoplasticidad polar tiene en su formulación el diámetro medio de la partícula d50 como longitud característica. La evolución del tensor de esfuerzos no simétrico de Cauchy y el tensor de esfuerzos acoplado es descrita por funciones tensoriales no lineales. La representación tensorial de la hipoplasticidad polar se puede resumir así (Tejchman y Bauer,1996; Tejchman, 1997):
donde 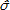 es el tensor de esfuerzos normalizado,
es el tensor de esfuerzos normalizado, 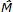 es el tensor de esfuerzos acoplado normalizado,
es el tensor de esfuerzos acoplado normalizado, 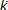 * es la tasa del tensor de microcurvatura escalada y d50 es el diámetro medio del grano que es usado como una longitud característica para materiales granulares. Huang (2000) propone la siguiente representación de los tensores, L, N, LC y NC, y de la Ecuación 1
* es la tasa del tensor de microcurvatura escalada y d50 es el diámetro medio del grano que es usado como una longitud característica para materiales granulares. Huang (2000) propone la siguiente representación de los tensores, L, N, LC y NC, y de la Ecuación 1
Para condiciones de deformación plana, los componentes del tensor de tasa de rotación de Cosserat son:
Los demás argumentos de las ecuaciones 1 y 2 son (Huang, 2000; Tejchman, 2005)
En donde σ es el tensor de esfuerzos de Cauchy, 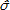 d es la parte desviadora de σ,
d es la parte desviadora de σ, 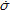 es la tasa del tensor de incremento de esfuerzos objetivo de Jaumann,
es la tasa del tensor de incremento de esfuerzos objetivo de Jaumann, 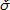 es el tensor de incremento de esfuerzo,
es el tensor de incremento de esfuerzo, 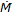 es el tensor de esfuerzo acoplado objetivo de Jaumann,
es el tensor de esfuerzo acoplado objetivo de Jaumann, 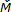 es el tensor de incremento de esfuerzo acoplado, e es la relación de vacíos actual, D = Dij es el tensor de tasa de deformación, W = Wij es el tensor spin, WC es el tensor de incremento de rotaciones de Cosserat, k es el tensor de microcurvatura de Cosserat. En el caso de deformación plana, el tensor de tasa de rotación de Cosserat tiene un solo componente independiente ωC, DC es el tensor de tasa de deformación de Cosserat, 1 es el tensor unitario de segundo orden, fs es el factor de rigidez, hs es la dureza granular, fd es un factor de densidad, aC es una constante micropolar, eC es la relación de vacíos crítica, eC0 es el valor de eC para un esfuerzo medio igual a cero, ed es la relación de vacíos más densa, ed0 es el valor de ed para esfuerzo medio igual a cero, ei es la relación de vacíos máxima, ei0 es el valor de ei para esfuerzo medio igual a cero, α es el coeficiente de picnotropía, n es el coeficiente de compresión, β es el coeficiente de rigidez, a1 es un parámetro que representa la parte desviatórica del esfuerzo normalizado en el estado crítico, φC ángulo de fricción crítico y θ es el ángulo de Lode. Bajo condiciones de deformación plana y a diferencia del continuo convencional que solo tiene dos grados de libertad traslacionales, un punto material en el continuo de Cosserat tiene 3 grados de libertad, dos de traslación y uno de rotación, u1, u2 y ωC respectivamente (Figura 1).
es el tensor de incremento de esfuerzo acoplado, e es la relación de vacíos actual, D = Dij es el tensor de tasa de deformación, W = Wij es el tensor spin, WC es el tensor de incremento de rotaciones de Cosserat, k es el tensor de microcurvatura de Cosserat. En el caso de deformación plana, el tensor de tasa de rotación de Cosserat tiene un solo componente independiente ωC, DC es el tensor de tasa de deformación de Cosserat, 1 es el tensor unitario de segundo orden, fs es el factor de rigidez, hs es la dureza granular, fd es un factor de densidad, aC es una constante micropolar, eC es la relación de vacíos crítica, eC0 es el valor de eC para un esfuerzo medio igual a cero, ed es la relación de vacíos más densa, ed0 es el valor de ed para esfuerzo medio igual a cero, ei es la relación de vacíos máxima, ei0 es el valor de ei para esfuerzo medio igual a cero, α es el coeficiente de picnotropía, n es el coeficiente de compresión, β es el coeficiente de rigidez, a1 es un parámetro que representa la parte desviatórica del esfuerzo normalizado en el estado crítico, φC ángulo de fricción crítico y θ es el ángulo de Lode. Bajo condiciones de deformación plana y a diferencia del continuo convencional que solo tiene dos grados de libertad traslacionales, un punto material en el continuo de Cosserat tiene 3 grados de libertad, dos de traslación y uno de rotación, u1, u2 y ωC respectivamente (Figura 1).
El tensor de tasa de deformación de Cosserat t iene cuatro componentes diferentes de cero 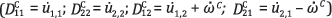 . El tensor de esfuerzos tiene cinco componentes diferentes de cero (σ11, σ22, σ33, σ12; σ21). El tensor de microcurvatura y el tensor de esfuerzos acoplados tiene cuatro componentes diferentes de cero
. El tensor de esfuerzos tiene cinco componentes diferentes de cero (σ11, σ22, σ33, σ12; σ21). El tensor de microcurvatura y el tensor de esfuerzos acoplados tiene cuatro componentes diferentes de cero  .
.
El procedimiento detallado para la determinación de los parámetros es explicado por Herle y Gudehus (1999). Los parámetros de la arena de Karlsruhe fueron tomados de Herle, 1998).
2.2 Condiciones iniciales y de contorno
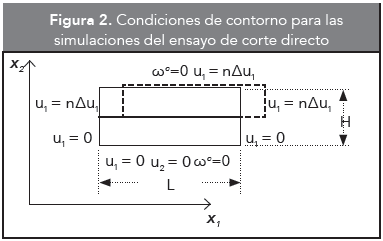
Inicialmente las simulaciones del corte directo se realizaron en una caja de arena de 25 mm de altura (H) y 60 mm de base (L). Las condiciones cinemáticas simula la caja de corte tipo Skempton y Bishop (1950) (Figura 2) y se explican a continuación: a. se impone una carga uniforme en la placa superior de la muestra equivalente a la transmisión de un esfuerzo constante σC, b. se supone la parte inferior de la muestra muy rugosa (u1 = 0, u2 = 0, ωC = 0), al igual que el contorno superior ωC = 0, c. la parte inferior de los contornos laterales de la muestra se restringe en sentido horizontal u1 = 0 y d. se prescribe un desplazamiento horizontal u1 = nΔu1 a todos los nodos de los contornos laterales superiores (n es el número del paso).
El máximo desplazamiento horizontal fue de u1/H = 0,24 Los incrementos de desplazamiento horizontal fueron menores a Δu1/H = 0,00005. El estado inicial de esfuerzos se supone sin cantidades polares y con un estado Ko generado por la carga en la placa superior.
3. RESULTADOS
3.1 Influencia del tamaño de los elementos finitos
Se realizaron simulaciones de tres mallas de elementos finitos cuadriláteros variando el tamaño de la base y la altura de cada elemento finito: a) 0,005m x 0,005m equivalente a 10d50 x 10d50, b) 0,005m x 0,0022m equivalente a 10 d50 x 4,5 d50 c) 0,005m x 0,0022m equivalente a 5d50 x 4,5 d50. La Figura 3 muestra la evolución de las rotaciones de Cosserat para los tres enmallados al comienzo de la etapa de corte (Figura 3a u/H = 0,012), cercano al pico de fuerza global T (Figura 3b u/H = 0,04) y a muy grandes desplazamientos (Figura 3c u/H = 0,24) en función de la altura (H) en un corte vertical en la mitad de la muestra. La fuerza cortante global T es la suma de todas las fuerzas nodales a lo largo de la placa superior y a lo largo de los contornos laterales (Masson y Martínez, 2001).
Se observa que para desplazamientos pequeños (Figura 3a) la rotación de Cosserat c no presenta diferencias notables en función de los diferentes tamaños de los elementos y las rotaciones de Cosserat son pequeñas a lo largo de toda la altura de la muestra. A medida que aumenta el desplazamiento horizontal de la caja superior y cercano al pico en la fuerza cortante global (Figura 3b), se presenta un fuerte incremento en las rotaciones de Cosserat, siendo más grande en la mitad de la muestra, además se presentan algunas diferencias debido a los tamaños de elementos. Para grandes desplazamientos horizontales (Figura 3c) se generan mayores rotaciones de Cosserat principalmente en la zona media de la muestra (zona de corte), sin embargo la mayor tasa de incrementos de las rotaciones de Cosserat se presentan hasta alcanzar el pico en la resistencia. Los incrementos de la rotación de Cosserat desde desplazamientos horizontales cercanos al pico de esfuerzos hasta altos desplazamientos horizontales se incrementan en una tasa mucho menor. Es decir, la mayoría de rotaciones de Cosserat se presentan desde el inicio de la etapa de corte hasta que se presenta el pico en la fuerza global de corte T. Las rotaciones de Cosserat no presentan un salto abrupto dentro de la zona de corte, sino que varían con gradiente a lo largo de la altura de la muestra, situación similar a la que se encuentra en modelaciones en DEM para las rotaciones de las partículas (Masson y Martínez, 2001).
La Figura 4 presenta la evolución de la relación de vacíos con el desplazamiento normalizado para los tres tamaños de elementos en tres elementos en un corte vertical en la mitad de la muestra. La ubicación de los elementos en el corte vertical son: en la base de la muestra, en la zona de corte y en la parte superior de la muestra para una relación de vacíos inicial e0 = 0,7.
Se presenta un fuerte incremento en la relación de vacíos (dilatancia) dentro de la zona de corte, en tanto que en la parte inferior y superior de la muestra se presenta una leve disminución en la relación de vacíos comparado con la relación de vacíos inicial. Se observa que no se presentan diferencias entre los enmallados 10d50 x 4,5d50 (Figura 4b) y 5d50 x 4,5d50 (Figura 4c). En cambio se observa diferencias apreciables entre la malla 10d50 x 10d50 y las otras dos.
De acuerdo a los resultados obtenidos, en términos generales se observa que no hay diferencias apreciables en los resultados cuando se usan elementos del tamaño 10d50 x 4,5d50 y 5d50 x 4,5d50, razón por lo que en adelante se usarán elementos cuyas dimensiones máximas sean menores a 10d50 x 4,5d50 con lo que computacionalmente los resultados serán más eficientes (en términos de tiempo) sin afectar su confiabilidad. Tejchman (1997) mostró que los resultados son independientes para hipoplasticidad polar siempre y cuando el tamaño de los elementos triangulares sea menor a 5d50. Resultado similar al encontrado para elementos cuadriláteros en este trabajo.
3.2 Influencia del tamaño de la muestra
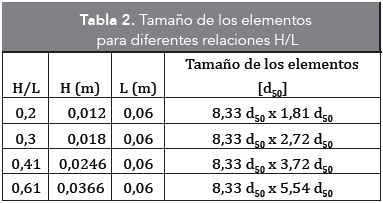
Para estudiar la influencia del tamaño de la muestra en un ensayo de corte directo, se simuló cuatro diferentes tamaños de caja de corte. Las dimensiones de la caja de corte varían en función de la relación de aspecto H/L así: 0,2; 0,3; 0,41 y 0,61, donde H es la altura de la caja de corte y L es la base. El esfuerzo normal de la muestra es σc = 100 kPa y la relación de vacíos eo = 0,75 que permite que la muestra tenga un comportamiento de ablandamiento por deformación en la etapa de carga. Se mantuvo constante la base de L de la caja de corte en 0,06 m. Las dimensiones de los elementos en función de d50 para cada relación H/L se muestran en la Tabla 2. En todos los casos se procuró que el tamaño de los elementos sea menor a 10d50 x 4,5d50, a excepción de H/L = 0,61.
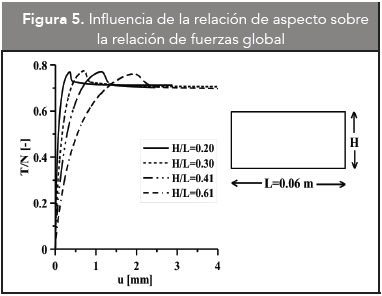
En la Figura 5 se observa que la relación de fuerzas global T/N desarrolladas para un mismo nivel de desplazamiento horizontal es menor a medida que las dimensiones de la caja de corte se incrementan para desplazamientos pequeños. Resultado concordante con lo reportado por Cerato y Luteneger (2006) para distintos tipos de arena y de tamaños de caja. Cerato y Luteneger (2006) explican que tal comportamiento puede deberse a que en cajas de corte pequeñas, la propagación de la zona de corte está restringida. Además se observa que se presenta mayor rigidéz para partículas más grandes, concordante con modelaciones en DEM reportadas por Zhou, et. al. (2009). Wu, et. al., 2008 realizaron ensayos de corte directo con diferentes secciones transversales de la arena de Toyoura y encontraron que la resistencia residual es independiente del tamaño del espécimen, lo que se observa claramente en la Figura 5. Sin embargo también reportaron que la resistencia pico disminuye con el incremento en la sección transversal del espécimen, situación que hipoplasticidad polar no pudo modelar. Xuebin, et al., (2004) utilizando elastoplasticidad con gradiente en simulaciones de FEM para rocas reportan que los especímenes pequeños tiene mayor rigidez antes de la falla, situación concordante con los resultados mostrados en la Figura 5. Es de anotar que la elastoplasticidad con gradiente introduce una longitud característica en el análisis que permite regularizar el problema de valor de contorno de manera semejante a lo que se realiza usando el continuo de Cosserat.
3.3 Diferencias entre el ángulo de fricción movilizado en la zona de corte (local) y el calculado con mediciones globales
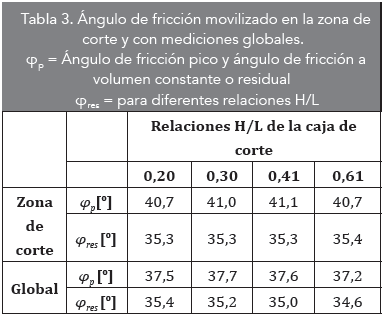
En la práctica normal de la geotecnia, el ángulo de fricción se calcula a partir de las mediciones globales de la caja de corte. En dichos cálculos se supone que la zona de falla es horizontal con distribución uniforme de esfuerzos para desplazamientos cercanos al esfuerzo pico, situación que ha sido comprobada alejada de lo que se ve en el experimento. Por otro lado, se denomina el ángulo de fricción local a aquel que se obtiene del seguimiento del estado de esfuerzos al interior de la muestra en la zona de corte (Zhang y Thornton, 2007). Dado lo anterior, la medición local no se puede obtener de los ensayos de laboratorio. En la Tabla 3 se presenta el ángulo de fricción movilizado tanto pico φp como residual φres para cajas de corte con diferente relación de aspecto H/L calculadas en la zona de corte y con mediciones globales. Se presentan diferencias en el ángulo de fricción movilizado si se comparan las medidas globales con medidas locales. Medida global es a partir de las reacciones y medida local es a partir de las mediciones de los esfuerzos dentro de la zona de corte.
El ángulo de fricción movilizado pico φp en la zona de corte es 8 % mayor que el ángulo de fricción con mediciones globales, independiente de la relación de aspecto. El ángulo de fricción residual φres es casi constante tanto para la zona de corte como el que se encuentra en mediciones globales independientes de la relación de aspecto. La diferencia entre los valores de φp se puede deber a que el esfuerzo normal es menor en la zona de corte que el que se aplica en la parte superior de la muestra debido a la fricción desarrollada en las paredes. Para la medición del ángulo de fricción residual, la zona de corte ya está totalmente desarrollada y puede decirse que es horizontal con esfuerzos homogéneos. Variaciones entre el ángulo de fricción movilizado en la zona de corte y el que se calcula con mediciones globales son reportadas por Zhang y Thornton (2007) con DEM.
Es importante determinar la relación que existe entre las diferentes longitudes que se encuentran inmersas en la implementación numérica del método de elementos finitos basado en el continuo de Cosserat. El tamaño de la caja de corte determina una longitud máxima de control en el problema de valor de contorno. Autores como Ramos y Lizcano (2010), Maier (2004), De Boerst, et al. (1993) han mostrado que el tamaño característico del elemento finito debe ser lo suficientemente pequeño para que los resultados no dependan de la discretización del método, tema abarcado en el numeral 3.1. Allí se muestra que para el continuo de Cosserat usando un modelo constitutivo hipoplástico, el tamaño del elemento no puede ser más grande que 10d50 x 4,5d50 para que los resultados no tengan dependencia del tamaño del elemento, es decir el continuo de Cosserat sirve como una técnica de regularización de los resultados. Dentro de la formulación del continuo de Cosserat es necesario trabajar con una longitud característica que determina, entre otros, los tensores de microcurvatura (Ecuación 3). Para materiales granulares se ha tomado típicamente como el d50. (Tamaño de grano cuyo 50 % del material es mayor), es decir la longitud característica es el mismo tamaño de la partícula d50.
Por lo tanto se observa que en el continuo de Cosserat, el tamaño característico de la partícula, el tamaño del elemento y el tamaño de la caja de corte (longitud del problema de valor de contorno) son siempre dependientes. Situación que no se presenta en el continuo convencional.
4. CONCLUSIONES
La introducción de una longitud característica permite escalar el problema de valor de contorno en el modelo constitutivo hipoplástico con lo que algunos efectos de escala encontrados en ensayos de laboratorio y en DEM fueron adecuadamente modelados. La introducción de la longitud característica se realizó a través de la implementación en FEM de la hipoplasticidad en el continuo de Cosserat. Adicional a la posibilidad de tener en cuenta los efectos de tamaño en los resultados, se incorpora el grado de libertad de rotación, que el continuo convencional no lo tiene. Del trabajo se concluye lo siguiente:
El tamaño mínimo de los elementos finitos cuadrilateros en hipoplasticidad polar deben ser menores a 10d50 x 5d50 para que los resultados sean independientes de la malla usada.
El material desarrolla mayor rigidez y alcanza la resistencia pico más pronto en una caja de corte pequeña o con materiales cuyas partículas sean más grandes.
La resistencia residual es independiente del tamaño de la caja de corte.
Hay una subestimación del ángulo de fricción pico desarrollado cuando se calcula con medidas en el contorno comparadas con las desarrolladas en la zona de corte.
Notación
La notación usada en el presente documento se resume de la siguiente forma: Las letras en mayúscula indican tensores de segundo orden (DC), las letras en mayúscula y subrayadas indican tensores de cuarto orden (L), tr( ) extrae la traza del tensor, las cursivas son escalares (α, β), un punto sobre las letras indican derivada con respecto al tiempo, (
) extrae la traza del tensor, las cursivas son escalares (α, β), un punto sobre las letras indican derivada con respecto al tiempo, ( , j) indica la derivada con respecto a la posición xj. La operación (:) entre tensores de segundo orden indican doble contracción, que en notación indicial es c = A: B = AijBij donde c es un escalar. El signo de la multiplicación entre tensores es omitido y la operación con notación indicial es C = AB = AijBjk = Bik.
, j) indica la derivada con respecto a la posición xj. La operación (:) entre tensores de segundo orden indican doble contracción, que en notación indicial es c = A: B = AijBij donde c es un escalar. El signo de la multiplicación entre tensores es omitido y la operación con notación indicial es C = AB = AijBjk = Bik.
5. FINANCIAMIENTO
Los autores agradecen a la Pontificia Universidad Javeriana por la financiación del presente trabajo a través del proyecto 4709 «inestabilidad en materiales granulares».
REFERENCIAS
Bareither, C.; Benson, C.; Edil, T. (2008). Reproducibility of Direct Shear Tests Conducted on Granular Backfill Materials. Geotechnical Testing Journal, 31 (1), pp. 1-11. [ Links ]
Bazant, Z.; Xiang, Y. (1997). Size Effect in Compression Fracture: Splitting Crack Band Propagation. Journal of Engineering Mechanics. ASCE 123 (2), 162-172. [ Links ]
Cerato, A.; Lutenegger, A. J. (2006). Specimen Size and Scale Effects of Direct Shear Box Test of Sands. Geotechnical Testing Journal, 29 (6). [ Links ]
De Boerst, R.; Sluys. L.; Mulhaus, H.; Pamin, J. (1993). Fundamental Issues in Finite Element Analysis of Localization of Deformation. Engineering Computations. 10, pp. 99-121. [ Links ]
Eringen, A. (1968). Fracture, volume II - Mathematical Fundamentals, Chapter Theory of Micropolar Elasticity. pp. 621-729. Academic Press. London. [ Links ]
Gao, J.; Haixue, Y.; Weibing, Z. (2000). Characteristic Study of Interface Between Soil and Concrete by Using Larger Size Single Shear Apparatus and Numerical Analysis. China Civil Engineering Journal, 33 (4), pp. 42-46. [ Links ]
Herle, I. (1998). A Relation Between Parameters of a Hypoplastic Constitutive Model and Grain Properties. In Localization and Bifurcation Theory for Soils and Rocks. Adachi, T., Oka, K., Yashima, A. (eds) Balkema, pp. 91-98. [ Links ]
Herle, I.; Gudehus, G. (1999). Determination of Parameters of a Hypoplastic Constitutive Model from Properties of Grain Assemblies. Mechanics of Cohessive Frictional Matter, 4, pp. 461-486. [ Links ]
Huang , W. (2000). Hypoplastic Modelling of Shear Localisation in Granular Materials. Doctoral Thesis, Graz University of Technology. [ Links ]
Maier, T. (2004). Comparison of Nonlocal and Polar Modeling of Softening in Hypoplasticity, International Journal of Numerical and Analytical Methods in Geomechanics, 28, pp. 251-268. [ Links ]
Masson, S.; Martínez, J. (2001). Micromechanical Analysis of the Shear Behavior of a Granular Material. Journal of Engineering Mechanics. 127 (10), pp. 1007-1016. [ Links ]
Orlando, A.; Hanes, D.; Shen, H. (2009). Scaling Effects in Direct Shear Test. Powders and Grains 2009. Proccedings of the 6th International Conference on Micromechanics of Granular Media. AIP Conference Proceedings Col 1145 Issue 1. [ Links ]
Palmeira, E.; Milligan, G. (1989). Scale Effects in Direct Shear Test on Sand. Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering. 1 (1), pp. 739-742. [ Links ]
Ramos, A.; Lizcano, A. (2010). Aspectos que afectan las bandas de corte en simulaciones numéricas con elementos finitos de ensayos de deformación plana con un modelo constitutivo hipoplástico. Revista Técnica de la Facultad de Ingeniería Universidad del Zulia, 33 (2), pp. 153-163. [ Links ]
Romano, A.; Lancellota, R.; Marasco, A. (2004). Continuum Mechanics Using Mathematica. Fundamentals Applications and Scientific Computing. Birkhauser. [ Links ]
Skempton, A.; Bishop, A. (1950). The Measurements of the Shear Strength of Soils. Geotechnique, 2, pp. 188-192. [ Links ]
Tejchman, J.; Bauer, E. Numerical Simulation of Shear Band Formation with a Polar Hypoplastic Constitutive Model. Computers and Geotechnics, 19 (3), pp. 221-244. [ Links ]
Tejchman, J. (1997). Modelling of Shear Localization and Autogeneous Dynamic Effects in Granular Bodies. Publication Series of the Institute for Rock and Soil Mechanics. University Karlsruhe, 140. [ Links ]
Tejchman, J. (2005). Finite Element Modeling of Shear localization in granular bodies in hypoplasticity with Enhancements. Gdansk University of Technology Publisher. Gdansk. [ Links ]
Wu, P.; Matsushima, K.; Tatsuoka F. (2008). Effects of Specimen Size and Some other Factors on the Strength and Deformation of Granular Soil in Direct Shear Tests. Geotechnical Testing Journal, 31 (1), pp. 1-20. [ Links ]
Xuebin, W.; Jupeng, T.; Zhihui, Z.; Yashan, P. (2004). Analysis of Size Effect, Shear Deformation and Dilatation in Direct Shear Test Based on Gradient-Dependent Plasticity. Chinese Journal of rock mechanics and Engineering. 23 (7), pp. 1095-1099. [ Links ]
Zhang, L.; Thornton, C. (2007). A Numerical Examination of the Direct Shear Test. Geotechnique, 57 (4), pp. 343-354. [ Links ]
Zhou, Q.; Helenbrook, B.; Shen, H. (2009). A Computational Study of the Micromechanics Under Pre and Post-Failure in a 2-D Direct Shear Test, Chinese Science Bulletin. Disponible en Doi:10.1007/s11434-009-0516-5. [ Links ]