ANÁLISIS NUMÉRICO DEL PROCESO DE INFILTRACIÓN DE AGUA Y LOCALIZACIÓN DE DEFORMACIÓN EN SUELOS PARCIALMENTE SATURADOS

NUMERICAL ANALYSIS OF THE WATER INFILTRATION PROCESS AND STRAIN LOCALIZATION IN PARTIALLY SATURATED SOILS

ANÁLISE NUMÉRICA DO PROCESSO DE INFILTRAÇÃO DA AGUA E LOCALIZAÇÃO DE DEFORMAÇÃO EM SOLOS PARCIALMENTE SATURADOS

Willideman Tobón Sánchez¹, Edwin Fabián García Aristizábal², Carlos Alberto Vega Posada³

1 Ingeniería Civil - Udea, Maestría en Ingeniería Civil - Politecnico di Torino. Politecnico di Torino.
2 Ingeniería Civil - Unal, Máster en Ingeniería - U de Tokyo, Doctor en Ingeniería - U de Kyoto. Universidad de Antioquia. Calle 67 Número 53 - 108, oficina 20-439, Medellín, Colombia / Tel: (574) 219 85 73. Correo electrónico: edwin.garcia@udea.edu.co.
3 Ingeniería Civil - Unal, MSc - Ohio University, Ph.D - Northwestern University. Universidad de Antioquia.

Artículo recibido: 28-IV-2015 / Aprobado: 06-IV-2016
Disponible online: 30 de octubre de 2016
Discusión abierta hasta octubre de 2017

RESUMEN

En este trabajo se presentan simulaciones del proceso de infiltración de agua en suelos parcialmente saturados en una y en dos dimensiones, haciendo uso de un método acoplado infiltración-deformación. El estudio de la infiltración unidimensional se realizó en dos partes: primero, considerando un suelo homogéneo y, posteriormente, un suelo estratificado compuesto de dos horizontes diferentes. Para ambos casos se modelaron columnas unidimensionales de un metro de espesor, con las que se realizó un estudio paramétrico tomando diferentes valores de Intensidad de lluvia. Del análisis se encontró que el fenómeno de infiltración unidimensional tiene una alta dependencia de la relación intensidad de lluvia (I)/Permeabilidad del suelo (k_s^W) y en el caso de los suelos estratificados se evidenció un control de la infiltración por parte del suelo de menor permeabilidad. Finalmente, se analizó el caso de infiltración bidimensional mediante la modelación de un talud sometido a lluvia de alta intensidad donde se pudo localizar la superficie de falla en el talud. Los resultados de este análisis muestran el potencial de esta metodología para el estudio de estructuras de suelo sometidas a procesos de infiltración.

PALABRAS CLAVE: suelos parcialmente saturados; infiltración; intensidad de lluvia; localización de deformación; análisis numérico.

ABSTRACT

This paper presents one- and two-dimensional simulations of the water infiltration process on unsaturated soils by using a coupled infiltration-deformation model. Two examples are presented for the one-dimensional infiltration analysis. The first example simulates the infiltration process on a homogenous soil, and the second on a stratified soil composed of two different layers. For both cases, a one-meter column of soil was used to conduct a parametric study by assuming different values of rainfall intensity. It was found from this analysis that the one-dimensional infiltration process on the homogenous soil is highly dependent on the rainfall intensity (I) / permeability (k_s^W) ratio, and for the stratified soil, the infiltration process was controlled by the soil with less permeability. Finally, one example is presented to study the bi-dimensional infiltration process on a slope subjected to a high-intensity rainfall, where the localization of the failure surface is presented. The results of this analysis show the advantages of this methodology to study soil structures subjected to infiltration processes.

KEY WORDS: Unsaturated soils; Infiltration; Rainfall intensity; Strain localization; Numerical analysis.

RESUMO

Neste trabalho apresentam-se simulações do processo de infiltração da agua em solos não saturados em uma e duas dimensões, mediante a utilização de um código acoplado infiltração-deformação. O estudo da infiltração unidimensional realizou-se em duas partes: primeira, considerando um solo homogêneo e, posteriormente, um solo estratificado com uma configuração de duas camadas diferentes. Em ambos os casos as simulações consideraram colunas unidimensionais de um metro de comprimento com as quais foram feitas análises paramétricas para diferentes valores de intensidade da precipitação. As análises mostraram que o processo de infiltração unidimensional é altamente dependente da relação Intensidade da precipitação (I) / Permeabilidade do solo (k_s^W) e, no caso do solo estratificado evidenciou-se que a infiltração está governada pela camada de menor permeabilidade. Finalmente, analisou-se o caso da infiltração bidimensional mediante a modelagem de um talude submetido a uma precipitação de alta intensidade sendo possível identificar a aparição da superfície de ruptura no talude. Os resultados desta análise mostraram o potencial desta metodologia para o estudo de estruturas geotécnicas submetidas a processos de infiltração.

PALAVRAS-CHAVE: Solos parcialmente saturados; Infiltração; Intensidade de precipitação; Localização da superfície de ruptura; Análises numéricas.

1. INTRODUCCIÓN

Actualmente, los análisis numéricos acoplados para suelos parcialmente saturados están siendo cada vez más utilizados para estudiar problemas relacionados con el efecto de la infiltración de agua en la estabilidad de taludes y terraplenes. Las fallas en estas estructuras ocurren frecuentemente debido a diferentes condiciones de lluvia que involucran periodos cortos y largos de duración. Cuando el agua se infiltra en los suelos parcialmente saturados incrementa su humedad. Consecuentemente, genera cambios en las presiones de poros (reducción de la succión) reduciendo la resistencia al corte del material. Por esta razón, el estudio de la infiltración de agua en suelos parcialmente saturados y su efecto en la deformación es un tema de amplio interés que todavía necesita ser investigado en el campo de la geotecnia.

Varios investigadores han estudiado de manera experimental el proceso de infiltración de agua en suelos parcialmente saturados (Liakopoulos, 1964; Yang et al., 2004; Bathurst et al., 2007). De igual manera, Sryvastava & Yeh (1991) plantearon soluciones analíticas para describir el proceso de infiltración en una dimensión en suelos homogéneos y estratificados, cuyos resultados fueron usados por Zhang & Ng (2004) para analizar el efecto de los parámetros hidráulicos y condiciones de lluvia en el proceso de infiltración. Los primeros en obtener una solución analítica para el proceso de infiltracióndeformación unidimensional fueron Wu & Zhang (2009), quienes usaron un modelo constitutivo planteado por Fredlund (1993), y cuyos resultados mostraron que las variables más importantes en la distribución de succión en una columna de suelo y su deformación son: los cambios de volumen debidos a cambios en la succión, la relación entre la intensidad de lluvia y la permeabilidad saturada del suelo (I/k_s^W). Recientemente, Wu et al. (2015) presentaron una solución analítica acoplada para una frontera de flujo variable mostrando que el acoplamiento de la infiltración y la deformación tienen un efecto significativo en la distribución de presiones para un flujo transitorio en suelos no saturados. Esto demuestra que es necesario realizar un análisis acoplado de infiltración-deformación para analizar de manera más certera el problema de infiltración en suelos parcialmente saturados.

Actualmente, las soluciones numéricas se han convertido en una herramienta de análisis potencial debido a la facilidad de implementar con ellas diferentes tipos de fronteras y condiciones iniciales, variedad de suelos estratificados, intensidades de lluvias variables y geometrías complejas, lo cual permite una mejor aproximación a los problemas que se presentan en ingeniería geotécnica. De esta manera, varios autores han desarrollado soluciones numéricas para el estudio de infiltración de agua en medios porosos; Cai & Ugai (2004) investigaron los efectos de las características hidráulicas en el flujo transitorio de agua a través de taludes saturados y parcialmente saturados y la implicación que tienen en su resistencia. Pinder & Gray (2008) estudiaron el comportamiento de infiltración y drenaje de aire y agua en suelos homogéneos y heterogéneos. Griffiths & Lu (2005) usaron la definición de Bishop para el esfuerzo efectivo en suelos parcialmente saturados junto con la teoría de succión unidimensional para analizar la estabilidad de un talud debido a la infiltración de agua. Ehlers et al. (2004) usaron un método acoplado de infiltración-deformación que incluía los términos de presión de poros efectiva y esfuerzo efectivo para calcular deformaciones en suelos parcialmente saturados debidas a flujo de agua. Igualmente, Cho & Lee (2001) utilizaron este tipo de modelos para analizar estabilidad en taludes, y Alonso et al. (2003) para calcular las deformaciones y la variación del factor de seguridad de un talud inestable en un perfil de arcilla sobreconsolidada. Oka et al. (2009), Kato et al. (2009) y Kimoto et al. (2013) investigaron las características de un proceso acoplado de infiltración-deformación en diques y terraplenes parcialmente saturados. Wu & Selvadurai (2016) investigaron el efecto de condiciones variables de la frontera de infiltración en horizontes de suelo homogéneo, encontrando que el acoplamiento tiene una influencia significativa en la posición de los niveles de agua acumulada.

La ventaja de las metodologías acopladas infiltración-deformación, es que permiten tener en cuenta los cambios en las condiciones de esfuerzo efectivo y deformación del material debidos a la variación del grado de saturación producido por el proceso de infiltración de agua. Esto posibilita el estudio de la distribución de la deformación y la localización de la superficie de falla más probable, lo cual no es posible cuando se usan metodologías clásicas de análisis de estabilidad de taludes.

En este trabajo se presenta un modelo acoplado infiltración-deformación, y posteriormente, utilizando esta metodología, se examinan los siguientes casos de estudio y de interés en ingeniería: (1) proceso de infiltración unidimensional en un suelo homogéneo, (2) proceso de infiltración unidimensional en suelos estratificados y (3) distribución o localización de la superficie de falla en un talud homogéneo. Los análisis presentados pretenden examinar el fenómeno de infiltración y deformación de suelos, así como mostrar las ventajas que proporcionan los métodos acoplados para investigar problemas de infiltración facilitando la observación en el tiempo de las variables más importantes que allí intervienen. De esta manera, se presentan resultados de un estudio de la variación de la saturación, la succión y la deformación cuando los materiales se someten a diferentes escenarios de infiltración.

Modelo acoplado infiltración-deformación

Oka et al. (2006) formularon un método acoplado de infiltración-deformación basado en elementos finitos y utilizaron un modelo viscoplástico para la descripción del comportamiento de suelos parcialmente saturados (Kimoto & Oka, 2005). Esta metodología es utilizada para los casos de análisis presentados más adelante. La metodología propuesta está basada en los conceptos fundamentales de la Teoría de Medios Porosos (e.g., Biot, 1962; Atkin & Craine, 1976; Boer, 1998; Ehlers, 2003). Se asume que el suelo está compuesto por tres fases: sólida, líquida y gaseosa, las cuales están distribuidas de manera continua a través del espacio. Durante el análisis se tienen como variables independientes la presión del agua, la presión del aire y la deformación. A continuación se describen los componentes de la metodología y las ecuaciones empleadas:

Variables de esfuerzos

El comportamiento del material está descrito dentro del marco de la mecánica del medio continuo a través del uso de la teoría de Medios Porosos. Terzaghi (1943) definió el concepto de esfuerzo efectivo para materiales saturados. Sin embargo, los procesos de infiltración se dan en su mayoría en suelos parcialmente saturados, por lo tanto, el concepto de esfuerzo efectivo debe ser redefinido con el objeto de considerar una fase gaseosa incluida en los poros del material.

Con el objeto de definir los esfuerzos que se presentan en el suelo parcialmente saturado, se adopta un esfuerzo efectivo para el esqueleto granular σ'_ij (Oka et al. 2010), que es análogo al esfuerzo efectivo de suelos saturados. El tensor total de esfuerzos, σ_ij, se obtiene de sumar los esfuerzos parciales así:

donde P^W y P^G son las presiones de agua y aire, respectivamente; n es la porosidad; n^γ es la fracción volumétrica de la fase γ (γ = S: Sólido, W: Agua, G: Aire); δ_ij es la función delta de kronecker y PF es el promedio de las presiones de poros calculados de acuerdo con la saturación s de la siguiente manera:

De las Ecuaciones 1 a 5 se deriva la ecuación de esfuerzo efectivo para suelo parcialmente saturado,

Conservación de masa

La conservación de la masa está dada por la siguiente ecuación:

en donde ρ^γ es la densidad del material y v_i^γ es la velocidad de la fase γ. Suponiendo que las derivadas espaciales de la fracción volumétrica n_γ son despreciables, y que las partículas sólidas y el agua son incompresibles, las leyes de conservación para las fases de agua y de aire se pueden expresar en función de s y n, así:

donde D_ii es la deformación volumétrica y V_i^γ es la velocidad aparente de la fase γ.

Ecuación de equilibrio

La variación de la ecuación de equilibrio se puede expresar de la siguiente manera:

en donde _ij es el tensor de esfuerzo nominal.

Curva de retención de agua

La relación entre saturación y succión se da por medio de la ecuación propuesta por Van Genuchten (1980), presentada a continuación:

en la cual P^C es la succión; α, n', y m son parámetros del material, donde m = 1-1/n'; s_max y s_min son los límites máximo y mínimo de la saturación, respectivamente. El efecto del grado de saturación sobre las permeabilidades de los fluidos se adopta de la siguiente manera:

donde a y b son parámetros del material, k_s^W es el coeficiente de permeabilidad para el agua en condición de suelo saturado y k_s^G es el coeficiente de permeabilidad para el aire en condición de suelo seco.

Modelo constitutivo para suelo parcialmente saturado

Kimoto & Oka (2005) formularon un modelo constitutivo viscoplástico para la descripción del comportamiento de suelos parcialmente saturados. En este modelo se asume que existe una superficie de sobreconsolidación (fb) que delimita una región normalmente consolidada (NC) y otra región sobreconsolidada (OC), la cual se describe con las siguientes ecuaciones:

donde η*_ij = S_ij/σ'_m, S_ij es el tensor del esfuerzo desviador, σ'_m es el esfuerzo efectivo medio, M_m* es el valor de cuando el incremento de la deformación volumétrica cambia de compresión a dilatación, el cual es igual a M_f* en el estado crítico. σ'_mb es el parámetro de endurecimiento del material el cual controla el tamaño de la superficie de frontera. El efecto de la succión se incorpora en el modelo como:

donde es la deformación viscoplástica volumétrica, λ y κ son los coeficientes de compresión y expansión, respectivamente; y e₀ es la relación de vacíos inicial. P_i^C es el valor de la succión inicial, P^C es el valor de succión actual, S_I es el parámetro que denota el cambio de resistencia del material desde su condición de succión inicial hasta que alcanza la saturación. S_d es el parámetro que controla el cambio de incremento o disminución de la resistencia con el cambio de succión. σ'_ma es el parámetro de ablandamiento usado para describir la degradación del material debido a cambios estructurales.

La función de fluencia del material está dada por:

De esta manera, aquí se introduce el efecto de la succión a través de valor de σ'_my^(s), así:

El tensor de deformación volumétrica está dado por las siguientes ecuaciones:

en donde f_p es la superficie de potencial viscoplástico, Φ₁ denota una función del efecto de velocidad de carga, A y B son parámetros del material, los cuales tienen relación con la componente desviadora C₁ y la componente volumétrica C₂ de los parámetros viscoplásticos.

2. SIMULACIONES Y RESULTADOS NUMÉRICOS

Caso 1: Infiltración unidimensional en una columna de suelo homogéneo

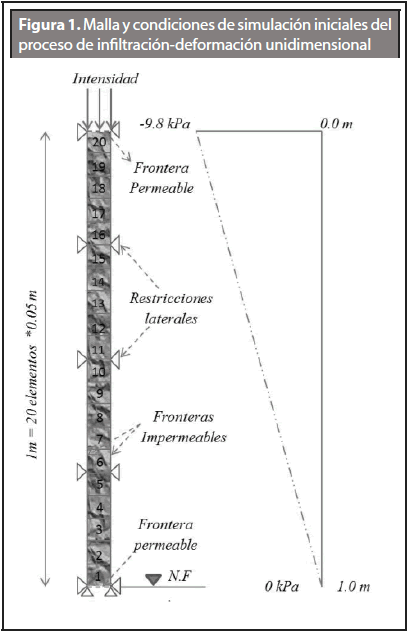
La simulación del proceso de infiltración se realizó sobre una columna de 1 metro de espesor compuesta de un estrato homogéneo de arena, representada mediante una malla compuesta de 20 elementos cuadrados de 5 cm de lado, los cuales se encuentran restringidos horizontalmente. La base de la columna está restringida en ambas direcciones, permitiendo solo la deformación vertical de los elementos. La columna posee fronteras laterales impermeables, el aire es evacuado por la frontera superior, al mismo tiempo que esta recibe agua de lluvia que penetra a la columna de suelo variando sus condiciones de humedad por la infiltración de agua. La base de la columna es una frontera drenada, la cual permite el paso de agua desde el interior de la columna hacia estratos inferiores. Se supone un nivel freático inicial ubicado en el límite inferior de la columna y una distribución de succión lineal a través del suelo parcialmente saturado. La malla de elementos finitos y las condiciones iniciales para la simulación se representan en la Figura 1.

Para la simulación se generó una lluvia de intensidad constante menor o igual a la permeabilidad saturada del suelo, lo que garantiza que no se presente acumulación de agua en la superficie y todo el volumen de agua es introducido en el suelo. La lluvia se aplicó en la superficie de la columna por un periodo de 30 h, el cual permite mostrar una tendencia típica del proceso de infiltración para la permeabilidad del suelo. Se realizó un análisis paramétrico en el estrato arenoso, manteniendo constante la permeabilidad para el agua en estado saturado (k_s^W = 1*10^-6 m/s) y cambiando la intensidad de la lluvia (I), la cual toma valores de I = 0.2k_s^W, 0.4k_s^W, 0.6k_s^W, 0.8k_s^W y k_s^W.

Los parámetros que definen la curva característica de retención de agua, para el suelo parcialmente saturado se muestran en la Tabla 1. α, n' y s_max corresponden a las variables de la ecuación de Van Genuchten (1980) utilizadas para relacionar la saturación y la succión del suelo, y a es un parámetro propio del suelo que permite definir la variación de la permeabilidad para el agua con la saturación del suelo. Los parámetros presentados en la Tabla 1, son parámetros típicos de suelos arenosos (Lu y Likos, 2004).

Con el objeto de analizar la respuesta del suelo durante el proceso de infiltración se grafican los resultados comparativos de los perfiles de succión y saturación para una intensidad de lluvia I = 0,2k_s^W.

En la Figura 2(a) se observan los perfiles de succión para los tiempos t = 0, 1, 5, 10, 20 y 30 h, los cuales muestran poca variación en la succión del suelo, esto debido a que la intensidad de lluvia no es alta con respecto a la permeabilidad del suelo (I = 0,2k_s^W), representando una capacidad de infiltración que supera bastante a la intensidad de lluvia. La disminución de la succión es mayor en la superficie y muestra su avance en el tiempo, indicando el incremento del contenido de agua en el suelo. Igualmente, los resultados anteriores se verifican en la Figura 2(b) donde se presentan los perfiles de saturación para la misma intensidad de lluvia; se observa que el grado de saturación en la superficie aumenta desde la primera hora de infiltración haciéndose mayor a medida que avanza el tiempo, y disminuye en profundidad.

Figura 2

Para analizar la respuesta a la intensidad de la lluvia, se presentan en la Figura 3(a) los perfiles de succión correspondientes a una lluvia de 30 h, para diferentes intensidades de lluvia (i.e. I = 0,2k_s^W, 0,4k_s^W, 0,6k_s^W, 0,8k_s^W y k_s^W). Los resultados muestran perfiles de succión con valores máximos en la superficie de la columna y que disminuyen a medida que se incrementa la profundidad, hasta llegar a valores de cero en la base de la misma, donde se encuentra localizado el nivel freático. A medida que la intensidad de la lluvia aumenta, la succión se hace más pequeña debido al mayor contenido de agua en el suelo. Igualmente, la Figura 3(b) muestra la variación de la saturación con la intensidad de la lluvia, indicando que a medida que la intensidad se incrementa la saturación en el suelo aumenta.

Figura 3

Finalmente, cuando la intensidad de la lluvia se acerca a la permeabilidad saturada del suelo, la succión se hace cero y la saturación se hace máxima a todo lo largo de la columna para el tiempo de simulación. Esto indica que entre mayor sea la relación I/k_s^W más rápido se dará la disminución de succión y el incremento de la saturación en la columna de suelo. Estos resultados concuerdan con los resultados obtenidos experimentalmente por Yang et al. (2006).

Caso 2: Infiltración unidimensional en una columna de suelo estratificado

En este caso se analizó el flujo unidimensional en un suelo estratificado, donde las propiedades hidráulicas del suelo cambian para cada material. Se utilizó para la simulación una columna de 1 m de espesor compuesta por un estrato de suelo arenoso y un estrato de suelo arcilloso, la posición de los estratos varía con el objeto de estudiar las diferencias en el proceso de infiltración (Ver Figura 4). Los parámetros que describen la curva característica de retención de agua son, para la arena α = 0,1 kPa^-1, n' = 4 y k_s^W = 10^-6 m/s; para la arcilla α = 0,071 kPa^-1, n' = 1,3 y k_s^W = 10^-8 m/s (Lu & Likos, 2004).

Figura 4

Arcilla sobre arena

La Figura 5(a) exhibe los perfiles de succión obtenidos para una columna de suelo conformada por un horizonte de arcilla de 0,5 m de espesor, el cual se encuentra sobre un horizonte de arena de 0,5 m de espesor. La columna de suelo fue sometida a un proceso de inundación durante 200 h con el objetivo de garantizar el ingreso de agua a través de toda la columna. En esta figura se observan valores de succión que van disminuyendo con el avance del tiempo pero solo en la superficie del horizonte superior (arcilla). Adicionalmente, no se observa una variación en los perfiles de succión en el horizonte arenoso, esto debido a que el agua que llega a este horizonte se evacúa rápidamente debido a la mayor permeabilidad del suelo sin afectar considerablemente sus condiciones de saturación. Esto se ratifica observando la Figura 5(b) en la que se presentan perfiles de saturación constantes para el estrato arenoso, pero que aumentan para la arcilla a medida que avanza el tiempo de infiltración.

Figura 5

En este caso, se evidencia el comportamiento de un horizonte de suelo que actúa como barrera y otro horizonte que actúa como un filtro, el estrato superior (suelo fino) es un estrato relativamente impermeable que retiene el agua y dificulta su paso hacia horizontes inferiores, y el estrato inferior (suelo granular) funciona como un medio filtrante, facilitando la evacuación del agua infiltrada e impidiendo su acumulación.

Arena sobre Arcilla

La Figura 6(a) presenta los perfiles de succión obtenidos para el caso en el cual el horizonte de arcilla subyace un horizonte de arena. La columna de suelo se sometió a un proceso de inundación durante 10 h, el cual es suficiente para garantizar el ingreso de agua a través de toda la columna.

Figura 6

En la figura se observan las caídas de succión en tiempos menores si se compara con el caso de los horizontes arcilla-arena (200 h); después de 5 h el estrato arenoso está saturado (Figura 6(b)) y la succión constante en un valor de cero; sin embargo, el estrato inferior (arcilla) aún posee succión; esto debido a que el estrato arcilloso no está saturado, condicionado por su incapacidad de permitir el paso de toda el agua que le llega desde el estrato superior, ya que su permeabilidad es menor.

Estos tipos de perfiles traen como consecuencia niveles freáticos "colgados", en donde el agua que se infiltra por la superficie se encuentra con estratos impermeables que impiden su paso y causan una acumulación del agua, saturando los estratos superiores; por lo que muchas veces es confundido con el nivel freático real del suelo. Este tipo de acumulaciones trae como resultado fallas superficiales de taludes y terraplenes (Abramson et al., 2002).

Caso 3: Infiltración bidimensional en talud homogéneo

En este caso se utilizó el modelo acoplado infiltración- deformación presentado previamente para analizar la infiltración de la lluvia en un talud homogéneo. En la Figura 7 se presenta la zonificación espacial del talud; la posición del nivel freático se encuentra en la parte baja del talud y se supone una distribución lineal de la succión inicial hasta una altura de 1 m desde el nivel freático, a partir de la cual es constante. La presión del aire se asume igual a la atmosférica. El aire puede ser drenado por cualquiera de las fronteras que conforman el talud. Se genera una lluvia de intensidad conocida como condición de frontera en la superficie del talud la cual permite entrada de agua de acuerdo con la intensidad de la lluvia y el nivel de succión del material. La base del talud es impermeable y está sujeta a restricción de movimiento lateral y vertical. Las fronteras laterales bajo el nivel freático son permeables y están restringidas horizontalmente.

Figura 7

Los parámetros del suelo utilizados en la simulación se presentan en la Tabla 2. Estos parámetros representan un suelo limoso. Se generó una lluvia de Intensidad I = 30 mm/h (8,33*10^-6 m/s) con una duración de 48 h. Durante este tiempo, se incrementó el nivel freático en la frontera derecha del talud con el objeto de simular un flujo lateral. De este proceso de infiltración se analizó el comportamiento del talud mediante la evolución de la saturación y deformación viscoplástica acumulada. Se consideró un suelo con una permeabilidad saturada de 3*10^-5 m/s. Los parámetros presentados en la Tabla 2, fueron utilizados en simulaciones de infiltración-deformación en diques por Kimoto et al. (2013).

Tabla 2

Los parámetros del suelo presentados en la Tabla 2 se obtienen de ensayos experimentales de compresión no drenada, consolidación y permeabilidad, de la siguiente manera:

• El parámetro viscoplástico m' se obtiene por medio de ensayos de compresión triaxial no drenada a diferentes velocidades de deformación.
• Los parámetros viscoplásticos C₁ y C₂ se obtienen con base en la Ecuación 19.
• La relación de esfuerzos en estado crítico M*_m se determina por la relación de esfuerzos en estado residual.
• El índice de compresión λ y de expansión κ se obtienen por medio de ensayos de consolidación.
• El módulo de cortante elástico G₀ se obtiene de la pendiente inicial del ensayo de compresión triaxial (G₀ = Δq/(3Δε₁₁)).
• La relación de vacíos e₀ se determina de los ensayos de propiedades físicas.
• El parámetro estructural β se determina por medio de ajuste en la zona de ablandamiento de la curva q-ε.
• Los parámetros S_I y S_d se obtienen por ajuste de la curva de incremento de la resistencia debido a la succión.
• El parámetro b se obtiene por ajuste de la curva de permeabilidad para el aire.

La Figura 8 muestra el avance del frente de saturación para el talud analizado desde antes de que comience la lluvia (t = 0), en el que solo el suelo bajo el nivel freático está saturado. Sobre el nivel freático el suelo se encuentra parcialmente saturado con grados de saturación mayores al 50%. De esta figura, se puede observar que, a medida que el tiempo de lluvia avanza, los valores de saturación se incrementan, aumentando inicialmente en las fronteras superiores del talud, debido a la lluvia que se recibe directamente por ellas, y en la frontera derecha debido al flujo de infiltración horizontal. A las 27 h de lluvia se presenta un área al interior del talud que aún permanece con los valores iniciales de saturación, debido a que ni el frente húmedo, ni el flujo lateral han concurrido. Dado que un mayor grado de saturación representa menores valores de permeabilidad para el aire, el avance de agua impide la salida rápida del mismo, el cual queda atrapado en el suelo, restringiendo el avance del frente húmedo. Para el tiempo final de la simulación se observa un alto grado de saturación en el material.

Figura 8

Para el análisis de la deformación, se considera que la falla en un suelo se alcanza en la práctica cuando su deformación unitaria acumulada no recuperable supera un valor del 5%. En la Figura 9 se toman intervalos de deformación con este valor como máximo a partir de las 35 h de infiltración. Las primeras apariciones de deformación viscoplástica que superan el 1,5% se dan a las 40 h, y ocurren en la base del talud. A partir de estas pequeñas deformaciones se empieza a formar una superficie de falla que asciende desde la pata del talud hasta su cresta. A las 47 h de simulación es posible observar que la superficie de falla presenta en casi toda su longitud deformaciones mayores a 5%.

Figura 9

Analizando el avance de la deformación viscoplástica en el tiempo, se aprecia una falla de tipo rotacional en el talud. Esta superficie localizada se presenta por el incremento del peso de la masa de suelo y la reducción de la resistencia al corte por la infiltración de agua lluvia. La superficie de falla encontrada por medio de la simulación resulta naturalmente del proceso de infiltración, lo que convierte esta metodología de análisis en una herramienta potencial para obtener análisis de estabilidad más certeros de taludes y terraplenes.

La metodología acoplada infiltración-deformación empleada para los análisis no presenta limitaciones para estudiar ningún tipo de obra geotécnica. Debido a su flexibilidad, permite analizar la interacción de diferentes tipos de materiales (e.g. suelos, concretos, drenajes, geosintéticos, etc.), con diferentes tipos de fronteras (e.g, infiltración, evaporación, sobrecarga, remoción de carga, deformación, etc.). Sin embargo, la complejidad de esta metodología implica la obtención de parámetros geotécnicos e hidráulicos adicionales para determinar las relaciones esfuerzo-deformación de los materiales a diferentes grados de saturación.

Estas metodologías presentan como ventaja un resultado más certero del análisis del comportamiento de la estructura ante un evento transitorio.

3. CONCLUSIONES

Los problemas relacionados con suelos parcialmente saturados son comunes en el campo de la ingeniería; su estudio se ha venido implementando mediante modelaciones numéricas que permiten introducir diferentes condiciones de frontera para el estudio de casos reales e hipotéticos relacionados con la infiltración de agua. El modelo acoplado infiltración- deformación presentado permite el análisis de los procesos de avance de flujos de agua en suelos homogéneos y estratificados por medio del seguimiento de los cambios en la succión, la saturación y las deformaciones generadas por el cambio en los esfuerzos efectivos.

Del análisis del proceso de infiltración unidimensional en suelo homogéneo, se observa el efecto de la intensidad de la lluvia en el suelo, mostrando que entre mayor sea la relación I/k_s^W más rápido se dará la disminución de succión y el incremento de la saturación en la columna de suelo.

Para los casos simulados en suelos estratificados, se encuentra que cuando el horizonte de arcilla está localizado sobre el horizonte de arena, se presenta dificultad en la entrada de agua; pero una vez esta llega al horizonte arenoso fluye rápidamente debido a su mayor permeabilidad, haciendo el papel de capa filtrante. Cuando la arena es el horizonte superior el agua se infiltra rápidamente y la arcilla controla su salida, causando niveles freáticos colgados y la saturación completa del horizonte superior. En otras palabras, la arcilla controla el proceso de infiltración bien sea reduciendo la infiltración del agua cuando se encuentra en la superficie o reteniéndola cuando se encuentra como un horizonte subyacente.

Finalmente, para el análisis bidimensional del proceso de infiltración en un talud homogéneo, se observa que cuando se aplica la lluvia, los cambios de saturación y succión se inician cerca de la superficie y avanzan en profundidad a medida que se incrementa la duración de la lluvia. El proceso de infiltración trae consigo cambios en las condiciones de esfuerzo efectivo del material, lo que posibilita (por medio de las relaciones esfuerzo-deformación incluidas en el modelo) el estudio de la distribución de la deformación y la localización de la superficie de falla más probable, lo cual no es posible cuando se usan metodologías clásicas de análisis de estabilidad de taludes.

REFERENCIAS

Abramson, L.W.; Lee, T.S.; Sharma, S.S.; Boyce, G.M. (2002). Slope Stability and Stabilization Methods. New York, U.S.A.: Wiley. 712 p.         [ Links ]

Alonso, E.E.; Gens, A.; Delahaye, C.H. (2003). Influence of Rainfall on the Deformation and Stability of a Slope in Overconsolidated Clays: A Case Study. Hydrogeology Journal, 11(1), febrero pp. 174-192.         [ Links ]

Atkin, R.J.; Craine, R.E. (1976). Continuum Theories of Mixtures: Basic Theory and Historical Developments. The Quarterly Journal of Mechanics and Applied Mathematics, 29(2), abril, pp. 209-244.         [ Links ]

Bathurst, R.J.; Ho, A.F.; Siemens, G. (2007). A Column Apparatus for Investigation of 1-D Unsaturated-Saturated Response of Sand-Geotextile Systems. Geotechnical Testing Journal, 30(6), octubre, pp. 1-9.         [ Links ]

Biot, M.A. (1962). Mechanics of Deformation and Acoustic Propagation in Porous Media. Journal of Applied Physics, 3(4), abril, pp. 1482-1498.         [ Links ]

Boer, R.D. (1998). Theory of Porous Media - Past and Present. Journal of Applied Mathematics and Mechanics. 78(7), junio, 441-466.         [ Links ]

Cai, F.; Ugai, K. (2004). Numerical Analysis of Rainfall Effects on Slope Stability. International Journal of Geomechanics, 4(2), pp. 69-78.         [ Links ]

Cho, S.E.; Lee, S.R. (2001). Instability of Unsaturated Soil Slopes Due to Infiltration. Computers and Geotechnics, 28(3), abril, pp. 185-208.         [ Links ]

Ehlers, W. (2003). Continuum and Numerical Simulation of Porous Materials in Science and Technology. In Capriz, G.; Ghionna, V.N. and Giovine, P. eds. Modeling and Mechanics of Granular and Porous Materials. Birkhäuser. Ch. 9.         [ Links ]

Ehlers, W.; Graf, T.; Amman, M. (2004). Deformation and Localization Analysis of Partially Saturated Soil. Computer Methods in Applied Mechanics and Engineering, 193(27-29), julio, pp. 2885-2910.         [ Links ]

Fredlund, D.G.; Rahardjo, H. (1993) Soil Mechanics for Unsaturated Soils. New York, U.S.A.: Wiley. 544 p.         [ Links ]

Griffiths, D.V.; Lu, N. (2005). Unsaturated Slope Stability Analysis With Steady Infiltration Or Evaporation Using Elasto-Plastic Finite Elements. International Journal for Numerical and Analytical Methods in Geomechanics, 29, pp. 249-267.         [ Links ]

Kato, R.; Sunami, S.; Oka, F.; Kimoto, S.; Kodaka, T. (2009). A Multi-Phase Elasto-Viscoplastic Analysis of a Unsaturated River Embankment Associated with Seepage Flow. In Kyoto, Japan, Oka, F., Murakami, A., and Kimoto, S. eds. Proceedings of the International Symposium on Prediction and Simulation Methods for Geohazard Mitigation. London, U.K.: Taylor and Francis Group. Pp. 401-407.         [ Links ]

Kimoto, S.; Oka, F. (2005). An Elasto-Viscoplastic Model for Clay Considering Destructuralization and Consolidation Analysis of Unstable Behavior. Soils and Foundations, 45(2), marzo, pp. 29-42.         [ Links ]

Kimoto, S.; Oka, F.; Garcia. E. (2013). Numerical Simulation of the Rainfall Infiltration on Unsaturated Soil Slope Considering a Seepage Flow. Geotechnical Engineering Journal of the SEAGS & AGSSEA, 44(3), agosto, pp. 1-13.         [ Links ]

Liakopoulos, A. (1964). Transient Flow Through Unsaturated Porous Media. Ph.D. University of California at Berkeley.         [ Links ]

Lu, N.; Likos, W. (2004) Unsaturated Soil Mechanics. New Yersey, U.S.A.: Wiley. 556 p.         [ Links ]

Oka, F.; Kimoto, S.; Takada, N.; Higo, Y. (2009). A Multi-Phase Elasto-Viscoplastic Analysis Of A Unsaturated River Embankment Associated With Seepage Flow. In Mitigation, Kyoto, Japan, Oka, F., Murakami, A., and Kimoto, S. eds. Proceedings of the International Symposium on Prediction and Simulation Methods for Geohazard Mitigation. London, U.K.: Taylor and Francis Group. Pp. 127-132.         [ Links ]

Oka, F.; Kodaka, T.; Kimoto, S.; Kim, Y.-S.; Yamasaki, N. (2006). An Elastoviscoplastic Model and Multiphase Coupled FE Analysis for Unsaturated Soil. In Miller, G.A., Zapata, C.E.; Houston, S.L. and Fredlund, D.G. eds. Proceedings of the fourth international conference on unsaturated soils. Arizona, U.S.A.: Geotechnical Special Publication - American Sociecty of Civil Engineers. Pp. 124-131.         [ Links ]

Oka, F.; Kodaka, T.; Suzuki, H.; Kim, Y.S.; Nishimatsu, N.; Kimoto, S. (2010). Experimental Study On The Behavior Of Unsaturated Compacted Silt Under Triaxial Compression. Soils and Foundations, 50(1), pp. 27-44.         [ Links ]

Pinder, G.F.; Gray, W.G. (2008) Essentials of Multiphase Flow and Transport in Porous Media. New Jersey, U.S.A.: Wiley. 258 p.         [ Links ]

Srivastava, R.; Jim-Yeh, T.C. (1991). Analytical Solutions for One-Dimensional, Transient Infiltration Toward the Water Table in Homogeneous and Layered Soils. Water Resources Research, 27(5), mayo, pp. 753-762.         [ Links ]

Terzaghi, K. (1943) Theoretical Soil Mechanics. New York, U.S.A.: John Wiley & Sons. 528 p.         [ Links ]

Van Genuchten, M.Th. (1980). A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44(5), agosto, pp. 892-899.         [ Links ]

Wu, L.Z.; Zhang, L.M. (2009). Analytical Solution to 1D Coupled Water Infiltration and Deformation in Unsaturated Soils. International Journal for Numerical and Analytical Methods in Geomechanics, 33(6), abril, pp. 773-790.         [ Links ]

Wu, L.Z.; Selvadurai, A.P.S. (2016). Rainfall Infiltration-Induced Groundwater Table Rise in an Unsaturated Porous Medium. Enviromental Earth Sciences, 75, pp. 1-11.         [ Links ]

Wu, L.; Zhang, L.; Li, X. (2015). One-Dimensional Coupled Infiltration and Deformation in Unsaturated Soils Subjected to Varying Rainfall. International Journal of Geomechanics, 16(2).         [ Links ]

Yang, H.; Rahardjo, H.; Leong, E. C. (2006). Behavior of Unsaturated Layered Soil Columns During Infiltration. Journal of Hydrologic Engineering, 11(4), junio, pp. 329-337.         [ Links ]

Yang, H.; Rahardjo, H.; Wibawa, B.; Leong, E. C. (2004). A Soil Column Apparatus for Laboratory Infiltration Study. Geotechnical Testing Journal, 27(4), pp. 347-355.         [ Links ]

Zhan, L.T.; Ng, C.W.W. (2004). Analytical Analysis of Rainfall Infiltration Mechanism in Unsaturated Soils. International Journal of Geomechanics, 4(4), diciembre, pp. 273-284.         [ Links ]