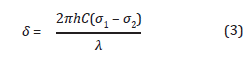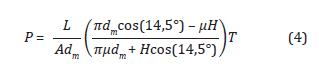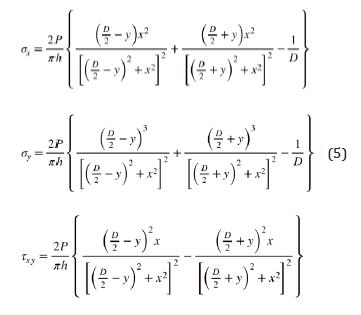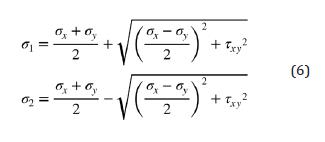1. INTRODUCCIÓN
Uno de los objetivos principales en los cursos de Mecánica de Sólidos, dentro del contexto ingenie-ril, radica en la apropiación de los métodos para la evaluación del campo de esfuerzos en cuerpos bajo solicitación mecánica. Este tipo de evaluaciones determina la forma en la que una fuerza se distribuye dentro del volumen del sólido, definiendo así la respuesta del material ante eventos de naturaleza mecánica (Hibbeler, 2011). Lo cual ha permitido a los ingenieros poder tomar decisiones asertivas en términos de la geometría de las estructuras, el tipo de material en ellas, y la identificación de los puntos donde se pueden intervenir, bien sea para la marcación de puntos críticos de falla, o para la remoción de material innecesario.
De manera convencional, los cursos de Mecánica de Sólidos son desarrollados desde una perspectiva conceptual, donde la evaluación del campo de esfuerzos es llevada a cabo para un número reducido de geometrías, desde un enfoque analítico y bajo la consideración, en su mayor parte, de solo los puntos críticos de un modelo. Estos casos usualmente corresponden a los puntos de concentración de esfuerzos. En estas perspectivas de trabajo, la caracterización de los valores de esfuerzo en los puntos críticos, se toma como criterio suficiente para la toma de decisiones en una etapa posterior de diseño (Budynas & Nisbett, 2012). Sin embargo, existen casos donde la evaluación de los esfuerzos de manera puntual no es suficiente, casos donde se requiere la construcción de un mapa de esfuerzos en campo completo. Chen et al., (2005) presenta un ejemplo de ello; al realizar un estudio mediante fotoelasticidad, en el cual prepone un modelo para identificar los puntos apropiados de perforación en estructuras para la ubicación de las tuberías.
Una forma de validar, contrastar y ampliar los componentes teóricos de la evaluación del campo de esfuerzos desarrollada de manera convencional en los cursos de Mecánica de Sólidos, está en la implementación de prácticas experimentales. No obstante, la integración de este tipo de prácticas, por su complejidad y sobre todo por la escasez de recursos, ha tenido una tendencia a ser evadida en los planes de estudio de este tipo de curso. Esto trae como consecuencia, que los estudiantes no se familiaricen con herramientas que pueden ser de utilidad para resolver situaciones ingenieriles en sus futuros profesionales. Por lo tanto, se hace necesario buscar la posibilidad de reforzar la forma convencional en la que se imparte la Mecánica de sólidos, a fin de llegar aproximaciones del mapa de esfuerzos a través de varios enfoques, como el numérico y el experimental, y en campo completo.
En relación a la evaluación del mapa de esfuerzos en campo completo, diversos trabajos han sido reportados en la literatura. Podría decirse que en una primera categoría se encuentran los métodos analíticos basados en la teoría de la elasticidad. En ellos, la distribución de esfuerzos es descrita a través de ecuaciones diferencias en una geometría definida, como se presenta en (Timoshenko & Goodier, 1951). Si bien los métodos analíticos permiten llegar a una aproximación de campo completo, la variedad de geometrías analizadas es muy reducida.
La segunda categoría identificada, se ubica en las técnicas numéricas (Métodos de Elementos Finitos MEF), las cuales trascienden de una opera-tividad manual a una operatividad computacional. Su aplicación, por lo general, consiste en el uso de paquetes informáticos que aproximan numéricamente la solución de las ecuaciones diferenciales comentadas en la categoría anterior (Dill, 2012). Este enfoque, aunque cuenta con extensa aplicación y aceptación (Dennis et al., 2011; Shetty et al., 2017; Kaminski y Fritzkowski, 2013), su utilización de manera independiente y exclusiva no brinda el estudiante la posibilidad de identificar factores experimentales y analizar los efectos de posibles cambios en las condiciones de carga o de geometría, que son escenarios subyacen en un contexto real.
Finalmente, en una tercera categoría, y atendiendo a trabajos recientes reportados en la literatura, la fotoelasticidad ha sobresalido como práctica experimental en la evaluación del mapa de esfuerzos en campo completo. Ello debido a que esta técnica no sólo es atractiva por su facilidad de visualización, sino porque permite la evaluación de la diferencia de esfuerzos principales y sus direcciones para esfuerzos inducidos o residuales, como es descrito en Doyle (2004).
Este trabajo integra la evaluación del mapa de esfuerzos en campo completo como estrategia de impacto en la forma convencional en la que suele ser impartido el curso de Mecánica de sólidos. Aquí, la evaluación del campo de esfuerzos se propone desde tres líneas de trabajo que conforman una estrategia experimental. Las líneas de trabajo consideradas incluyen la evaluación analítica del mapa de esfuerzos, la evaluación numérica-com-putacional, y la evaluación experimental utilizando fotoelasticidad, respectivamente. Cabe resaltar que la estrategia propuesta deviene de la aceptación que estudiantes de cursos previos en Mecánica de sólidos mostraron frente a la inclusión de este tipo de experimentos, y tiene como objetivo dotar a nuevos estudiantes, de herramientas para la solución de problemas ingenieriles comunes de un contexto real. Finalmente, en el trabajo se presenta la estrategia propuesta para integrar los tres métodos en la evaluación del mapa de esfuerzos en campo completo, se describe cada uno de los detalles de los experimentos, y se muestran los resultados del nivel de aceptación que los estudiantes tienen frente a la estrategia propuesta.
2. MARCO TEÓRICO DE FOTOELASTICIDAD
La fotoelasticidad es una técnica experimental para la evaluación del campo de esfuerzos en cuerpos birrefringentes bajo la aplicación de cargas mecánicas. Estas técnicas aprovechan el hecho que, al observar un cuerpo birrefringente a través de un montaje de polarización, la información referente a su campo de esfuerzos se hace evidente a través de la formación de patrones de franjas de color. Ello ha conllevado a que, de manera general, el principal objetivo contemplado en estudios de fotoelasticidad propenda por la recuperación de la información de los esfuerzos contenida en las intensidades de los patrones de franjas. (Baek, Kim & Hong, 2013; Magalhães, Magalhães & Magalhães, 2017; Alsiya et al., 2016).
En estudios de fotoelasticidad, los polariscopios varían en sus configuraciones dependiendo del tipo de aplicación (polarización lineal, circular o elíptica). En la Figura 1 se esquematiza el comportamiento de un rayo de luz que viaja a través de un polariscopio circular, el cual es implementado para analizar los esfuerzos de un disco bajo compresión diametral. De manera general, el fenómeno consiste en que la diferencia de esfuerzos principales en el cuerpo introduce un desfase de onda A de la luz que viaja, y su retardo de fase relativo S genera un cambio de intensidad de luz al emerger del polariscopio. Finalmente, la visualización del fenómeno desde todos los puntos del modelo es lo que genera la formación de los patrones de franjas de color. Hecht (2002) presenta una exposición más rigurosa sobre los fenómenos de luz polarizada, el efecto en elementos como polarizadores de luz, y el funcionamiento de los polariscopios.
Cabe anotar que, en montajes experimentales, la fotoelasticidad no sólo se realiza por transmisión de la luz; sino que también existen casos donde análisis de esfuerzos por reflexión han sido llevados a cabo. Para ello, se utilizan ciertos recubrimientos birrefringentes que se adhieren sobre las superficies de los modelos mecánicos. De este modo, el estado de deformaciones del modelo se transmite al recubrimiento, permitiendo evaluar su campo de esfuerzos a través de la formación de los patrones de franjas de color en el recubrimiento, (Ramesh, 2013). Otros autores han trabajado sobre aplicaciones de fotoelasticidad por reflexión, obteniendo la solución de diversos problemas mecánicos (Chang & Lien, 2007; Dubey & Grewal, 2010; Fernandes et al., 2003).
De manera puntual, el retardo de fase relativo 5 que da origen a la formación de los patrones de franjas de color, el cual está en función del espesor h del material, de sus índices de refracción n 1 y n 2 , y de la longitud de onda A de la fuente de luz, como queda expresado en la Ecuación (1). Además, en análisis mecánicos sobre materiales birrefringentes, la diferencia de los indicies de refracción está relacionada con la diferencia de esfuerzos principales (a - <J 2 ) y un coeficiente óptico del material C, como lo sugiere la Ley de esfuerzo óptico presentada en (2).
Al remplazar la Ecuación (2) en la Ecuación (1), se obtiene una expresión para el retardo relativo en función de la diferencia de esfuerzos principales, como se muestra en (3). Esta expresión resume la relación existente entre las propiedades mecánicas y ópticas de un material birrefringente bajo cargas mecánicas. En síntesis, el fenómeno óptico envuelve la información de los esfuerzos en cada punto del modelo.
Luego, al considerarse el arreglo óptico y la fuente de iluminación, se puede relacionar la intensidad de luz como función de la dirección de las componentes de esfuerzos principales y el retardo relativo. En Baek and Kim, (2005) se presentan expresiones de este tipo para diferentes arreglos ópticos. Esas expresiones evidencian que el retardo, que depende de la diferencia de los esfuerzos principales, modifica la intensidad de luz que emerge del polariscopio. De esta manera se puede decir que la información de los esfuerzos está contenida en la intensidad de la luz que emerge del polariscopio.
Inicialmente, muchos de los estudios en fotoelasticidad se basaban en el conteo de franjas, o en la comparación de colores utilizando la tabla de colores de interferencia de Michel-Levy (Ingham, 2012). Pero actualmente, con el desarrollo de las herramientas computacionales y de las cámaras digitales, ha surgido un enfoque en que se utilizan técnicas fundamentadas en el procesamiento digital de imágenes. Este enfoque, conocido como fotoelasticidad digital, parte del concepto de intensidad de pixel que es captada por una cámara (Briñez, Res-trepo-Martinez & Lopez, 2013).
3. MATERIALES Y MÉTODOS
Se realizó una evaluación cualitativa de la percepción de un grupo de estudiantes sobre el uso de la fotoelasticidad en las actividades de un curso de Mecánica de Sólidos de nivel de pregrado. A partir de las conclusiones de esta, se planteó la elaboración de una metodología para fortalecer los procesos de enseñanza de las temáticas del curso Mecánica de Sólidos en una forma convencional, que integrara enfoques analítico, numérico y experimental para la evaluación del mapa de esfuerzos en campo completo, la metodología propuesta se muestra en la Figura 2.
Para seguir la metodología, se diseñó un experimento para evaluar el campo de esfuerzos de un caso de estudio mediante fotoelasticidad. También, se desarrolló un modelo analítico basado en la teoría de la elasticidad y un modelo numérico de MEF del caso de estudio, que complementan a los análisis cualitativos y experimentales realizados mediante fotoelasticidad.
El caso de estudio que se utilizó corresponde a modelos con la geometría de un disco brasilero (Brazilian disc) sometido a cargas puntuales de compresión diametral; cuyo material birrefringen-te es Polimetilmetacrilato (PMMA) - comúnmente conocido como acrílico. El criterio de selección del caso de estudio obedeció al extenso uso de esta geometría en los estudios de fotoelasticidad (Ramakris-hnan & Ramesh, 2017; Lei, Yun & Kang, 2009; Zhang et al., 2012). La geometría, sus dimensiones y las propiedades del material del modelo son presentadas en la Tabla 1.
Análisis Cualitativo de Percepción
Se realizó sobre una muestra de 32 estudiantes a punto de culminar su curso de Mecánica de Sólidos en el pregrado de Ingeniería Mecánica de la Facultad de Minas de la Universidad Nacional de Colombia. La encuesta, que se realizó de forma personal, estuvo compuesta de dos preguntas con opciones de respuesta afirmativa o negativa. El análisis de los datos se hizo en términos porcentuales.
Modelo Experimental
El modelo experimental se basó en realizar una prueba mecánica de compresión sobre una probeta de PMMA y capturar una imagen de fotoelasticidad mediante un polariscopio circular. Así, el modelo experimental estuvo compuesto por un montaje mecánico para la prueba de compresión y un montaje óptico para captar la imagen.
En general los ensayos de compresión se realizan sobre máquinas especializadas, conocidas como maquinas universales. Estas generalmente son de alto costo y no son de fácil acceso. Sin embargo, en este estudio se utilizó un montaje mecánico de fácil aplicación e instrumentación accesible; esto con el fin de proponer un modelo experimental que puede ser replicado fácilmente en cualquier contexto académico o de diseño. El montaje estuvo equipado de un gato mecánico de tijera (Auto-Style, SKU 63378-X, Amsterdam, Países Bajos), al cual se le acopló una cabeza de tornillo hexagonal de 3/8" mediante soldadura, y un torquimetro de caratula (Snap-On, TEC 12A, Kenosha, Wisconsin, Estados Unidos) con precisión de 5 kg-cm (4,91x10-1 N-m).
Este montaje, que fue aplicado en el Laboratorio de Diagnostico de Maquinaria del Departamento de Ingeniería Mecánica de la Facultad de Minas de la Universidad Nacional de Colombia, consistió en la utilización del gato mecánico para levantar las probetas y comprimirlas contra una estructura de metal, como se muestra en la Figura 3 . De esa forma, se aprovechó el mecanismo anti-retorno del gato mecánico y la posibilidad de relacionar la carga compresiva con el torque que se aplica de manera controlada al tornillo de potencia del gato mecánico con un torquimetro. Cabe anotar que se utilizaron algunas placas de metal pulido entre el gato mecánico y la probeta para tratar de acercarse a la condición de aplicación de carga de manera homogénea en todo el espesor del disco.
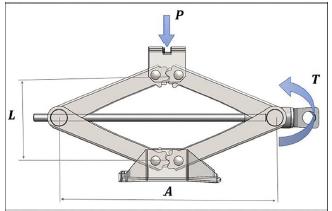
La relación para cuantificar la carga se encontró a partir de un análisis del equilibrio estático del gato mecánico. En este se hizo uso del modelo de carga transmitida por tornillos de potencia con rosca ACME propuesto por Budynas, & Nisbett (2008) en la sección de diseño de tornillos de potencia. Así, se encontró la expresión (4), que relaciona la carga P con las dimensiones L y A del gato mecánico, que se muestran en la Figura 4, el diámetro medio de rosca d m , el paso de rosca H y el coeficiente de fricción estático ¡x entre las superficies de la rosca del tornillo y la rosca interna de los collarines de empuje, en donde se acopla el tornillo con la estructura del gato mecánico.
En la Tabla 2 se presentan las mediciones y valores de referencia de los parámetros de la Ecuación (4) para el ensayo que se realizó y su método de medición o fuente de consulta.
El montaje óptico, por su parte, consistió de un polariscopio circular conformado por dos pola-rizadores lineales y dos retardadores de cuarto de onda, como se muestra en la Figura 5. Estos componentes fueron adquiridos de la línea de láminas plásticas ofrecida por Edmund Optics (Barrington, New Jersey, USA) con capacidad de transmisión del 90% para longitudes de onda entre 450-750[nm]. La captura de las imágenes se realizó con una cámara USB con captura a color (Edmund optics, High Definition Dual HDMI and USB Camera, Barrintong, New Jersey, USA). Como fuente de luz se utilizó una luz blanca LED con 200 de intensidad en escala de grises. La longitud de onda de esta fuente se toma como una aproximación de 560 [nm] correspondiente al valor medio de las longitudes de onda de luz que la componen.
Con este montaje se capturo una imagen digital en formato JPG que luego se procesó en MATLAB para cuantificar los valores de intensidad de luz en cada pixel y así poder realizar su comparación con el modelo analítico.
Cabe mencionar, que también se pueden visualizar imágenes de fotoelasticidad utilizando como primer polarizador (Antes de la probeta) una pantalla LED de algún computador o dispositivo electrónico y segundo polarizador (Después de la probeta) unas gafas para cine 3D. Ello es una opción de fácil acceso para experimentar con fotoelasticidad.
Modelo Analítico
Se implementó en MATLAB el modelo basado en la teoría de la elasticidad presentado por Jian-hong, Wu & Sun (2009) que describe en campo completo los esfuerzos para el caso de estudio en un sistema de referencia cartesiano XY cuyo origen está en el centro del disco. En las Ecuaciones (5) se presentan las expresiones analíticas para las componentes de esfuerzos normales en dirección de los ejes cartesianos (o x , o y ) y el esfuerzo cortante tangencial ( T iy ).
Donde P corresponde a la carga compresiva, D al diámetro y h al grosor de la probeta.
Estas componentes rectangulares, se transformaron a las componentes de esfuerzos principales, utilizando las expresiones de trasformación del circulo de Mohr, presentadas en las Ecuaciones (6).
Con el fin de realizar la comparación gráfica con el modelo numérico, se calcularon o 1 y o 2 con los valores de D y h de la Tabla 1 y un valor de carga P de 503 [N]. Posteriormente, se graficaron los valores de o 1 y o 2 de un conjunto de 513x513 pares cartesianos en representación de pseudo-colores.
Por otro lado, para la comparación con el modelo experimental, se calculó la diferencia entre las componentes de esfuerzos principales (a - o 2 ) y la dirección 6 en que estas se presentan (Hibbeler, 2011). Ello para un valor de carga igual al utilizado en la experimentación (P = 325,38 [N]). A partir de los valores de (a 1 - a 2 ) y de la expresión (3) con un valor A de 560 [nm] y los valores h y C de la Tabla 1, se obtuvo el mapa de retardo de fase relativo ó. Luego, se utilizó la expresión de intensidad de luz propuesta por Shang, Ji & Yang (2015) para calcular los valores de intensidad de luz I de una imagen a fondo gris a partir de un arreglo óptico de polarización circular; presentada en la Ecuación (7).
Donde /B corresponde a la intensidad de la luz ambiente o de ruido(Que se estableció igual a 40), mientras que /f corresponde a la intensidad de luz de la fuente (200). A partir de los valores de intensidad calculados de la Ecuación (7) se generó una imagen sintética de fotoelasticidad de 513x513 pixeles.
Modelo Numérico
Una representación 3D de CAD de la geometría en análisis se desarrolló en SOLIDWORKS. A partir de esta se realizó el modelo del MEF utilizando el paquete de software ANSYS R15.0. La malla del modelo, que se presenta en la Figura 6, fue una de elementos tetraédricos compuesta por 156754 nodos y 77405 elementos. La selección del mallado obedece a que éstas condiciones generalmente satisfacen de manera efectiva los criterios de convergencia y suponen una elección apropiada para obtener soluciones precisas (Doyle, 2004).
Las condiciones de carga se establecieron de manera que replicasen los supuestos del modelo analítico (valor de 503[N] y aplicación puntual de manera diametralmente opuesta). Para ello, se pa-rametrizó la carga aplicada como una distribución uniforme sobre todo el grosor del disco y con un ancho de 3,99 [mm], que corresponde a solo el 0,03% del perímetro de este; lo cual permite aproximar con exactitud la condición de aplicación de carga puntual. Además, se utilizó la condición de equilibrio estático, en conjunto con la configuración de ambas cargas en una misma línea de acción, para garantizar la oposición diametral de éstas.
El modelo se desarrolló como un caso de material isotrópico elástico-lineal. Los parámetros de módulo elástico y coeficiente de Poisson se asignaron con los valores de la Tabla 1. El tiempo de cómputo para la solución del modelo MEF estuvo entre 45 segundos y 65 segundos en un computador con una unidad de procesamiento típica de tres núcleos de 64 bits y memoria RAM de 3 GB.
4. RESULTADOS Y DISCUSIÓN
Análisis Cualitativo de percepción
En la Figura 11, se presentan los resultados que se obtuvieron de la encuesta sobre la muestra de estudiantes que anteriormente se definió. A estos se les solicitó responder de manera afirmativa o negativa a las siguientes preguntas:

Figura 11 Resultados de la encuesta de percepción sobre la utilización de la fotoelasticidad en los procesos de enseñanza y diseño en la Mecánica de Sólidos
Pregunta 1: ¿Fue el uso de la fotoelasticidad útil para el desarrollo de las actividades del curso y en general para su formación en los temas tratados en su curso de Mecánica de Sólidos?
Pregunta 2: ¿Consideraría utilizar la fotoelasti-cidad en alguna actividad futura relacionada con los temas asociados a la Mecánica de Sólidos?
La Figura 11A muestra que la percepción de los estudiantes es que la fotoelasticidad les fue útil durante su formación en la Mecánica de Sólidos. Mientras que la Figura 11B, muestra que estos consideran la fotoelasticidad como una herramienta a ser utilizada en futuras actividades que impliquen el análisis de los temas asociados a la Mecánica de Sólidos.
Comparación: Modelo Numérico -Modelo Analítico
En la Figuras 7 y 8 se presentan los resultados obtenidos para las componentes de esfuerzo principal máximo (oj y mínimo (<j 2), respectivamente. Allí, se presentan las representaciones de la solución en campo completo a partir de los enfoques numérico (Figuras 7A y 8A) y analítico (Figuras 7B y 8B).
Estas representaciones están en una escala de colores que el software ANSYS asigna por defecto a algunos valores representativo del intervalo de esfuerzos calculados. La misma escala se asignó en la representación de los resultados del modelo analítico con el fin de facilitar el proceso comparativo.
De las Figuras 7 y 8 se evidencia la consistencia entre los mapas de esfuerzos de las componentes de esfuerzos principales a partir de ambos enfoques. En esas gráficas se detalla que tanto las magnitudes como las distribuciones de los esfuerzos coinciden entre los dos modelos. La Figura 7, por ejemplo, muestra que ambos enfoques predicen que se genera una región hacia el centro del disco, donde los valores de esfuerzo principal máximo o 1 son los mayores y tiene como valor representativo a 3,3599x105 Pascales. Por su parte, la Figura 8 muestra como los dos enfoques predicen que sobre las regiones en cercanía a los puntos de aplicación de las cargas, los valores del esfuerzo principal mínimo o2 crecen rápidamente hasta sus valores máximos sobre las regiones representadas en azul.
No se debe permitir la confusión por los colores de la región por fuera del disco en las representaciones de los resultados analíticos (Figuras 7b y 8b), estos colores corresponden a los valores cero de esfuerzos en la escala de colores.
Con base en el análisis anterior, se llega a que se presentó uniformidad entre los resultados de los modelos numérico y analítico; por lo cual se establece que estos modelos de referencia son apropiados para la validación.
Comparación: Modelo Analítico - Modelo Experimental
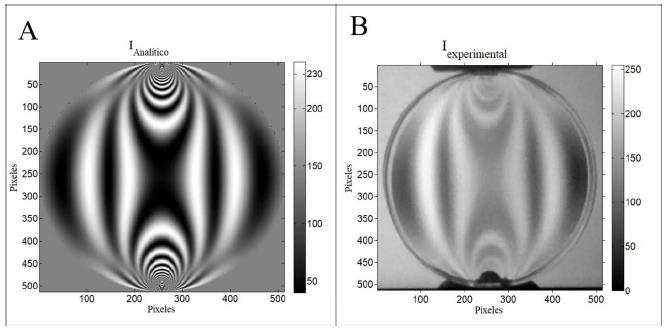
En la Figura 9 se presenta la imagen comparativa para los valores de intensidad de luz /, a partir de los enfoques analítico y experimental. En la Figura 9A se presenta la imagen sintética generada a partir de los valores de intensidad de luz calculados en MATLAB del modelo analítico; y en la Figura 9B se presenta la imagen digital que se capturó del experimento del modelo experimental y posteriormente se procesó en MATLAB para pasarla a escala de grises y cuantificar la intensidad de luz en cada pixel.
La representación en escala de grises es con el fin de hacer más gráfica su comparación y ante la dificultad de poder establecer en MATLAB la escala de colores real que es captada por un observador en un experimento de fotoelasticidad.
La Figura 9 muestra como las imágenes sintética y experimental tienden a tener patrones de franjas similares sobre todo el disco. Sin embargo, se presentaron divergencias entre los tonos de las franjas y sus resoluciones.
Ante esos casos, las diferencias de intensidades pueden ser atribuidas tanto a las fuentes de iluminación consideradas para la generación de estas imágenes, como a la variabilidad experimentales del valor de luz ambiente o de ruido. Ejemplo de ello fue que en la imagen sintética la máxima intensidad se dio a los 240 en escala de grises, y la máxima intensidad para la imagen experimental alcanza los 255 en escala de grises. También, se pueden obtener mayor homogeneidad entre los resultados si se mide el coeficiente óptico del material de las probetas, pues se puede dar que este valor no coincide de manera aproximada al valor de referencia aquí utilizado. Otros factores que pudieron tener influencia en las divergencias presentadas, son la suposición hecha para la longitud de onda de la luz blanca utilizada y posibles variaciones en la trasmisión de la luz por pate de los elementos ópticos del polariscopio. Adicionalmente, se debe tener en cuenta, que posibles variaciones del valor de carga aplicada, con respecto al calculado a través de la expresión (4), se pueden presentar por el carácter experimental del ensayo mecánico.
A pesar de las divergencias, se puede establecer que existe consistencia entre los patrones de franja de fotoelasticidad de los modelos analítico y experimental. Lo que a su vez, también define la consistencia entre la evaluación de los mapas de esfuerzos a partir de ambos enfoques.
De esa forma, se da lugar a la validación del uso de la fotoelasticidad para la evaluación del campo de esfuerzos, a través de la comparación de sus resultados con métodos analíticos y modelos numéricos.
Con el objetivo de mostrar el patrón de franjas que realmente se observó durante la experimentación, en la Figura 10 se presenta la imagen de fotoelasticidad originalmente capturada.
5. CONCLUSIÓN
En el desarrollo de este documento, se presentó una evaluación cualitativa que muestra como la fotoelasticidad es percibida de forma aprobatoria para la formación en Mecánica de Sólidos y es considerada como una herramienta a ser utilizada a futuro por los estudiantes de un curso de Mecánica de Sólidos. Con ello como referencia, se propuso una metodología de implementación de la fotoelasticidad en cursos de mecánica de sólidos de nivel de pregrado, que integra enfoques analítico, numérico y experimental.
Para ello, se propuso un experimento para evaluar el campo de esfuerzos de un disco bajo compresión diametral. Además de evaluarse un modelo analítico basado en la teoría de la elasticidad y un modelo numérico de MEF de este caso de estudio. Con los resultados de estos modelos se realizó un análisis comparativo de resultados que condujo a la validación del uso de la fotoelasticidad como herramienta para los cursos de Mecánica de Sólidos.
De esa forma, se estableció un resultado que replantea la forma convencional en que se realizan los procesos de aprendizaje-enseñanza de la Mecánica de Sólidos.