1. Introducción

Las nanoestructuras semiconductoras (pozos cuánticos, hilos cuánticos, superredes y puntos cuánticos, etc) han tenido un interés considerable en estudios teóricos y experimentales gracias a la gran variedad de aplicaciones en dispositivos electrónicos y optoelectrónicos ^{Gil, et al. (2017)}. Algunas aplicaciones incluyen, entre otras, los láseres semiconductores de estado sólido ^{Lelong y Bastard (1996)}, amplificadores ópticos, fotodetectores en el infrarojo, y láseres de cascada cuántica ^{Kanyinda y Cruz (2003)}; Yiming, et al. (2001). Con los avances en la síntesis de sistemas semiconductores de baja dimensionalidad, se ha hecho posible fabricar una amplia variedad de puntos cuánticos, conocidos como átomos virtuales dado el carácter discreto de su espectro de energía. Entre las técnicas para la fabricación de puntos cuánticos se encuentran la epitaxia de haces moleculares y la bien conocida Stranski-Krastanov, mediante la cuales es posible obtener puntos cuánticos de diferentes formas tales como pirámides y lentes, entre otras ^{Lelong y Bastard (1996)}; ^{Iqraoun, et al. (2017)}. Además de las diferentes formas geométricas, se ha encontrado que los campos eléctricos y magnéticos, la radiación láser intensa no resonante, la presión hidrostática, y la temperatura modifican las propiedades electrónicas y ópticas de tales sistemas de dimensión cero ^{Hiruma, et al. (2006)}; ^{Avazzadeh, et al. (2016)}; ^{Iqraoun, et al. (2017)}. Una gran variedad de estudios se ha dedicado también a los efectos de la presencia de impurezas ^{Hiruma, et al. (2006)}; ^{Ngo, et al. (2006)}.

Para el caso particular de un punto cuántico en forma de cono se han realizado muchos estudios, entre ellos: i) la generación de segundo y tercer armónico, ii) efectos de la posición de impureza sobre los niveles de energía, iii) el cálculo de la susceptibilidad diamagnética de una impureza donadora hidrogenoide descentrad y iv) los efectos simultáneos de un campo eléctrico externo y la posición de impurezas sobre la rectificación óptica no lineal ^{Gil, et al. (2017)}; ^{Hiruma, et al. (2006)}; ^{Lelong y Bastard (1996)}; ^{Avazzadeh, et al. (2016)}; Yiming, et al. (2001). Igualmente, se ha investigado teóricamente la absorción óptica relacionada con impurezas donadoras, los cambios relativos del índice de refracción y la dispersión Raman. Los investigadores han concluido que, por ejemplo, los cambios relativos del índice de refracción siguen la misma tendencia que el coeficiente de absorción ^{Niculescu, Tiriba, y Spandonide (2015)}; ^{Rezaei, Karimi, y Pakarzadeh (2013)}. Se han presentado reportes acerca de las propiedades ópticas lineales y no lineales de tercer orden de puntos cuánticos cónicos con potencial de barrera infinito. Particularmente, se han calculado los coeficientes de absorción lineal, no lineal y total, así como los índices de refracción de los puntos cónicos de GaAs teniendo en cuenta los efectos del tamaño y formas y de un campo electromagnético incidente ^{Dezhkam, y Zakery (2012)}; ^{Khordada y Bahramiyanb (2014)}.

En esta investigación hacemos un estudio teórico de las propiedades electrónicas y ópticas de puntos cuánticos de GaN en forma de sector cónico esférico (PCSCE). Presentamos el espectro electrónico y algunos ejemplos de las funciones de onda de los estados más bajos de energía. Teniendo esto como información, procedemos a calcular los elementos de matriz de dipolo para transiciones entre niveles de energía y finalmente reportamos los coeficientes de absorción óptica e índice de refracción. El artículo está distribuido en la siguiente forma: en la sección II presentamos el marco teórico, la sección III está dedicada a los resultados junto a su correspondiente discusión y finalmente, en la sección IV se reportan las conclusiones.

2. Marco teórico

La Figura 1(a) ilustra la manera en que se construyó la geometría del PCSCE. Los valores de parámetros físicos usados corresponden al GaN. En dos dimensiones se construyó un sector circular cuyo ángulo de apertura θ ₀ y radio r₀ son controlables para tener en cuenta los efectos geométricos y de forma sobre las propiedades electrónicas y ópticas. Para modelar un confinamiento infinito en los bordes, se impusieron condiciones tipo Dirichlet las cuales implican que la función de onda se anula en las fronteras del punto cuántico. Se construye entonces la región sombreada en gris y se genera un sólido de revolución mediante un giro de 360° alrededor del eje z, lo cual resulta en un sector cónico esférico, tal como el que ha sido representado en una vista 3D en la Figura 1(b).

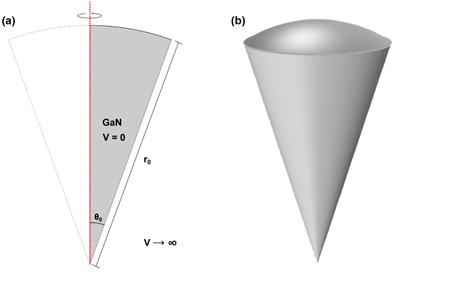
Figura 1 Proyección en el plano y = 0 de un punto cuántico de GaN en forma de sector cónico esférico con potencial de confinamiento infinito, ángulo de apertura θ ₀ y radio r₀. Este sector se hace girar al rededor del eje z para generar un punto cuántico con geometría de sector cónico esférico (a). Representación esquemática del punto cuántico de GaN en forma de sector cónico esférico (b). 

Consideremos un electrón confinado en el PCSCE de GaN. En la aproximación de masa efectiva y usando coordenadas cilíndricas, el Hamiltoniano del sistema es:

donde m _e ^* es la masa efectiva electrón para GaN, y V(r, z) el potencial de confi namiento, el cual tiene la forma:

Las energías y funciones de onda de los estados ligados se obtienen mediante la ecuación de Schrödinger:

En consideración que nuestro problema tiene simetría azimutal, la función de onda ¥(r, z, (b) puede ser escrita en la forma:

donde I es un número entero. Sustituyendo la Ecuación (4) en la Ecuación (3) y haciendo uso del Hamiltoniano en la Ecuación (1), obtenemos

La solución a la ecuación diferencial (1) se implementa mediante el método de elementos finitos haciendo uso del software licencia COMSOL-Multiphysics. En este caso particular, dada la simetría azimutal del problema, hacemos uso del módulo eje simétrico del mencionado software.

Un segundo grupo de resultados corresponde a propiedades ópticas del punto cuántico. En este trabajo se calculan los aportes lineales del coeficiente de absorción óptico y de los cambios relativos del índice de refracción, dados respectivamente por las siguientes dos ecuaciones ^{Nguyen, et al. (2017)}.

donde ℏω es la energía de fotón incidente, μ es la permeabilidad magnética del vacío, ε _R = ε ₀ ε es la parte real de la permitividad (ε ₀ es la permitividad del vacío y ε es la constante dieléctrica del GaN), e es la carga del electrón, ρ _jl es la diferencia de concentración de electrones entre los niveles j y l, Γ _jl es una tasa de relajamiento pro veniente de la fenomenología, E _jl es la energía de transición entre los niveles j y l, M _jl = 〈j│z│l〉 es el elemento matricial de transición entre los niveles j y l con polarización en dirección z y n el índice de refracción del GaN.

3. Resultados y discusión

En este trabajo se tomaron los parámetros señalados en la teoría con los siguientes valores: μ = 4π x10^-7, ε ₀ = 8.85 x10^-12 F/m, ε = 13, e = 1.6 x 10^-19 C, ρ = 3.0 x 10²² m^-3, Γ = 15 x10¹² s^-1 y n = 3.61.

Figura 2 Energía de los primeros diez estados ligados de un electrón confinado en un punto cuántico de GaN, en forma de sector cónico esférico, como función del radio de la estructura r₀. Los resultados corresponden a θ ₀ = 20° con l = 0 (a) y l = 1 (b). 

En la Figura 2 se muestran las energías de los primeros diez estados del electrón confinado en un PCSCE de GaN como función del radio de la estructura r₀. Los resultados corresponden a θ ₀ = 20°, tomando dos valores para el número cuántico l: l = 0 (a) y l = 1 (b). Las energías del electrón son decrecientes con el aumento del radio del cono, lo cual se explica por la pérdida del confinamiento al aumentar el volumen estructural. Al mantener constante el ángulo θ ₀ , el sector circular tiene una mayor área con el aumento de r₀, lo que genera a su vez un mayor volumen de revolución, dando como resultado un menor confinamiento para un portador de carga. Esta descripción del comportamiento del volumen como función del ángulo θ ₀ y el radio r₀ puede escribirse analíticamente como:

En la Figura 2(a) no hay presencia de degeneraciones por el tipo de simetría que exhiben las funciones de onda para l = 0. Si organizamos el espectro en orden ascendente, teniendo en cuenta los diferentes valores de l, vemos por ejemplo, que para los estados estudiados en esta figura: Si r₀ = 5 nm, en (a) el estado fundamental está representado en color negro (l = 0), el primer estado excitado está en 2(a) en color rojo y el segundo estado excitado está en negro en 2(b) para l = 1 (este estado es degenerado pues tiene la misma energía que el correspondiente a l = -1). La evidencia de un comportamiento similar de los espectros de energía como función de r₀, para dos valores distintos de l, indica la aparición de diferentes espectros correspondiente a cada valor de l. De manera que el conocimiento del espectro en su totalidad, usando un modelo bidimensional para el punto cuántico, proviene de la simetría azimutal. Una mayor densidad de niveles por unidad de energía ocurre para l = 0. El surgimiento de degeneración accidental para un estado excitado, etiquetado con el número 2 en 2(b), ocurre por la inversión de simetría de los estados y para el ángulo θ ₀ = 20°.

En la Figura 3 se observan las proyecciones en el plano 0 = 0 de funciones de onda de los tres primeros estados confinados de un electrón un un PCSCE de GaN con 9 ₀ = 20 ° y R = 10 nm. En la Figura 3(a), se evidencia que para / = 0, los estados tienen simetría tipo s, y los dos primeros estados excitados *¥₂ y ¥₃ poseen uno y dos antinodos en dirección vertical, respectivamente. Para / = 1, Figura 3(b), se observa un patrón similar que en Figura 3(a), pero las funciones de onda no son simplemente conectadas a través del ángulo de giro (forma de anillos). Al comparar ¥₁, ¥₂ y ¥₃, en ese orden, se evidencia que los estados excitados del electrón tienen una mayor expansión sobre el punto cuántico, alcanzando regiones de mayor confinamiento. Los colores en la Figura 3 tienen la siguiente interpretación para los valores de la función de onda: i) verde corresponde a un valor cero, ii) rojo al valor máximo positivo y azul al valor máximo negativo de la función de onda, iii) valores intermedios están dados por las otras tonalidades presentes en la figura. El comportamiento de las funciones de onda para los demás valores tomados en este trabajo 5 nm < R < 10 nm, muestran un mismo patrón de comportamiento.

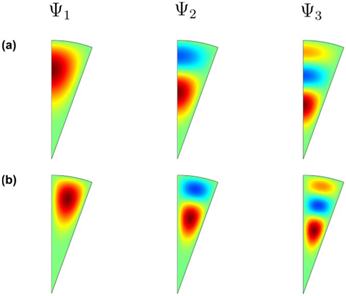
Figura 3 Proyección en el plano ϕ = 0 de las funciones de onda para los tres primeros estados confinados de un electrón en un punto cuántico de GaN, en forma de sector cónico esférico. Los resultados a lo largo de las filas corresponden a θ ₀ = 20° y r₀ = 10 nm con l = 0 para la primera fila (a) y l = 1 para la segunda fila (b). 

La Figura 4 muestra el cuadrado de los elementos de matriz de dipolo para dife rentes transiciones entre niveles de un electrón confinado en un PCSCE de GaN (aquí se considera el momento de dipolo reducido, es decir, el momento de dipolo eléctrico dividido por la carga del electrón). Específicamente, se han calculado todas las combi naciones posibles entre los dos primeros estados, (i =1,2) y los primeros diez estados excitados (j = 2, 3,...,10), en función del radio r ₀ de la estructura. Los resultados son para θ ₀ = 20° y se usa un láser resonante polarizado linealmente en dirección z, con l = 0 en Figura 4(a) y l = 1 en Figura 4(b). Se observa que tanto en la Figura 4(a) como en 4(b), solo las transiciones Ψ₁→Ψ₂ y Ψ₂→Ψ₃ son dipolarmente permitidas. Esto se explica en términos de las condiciones de simetría de las funciones de onda. Por ejem plo, para el elemento matricial M _z ^1,2 ≠ 0 con l = 0, Ψ₁ es una función par respecto al cen tro de gravedad del PCSCE de GaN, mientras que Ψ₂ es una función aproximadamente impar, lo cual resulta en un valor diferente de cero para el elemento de matriz dipolar. Del mismo modo se explican las transiciones Ψ₂→Ψ₃, con Ψ₃ siendo una función par con respecto al centro de gravedad. Las transiciones permitidas en estas figuras son favorecidas por un radio mayor del sector esférico, lo cual se manifiesta en un com portamiento monótono creciente. Note que para los valores tomados de ro se cumple la desigualdad M _z ^2,3 > M _z ^1,2, ya que la región de superposición de las funciones de onda Ψ₂, con Ψ₃ es mayor. El comportamiento de los elementos matriciales para l = 0 y l = 1 muestra un patrón similar ya que la simetría de las funciones de onda para cada nivel correspondiente se mantiene, tal como se observa en la Figura 3. Las transiciones permitidas para cada espectro son entre los mismos pares de niveles, ya que tenemos una misma paridad para las funciones de onda en cada caso.

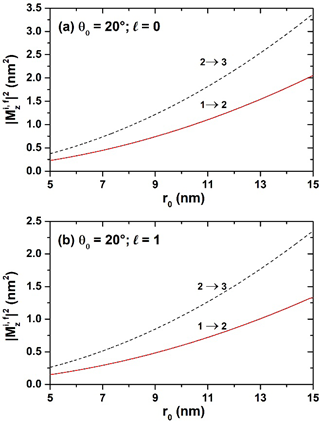
Figura 4 Cuadrado de los elementos de la matriz de dipolo para diferentes transiciones entre niveles de un electrón en un punto cuántico de GaN, en forma de sector cónico esférico, en función de r₀. Los resultados corresponden a θ ₀ = 20° con l = 0 (a) y l = 1 (b). Se usa un láser resonante polarizado linealmente en dirección z. 

En la Figura 5 se muestran los coeficientes ópticos en función de la energía del fotón incidente para valores de radio del sector esférico r₀ entre 5.0 nm y 15 nm. El coeficiente de absorción óptica, en la Figura 5(a), presenta un corrimiento hacia el rojo (disminución de la energía donde se localiza la estructura resonante) con el aumento del radio r₀ del sector esférico. Note que, dentro de las transiciones estudiadas en este trabajo, solo aparecen como permitidas dos de ellas. La transición Ψ₁→Ψ₂, de menor energía presenta una menor absorción en comparación con la transición Ψ₂→Ψ₃ que hace un mayor aporte a la absorción. Para los valores más grandes de r₀, los picos de absorción alcanzan a superponerse por la menor diferencia entre las energías de transiciones, esto es, para valores más grandes de r₀ la densidad de niveles de energía es mayor, tal como se muestra en la Figura 2. Desde el punto de vista de trabajos experimentales, para determinar el aporte de varias transiciones a la absorción sería necesario el cálculo de una deconvolución sobre los resultados obtenidos. En la Figura 5(b) el cambio del índice de refracción tiene dos máximos alrededor de cada pico de absorción (que corresponde aproximadamente a la posición del cero del índice de refracción). Para los valores más grandes del radio del cono hay dos picos de cambio en el índice de refracción claramente diferenciados con respecto a los que se observan para los radios más pequeños. El comportamiento de cambio de índice de refracción con dos máximos alrededor del valor donde ocurre la mayor absorción (realmente un máximo a la izquierda y un mínimo a la derecha) se le denomina región de dispersión anómala ^{Çakir, Yakar, y Özmen (2012)}.

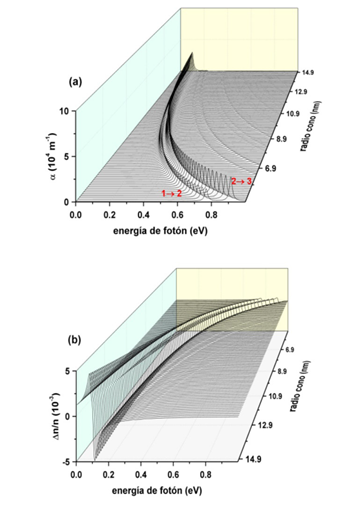
Figura 5 Coeficientes ópticos para el punto cuántico de GaN, en forma de sector cónico esférico. Coeficiente de absorción óptica como función de la energía de fotón incidente para radios del sector esférico entre 5 nm y 15 nm (a); cambios del índice de refracción como función de la energía de fotón incidente, para varios valores de radio del sector esférico r ₀. Para estas propiedades se fijó l = 0. 

En la Figura 6 se muestran las energías de los primeros diez estados de un electrón confinado en un PCSCE de GaN en función del ángulo θ ₀. Se fija el radio en r₀ = 10 nm con l = 0 (a) y l = 1 (b). En esta figura se observa que al aumentar el ángulo se produce un comportamiento general de decrecimiento de las energías, para los diferentes estados, como resultado de la disminución en el confinamiento, lo cual es modelado mediante la Ecuación (10). La mayor pendiente de las curvas para l = 1, Figura 6(b), en comparación con l = 0, Figura 6(a), se debe a que en el primer caso los estados están más extendidos en el punto cuántico, lo cual hace que sean más sensibles a los cambios geométricos. La aparición de cruces para los niveles excitados se explica por el intercambio de simetrías entre ellos. Es importante señalar que para la Figura 6(a), las degeneraciones que aparecen, corresponden solo a los puntos de cruces de las curvas, es por tanto, una degeneración doble de tipo accidental. En contraste para la Figura 6(b) todos los estados presentan degeneración doble por la condición de simetría azimutal (los estados con l =-1 corresponden a un espectro idéntico al mostrado para l = 1). Los puntos de cruce de las curvas, corresponden entonces a degeneración cuádruple. Por otro lado, los cruces accidentales para los estados de mayor energía ocurren para estructuras cada vez de mayor volumen, esto es, el ángulo para el cual ocurre el intercambio de simetría aumenta, como se observa para ambos paneles [Figuras. 6(a) y 6(b)].

Figura 6 Energía de los primeros diez estados ligados de un electrón confinado en un punto cuántico de GaN, en forma de sector cónico esférico, en función del ángulo θ ₀, para r₀ = 10 nm con l = 0 (a) y l =1 (b).  

En la Figura 7 se reporta el cuadrado de los elementos de la matriz de dipolo para diferentes transiciones entre niveles de un electrón confinado en un PCSCE de GaN en función del ángulo θ ₀, para r ₀ 10 nm con l = 0 (a) y l = 1 (b). Se usa un láser resonante polarizado linealmente en dirección z. Se puede apreciar que para un án gulo aproximado de 30° ocurre un intercambio de simetría entre los niveles Ψ₂→Ψ₃ y Ψ₂→Ψ₄. Una condición similar ocurre para las transiciones Ψ₁→Ψ₃ y Ψ₁→Ψ₄ para ese mismo ángulo, la diferencia a remarcar para estas dos transiciones es que, para ángu los pequeños, ambas transiciones son prácticamente cero. Con el aumento del ángulo aparecen valores diferentes de cero para la transición Ψ₁→Ψ₃. Este incremento en el valor del elemento matricial para las transiciones permitidas se alcanza por el mayor solapamiento entre las funciones de onda de los estados involucrados en la transición, ya que los diferentes estados son más extendidos en la estructura por ser de mayor volumen, conforme se aumenta el ángulo. Como se observa para la Figura 6(a) de energías, la transición Ψ₁→Ψ₂ mantiene un comportamiento monótono, sin intercambio con otras transiciones, ya que no se cruza con otros niveles. La Figura 7(b), con valor de l = 1, exhibe un comportamiento análogo al de la Figura 7(a), con valores de elementos matriciales ahora dependientes sobre funciones de ondas localizadas radialmente y que forman un ángulo con el eje z, contrario a la Figura 7(a) donde las funciones de onda forman figuras solidas (sin huecos, que generan formas tipo anillo) en la simetría azimutal (ver Figura 3).

Figura 7 Cuadrado de los elementos de la matriz de dipolo para diferentes transiciones entre niveles de un electrón confinado en un punto cuántico de GaN, en forma de sector cónico esférico, en función del ángulo θ ₀, para r₀= 10 nm con l = 0 (a) y l = 1 (b). Se usa un láser resonante polarizado linealmente en dirección z. 

La Figura 8 muestra la influencia del cambio en el ángulo, sobre las funciones de onda de los estados electrónicos en un PCSCE de GaN que pasa de un ángulo apical de 20°, Figura 8(a), a un ángulo apical de 60°, Figura 8(b). La forma de los dos primeros estados se mantiene, la diferencia está en el confinamiento en cada estructura, en la Figura 8(a) las funciones de onda tienen una región más amplia de localización. Tal como se observa para las energías en la Figura 7, hay un intercambio de simetría entre los estados Ψ₃ y Ψ₄. De ahí que para el tercer estado mostrado en la Figura 8, para los dos ángulos escogidos, no se tenga la misma simetría.

Figura 8 Funciones de onda de los tres primeros estados ligados de un electrón confinado en un punto cuántico de GaN, en forma de sector cónico esférico, para r₀ =10 nm con l = 0 para la primera fila y l = 1 para la segunda fila, correspondiente a dos ángulos θ ₀=20° (a) y θ ₀= 60° (b). 

En la Figura 9 se muestran los coeficientes ópticos en función del ángulo del sector esférico. En la Figura 9(a) el coeficiente de absorción presenta un corrimiento hacia el rojo con el aumento del ángulo del sector esférico. Los picos correspondientes a las transiciones Ψ₁→Ψ₂ y Ψ₂→Ψ₃ (o Ψ₂→Ψ₄, dependiendo del valor de θ ₀) se define con claridad en la gráfica. La absorción como resultado de la transición Ψ₁→Ψ₂ es más débil.

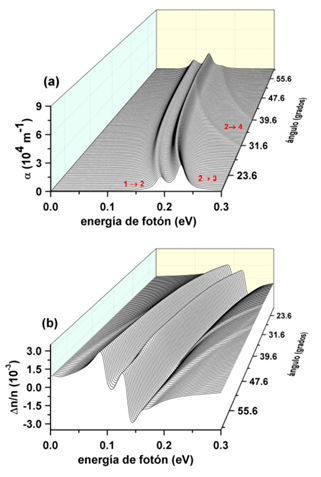
Figura 9 Coeficientes ópticos para el punto cuántico de GaN, en forma de sector cónico esférico. Coeficiente de absorción óptica (a) y cambios del índice de refracción (b) como función del ángulo apical del sector esférico y de la energía de fotón resonante. Para estas propiedades se fijó l = 0. 

No existe superposición de las regiones de absorción, por lo que no hay reforzamiento de la absorción como ocurrió para el caso de la Figura 5. La transición Ψ₁→Ψ₃, que corresponde a un valor de elemento de transición diferente a cero, de acuerdo con la Figura 7, tiene valores de absorción casi imperceptibles. Dos regiones anómalas en la Figura 9(b) aparecen en correspondencia con las regiones de mayor absorción en la Figura 9(a). Al comparar las propiedades ópticas de las Figuras 5 y 9, se aprecia que el favorecimiento de mayores cambios en el índice de refracción se alcanza con el cambio del radio del cono, esto es, Figura 5(b). Los radios mayores tomados en este trabajo, alrededor de 15 nm, favorecen una mayor absorción.

4. Conclusiones

En este artículo se han reportado las propiedades ópticas y electrónicas de un electrón confinado en un punto cuántico de GaN, en forma de sector cónico esférico. Los cálculos se han hecho en la aproximación de masa efectiva empleando el método de elementos finitos para resolver las ecuaciones diferenciales del problema. Dada la simetría azimutal del problema, la ecuación diferencial 3D se reduce a una ecuación diferencial 2D en coordenadas cilíndricas. Se emplean las condiciones de Dirichlet para garantizar la nulidad de la función de onda en las paredes del punto cuántico. Se han reportado el coeficiente de absorción y el de cambios relativos en el índice de refracción. El estudio demuestra que elecciones adecuadas del ángulo apical y del radio del punto cuántico pueden dar origen a magnificaciones en las propiedades ópticas. Corrimientos al rojo de las estructuras resonantes de las propiedades ópticas se asocian claramente con el aumento tanto del ángulo apical como del radio de la estructura.