Introducción
Al ser el hurto un delito de tipo monetario es razonable pensar que puede estar relacionado con indicadores económicos que reflejen las condiciones de inversión social y calidad de vida en los municipios. Este hecho ha sido estudiado por Sandoval y Barón (2008), quienes argumentan que el crimen depende de las oportunidades a las que se tenga acceso en la sociedad y que incentiven el desarrollo personal y económico de los individuos que les permita satisfacer sus necesidades básicas.
Según los datos reportados por el observatorio del delito de la Policía Nacional de Colombia, desde el año 2003, en Colombia se ha presentado una tendencia al incremento en el hurto a personas (Norza et al., 2017). Dicho comportamiento impulsa la realización de investigaciones que ayuden a entender el contexto en el que ocurren los delitos y los principales factores socioeconómico-demográficos asociados con el crimen para poder entender las causas directas e indirectas que propician la actividad delincuencial.
Teniendo en cuenta la heterogeneidad del territorio nacional (Castillo, 2007) -diferencias de tipo cultural, social y económico-, se espera que existan variaciones significativas en las estadísticas criminales entre municipios que no puedan ser explicadas adecuadamente por un modelo de regresión lineal múltiple global. Por esta razón en este trabajo se utilizará la técnica de regresión ponderada geográficamente (GWR por sus siglas en inglés) (Brunsdon, Fotheringham y Charlton, 1996), en la que se pueden identificar variaciones espaciales entre el hurto y las variables explicativas a partir de la variación de los coeficientes del modelo. Dichos modelos pueden contribuir a la planificación de políticas públicas, adecuadas al contexto de cada municipio, y que pueden ser promovidas por las diferentes entidades gubernamentales que podrían tener impacto en el aumento o disminución de los índices de criminalidad.
En este trabajo se compara un modelo de regresión lineal múltiple y un modelo GWR mediante el uso tanto del coeficiente de determinación ajustado (Ra 2) como de los Criterios de Información de Akaike (AIC) y el criterio de información bayesiano (BIC).
Marco teórico
Relación entre el crimen y las condiciones socioeconómicas
Sandoval y Barón (2008, p. 105) analizaron la situación actual de los diferentes temas relacionados con la criminalidad, en su estudio afirman que los delitos
… tienen origen en aspectos de los individuos, los cuales dependiendo de las posibilidades que tengan en la sociedad pueden llegar a ser productivos para ésta o pueden tener incentivos a ser criminales y delincuentes dadas las limitaciones que encuentren a progresar personal y laboralmente; así mismo, a partir de las características propias de las zonas geográficas la delincuencia tiende a ser una forma de vida para las personas que aprovechan los recursos que brindan las regiones, lo cual puede llegar a propagarse hacia las zonas aledañas y convertirse en aros de criminalidad que a su vez pueden generar violencia producto del aprovechamiento que desean tener las redes delincuenciales de los dividendos generados por las actividades ilícitas.
Si bien la conducta delictiva puede asociarse a aspectos individuales como la capacidad de autocontrol (Gottfredson y Hirschi, 1990), el consumo de drogas y alcohol (Baron, 2003; Eisner, 2002; Harrison, 1992), traumas en la infancia asociados a violencia intrafamiliar, abuso sexual (Chen, Thrane, Whitbeck, Johnson y Hoyt, 2007), entre otros, tanto como a aspectos sociales del entorno en el cual las personas viven, es razonable pensar que distintos tipos de delitos se asocian a distintos tipos de factores que pueden promover la conducta criminal. Los delitos violentos podrían estar relacionados con aspectos emocionales, como una conducta insegura que lleve a celos -en el caso del feminicidio o la violencia de género-, o sociales, como una idiosincrasia machista o intolerante (Chávez, 2018), aunque en el caso del sicariato el móvil es la búsqueda de lucro por parte del autor material.
Por su parte, en los delitos contra la propiedad es de esperar que la principal motivación del delincuente sea obtener una recompensa monetaria por su actuar con el objetivo de satisfacer sus necesidades económicas. Diferentes estudios realizados mediante métodos estadísticos de tipo espacial, no espacial y temporal han sido realizados con la finalidad de entender las relaciones existentes entre los hurtos y aspectos sociales y económicos. Fajnzylber, Lederman y Loayza (2002) han hallado correlaciones positivas entre las tasas de hurtos y variables que indican pobreza y desigualdad (e. g., índice de Gini, índice de calidad de vida, entre otros) al analizar los datos de 37 países; este mismo estudio evidenció que existen relaciones inversas entre variables relacionadas con el desarrollo económico (e. g., porcentaje de variación del PIB en términos reales). Además, se encontró que el nivel de ingresos promedio, el nivel educativo promedio de la población adulta y el grado de urbanización del país no presentan relaciones significativas con este delito.
Otro indicador de calidad de vida es el índice de necesidades básicas insatisfechas (NBI), el cual ha sido utilizado para identificar y caracterizar la población según las carencias críticas (Mancero y Feres, 2001); por lo tanto, se considera un indicador útil para estimar las condiciones de vida de las personas en la sociedad y por ende se presume que en una población con alto NBI los individuos sean más propensos a cometer hurto en el afán de mejorar sus condiciones de vida. A su vez, el presupuesto destinado a los municipios por parte del Sistema General de Participaciones puede ser una variable relacionada con el número de robos por cuanto se supone que a mayor sea el presupuesto del municipio, mejor será la calidad de vida de las personas y por ende menos estarán motivadas a la delincuencia. Este mismo efecto atenuante se espera de variables como la cantidad de personas con acceso a la educación.
Regresión lineal múltiple
En Charlton y Fotheringham (2009) la regresión es descrita como un conjunto amplio de métodos para modelar las relaciones entre una variable dependiente (Y) y un conjunto de variables independientes (X). En la forma más sencilla, un modelo de regresión lineal múltiple poblacional puede expresarse de la siguiente forma:
En la ecuación anterior
 son las variables respuesta e independientes (predictoras), respectivamente, medidas en la localidad i; 𝜀 𝑖 representa el error aleatorio;
son las variables respuesta e independientes (predictoras), respectivamente, medidas en la localidad i; 𝜀 𝑖 representa el error aleatorio;
 son los coeficientes estimados por el método de Mínimos Cuadrados Ordinarios (MCO) para las 𝑚 variables de forma que se minimice el valor de
son los coeficientes estimados por el método de Mínimos Cuadrados Ordinarios (MCO) para las 𝑚 variables de forma que se minimice el valor de
 en las 𝑛 observaciones.
en las 𝑛 observaciones.
 es el valor predicho por el modelo para la
es el valor predicho por el modelo para la
 observación dado el
observación dado el
 valor de X.
valor de X.
Las predicciones son obtenidas mediante una combinación lineal de las variables independientes. El término
 es denominado residual para la
es denominado residual para la
 observación. Para que el modelo sea válido estadísticamente se debe garantizar que los residuales no presenten autocorrelación serial, se distribuyan de manera normal con media cero y varianza constante, la no existencia de multicolinealidad entre las variables predictoras y que cambios en las variables predictoras tengan efecto en las predicciones, es decir, los parámetros del modelo 𝛽 deben ser significativamente diferentes de cero (Charlton, Fotheringham y Brunsdon, 2006).
observación. Para que el modelo sea válido estadísticamente se debe garantizar que los residuales no presenten autocorrelación serial, se distribuyan de manera normal con media cero y varianza constante, la no existencia de multicolinealidad entre las variables predictoras y que cambios en las variables predictoras tengan efecto en las predicciones, es decir, los parámetros del modelo 𝛽 deben ser significativamente diferentes de cero (Charlton, Fotheringham y Brunsdon, 2006).
Según Brunsdon et al. (1996), el estimador MCO se expresa como
Siendo
 el vector de los coeficientes estimados, X es la matriz de diseño, la cual contiene los valores de las variables independientes y una columna con valores 1; 𝑦 es el vector de los valores observados y
el vector de los coeficientes estimados, X es la matriz de diseño, la cual contiene los valores de las variables independientes y una columna con valores 1; 𝑦 es el vector de los valores observados y
 es la inversa de la matriz de varianza-covarianza (Charlton et al., 2006).
es la inversa de la matriz de varianza-covarianza (Charlton et al., 2006).
Para evaluar la autocorrelación de los residuales se utilizó la prueba de Durbin-Watson (1950, 1951, 1971), que tiene como hipótesis nula la ausencia de autocorrelación.
En los modelos de regresión lineal múltiple se asume que las relaciones entre las variables son las mismas en la zona de estudio, es decir, hay homogeneidad espacial. Sin embargo, dicha suposición puede no cumplirse ya que los procesos que generan los datos pueden variar con el espacio -heterogeneidad espacial (Charlton y Fotheringham, 2009)-. Estas relaciones pueden ser el resultado de diferencias intrínsecas en el espacio debido a diferencias culturales o a contextos políticos distintos (Charlton et al., 2006).
Cuando la regresión lineal es utilizada con datos espaciales, la localización en la que fueron tomados los datos no se tiene en cuenta en el proceso de modelado (Brunsdon, Fotheringham y Charlton, 1998) ya que se asume que el proceso examinado es constante en el espacio y por lo tanto se utiliza un solo modelo (Charlton et al., 2006).
Regresión geográficamente ponderada
La ley de la geografía indica que “Todo se relaciona con todo, pero las cosas cercanas se relacionan más que las lejanas” (Tobler, 1970, p. 236), lo que implica que en procesos espaciales puede no cumplirse la suposición de independencia entre las observaciones asumidas en los modelos de regresión tradicional. Esto es conocido como correlación espacial y puede estar presente en diferentes fenómenos e influir en las estimaciones de los parámetros en un modelo de regresión lineal tradicional ya que, si los residuales del modelo tienen una estructura espacial, la estimación de los parámetros será ineficiente, por lo cual los errores estándar de los parámetros serán muy grandes, produciendo que parámetros potencialmente significativos parezcan no serlo (Gutiérrez-Puebla, García-Palomares y Daniel-Cardozo, 2012).
La regresión geográficamente ponderada fue desarrollada por Brunsdon et al. (1996) como un método para explorar la no estacionariedad espacial, es decir, la condición en la cual un modelo “global” no puede explicar adecuadamente las relaciones entre los conjuntos de variables. Esta situación puede darse en modelos con información georreferenciada en los cuales los coeficientes de la regresión varían con el espacio.
La GWR extiende el método de regresión tradicional, permitiendo estimar parámetros locales en vez de globales (Charlton et al., 2006). De este modo, el modelo puede ser expresado con la siguiente ecuación:
Donde/ denota las coordenadas del 𝑖−é𝑠𝑖𝑚𝑜 punto en el espacio y
 son los coeficientes en el punto 𝑖 (Brunsdon et al., 1996). Por lo tanto, se permite que exista una superficie continua de valores de parámetros, y las mediciones de esta superficie se toman en ciertos puntos para indicar la variabilidad espacial de la superficie (Charlton et al., 2006). De este modo, el modelo de regresión lineal múltiple es un caso particular de la GWR cuando se asume que los parámetros son constantes.
son los coeficientes en el punto 𝑖 (Brunsdon et al., 1996). Por lo tanto, se permite que exista una superficie continua de valores de parámetros, y las mediciones de esta superficie se toman en ciertos puntos para indicar la variabilidad espacial de la superficie (Charlton et al., 2006). De este modo, el modelo de regresión lineal múltiple es un caso particular de la GWR cuando se asume que los parámetros son constantes.
En la GWR los valores próximos al punto 𝑖 son ponderados de acuerdo con su proximidad, es decir, los más próximos influyen más que los lejanos. Algebraicamente, el estimador se puede expresar como
Donde
 es una matriz / compuesta por ceros a excepción de los elementos en la diagonal principal, los cuales representan las ponderaciones geográficas de los datos observados en el punto 𝑖 (Charlton et al., 2006).
es una matriz / compuesta por ceros a excepción de los elementos en la diagonal principal, los cuales representan las ponderaciones geográficas de los datos observados en el punto 𝑖 (Charlton et al., 2006).
Donde
 corresponde al peso del dato en el punto 𝑛 en la calibración del modelo alrededor del punto 𝑖. Las ponderaciones cambian con 𝑖, lo cual establece la diferencia con respecto a la técnica de mínimos cuadrados ponderados, donde la matriz de ponderación es constante (Charlton et al., 2006).
corresponde al peso del dato en el punto 𝑛 en la calibración del modelo alrededor del punto 𝑖. Las ponderaciones cambian con 𝑖, lo cual establece la diferencia con respecto a la técnica de mínimos cuadrados ponderados, donde la matriz de ponderación es constante (Charlton et al., 2006).
En el caso de un modelo de regresión tradicional OLS (i. e. global), la matriz de ponderaciones está implícitamente definida como
lo cual quiere decir que cada dato tiene un peso equivalente a 1, que se interpreta como que no hay variaciones espaciales en los parámetros estimados.
Con la técnica GWR no solo se obtienen coeficientes locales, también se obtienen versiones locales de los diagnósticos utilizados en la regresión tradicional como la bondad de ajuste (R2).
Para evaluar la presencia de autocorrelación espacial de datos medidos en áreas teniendo en cuenta la localización y su valor, se utiliza comúnmente el Estadístico I de Moran (1950) definido como (Environmental Systems Research Institute [ESRI], 2016):
Donde
 son las desviaciones del valor en la posición 𝑖 y en la posición 𝑗, respectivamente, con respecto al valor de la media
son las desviaciones del valor en la posición 𝑖 y en la posición 𝑗, respectivamente, con respecto al valor de la media
 es la matriz de vecindad, la cual define si las posiciones 𝑖,𝑗 son vecinas
es la matriz de vecindad, la cual define si las posiciones 𝑖,𝑗 son vecinas
 o no
o no
 , 𝑛 es el número total de datos.
, 𝑛 es el número total de datos.
Si los datos tienden a un cluster espacial, el índice de Morán será positivo; por el contrario, si los valores altos tienden a estar cerca de valores bajos, el índice será negativo. Además, si los productos positivos entre las desviaciones igualan a los negativos, el índice tenderá a cero. Por lo tanto, el índice de Morán tendrá valores comprendidos entre -1 y 1. Un valor positivo del índice -I de Morán- indica una tendencia hacia la acumulación, mientras que un valor negativo indica una tendencia hacia la dispersión (ESRI, 2016).
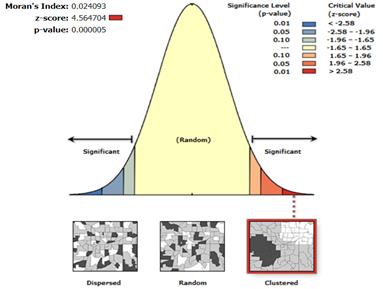
El I de Morán también viene acompañado de un Z-Score y un p-valor que responde a la hipótesis nula de aleatoriedad en los datos, según su resultado se puede concluir lo expresado en la Tabla 1.
Antecedentes
La formulación del modelo GWR ha sido ampliamente utilizada en investigaciones relacionadas con variables georreferenciadas, donde pueden existir cambios considerables en el comportamiento en los coeficientes de las variables analizadas en la región de estudio, como salubridad pública (Fotheringham, Charlton y Brunsdon, 1998; Wheeler y Tiefelsdorf, 2005), mercado inmobiliario (Brunsdon, Fotheringham y Charlton, 1999), en exploración geoquímica (Zhao, Wang y Cheng, 2014), en estudios de movilidad (Gutiérrez-Puebla et al., 2012), en estudios del rendimiento académico (Fotheringham, Charlton y Brunsdon, 2001), estudios biológico-ecológicos (Ortiz-Yusty, Páez y Zapata, 2013), entre otros.
Así mismo, se han realizado estudios que evalúan la relación entre el hurto a motocicletas y factores geográficos en el Valle del Cauca, Colombia, mediante técnicas de econometría espacial, los cuales demuestran que este delito presenta una distribución regional no aleatoria en el espacio (Ramírez, López, Castro y Ocampo, 2017).
Los aspectos relacionados con la criminalidad también han sido analizados mediante el uso de la GWR, tal es el caso del estudio del efecto del terrorismo en el crecimiento económico de Turquía (Öcal y Yildirim, 2010) y el estudio de los crímenes violentos en la ciudad de Portland, Estados Unidos, realizado por Cahill y Mulligan (2007), que reportan la utilidad de la técnica para modelar aspectos sociales como el crimen y reconocen un mejor ajuste en comparación con los modelos de regresión lineal. Así mismo, Rincón-Ruiz, Pascual y Flantua (2013) analizaron los factores asociados con los cultivos de coca y comprobaron que dichas relaciones varían espacialmente. Fowler (2013) analizó algunas variables socioeconómicas y su relación con las tasas municipales de homicidios en Colombia durante el año 2005. Finalmente, Norza et al. (2017) analizaron y compararon en un estudio descriptivo el comportamiento de los principales delitos de alto impacto en la sociedad colombiana entre 2015 y 2016. Se registró un aumento en el número de hurtos a residencias, locales comerciales, motocicletas y a personas, como se observa en la Figura 1.
Metodología
Este estudio es de tipo cuantitativo-correlacional (Dankhe, 1986) en el que se hace uso de información secundaria emitida por diferentes instituciones de orden nacional segregada por municipios; los datos utilizados (Tabla 2) provienen de bases de datos generadas por entidades gubernamentales, entre las que se encuentran el Departamento Administrativo Nacional de Estadística (DANE), el Departamento Nacional de Planeación (DPN), el Ministerio de Educación Nacional, Migración Colombia y el grupo de información de la Policía Nacional de Colombia. La información fue agrupada a nivel municipal y georreferenciada según el Marco Geoestadístico Nacional del año 2017 suministrado por el DANE.
Tabla 2 Variables evaluadas

Transformación utilizada para cumplir los supuestos de normalidad y homocedasticidad, y hacer que datos medidos en escalas diferentes sean más comparables entre sí.
2 https://www.policia.gov.co/grupo-informaci%C3%B3n-criminalidad/estadistica-delictiva
3 https://sicodis.dnp.gov.co/ReportesSGP/SGP_ReportePorEntidadyFuente.aspx
4 https://www.mineducacion.gov.co/sistemasinfo/Informacion-a-la-mano/212400:Estadisticas
5http://www.contaduria.gov.co/wps/wcm/connect/759e1fc3-bd8b-4d63-a95b-f7c37d509140/CT01+-+Categorizacion+2018+-+DNP.xlsx?MOD=AJPERES&CONVERT_TO=url&CACHEID=759e1fc3-bd8b-4d63-a95b-f7c37d509140
6 http://migracioncolombia.gov.co/index.php/es/?option=com_content&view=article&id=718
7 https://www.datos.gov.co/Educaci-n/ESTADISTICAS-EN-EDUCACION-BASICA-POR-MUNICIPIO/nudc-7mev
8 https://www.datos.gov.co/Educaci-n/ESTADISTICAS-EN-EDUCACION-BASICA-POR-MUNICIPIO/nudc-7mev
*La variable categoría corresponde a la clasificación otorgada por la Contaduría General de la República teniendo en cuenta la normatividad vigente definida por el artículo primero de la Ley 617 de 2000 y el artículo séptimo de la Ley 1551 de 2012.
La categorización de los municipios se realiza bajo los siguientes parámetros: los límites definidos de población en ingresos corrientes de libre destinación (en adelante ICLD) y el valor máximo definido de los gastos de funcionamiento como proporción a los ICLD para las diferentes entidades territoriales, importancia económica y situación geográfica según lo estipulado en la Tabla 3.
Tabla 3 Criterios para categorizar a los municipios según el artículo séptimo de la Ley 1551 de 2012

* Salarios mínimos legales mensuales vigentes. Fuente: Contaduría General de la República.
En primer lugar, se realizó un análisis exploratorio de los datos, a partir de la evaluación de la correlación entre las variables, con el objetivo de identificar la posible presencia de relaciones lineales entre la variable predicha y las predictoras, al igual que la posible multicolinealidad entre predictoras. Se modelaron además diferentes regresiones lineales múltiples combinando las distintas variables mediante la función step de la librería stats del programa R (R Core Team, 2018). Adicionalmente, se utilizó un proceso empírico de prueba y error, con el cual se definió el modelo de regresión lineal múltiple que satisface los supuestos de normalidad, homocedasticidad y no multicolinealidad entre variables predictoras. Para complementar, se identificaron los valores atípicos en los residuales del modelo final y se comprobó que corresponden a información real característica de los municipios, por lo cual no fueron eliminados. Es importante mencionar que los modelos fueron elaborados con los datos de 532 municipios, los cuales contaban con la información completa en todas las variables.
Para satisfacer la condición de normalidad y homocedasticidad, las variables fueron recalculadas tomando en cuenta la población total de cada municipio (𝑖) mediante la ecuación (6), con el propósito de obtener una tasa que facilite la comparación entre municipios.
Adicionalmente, se estandarizaron las variables usadas en los modelos mediante la ecuación (7).
Se aplicó una transformación logarítmica a los datos con la intención de mitigar el sesgo a la derecha presente en las variables. Esta transformación permite acotar el rango de las variables y reduce la sensibilidad de las estimaciones a los valores extremos, característica que resulta útil para comparar datos absolutos en inversión, crímenes, población, número de delitos y número de extranjeros en ciudades capitales contra pequeñas poblaciones. De la misma forma, esta transformación permitió que los modelos lineales cumplieran con los supuestos requeridos.
Para la construcción del modelo GWR se utilizó el programa estadístico de uso libre GWR4 (Nakaya, 2016), que permite la manipulación, procesamiento de datos georreferenciados y la aplicación de pruebas estadísticas, entre las que están la prueba de variación geográfica que determina la presencia de cambios significativos de los coeficientes en el espacio. Este modelo fue construido mediante un Kernel tipo “adaptativo bi square” que utiliza la siguiente ecuación para establecer las ponderaciones:
Los modelos fueron validados mediante varias pruebas: el de Shapiro-Wilk (Shapiro y Wilk, 1965) para evaluar la normalidad en los residuos, el de Breusch-Pagan (Breusch y Pagan, 1979) para garantizar la igualdad de varianza, el test de Durbin-Watson (1950, 1951, 1971) que tiene como hipótesis nula la ausencia de autocorrelación y el criterio de Factor de Inflación de Varianza (VIF1) para identificar la posible existencia de multicolinealidad entre variables regresoras.
Una vez obtenidos los modelos finales (GWR y regresión lineal múltiple), se visualizaron geográficamente los residuales en ArcMap y se calculó el I de Morán (Moran, 1950) para determinar la presencia de correlación espacial. Finalmente, la comparación entre modelos se realizó mediante los criterios de información de Akaike, Bayesiano y el coeficiente de determinación ajustado (Ra 2).
Resultados
Análisis exploratorio de los datos
Mediante un análisis de los coeficientes de correlación de Pearson, entre las diferentes variables estudiadas se logró determinar las asociadas al hurto, proceso que permitió descartar algunas variables como predictoras e identificar redundancia de información aportada por algunas variables. En este sentido, la Figura 1 muestra que la única variable altamente correlacionada con el hurto a personas y de celulares es la población total (PobTotal). Las demás variables presentan correlaciones por debajo de 0,5. Tampoco existen correlaciones importantes entre las variables predictoras. La relación entre el presupuesto per cápita asignado en el Sistema General de Participaciones (sgp_percapita) y el hurto, aunque es muy baja, presenta el comportamiento esperado (a mayor presupuesto por persona, menor el número de hurtos).
Figura 2. Matriz de correlación de las variables
* hurto corresponde al número de hurto a personas y celulares en 2017.
** MATRI1000P corresponde al número de matriculados en instituciones superiores por cada 1.000 personas.
*** sgp_percápita corresponde al presupuesto per cápita asignado por el Ministerio de Hacienda.
**** PobRural corresponde a la población rural.
***** PobTotal corresponde a la población total.
****** extran1000p corresponde al número de extranjeros por cada 1.000 personas.
******* COBERTURA_NETA corresponde a la cobertura neta de educación.
En la Figura 3 se observa una disminución del número de hurtos (logaritmo de los hurtos) al aumentar la categoría de los municipios. Es decir, la mayor cantidad de delitos registrados se localiza principalmente en las ciudades capitales, en municipios de categoría especial (categoría cero) y de categoría uno. La mayor dispersión se presenta en los municipios de categoría 6. Es importante resaltar que existen municipios con baja población que presentan alto número de hurtos registrados, como el caso de algunos localizados en la región de los Llanos Orientales (Figura 4).

En este apartado se presentan los resultados para los modelos de regresión lineal múltiple y el espacial (GWR)
Figura 4 Hurto a personas y celulares
Al realizar el análisis descriptivo de la variable hurto, se observa que en promedio se registraron en el 2017 en los 532 municipios 2,1 hurtos por cada mil habitantes, con una desviación estándar de 2,52. El valor mínimo fue de 0,03 en Moñitos, en el departamento de Córdoba, y el máximo, 15,6, en Pasto, departamento de Nariño.
En la Figura 5 se aprecia que existe una dispersión grande en los recursos económicos per cápita asignados por el Sistema General de Participaciones. En promedio, el presupuesto per cápita asignado por el SGP es de 530.090 pesos, con una desviación estándar de ±232.439; el valor mínimo es de 136.461 pesos, asignado al municipio de Sopó, en el departamento de Cundinamarca, y el valor máximo es de 2’059.951 pesos, asignado al municipio de San Miguel, en el departamento de Santander.

En este apartado se presentan los resultados para los modelos de regresión lineal múltiple y el espacial (GWR)
Figura 5 Presupuesto per càpita a partir del Sistema General de Participaciones
La Figura 6 muestra que las principales ciudades del país (Bogotá, Cali, Barranquilla, Medellín, Bucaramanga y Cartagena) concentran el mayor número de estudiantes de educación superior (IES). El valor promedio de matriculados en IES es de 28,1 por cada mil habitantes; sin embargo, al hacer comparables los municipios por medio de la tasa de matriculados por cada mil personas, en el municipio de Marinilla, en el departamento de Antioquia, se presenta la menor tasa, con 0,018 estudiantes por cada mil personas. De forma opuesta, en Nilo, Cundinamarca, y Pamplona, Norte de Santander, más del 51% de sus habitantes se encuentran realizando estudios de educación superior, seguidos por Bucaramanga, Santander, con una proporción de más del 40%.
El número de municipios en cada categoría y su localización se presenta en la Figura 7.
Modelo de regresión lineal múltiple

En este apartado se presentan los resultados para los modelos de regresión lineal múltiple y el espacial (GWR)
Figura 6 Matriculados en instituciones de educación superior
Modelo de regresión lineal múltiple
En la Tabla 4 se presentan los modelos lineales generados con el resultado de los valores AIC, BIC el R a 2 en porcentaje y las pruebas de normalidad, homocedasticidad y multicolinealidad. Nótese que entre los modelos evaluados, solo los “Modelo 14”, “Modelo 15” y “Modelo 16” cumplen con los supuestos de normalidad y homocedasticidad.
Tabla 4 Modelos lineales evaluados y diagnóstico

* Se cumple al 5% de significancia.
** Se cumple al 5% de significancia.
El modelo final (modelo 16) que tiene como grupo de referencia a los municipios con categoría especial se puede expresar de la siguiente manera:
El factor de inflación de varianza del modelo (Tabla 5) indica que no existen relaciones lineales fuertes entre variables predictoras. Por tanto, el modelo no presente multicolinealidad.
Analizando cada una de las variables involucradas en el modelo anterior y manteniendo constantes las variables no mencionadas, se tiene que
Para un aumento del 1% en la tasa de matriculados por cada mil personas, en promedio se espera un aumento del 0,21% en la cantidad de hurtos.
Para un incremento del 1% en la inversión del SGP por habitante, se espera una reducción del 1,3% en promedio en la cantidad de hurtos.
Así mismo, el modelo indica que los municipios clasificados en las categorías uno, dos, tres, cuatro, cinco y seis presentan respectivamente en promedio 1,3%, 2,3%, 3,6%, 3,19%, 4,2% y 5,25% de hurtos menos en comparación con la categoría especial.
De los resultados obtenidos, este modelo (modelo 16 -ecuación 9-) fue escogido por principio de parsimonia entre aquellos que cumplieron con los supuestos de normalidad, ausencia de multicolinealidad e igualdad de varianza y significancia estadística (p-valor < 0,05). Sin embargo, el modelo no cumple con el supuesto de autocorrelación entre los residuos, determinado a partir de test de Durbin Watson y partiendo de ello se aplicará a los datos un test de autocorrelación espacial. En cuanto a los análisis por variable, se confirma la significancia de cada una de ellas. Finalmente, se puede afirmar que el modelo explica 65,9% de la variación del logaritmo del hurto.
Modelo GWR
A partir del resultado del test de autocorrelación de Durbin-Watson aplicado a los residuales del modelo, se evaluó la autocorrelación espacial mediante el índice de Morán, el cual con un valor de 0,091625, y un p-valor < 0,001 apoya concluir que existe agrupamiento espacial en los residuales del modelo.
En el mapa de residuales del modelo lineal (Figura 8) se destacan, con circunferencias negras, los clusters de altos residuales presentes en la región Caribe y en el departamento de Caquetá.
Al comprobarse la existencia de autocorrelación espacial en los residuales del modelo de regresión lineal múltiple final -ecuación 9-, se construyó un modelo GWR utilizando las mismas variables, con excepción de la variable categórica, debido al alto riesgo de presentar problemas de multicolinealidad local producto del alto agrupamiento espacial que exhibe esta variable y de que los modelos GWR se centran en variables que siguen distribuciones gaussianas (Dong, Nakaya y Brunsdon, 2018).
Intercepto del modelo GWR
Los valores más bajos se encuentran agrupados hacia el sur y suroeste del país, en los municipios de Puerto Nariño y Leticia, en el Amazonas, y Puerto Leguízamo, en el Putumayo.
Por otro lado, los valores más altos se concentran en el nororiente del país, en los municipios de Sardinata y Ocaña, en el departamento de Norte de Santander, y San Alberto, en el Cesar (Figura 9).
Coeficiente variable logsgppercapita
En la Figura 10 se observa que el coeficiente de la variable presupuesto per cápita asignado por el Sistema General de Participaciones, transformada logarítmicamente, presenta una correlación negativa con el hurto en todo el país, por lo cual tiene un comportamiento atenuante en relación con el hurto; sin embargo, esta relación es variable espacialmente. Los municipios con mayor valor se concentran hacia el sur y suroeste del país, en Puerto Nariño y Leticia, en el Amazonas, y Puerto Leguízamo, en el Putumayo.
Los valores más bajos se concentran hacia la zona del Magdalena medio: Norte de Santander -Sardinata, Gramalote- y Cesar -San Alberto-. Esto indica que en estas regiones esta variable influye en menor medida sobre los hurtos.
Coeficientes variables logmatri1000p
En la Figura 11 se observa que la tasa de matriculados en instituciones de educación superior por cada mil personas presenta una relación directa con el hurto; sin embargo, esta relación varía espacialmente en menor medida en comparación con la variable logsgppercapita y el intercepto del modelo.
Los valores más altos se concentran en el norte y suroeste del país, siendo los municipios de Tumaco y El Charco, en el departamento de Nariño, y Guapi, en el Cauca, los que presentan los mayores coeficientes.
Por otra parte, los menores valores se concentran principalmente en los departamentos de Antioquia y los Santanderes; los municipios de Amalfi, Yolombó y Yondó, en Antioquia, presentan los menores coeficientes.
Tal como los señalan Estrada y Durán (2015, p. 10), en los procesos espaciales no se cumplen los supuestos de normalidad y homocedasticidad
… debido a lo irregular de las unidades geográficas (los municipios) por diferencias significativas de áreas, y fundamentalmente por el papel del espacio, que no es sólo contenedor de información, sino factor explicativo de los procesos que en él se presentan. Por lo tanto, los procesos espaciales tienden a ser no estacionarios, es decir, que presentan variación regional o local.
El modelo resultante (Figura 13) indica que aproximadamente el 50% de la variabilidad del logaritmo del hurto a personas y celulares es explicado por las variables predictoras.
A partir del modelo GWR se obtienen valores de los coeficientes para las variables en cada municipio. Los resultados mostrados en la Tabla 6 indican que la variable logsgppercapita es la que presenta mayor variación geográfica, con una desviación estándar de 0.2120, lo que podría indicar que diferencias en la inversión per cápita en los 532 municipios incluidos en el modelo inciden en los indicadores de hurto. Por otro lado, la tasa de matriculados por cada mil personas muestra una baja dispersión, con un coeficiente de variación del 12,5%.
Tabla 6 Mínimo, máximo, rango y valor promedio de los estimadores de las variables predictoras del modelo GWR

La prueba de variabilidad geográfica tiene como objetivo evaluar si las variables predictoras presentan variabilidad significativa en su coeficiente Beta a nivel espacial. El resultado mostrado en la Figura 14 indica que existe variación significativa en el intercepto, y en la variable logsgppercapita (logsgpperc), por el contrario, la variable logmatri1000p (logmatri10) no varía significativamente. Esto se deduce a partir del valor DIFF of Criterion (AICc) menor a 2, que es el resultado de la diferencia entre los AICc de los modelos con el parámetro global o local. Lo anterior concuerda con la poca dispersión observada en el coeficiente de la variable logmatri1000p presentado en Tabla 5.

Fuente: Resultados obtenidos a partir del programa GWR4.
Figura 14 Resultado del test de variabilidad espacial.
En la Figura 12 se observa el mapa de distribución de los residuales estandarizados del modelo GWR, los cuales, a partir del resultado del índice de Morán mostrado en la Figura 15, no se encuentran distribuidos aleatoriamente ya que existe agrupamiento espacial. Este comportamiento puede ser debido a la ausencia de variables clave en el modelo.
Finalmente, el coeficiente de determinación R2 del modelo GWR mostrado en la Figura 16 indica que existen diferencias en el ajuste del modelo a nivel espacial. El menor ajuste se observa en el departamento de Córdoba y la región del Urabá, donde las variables predictoras logran explicar tan solo entre 39 y el 43% aproximadamente de la variabilidad del hurto. Por otro lado, el mejor ajuste del modelo GWR se presenta hacia el centro del país en los departamentos de Cundinamarca, Boyacá y el sur de Santander principalmente, donde se alcanzan cifras entre el 53 y 57% de variabilidad explicada.
Comparación entre los modelos de regresión lineal múltiple y el modelo GWR
Para comparar modelos equivalentes, se realizó un modelo de regresión lineal múltiple sin tomar en cuenta la categoría del municipio (MCO global) ya que este con las variables logmari1000p, logsgppercapita no cumple los supuestos de normalidad y homogeneidad de varianza.
Al comparar el modelo OLS global con su equivalente GWR, se observa que el modelo espacial explica en aproximadamente 4% más la variabilidad del hurto a personas y celulares. De igual forma, presenta un menor AIC.
Al cotejar el modelo de regresión lineal múltiple final (OMC Modelo 16), que incluye la variable Categoría, con el resto, se logra un aumento considerable en el R2, una disminución del AIC y un modelo que cumple con los supuestos de normalidad y homocedasticidad en los residuales (Tabla 7).
Conclusiones
El modelo de regresión lineal múltiple estimado por mínimos cuadrados ordinarios que tiene como variables predictoras el presupuesto per cápita asignado por el Sistema General de Participaciones y la tasa de matriculados en instituciones de educación superior por cada mil habitantes requirió una transformación logarítmica y la inclusión de la variable nominal categoría del municipio. De esta forma, se cumple con los supuestos de normalidad y homocedasticidad de los residuales y no multicolinealidad en las variables predictoras. Este modelo logra explicar el 69,5% de la variabilidad del logaritmo de los hurtos a personas y celulares registrados por la Policía Nacional durante el año 2017 en los 532 municipios incluidos en el análisis. Sin embargo, este tipo de modelos realiza una valoración global sin considerar la localización de los datos; por lo tanto, no tiene en cuenta las posibles heterogeneidades propias de los territorios, que se reflejan en la presencia de autocorrelación espacial de los residuales.
El modelo de regresión ponderada geográficamente estimado mediante el uso de un kernel de tipo adaptativo bi-square según el criterio de selección AICc, con las variables predictoras: presupuesto per cápita asignado por el Sistema General de Participaciones y la tasa de matriculados en instituciones de educación superior por cada mil habitantes, ambas transformadas logarítmicamente, sin incluir la variable categoría, explica el 50,16% de la variación del logaritmo del hurto con un AIC de 1955,9. De esta forma, se obtiene un mejor ajuste en comparación con el mismo modelo de regresión lineal múltiple estimado mediante mínimos cuadrados ordinarios, el cual presenta un coeficiente de determinación de 46,1 y un AIC de 1969,8. Por lo tanto, se puede concluir que al aplicar la técnica GWR a datos que presentan autocorrelación espacial, se obtienen mejores resultados.
A pesar del mejor ajuste logrado mediante la técnica GWR en comparación con el mismo modelo estimado por mínimos cuadrados ordinarios, el método de regresión espacial está limitado al uso de variables numéricas. Por tanto, al no permitir el uso de variables categóricas, se restringe el uso de posible información clave para el modelo.
La inclusión de la categoría del municipio en el modelo aumentó el coeficiente de determinación a 69,96%, lo cual representa una mejora de 19,44% con respecto al modelo GWR (que presentó un R2 de 50,16%) y del 23,83% respecto al modelo de regresión múltiple sin la variable categórica.
Del análisis realizado y los modelos evaluados se puede deducir que, para los 532 municipios incluidos en el modelo, las variables cantidad de extranjeros por cada mil habitantes, población rural y cobertura neta en educación preescolar, básica, media y secundaria no presentan relación significativa con el hurto a personas y celulares durante el año 2017.
En los tres modelos finales se observa una relación inversa entre el hurto a personas y celulares y el presupuesto per cápita asignado a través del Sistema General de Participaciones, con lo que se concluye que a mayor inversión en los municipios, sin importar su localización, se tiende a reducir las cifras de hurtos.
Los matriculados en instituciones de educación superior por cada mil habitantes presentan una relación directa con el hurto a personas y celulares, relación que posiblemente sea el reflejo de una tendencia en este tipo de hurtos en zonas de alto flujo de personas, como lo son los centros universitarios. Sin embargo, este resultado amerita estudios posteriores sobre la conducta criminal y ocurrencia de delitos que permitan aclarar el porqué de esta relación.
Los resultados obtenidos indican que cuanto mejor es la categoría de los municipios, mayor es la ocurrencia de hurtos a personas y celulares.
Recomendaciones
Los estudios sobre criminalidad, especialmente los enfocados en atentados contra el patrimonio económico, requieren de la inclusión de variables e información relacionada con la calidad de vida y pobreza, ya que es razonable pensar que este tipo de delitos está motivado por el insuficiente acceso a condiciones de vida dignas asociadas a bajos ingresos. Se recomienda para futuros estudios la inclusión de las variables distintos indicadores de pobreza y tasas de desempleo, que no fueron incluidas en este estudio debido a la ausencia de datos actualizados y segregados a nivel municipal.
Los modelos obtenidos pueden ser utilizados como insumo en posteriores estudios de política pública cuyo objetivo sea mitigar el hurto a nivel municipal teniendo en cuenta la heterogeneidad del territorio.
Para futuros estudios sobre criminalidad, se recomienda tener en cuenta variables disuasivas que dificultan la ejecución de los delitos, como el pie de fuerza policial, militar y judicial presente de los municipios. Esta información no fue tenida en cuenta en este estudio debido a la falta de información de fácil acceso público.
La regresión geográfica permite mejorar los ajustes, neutralizar la dependencia espacial en los residuos y conocer la distribución espacial tanto de las elasticidades en las variables explicativas como en la significación local del modelo, todo ello sin renunciar al carácter directo y de respuesta rápida (Gutiérrez-Puebla et al., 2012, p. 1). Además, la combinación de precisión, bajo coste y sencillez hace que los modelos estadísticos se conviertan en una alternativa razonable para municipios de tamaño pequeño o de recursos limitados que necesitan evaluar de forma rápida y precisa el número de hurtos.