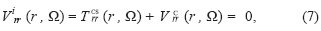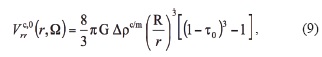Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Earth Sciences Research Journal
Print version ISSN 1794-6190
Earth Sci. Res. J. vol.19 no.2 Bogotá July/Dec. 2015
http://dx.doi.org/10.15446/esrj.v19n2.44574.
GRAVITY
Isostatic Crustal Thickness Under The Tibetan Plateau And Himalayas From Satellite Gravity Gradiometry Data
Espesor isostático de la corteza bajo la meseta tibetana y los Himalayas a partir de datos satelitales de gradiente gravitatoria
Robert Tenzer1, Mohammad Bagherbandi2, Lars E Sjöberg2, Pavel Novák3
1 Wuhan University, China, Hubei, China
2 Royal Institute of Technology, Sweden, Estocolmo, Suecia
3 University of West Bohemia, Czech Republic, Plzeň, República Checa
Record
Manuscript received: 23/07/2014 Accepted for publication: 27/07/2015
How to cite item
Tenzer, R., Bagherbandi, M., Sjöberg, L.E. & Novák, P. (2015). Isostatic crustal thickness under the Tibetan Plateau and Himalayas from satellite gravity gradiometry data. Earth Sciences Research Journal, 19(2), 97-106. http://dx.doi.org/10.15446/esrj.v19n2.44574.
ABSTRACT
The global gravity and crustal models are used in this study to determine the regional Moho model. For this purpose, we solve the Vening Meinesz-Moritz's (VMM) inverse problem of isostasy defined in terms of the isostatic gravity gradient. The functional relation between the Moho depth and the second-order radial derivative of the VMM isostatic potential is formulated by means of the (linearized) Fredholm integral equation of the first kind. Methods for a spherical harmonic analysis and synthesis of the gravity field and crustal structure models are applied to evaluate the gravity gradient corrections and the respective corrected gravity gradient, taking into consideration major known density structures within the Earth's crust (while mantle heterogeneities are disregarded). The resulting gravity gradient is compensated isostatically based on applying the VMM scheme. The VMM inverse problem for finding the Moho depths is solved iteratively. The regularization is applied to stabilize the ill-posed solution. The global geopotential model GOCO-03s, the global topographic/bathymetric model DTM2006.0 and the global crustal model CRUST1.0 are used to generate the VMM isostatic gravity gradient with a spectral resolution complete to a spherical harmonic degree of 250. The VMM inverse scheme is used to determine the regional isostatic crustal thickness beneath the Tibetan Plateau and Himalayas (compiled on a 1x1 arc-deg grid). The differences between the isostatic and seismic Moho models are modeled and subsequently corrected for by applying the non-isostatic correction. Our results show that the regional gravity gradient inversion can model realistically the relative Moho geometry, while the solution contains a systematic bias. We explain this bias by more localized information on the Earth's inner structure in the gravity gradient field compared to the potential or gravity fields.
Keywords: Density, gravity gradiometry, isostasy, Moho interface.
RESUMEN
Este estudio utiliza los modelos globales de gravedad y de espesor de la corteza para determinar un modelo regional de la discontinuidad de Mohorovičić (Moho). Con este fin se resolvió el problema inverso de isostasia Vening Meinesz-Moritz (VMM) definido en términos de gradiente gravitatoria isostática. La relación funcional entre la profundidad de la Moho y la derivación radial de segundo orden del potencial isostático VMM fue formulado a través de la ecuación integral Fredholm de primera clase. Se aplicaron métodos para el análisis esférico armónico y para la síntesis del campo gravitacional, y los modelos de estructura de corteza para evaluar las correcciones de gradiente gravitatoria y el respectivo gradiente gravitatorio corregido, considerando el conocimiento de las principales densidades de la estructura al interior de la corteza de la Tierra (las heterogenidades del manto fueron ignoradas). El gradiente gravitatorio resultante se compensó isostáticamente con la aplicación del esquema VVM. Se resolvió reiterativamente el problema inverso VVM para encontrar las profundidades de la discontinuidad Moho. Se aplicó la regularización para estabilizar la solución planteada. El modelo geopotencial global GOCO-03s, el modelo global topográfico/batimetrico DTM2006.0 y el modelo global de la corteza CRUST 1.0 permitieron generar el gradiente gravitacional isostático VVM con una resolución espectral completa a un grado esférico armonioso de 250. A través del esquema inverso VMM se determinó el espesor isostático regional bajo la meseta Tibetana y los Himalayas (compilada en una cuadrícula de 1x1 grados sexagesimales). Las diferencias entre los modelos isostático y sísmico de la Moho fueron modeladas y corregidas con la aplicación de la corrección no isostática. Los resultados muestran que la inversión del gradiente gravitatorio puede modelar realísticamente la geometría de la Moho, a pesar que la solución contiene una desviación sistemática. Esta inclinación se explica por la información estructural interna de la Tierra en el campo del gradiente gravitatorio comparado con el potencial gravitatorio.
Palabras clave: Densidad, gradiometria gravitatoria, isostasia, discontinuidad de Mohorovičić.
INTRODUCTION
Gravimetric methods for the Moho depth determination have been developed and applied in global and regional studies. Examples of the gravimetric methods include, but are not limited to, studies by Čadek and Martinec (1991), Braitenberg and Zadro (1999), Braitenberg et al. (2000a, 2000b, 2006), Arabelos et al. (2007), and Sjöberg (2009). Gravimetric methods should optimally combine the gravity and seismic data (if available). Braitenberg and Zadro (1999) proposed a method based on the iterative 3-D gravity inversion with integrated seismic data. Sjöberg and Bagherbandi (2011) developed and applied a least-squares approach based on solving the Vening Meinesz-Moritz (VMM) inverse problem of isostasy (Sjöberg 2009). This gravimetric method used the constraining information from the seismic model. They also presented a method of modeling the differences between isostatic and seismic models by applying the non-isostatic correction (Bagherbandi and Sjöberg 2012).
The gravimetric determination of the Moho depth has been typically realized using the isostatic gravity (or potential) field quantities. Sampietro (2011) discussed possibilities of using the gravity gradiometry data provided by the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE). Bagherbandi (2011) developed an iterative method to recover the Moho geometry using directly the GOCE gravity gradiometry data. His formulation of the isostatic scheme for the gravity gradient field was based on solving the VMM problem of isostasy. Bagherbandi and Eshagh (2012) applied this theory to the real gradiometry data of GOCE. Their simulation study revealed a relatively good agreement between their global solution and the CRUST2.0 Moho seismic model (Bassin et al. 2000); the RMS of differences was found to be ῀5 km. Reguzzoni and Sampietro (2012) presented a case study to assess the inversion algorithm based on the linearization of Newton's gravitational law by exploiting the GOCE observables. They proposed a possible solution using the (local) Fourier analysis and the Wiener deconvolution of satellite data. Sampietro et al. (2013) presented the GOCE estimated Moho depths beneath the Tibetan Plateau and Himalayas. They showed that the expected Moho geometry has a good agreement with existing local seismic profiles. The GOCE-only solution was improved by using seismic profiles as additional observations; the RMS of residuals with respect to the seismic profiles was found to be ∼4 km. Eshagh (2014) developed a linear approach to determine the Moho geometry from satellite gradiometry data and investigated some numerical aspects of the gravity gradiometry inversion.
In the studies mentioned above, the Moho determination was realized using only the gravity gradiometry data (Bagherbandi and Eshagh 2012, Eshagh 2014). Sampietro et al. (2013) used the seismic data to improve the gravimetric Moho solution. In this study, we incorporate the information from seismic data directly to the VMM gravimetric solution for finding the Moho depths. This is done by combing the gravity and seismic crustal structure models in computing the isostatic gravity gradient and solving the VMM inverse problem of isostasy. For this purpose, we combine three recently developed numerical methods for a regional determination of the Moho geometry from the isostatic gravity gradient. The computation of the gravity gradient is realized according to the approach introduced by Tenzer et al. (2012a). They presented a uniform mathematical formalism of computing the gravity corrections and respective corrected gravity field. Novák and Tenzer (2013) applied this method to evaluate the diagonal elements of the (second-order) Marussi gravity gradient tensor corrected for major known anomalous density structures within the Earth's crust. We further apply the VMM scheme to evaluate the isostatic gravity gradient and to estimate the isostatic Moho model according to the procedure of Bagherbandi (2011). Regarding to Bagherbandi and Sjöberg (2012), we finally define and apply the non-isostatic gravity gradient correction for combining the isostatic and seismic models. The VMM isostatic model and its gravity gradient modification are briefly recapitulated in Sections 2 and 3. The non-isostatic gravity gradient correction is defined in Section 3. The numerical experiment is conducted in the study area covering the Tibetan Plateau and the Himalayas (characterized by the largest continental crustal thickness). Summary of published seismic and gravimetric studies of the Moho geometry at the study area can be found in Tenzer et al. (2013). Results are presented and discussed in Section 5. The summary and concluding remarks are given in Section 6.
Vening Meinesz-Moritz problem of isostasy
Sjöberg (2009, 2013) formulated the VMM problem of isostasy in the following generic form
where G = 6.674 × 10 -¹¹ m3 kg-1 s-2 is the Newton's gravitational constant, R= 6371 × 103 m is the Earth's mean radius, ∆ρc/m is the Moho density contrast (in kg/m3), and f is the isostatic gravity functional. The 3-D position is defined in the spherical coordinate system (r,Ω) ; where r is the spherical radius, and Ω = (ø,λ) is the spherical direction with the spherical latitude ø and longitude λ . The infinitesimal surface element on the unit sphere is denoted as: d Ω' = cosø' dø;' dλ', and Φ {Ω' = (ø', λ'): ø' ∈ [-π/2, π/2] ∧λ' ∈ [0,2 π)} is the full spatial angle. The integral kernel K in Eq. (1) is a function of the spherical distance ψ and the Moho-depth parameter s= 1-τ , with D'/ R and D' is the Moho depth. The spectral representation of K reads (cf. Sjöberg 2009)
where Pn is the Legendre polynomial of degree n for the argument of t = cosψ.
The integral equation in Eq. (1) functionally relates the (unknown) Moho depths with the (given) isostatic gravity data (i.e., the isostatic gravity disturbances or anomalies). For the isostatic gravity disturbance δg-i, the isostatic gravity functional f on the right-hand side of Eq. (1) becomes (cf. Tenzer and Bagherbandi 2012)
where g-c is the isostatic compensation attraction (Moritz 1990, Sjöberg 2009), and δg-cs is the consolidated crust-stripped gravity disturbance (Tenzer et al. 2009). The evaluation of δg-cs from the gravity disturbance δg is based on applying the topographic and stripping gravity corrections due to major known anomalous crustal density structures. These refined gravity data should have (theoretically) a maximum correlation with the Moho geometry (Tenzer et al. 2012b). However, these gravity data still comprise the long-wavelength gravity signal of unmodelled heterogeneities within the lithospheric mantle and the asthenosphere (including the core-mantle boundary zone) as well as uncertainties within the crustal model. The isostatic compensation attraction g-c in Eq. (3) is given by (cf. Sjöberg 2009)
where D0 is the nominal (mean) value of the Moho depth, ℓ is the Euclidean spatial distance of two points (r, Ω) and (r', Ω'), and ψ is the respective spherical distance. The formula in Eq. (3) defines the condition of the VMM isostatic equilibrium by means of a fully-compensated crustal model.
The expression in Eq. (1) is a (non-linear) Fredholm integral equation of the first kind. Its direct solution was given by Sjöberg (2009) in the form of a second-order approximation
The term D1 is computed approximately using the following spectral expansion
where Yn,m are the (fully-normalized) surface spherical harmonics of degree 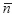 and order m, fn,m are the numerical coefficients of the functional f, and n is the maximum degree of spherical harmonics. The third constituent on the right-hand side of Eq. (5) has a singularity for ψ →0 . Sjöberg (2009) solved this integral singularity by applying a planar approximation to the inner-zone contribution. This constituent is computed by implementing the surface integration over the inner zone (while disregarding the distant-zone contribution). The system of integral equations for finding the Moho depths is then solved directly without applying an iterative procedure.
and order m, fn,m are the numerical coefficients of the functional f, and n is the maximum degree of spherical harmonics. The third constituent on the right-hand side of Eq. (5) has a singularity for ψ →0 . Sjöberg (2009) solved this integral singularity by applying a planar approximation to the inner-zone contribution. This constituent is computed by implementing the surface integration over the inner zone (while disregarding the distant-zone contribution). The system of integral equations for finding the Moho depths is then solved directly without applying an iterative procedure.
Vening Meinesz-Moritz isostatic model for the gravity gradient
Bagherbandi (2011) reformulated the VMM inverse problem of isostasy for the second-order radial derivative of the isostatic potential V i; i.e., V irr = ∂2V i/∂r2. By analogy with Eq. (3), he established the isostatic condition for the component V irr as follows (see also Bagherbandi and Eshagh 2012)
where the second-order radial derivatives of the consolidated crust-stripped disturbing potential TCS and the isostatic compensation potential V c are denoted as TCSrr and V Crr, respectively. The computation of the consolidated crust-stripped gravity gradient TCSrr is summarized in Appendices A and B. Bagherbandi (2011) applied a decomposition of the isostatic compensation gradient V c into the nominal and residual parts:
The nominal part Vc,orr is computed from the following formula
where τ0 = D0 / R. With reference to Eq. (1), the residual part dV crr is given by
where the integral kernel function  rr reads
rr reads
Bagherbandi (2011) derived the solution to the integral equation in Eq. (10) in the following form
where ds = 1- dτ is a function of the differential Moho-depth correction (i.e., dτ = dD'/R ), and the isostatic gravity gradient functional f is defined as
The Moho-depth corrections dD' are found based on solving the VMM inverse problem of isostasy formed for the given values of the isostatic gravity gradient. The final Moho depths D' are obtained by adding these corrections dD' to the nominal Moho depth D0 ;i.e.,D'= D0+dD'.
From Eq. (11), the partial derivative of the kernel function  rr with respect to the argument s was found to be
rr with respect to the argument s was found to be
The corresponding closed analytical form of Eq. (14) was given by Bagherbandi (2011). The linearization of  rr by means of the Taylor series yields
rr by means of the Taylor series yields
where s1 is an approximate value to the argument s.
Non-isostatic correction
The isostatic mass balance depends on loading and effective elastic thickness, rigidity, rheology of the lithosphere and viscosity of the asthenosphere (e.g., Watts 2001). Moreover, the glacial isostatic adjustment, present-day glacial melting, plate motion, mantle convection and other geodynamic processes contribute to the overall isostatic balance, which are not modeled realistically by the adopted isostatic model. It imply that: δgi ≠ 0. To fulfill the condition of the isostatic equilibrium of f = δgi = 0 in Eq. (3), Bagherbandi and Sjöberg (2012) introduced the non-isostatic correction term. By analogy with their definition, we apply the non-isostatic correction V nierr to the isostatic gravity gradient functional f in Eq. (13). Hence
The non-isostatic gravity gradient correction V nierr is given by
The coefficients Cnien,m are generated by applying the following integral convolution
The non-isostatic gravitational attraction gnie is computed approximately from (cf. Sjöberg 2009)
where  is the seismic Moho depth, and the nominal compensation attraction (of zero-degree)
is the seismic Moho depth, and the nominal compensation attraction (of zero-degree)  stipulated at the sphere of radius R is computed as
stipulated at the sphere of radius R is computed as
Results
The study area of the Tibetan Plateau and Himalayas is bounded by the parallels of 25 and 40 arc-deg northern latitudes and the meridians of 70 and 110 arc-deg eastern longitudes. The solid topography of the study area is shown in Fig. 1. The solid topography was computed on a 1×1 arc-deg grid using the coefficients of the DTM2006.0 global topographic/bathymetric model (Pavlis et al. 2007) with a spectral resolution complete to degree/order 250. The maximum bathymetric depth is 0.3 km, and the maximum topographic heights reach 5.8 km.
1. Isostatic gravity gradients
We applied the gravimetric forward modeling technique to compute the VMM isostatic gravity gradient with a spectral resolution complete to degree 250 of spherical harmonics. All gravity gradient-related computations were realized on a 1×1 arc-deg surface grid. The computation consists of three numerical steps. The spherical harmonic analysis of the crustal density structures (Eqs. A.4-A7) was first applied to generate the coefficients Ln,m and Un,m , which describe the mass density (or the density contrast) distribution within the topography, seawater (bathymetry), sediments and remaining crustal structures. The spherical harmonic synthesis (Eqs. A.1-A.3 and Eqs. B.1-B3) was then applied to compile the respective gravity gradient corrections and the consolidated crust-stripped gravity gradient. The ice stripping correction due to glacial cover of the Tibetan Plateau and Himalayas was not applied due to the absence of reliable data of the ice thickness. The VMM isostatic gravity gradient was finally obtained from the consolidated crust-stripped gravity gradient after applying the isostatic compensation gradient (see Section 3).
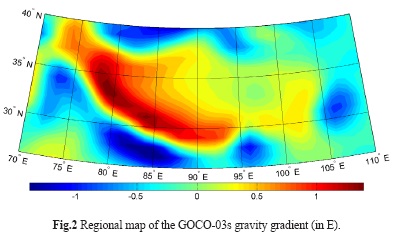
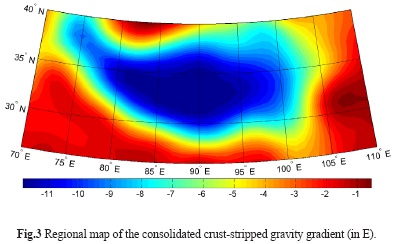
The gravity gradient was generated using the GOCO-03s coefficients (Mayer-Guerr et al. 2012). The parameters of GRS-80 (Moritz 2000) were used to define normal gravity gradient. The topographic and bathymetric stripping gravity gradient corrections were calculated using the DTM2006.0 coefficients (Pavlis et al. 2007). The average density of the upper continental crust of 2670 kg m-3 (see Hinze 2003) was adopted as the topographic density. The same value was used to define the reference crustal density. The bathymetric stripping gravity gradient correction was evaluated utilizing the seawater density-depth equation (Tenzer et al. 2011). The 1×1 arc-deg data of sediments and consolidated crustal layers from the global crustal model CRUST1.0 were used to evaluate the respective stripping gravity gradient corrections. Note that these two corrections we computed with a spectral resolution only up to degree 180 of spherical harmonics.
The GOCO-03s gravity gradient over the study area is shown in Fig. 2. It ranges from -1.4 to 1.4 E (E = Eötvös), with a mean of -0.04 E and a standard deviation of 0.6 E. The regional map of the consolidated crust-stripped gravity gradient is shown in Fig. 3. This refined gravity gradient is everywhere negative and varies between -11.9 and -0.5 E, with a mean of -5.7 E and a standard deviation of 3.5 E. The absolute gravity gradient maxima are situated in central Tibet, while the corresponding minima are in the Sichuan, Tarim, Qaidam and Indo-Gangetic basins. The VMM isostatic gravity gradient is shown in Fig. 4. It varies between 14.2 and 2.3 E, with a mean of 8.6 E and a standard deviation of 3.4 E. The pattern of the isostatic gravity gradient is very similar to the consolidated crust-stripped gravity gradient, while having opposite sign.
2. VMM Moho model
The values of the isostatic gravity gradient (shown in Fig. 4) were used to solve the VMM inverse problem for finding the Moho depth within the study area on a 1×1 arc-deg grid. The system of observation equations was formed by discretizing the integral equation in Eq. (12). The zero-order Tikhonov (1963) regularization was applied to stabilize the solution. The inversion scheme with the regularization parameter α was described in the following vector-matrix form
where A is the design matrix of the discretized integrals (i.e., the right-hand side of Eq. 12); Δŝ is the parameter vector of the unknown Moho-depth parameters ds ; the regularization matrix R is the identity matrix I , i.e. R≡I ; and I is the vector of observables consisting of values of the isostatic gravity gradient. The solution to the system of observation equations in Eq. (21) for finding the unknown Moho-depth parameters ds was carried out iteratively using the Gauss-Seidel method (e.g., Young 1971). A priori error model was not applied. The stopping criterion of the convergence between the results of two successive steps (k and k+1) was set based on the following condition:‖s(k+1) - s(k)‖2= ‖dŝ (k+1)‖2≤ c, where c is a limit of convergence. The iteration stopped when the relative differences between two successive solutions reached 0.1%. The choice of the regularization parameter was based on minimizing the RMS of differences between the gravimetric and seismic models. In this way, we selected the regularization parameter for the gravimetric solution which had the best RMS fit with the CRUST1.0 Moho depths.
The result is shown in Fig. 5. The VMM Moho depths, determined within the study area, vary between 44.0 and 66.9 km, with a mean of 56.2 km and a standard deviation of 5.8 km. The most pronounced pattern of the Moho geometry is a significant contrast between the crustal thickness of orogenic formations compared to continental sedimentary basins. The largest crustal thickness is detected beneath Himalayas and Tibetan Plateau; the Moho depths there typically exceed 60 km. The Moho depths substantially decrease to less than 50 km in the Sichuan, Tarim, Qaidam and Indo-Gangetic basins.
To model the differences between the isostatic and seismic Moho models, we further applied the non-isostatic correction into the isostatic gravity gradient. The non-isostatically corrected gravity gradient data were then used to refine the VMM Moho solution. The non-isostatic corrections to the isostatic gravity gradient and to the Moho depths are shown in Fig. 6. The former varies between -2.4 and 3.1 E, with a mean of 0.3 E and a standard deviation of 1.0 E (see Fig. 6a). The latter is between -6.8 and 8.0 km, with a mean of 2.3 km and a standard deviation of 3.2 km (see Fig. 6b). The VMM Moho depths corrected for the non-isostatic effect are shown in Fig. 7. These Moho depths vary between 31.1 and 67.9 km, with a mean of 54.2 km and a standard deviation of 7.5 km. The application of the non-isostatic correction changed significantly a spatial pattern of the Moho geometry (compare Figs. 5 and 7). The most noticeable changes are related to the maximum Moho depths in central Tibet and less pronounced contours of the crustal thickness between orogens and sedimentary basins.
3. Correlation analysis
We investigated the spatial correlation of the consolidated crust-stripped gravity gradient with the non-isostatically corrected and uncorrected Moho geometry. The scatter plots are shown in Fig. 8. As seen in Fig. 8a, the consolidated crust-stripped gravity gradient has a systematic trend with respect to the VMM Moho depths. The largest (absolute) values of this gravity gradient correspond with the largest spatial variations of the Moho geometry under orogens attributed to a high correlation of the consolidated crust-stripped gravity disturbances with the Moho geometry (cf. Tenzer et al. 2012c). The application of the non-isostatic correction to the VMM Moho depths changed the spatial correlation between investigated quantities, especially under orogens (cf. Fig. 8b). To explain this spatial behavior, we further investigated the relation between the non-isostatic correction with the non-isostatically corrected and uncorrected Moho geometry. The scatter plots are shown in Fig. 9. Whereas there is no apparent correlation of this correction with the uncorrected Moho depths (see Fig. 9a), the non-isostatic correction is highly corrected with the corrected Moho geometry (see Fig. 9b). The application of this correction thus significantly changed the spatial pattern of the Moho geometry; it increased the crustal thickness in central Tibet and decreased beneath most of sedimentary basins. This is also evident from the relation between the non-isostatic gravity gradient correction and the corresponding changes of the Moho geometry (see Fig. 10). The largest (absolute) values of the non-isostatic gravity gradient correction typically correspond with the largest changes of the Moho geometry. From these findings we can conclude that the purely isostatic model significantly underestimates the crustal thickness of the orogenic formations, while overestimates the crustal thickness of continental sedimentary basins.
It is worth mentioning that the errors in the gravimetrically determined Moho depths attributed to the commission and omission errors of the global geopotential model are much smaller than the Moho errors caused by the uncertainties in the CRUST1.0 crustal structure model (Bagherbandi et al. 2014). The constraining information on the crustal density structure from seismic data is thus essential for the combined gravimetric-seismic Moho recovery, while the accuracy of the currently available global gravity models is sufficient.
4. Validation of results
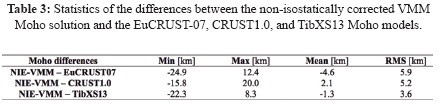
Both regional Moho solutions were compared with the EuCRUST07 (Tesauro et al. 2008, Stolk et al. 2013), CRUST1.0 (Bassin et al. 2000) and TibXS13 (Tenzer et al. 2013) Moho models. The EuCRUST07, CRUST1.0 and TibXS13 Moho models at the study area are shown in Figs. 10-13; statistics are summarized in Table 1. The differences between the VMM Moho solution (shown in Fig. 5) and these three Moho models are shown in Fig. 14; statistics of differences are given in Table 2. The same compassion was done for the non-isostatically corrected VMM Moho solution (shown in Fig. 7). The Moho depth differences are shown in Fig. 15 and the corresponding statistics are summarized in Table 3.
As seen from the comparison in Tables 2 and 3, the application of the non-isostatic correction slightly improved the RMS fit of the VMM Moho model with the CRUST1.0 and EuCRUST07, while decreased significantly when compared with TibXS13. The most significant change after applying the non-isostatic correction is seen in a substantial reduction of the systematic bias of the VMM Moho solution relative to the CRUST1.0 and TibXS13 Moho models. The systematic bias between the VMM and EuCRUST07 Moho models increased in the absolute sense.
Summary and concluding remarks
We have utilized the VMM isostatic scheme for a determination of the Moho geometry from the gravity gradient data. The gravimetric forward modeling of the isostatic gravity gradient was realized in a frequency domain based on applying the spherical harmonic analysis and synthesis of the global gravity and crustal structure models. The regional Moho inversion was realized in a frequency domain. The non-isostatic correction was applied to combine the isostatic and seismic Moho models.
The results of the gravimetric forward modeling showed that the maxima of the consolidated crust-stripped gravity gradient correspond with the largest spatial variations of the Moho geometry, revealing mainly the contrast in the crustal thickness between the orogens and continental sedimentary basins.
The VMM isostatic gravity gradient correction has a similar magnitude as the consolidated crust-stripped gravity gradient, while opposite sing. Both gravity gradient quantities have a similar spatial distribution.
The range of the consolidated crust-stripped gravity gradient is 11.4 E. The isostatic gravity gradient has a similar range of values of 11.9 E. This indicates that the gravity gradient field approximates realistically a relative geometry of the Moho interface. Hoverer, the refined gravity gradient field is systematically biased compared to the isostatic gravity gradient field; the difference between (absolute) mean values is 2.9 E.
The results of the gravimetric Moho inversion revealed how the systematic bias in the gravity gradient data propagates into the VMM Moho solution. To remove the systematic bias in the regional Moho model, we introduced and applied the non-isostatic gravity gradient correction for combining the isostatic and seismic Moho models. This correction also accounts for the unmodelled heterogeneous sub-crustal density structures, uncertainties of applied crustal model and geodynamic processes which cannot be modeled by the adopted isostatic scheme.
The application of the non-isostatic correction changed significantly the Moho geometry. The spatial geometry of the non-isostatic correction indicates that the largest discrepancies between the VMM isostatic and seismic Moho models at the study area are likely attributed to the active tectonic and crustal flexure.
Acknowledgments:
The Swedish National Space Board (SNSB) is cordially acknowledged for a financial support of M. Bagherbandi and L.E. Sjöberg by project No. 76/10:1 and 116/12. P. Novák was supported by the project 209/12/1929 of the Czech Science Foundation. We also acknowledge the research founding for foreign experts provided to R. Tenzer by the Chinese Ministry of Education.
References
Arabelos, D., G. Mantzios, and D. Tsoulis, 2007: Moho depths in the Indian Ocean based on the inversion of satellite gravity data. Adv. Geoscien., 9: Solid Earth, Ocean Science and Atmospheric Science, (Eds.) Huen W., Chen Y.T., World Scientific Publishing, pp. 41-52. [ Links ]
Bagherbandi, M., 2011: An Isostatic Earth Crustal model and Its Geodetic Applications. Unpublished PhD thesis. Royal Institute of Technology. [ Links ]
Bagherbandi, M., and M. Eshagh, 2012: Recovery of Moho's undulations based on the Vening Meinesz-Moritz theory from satellite gravity gradiometry data: A simulation study. Adv. Space Res., 49, 1097-1111., doi:10.1016/j.asr.2011.12.033. [ Links ]
Bagherbandi, M., and L. E. Sjöberg, 2012: Non-isostatic effects on crustal thickness: A study using CRUST2.0 in Fennoscandia. Phys. Earth Planet. Inter., 200-201, 37-44. [ Links ]
Bassin, C., G. Laske, and G. Masters, 2000: The current limits of resolution for surface wave tomography in North America. Eos, Trans., AGU, 81, F897. [ Links ]
Braitenberg, C., and M. Zadro, 1999: Iterative 3D gravity inversion with integration of seismologic data. Boll. Geof. Teor. Appl., 40, 3/4, 469-476. [ Links ]
Braitenberg, C., M. Zadro, J. Fang, Y. Wang, and H. T. Hsu, 2000a: Gravity inversion in Qinghai-Tibet plateau. Phys. Chem. Earth, 25, 381-386, doi: 10.1016/S1464-1895(00)00060-0. [ Links ]
Braitenberg, C., M. Zadro, J. Fang, Y. Wang, and H. T. Hsu, 2000b: The gravity and isostatic Moho undulations in Qinghai-Tibet plateau. J. Geodyn., 30, 489-505, doi: 10.1016/S0264-3707(00)00004-1. [ Links ]
Braitenberg, C., S. Wienecke, and Y. Wang, 2006: Basement structures from satellite-derived gravity field: south China Sea ridge. J. Geophys. Res., 111, B05407. [ Links ]
Braitenberg, C., P. Mariani, M. Reguzzoni, and N. Ussami, 2010: GOCE observations for detecting unknown tectonic features. In: Proc. of the ESA Living Planet Symposium, 28 June - 2, July 2010, Bergen, Norway, ESA SP-686. [ Links ]
Čadek, O. and Z. Martinec, 1991: Spherical harmonic expansion of the earth's crustal thickness up to degree and order 30. Stud. Geophys. Geod., 35, 151-165. [ Links ]
Eshagh, M., 2014: Determination of Moho discontinuity from satellite gradiometry data: linear approach. Geodyn. Res. Int. Bull., 1, 2,1-13. [ Links ]
Hinze, W. J., 2003: Bouguer reduction density, why 2.67? Geophysics, 68, 1559-1560, doi: 10.1190/1.1620629. [ Links ]
Mayer-Guerr T., D. Rieser, E. Höck, J. M. Brockmann, W. - D. Schuh, I. Krasbutter, J. Kusche, A. Maier, S. Krauss, W. Hausleitner, O. Baur, A. Jäggi, U. Meyer, L. Prange, R. Pail, T. Fecher, and T. Gruber, 2012: The new combined satellite only model GOCO03s. Presented at GGHS2012, Venice, October. [ Links ]
Moritz, H., 2000: Geodetic Reference System 1980. J. Geod., 74, 128-162. [ Links ]
Novák, P., and R. Tenzer, 2013: Gravitational gradients as a tool for probing the Earth's structure. Surv. Geoph., doi: 10.1007/s10712-013-9243-1. [ Links ]
Pavlis, N. K., J. K. Factor, and S. A. Holmes, 2007: Terrain-related gravimetric quantities computed for the next EGM. Presented at the 1st International symposium of the International gravity service 2006, August 28 - September 1, Istanbul, Turkey. [ Links ]
Reguzoni, M., and D. Sampietro, 2012: Moho estimation using GOCE data: A numerical simulation. In: Geodesy for Planet Earth International Association of Geodesy Symposia, 136, pp. 205-214. [ Links ]
Sampietro, D., M. Reguzzoni, and C. Braitenberg, 2013: The GOCE estimated Moho beneath the Tibetan Plateau and Himalaya. In: International Association of Geodesy Symposia, Earth on the Edge: Science for a Sustainable Planet, Proceedings of the IAG General Assembly, 28 June - 2 July 2011, Melbourne, Australia, Rizos, C. and P. Willis (Eds.), Vol. 139, Springer-Verlag, Berlin. [ Links ]
Sampietro, D., 2011: GOCE exploitation for Moho modelling and applications. In: Proceedings of the 4th international GOCE user workshop, Munich, Germany,Vol. 31. [ Links ]
Sjöberg, L. E., 2009: Solving Vening Meinesz-Moritz inverse problem in isostasy. Geophys. J. Int., 179, 1527-1536, doi: 10.1111/j.1365-246X.2009.04397.x. [ Links ]
Sjöberg, L. E. and M. Bagherbandi, 2011: A method of estimating the Moho density contrast with a tentative application of EGM08 and CRUST2.0. Acta Geophys., 59, 502-525, doi: 10.2478/s11600-011-0004-6. [ Links ]
Sjöberg, L.E., 2013: On the isotactic gravity anomaly and disturbance and their applications to Vening Meinesz-Moritz gravimetric inverse problem. Geophys. J. Int., doi: 10.1093/gji/ggt008. [ Links ]
Stolk, W., M. K. Kaban, F. Beekman, M. Tesauro, W. D. Mooney, and S. A. P. L. Cloetingh, 2013: Tectonoph., in press, accepted paper, available online since 31 January 2013 from the Tectonophysics web site. [ Links ]
Tenzer, R., Hamayun, and P. Vajda, 2009: Global maps of the CRUST2.0 crustal components stripped gravity disturbances. J. Geophys. Res., 114, B, 05408. [ Links ]
Tenzer, R., P. Novák, and V. Gladkikh, 2011: On the accuracy of the bathymetry-generated gravitational field quantities for a depth-dependent seawater density distribution. Studia Geophys. Geodaet., 55, 4, 609-626. [ Links ]
Tenzer, R., and M. Bagherbandi, 2012: Reformulation of the Vening-Meinesz Moritz inverse problem of isostasy for isostatic gravity disturbances. Inter. J. Geoscien., 3, 5, 918-929. [ Links ]
Tenzer, R., P. Novák, P. Vajda, V. Gladkikh, and Hamayun, 2012a: Spectral harmonic analysis and synthesis of Earth's crust gravity field. Comput. Geosc., 16, 1, 193-207. [ Links ]
Tenzer, R., V. Gladkikh, P. Vajda, and P. Novák, 2012b: Spatial and spectral analysis of refined gravity data for modelling the crust-mantle interface and mantle-lithosphere structure. Surv. Geoph., 33, 5, 817-839. [ Links ]
Tenzer, R., M. Bagherbandi, Ch. Hwang, and E. T. Y. Chang, 2013: Moho interface modeling beneath Himalayas, Tibet and central Siberia using GOCO02S and DTM2006.0. In: Special issue on geophysical and climate change studies in Tibet, Xinjiang, and Siberia from satellite geodesy. Terr. Atm. Ocean. Scie., doi: 10.3319/TAO.2012.11.01.02 (TibXS). [ Links ]
Appendix A: Gravimetric forward modeling
Tenzer et al. (2012a) developed and applied a uniform mathematical formalism of computing the gravity corrections. It utilizes the expression for the gravitational potential V generated by an arbitrary volumetric mass layer with a variable depth and thickness while having laterally distributed vertical mass density variations. For a computation point (r,Ω), it reads
where GM=3986005×108 m3 s-2 is the geocentric gravitational constant. The potential coefficients Vn,m in Eq. (A.1) are defined as
where 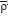 Earth =5500kg/m3 is the Earth's mean density (cf. Novák 2010). The numerical coefficients {F1(i)n,m,Fu(i)n,m:i0,1...,I} are given by
Earth =5500kg/m3 is the Earth's mean density (cf. Novák 2010). The numerical coefficients {F1(i)n,m,Fu(i)n,m:i0,1...,I} are given by
The terms  and
and  define the spherical lower-bound and upper-bound laterally distributed radial density variation functions Ln and Un of degree n. These numerical coefficients combine the information on the geometry and mass density (or mass density contrast) distribution within a volumetric layer. The computation of these coefficients is realized to a certain degree of spherical harmonics using discrete data of the spatial density distribution (typically provided by means of density, depth and thickness data) of a particular structural component of the Earth's interior. The spherical functions Ln and Un, and their higher-order terms {
define the spherical lower-bound and upper-bound laterally distributed radial density variation functions Ln and Un of degree n. These numerical coefficients combine the information on the geometry and mass density (or mass density contrast) distribution within a volumetric layer. The computation of these coefficients is realized to a certain degree of spherical harmonics using discrete data of the spatial density distribution (typically provided by means of density, depth and thickness data) of a particular structural component of the Earth's interior. The spherical functions Ln and Un, and their higher-order terms { } are generated using the following integral convolutions
} are generated using the following integral convolutions
The heights/depths DU and DL of the upper-bound and lower-bound of the volumetric mass density layer are stipulated with respect to the sphere of radius R. For a specific volumetric layer, the mass density ρ is either constant ρ, laterally-varying ρ (Ω') , or - in the most general case - approximated by a 3-D density model. For each lateral column {Ω':Ω'∈Φ}, we have
The nominal value of the lateral density ρ(DU,Ω') is stipulated at DU. This density distribution model describes the radial density variation (by means of the coefficients { α:i = 1,2,...,I} and β ) within the volumetric mass layer at a location Ω' . Alternatively, when modeling the gravitational field of anomalous density structures, the density contrast Δρ of a volumetric mass layer relative to the reference density ρc is defined as
where Δρ(DU,Ω') is the nominal value of the lateral density contrast stipulated at DU. Here the reference density ρc of the homogenous crust was used.
Appendix B: Consolidated crust-stripped gravity gradient
The consolidated crust-stripped gravity Tcsrr gradient is obtained from the corresponding gravity gradient component Trr after applying the topographic and crust density contrasts stripping gravity gradient corrections. The computation is realized according to the following scheme (Tenzer et al. 2012b)
where  and Vcrr are, respectively, the gravitational gradients generated by the topography and density contrasts of the ocean (bathymetry), ice, sediments and remaining anomalous density structures within the consolidated (crystalline) crust.
and Vcrr are, respectively, the gravitational gradients generated by the topography and density contrasts of the ocean (bathymetry), ice, sediments and remaining anomalous density structures within the consolidated (crystalline) crust.
The radial gravity gradient Vrr at a point (r, Ω) is computed as
where Tn,m are the (fully-normalized) numerical coefficients which describe the disturbing gravity potential T (i.e., the difference between the Earth's and normal gravity potentials). The coefficients Tn,m are obtained from the coefficients of a global geopotential model (describing the Earth's gravity field) after subtracting the spherical harmonic coefficients of the normal gravity field.
The computation of the gravity gradient corrections in terms of the potential coefficients Vn,m (see Eq. A.2) for a particular structural component of the Earth's crust  is realized using the following expression
is realized using the following expression