1. Introduction
Determining the gravity field with as much accuracy as possible is significant for earth sciences such as geodesy and geophysics, and the gravity field is instrumental in many natural incidents related to earth dynamics, primarily mass transportation. In recent years, research conducted to determine the earth's gravity field has gained speed thanks to Low Earth Orbits (LEO). Various Global Geopotential Models (GGMs) have been released using in particular CHAMP (CHAllenging Minisatellite Payload), GRACE (Gravity Recovery And Climate Experiment) and GOCE (Gravity field and steady-state Ocean Circulation Explorer) orbit data. These models have a positive impact on determining geoid changes.
Launched from Russia's Plesetsk spaceport on 15 July 2000, CHAMP was the first low earth satellite launched in order to determine gravity field. The CHAMP mission was carried out by the Potsdam (Germany) Earth Research Center (GeoForschungsZentrum-GFZ). The satellite is almost circular and located close to the pole, with 454 km starting height and 87.3° inclination degree. Although its work period was planned to be five years, it operated until 19 September 2010. The core aims to be reached through the CHAMP satellite are to specify long wavelength features of the statical earth's gravity field (and partially time changes) with the greatest possible accuracy, mapping the global magnetic field, which means specifying the earth's primary magnetic field and its time changes, and to reveal ionosphere and troposphere profiles, respectively (Seeber 2003; Hofmann-Wellenhof and Moritz 2005). CHAMP satellite was groundbreaking in specifying long wavelength components of the gravity field. Compared to GRIM5-S1 and EGM96S models produced by several observations and satellites, it has been found that gravity field resolution is higher specified with a couple of month's old CHAMP orbit tracking data (Reigber et al. 2003).
GRACE mission is the continuing part of the CHAMP satellite. Unlike CHAMP, it consists of two identical satellites following each other on the same orbit with 220 km ± 50 km distance between them. Both satellites were launched simultaneously from the Russian Plesetsk spaceport on 17 March, 2002. GRACE mission is a product of a joint project of DLR (Deutsches Zentrum für Luft-und Raumfahrt) and NASA (U.S. National Aeronautics and Space Administration). University of Texas, Center for Space Research (CSR) was assigned as the project principal. Like CHAMP, data are needed that are homogeneously distributed and surrounding the earth entirely, in order to obtain a sensitive projection of gravity potential. Therefore, the GRACE mission is close to the pole and almost circular. Initial orbit height was selected at around 500 km, and the orbit tendency 89°. Aim of GRACE mission is to determine the earth's high resolution global gravity field and time changes in this field. These satellites are also used in order to map Total Electron Content (TEC) as in the CHAMP satellite mission (Hofmann-Wellenhof and Moritz 2005; Jâggi 2007). Resolution of the gravity field based on GRACE data is better than the previous ones. According to Tapley et al. (2004), it was found that improvements in the global gravity field were significant compared to GGM01S earth gravity model EGM96 determined by 110-day GRACE data.
GOCE mission is the core project of the Living Planet Programme of the European Space Agency (ESA). GOCE satellite is the last in the satellite series launched to determine gravity field. Orbit of GOCE satellite was launched from the Russian Plesetsk spaceport on 17 March 2009 as almost circular and solar-synchronized. Orbit height was selected as 250 km in order to get a stronger and more sensitive gravity signal. Monitoring and controlling the satellite were carried out by ESA/ESOC in collaboration with earth stations Kiruna in Sweden, and Svalbard in Norway. Main objective of GOCE is to participate in measuring the earth's gravity field and modelling the geoid with perfect accuracy and spatial resolution. Anticipated accuracies are determining gravity-field anomalies with 1mGal (10-5 ms-2), geoid with 1-2 cm accuracy, and reaching a spatial grid resolutions better than 100 km.
Many researchers have investigated the contribution of GGMs produced from CHAMP, GRACE, and GOCE satellites in local and global geoid models for various areas of the earth (Amos and Featherstone 2003; Kiamehr and Sjõberg 2005; Rodriguez-Caderot et al. 2006; Benahmed Dahoa et al. 2006; Ustun and Demirel 2006; Erol et al. 2009; Kotsakis and Katsambalos 2010; Yilmaz et al. 2010; Janak and Pitonak 2011; Gikas et al. 2013; Godah and Krynski 2013; Soycan 2014). Various methods and approaches have been suggested as a result of the above-mentioned research. One of the most frequently employed methods in the literature to determine the best GGM for an area's gravity field is comparing GGMs and revealing their performance through independent datasets (GNSS/ levelling, gravity etc).
In this research, the geoid undulation values are calculated through GGMs (69 GGMs at the time of writing this paper) for a 210 km long strip project. Then these values are compared to accurate geoid undulation values calculated with GNSS/levelling method. As a result, performance of GGMs is revealed statistically and the best GGM is suggested. Moreover, investigation of possible maximum geoid accuracy to be obtained from GGMs is aimed at in this research employing only geographical latitude and longitude information of points without any geodetic measuring in the field.
2. Theoretical Background
2.1. Global Geopotential Models (GGMs) and GNSS/levelling
The sum of centrifugal and gravity forces on an object is defined as gravity force. Determining the earth's gravity field is the same as determining its potential. As this potential is harmonical out of masses that form the earth, spherical harmonic series are generally used for determining the gravity field (Kaula 1966; Heiskanen and Moritz 1984; Rummel et al. 2002; Seeber 2003; Hofmann-Wellenhof and Moritz 2005).
Global Geopotential Models (GGMs) are defined as spherical harmonic coefficients representing the earth's gravity field in various wavelengths. These coefficients are obtained from satellite orbit deviation analyses, satellite altimeter data, gravity gradiometer data, and gravimeter data. GGMs are divided into three groups in this context (Vanicek and Featherstone 1998; Featherstone 2002).
• Satellite-only models: Coefficients of these GGMs are derived from orbit deviation analyses of artificial earth satellites. Degree of these models is low, and resolution is insufficient.
• Combined models: The combined GGMs are produced by combining gravity data derived from satellite data, terrestrial gravity observations, airborne gravimetry and satellite altimeter data in marine areas. Therefore, integrated models have higher degrees and produce more accurate results compared to satellite-only models.
• Tailored models: These models are generated as a result of improving harmonic coefficients of GGMs using special mathematical techniques within the first and second groups. The main aim of these models is to increase the degree of the model.
Improving measurement, calculation and evaluation techniques have contributed to constant improvement of GGMs. This improvement causes enhanced geoid resolution. In other words, when the degree of GGMs increased, errors of the deflection of the plumb line, gravity anomaly, and height anomaly are decreased, and the better the determination of the geoid (Wenzel 1998). GGMs point out the gravity field of the earth with spherical harmonic series. According to this the geoid height of a point the spherical geocentric coordinates of which are known might be calculated with Eq. (1) (Hofmann-Wellenhof and Moritz 2005).
where r, θ, λ are the spherical geocentric coordinates of the computation point: radial distance, co-latitude and longitude, respectively, GM is the gravitational constant (G) times mass (M) of the earth, у is mean normal gravity of the reference ellipsoid, R is the mean earth's equatorial radius,  are fully normalized geopotential coefficients with degree n and order m,
are fully normalized geopotential coefficients with degree n and order m,  nm(cos θ) fully normalized associated Legendre functions, and nmax is the maximum degree of the GGM.
nm(cos θ) fully normalized associated Legendre functions, and nmax is the maximum degree of the GGM.
In order to determine the optimum GGM for an area's gravity field, geoid heights derived from the GNSS/levelling method could be compared to the geoid heights calculated by GGMs (Amos and Featherstone 2003; Kılıçoğlu et al. 2009; Yilmaz et al. 2010; Hirt 2011; Guimarães et al. 2012). In many GNSS applications users feel a need for transformation between ellipsoidal height and orthometric height. The main reason of this is using orthometric heights in engineering, determined by levelling, and the difficulty of making levelling measurements for each point. Highly precision geoid models are needed for this type of implementation. Geoid height (undulation) values produced based on GNSS/levelling measurements are necessary to determine sensitively to this end (Doganalp and Selvi 2015). According to the GNSS/levelling method, geoid undulation value at a point is calculated with Eq. (2) (Heiskanen and Moritz 1984).
Here N stands for geoid height (undulation), h for ellipsoidal height obtained from GNSS measurements, and H for orthometric height calculated after levelling measurements. To evaluate the quality of GGM-derived geoid undulation values (Nggm) many independent NGNSS/lev values could be used that are spread over the project area. Therefore, absolute geoid height differences AN might be calculated with Eq. (3) (Kotsakis and Sideris 1999; Fotopoulos et al. 2003; Huang and Véronneau 2004; Gikas et al. 2013).
3. Applications
3.1. Study area and data
Study field is the High-Speed Train route between Konya-Polatli (Ankara), which is 210 km long. There are 110 GNSS/levelling points (benchmarks) within the project field. Orthometric heights (H) of the points were determined with the geometric levelling method in the datum of the Turkey National Vertical Network (TUDKA). The geographic coordinates including ellipsoidal heights (h) were determined in static positioning mode and referred to the Turkish National Fundamental GPS Network (TUTGA). The orthometric and ellipsoidal height of the points within the study field are varying between 696 - 1198 m and 733 - 1234 m respectively. Also, the geoid heights are varying between 36.72 and 37.70 m (Fig. 1). The minimum, maximum and mean values of distance between sequential points of the route were observed as 1.05, 5.53 and 1.94 km respectively. SRTM-3 data and The Generic Mapping Tools (GMT) software were used to draw Figure 1 (Wessel and Smith 1998). The Shuttle Radar Topography Mission (SRTM) contains elevation data with 3 arc-second resolution and 16 m absolute height error (90 percent confidence level). These data are available with free of charge via the Internet for approximately 80 percent of the earth's land mass (Bildirici et al. 2009).
3.2 Evaluation Procedure
A total of 69 models were used to investigate the quality of GGMs. In order to display the results from those models clearly, GGMs are classified in three models derived from CHAMP, GRACE, and GOCE satellites. Spherical harmonic coefficients of all models were obtained from the International Centre for Global Earth Models (ICGEM) web page. In addition, geoid heights based on GGMs can be calculated using coefficients and software on this website. Within the scope of implementation, in order to include all of Turkey, separate grid networks (grid step is 0.1o x 0.1o) were established for each GGM. GRS80 elipsoid parameters were used to establish grids. A correction needs to be applied on the difference between the true potential of the geoid and the normal potential of GRS80 when calculating geoid height, when using GRS80 as the chosen reference field. The reason for this correction is the difference between the GM value estimated for earth and the GM value for GRS80 elipsoid. Therefore, the "zero-degree" term based on different GM values needs to be considered in geoid height computation (Smith 1998). In addition, while the shape of the geoid depends on the permanent tide system type (mean, zero and tide-free), the values oftrue gravity potential do not change when one system transform another system. Therefore, the tide-free geoid model is suggested to be used in conversion of the GNSS heights (Smith 1998). Thus, correction term (zero degree term) has been applied to all calculations within the context of this application, and tide-free model is used as the tide system. In each of the GGM grid nets established, geoid heights of project points are interpolated using a script.
GGMs based on CHAMP
In this section, the results on GGMs for 110 points of the study area produced based on CHAMP are addressed. Totally 17 CHAMP-based global geopotential models are used. Names, production years, degrees and the data used to produce them are given in Table 1. Geoid undulations within study area are estimated using these models. The statistics of the differences between the GNSS-based and the GGM-based geoid undulations are given in Table 2 and Figure 2.
Table 2 Statistics of geoid height differences between GGM-derived (Nggm) and GNSS/levelling (NGNSS/lev) data, units in meters (based on CHAMP)
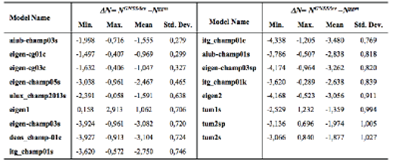
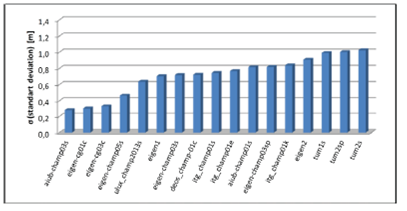
Fig. 2 The standard deviations of geoid undulation differences between GNSS/levelling and GGMs (based on CHAMP)
Table 2 and Figure 2 show the standard deviation values range between 0.28 - 1.03 m with regard to geoid undulation differences. Moreover, the best five models for CHAMP-based GGMs are aiub-champ03s, eigen-cg01c, eigen-cg03c, eigen-champ05s and ulux_champ2013s, respectively.
GGMs based on GRACE
In this section, 24 global geopotential model evaluations have been done using GRACE-based models. Information on GGMs is given in Table 3. Performance of GGMs determined after evaluation of 110 points within the project field is shown in Table 4. Moreover, the diagram displaying the differences between geoid heights calculated by GGMs and the known heights of GNSS/levelling points is given in Figure 3.
Table 4 Statistics of geoid height differences between GGM-derived (Nggm) and GNSS/levelling (NGNSS/lev) data, units in meters (based on GRACE)
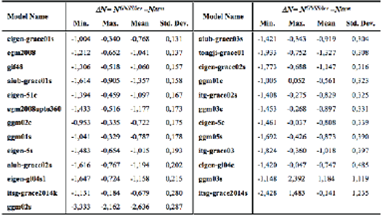
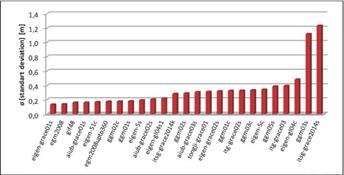
Fig. 3 The standard deviations of geoid undulation differences between GNSS/levelling and GGMs (based on GRACE)
Table 4 and Figure 3 show the standard deviation values range between 0.13 - 1.24 m according to geoid undulation differences. Lower standard deviation values are reached compared to CHAMP-based models. In addition, the best first five models for GRACE-based GGMs are eigen-grace01s, egm2008, gif48, aiub-grace01s and eigen-51c, respectively.
GGMs based on GOCE
In this section, 28 global geopotential models are evaluated based on the GOCE satellite. Information on GOCE-based GGMs is given in Table 5. Performance of GGMs within the study area is shown in Table 6. Moreover, the diagram displaying the standard deviation of differences between geoid heights calculated by GGMs, and the known heights of GNSS/levelling points is given in Figure 4.
Table 6 Statistics of geoid height differences between GGM-derived (Nggm) and GNSS/levelling (NGNSS/lev) data, units in meters (based on GOCE)
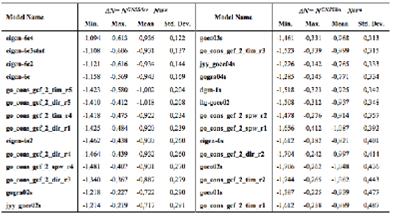
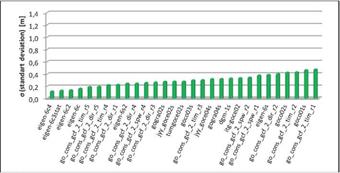
Fig. 4 The standard deviations of geoid undulation differences between GNSS/levelling and GGMs (based on GOCE)
Table 6 and Figure 4 show the standard deviation values range between 0.12 - 0.49 m with regard to geoid undulation differences. These values might be considered good compared to CHAMP and GRACE-based models. Moreover, the best first five models for GOCE-based GGMs are eigen-6c4, eigen-6c3stat, eigen-6c2, eigen-6c and go_cons_gcf_2_tim_r5, respectively.
Best GGMs in the study area
In order to summarize the results of all the implementations, five GGMs obtained from implementations conducted in three classes are evaluated. Table 7 contains the best five GGMs according to geoid undulation differences within every class. Figure 5 shows the performance of GGMs using the standard deviation values calculated in Table 7.
Table 7 Statistics of geoid height differences between GGM-derived (Nggm) and GNSS/levelling (NGNSS/lev) data, units in meters.
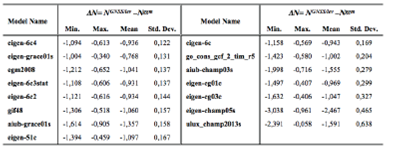
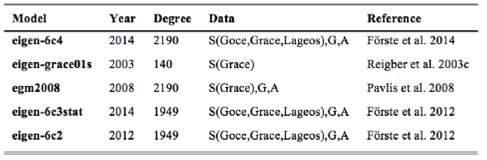
Table 7 and Figure 5 show the best GGM for the study area is eigen-6c4. This model is followed by eigen-grace01s, egm2008, eigen-6c3stat and eigen-6c2, respectively. Considering the performance of these models, there is no large difference between them with regard to standard deviation values. In addition to this, general characteristics of models show that all the models except eigen-grace01s have a considerable degree, and gravity and altimeter data make positive contributions to the model (Table 8).
Table 8 The best five global geopotential models in the study area (S: Satellite, G: Gravity, A: Altimetry)
Differences between GNSS/levelling-based geoid heights and GGM-based geoid heights are influenced by datum inconsistencies and systematic errors. Therefore, different parametric models could be used in order to minimize these values (bias and tilt) (Kotsakis and Katsambalos 2010; Yilmaz et al. 2010). Generally, three, four, five and seven parametric models are used for the least-squares adjustment of the geoid height differences in the literature. Therefore, these parametric models were tested in this paper.
Geoid Heights Determination using Different Parametric Models
Systematic errors such as datum shifts and distortion among height systems might be minimized using the Least Squares Adjustment (LSA) model. If Eq. (3) is edited with this aim
is obtained (Kotsakis and Sideris 1999; Kiamehr and Sjõberg 2005). Here ai stands for known coefficients vector, x unknown parameters vector, and vi a residual random noise term. Four different parametric models (3, 4, 5 and 7-parameters) are used within the context of application. Mathematical statements for these models are as below, respectively (Kotsakis and Katsambalos 2010).
where xi transformation parameters between two datums, vi residual random noise term, (φi, λi) geodetic coordinates of points, e first eccentricity of the reference elipsoid, and  The matrix form is created as follows for the equations
The matrix form is created as follows for the equations
Where ai is the coefficients vector and x is unknown's vector for Model 4. For other parametric models, coefficients and unknowns vector might be formed as in Eq. (9). If the formed coefficients are expanded for each GNSS point, A coefficients matrix (design matrix) would be obtained to be used in LSA (Eq. 10). Afterwards, unknown parameters can be solved with LSA.
Table 9 and Figure 6 show the statistical values obtained with 3, 4, 5, and 7-parameter LSA implementation of the best five GGMs reached as a result of application. Table 9 and Figure 6 also show the best results obtained from the eigen-6c2 model. Moreover, the 7-parameter transformation model gives results that are the most compatible with minimum standard deviation values when compared to other parametric models. Figures 7-11 show the geoid heights after implementing transformation and geoid heights obtained from GGMs with GNSS/levelling geoid heights.
Table 9 Statistics of the differences between geoid heights obtained from GGMs and from GNSS/levelling data after applying the 3-, 4-, 5- and 7-parameter transformation, units in meters
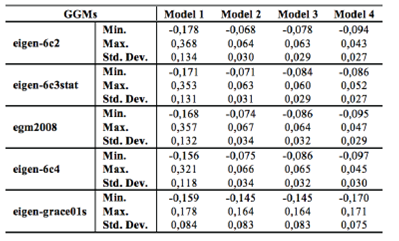
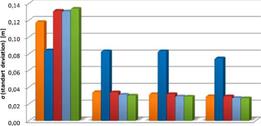
Fig. 6 The standard deviations of geoid undulation differences between GNSS/levelling and GGMs after transformations
When the Figures 7-11 were examined, it has seen that there were a jump for the first geoid height values calculated from GGMs and the datum shift. The reason for these effects is thought to be systematic errors. Therefore, different parametric models could be used in order to minimize these effects. If the Figures are reviewed, it can be seen that these effects are minimized when the degree of parametric transformation is increased.
The parametric models describing the systematic errors and datum shifts in the different height data sets are used in the study. When the application results and the figures were examined, the 7-parameter transformation model gave results that are the most compatible with minimum standard deviation values when compared to other parametric models. Also, results show that eigen-6c2, eigen-6c3stat, eigen-6c4 and egm2008 global geopotential models produce approximately ±3 cm accuracy when compared to GNSS/levelling. Especially, 7-parameter transformation of eigen-6c2 and eigen-6c3stat models produces geoid height information with ±2.7 cm accuracy for 110 points within this test field. This accuracy obtained from GGMs can be seen adequate for several engineering applications. When the contributions of the new satellites going to be launched in the near future are considered, the accuracies obtained from GGMs will increase with each passing day. Thus, the use of GGMs for determining values such as the geoid height, the height anomaly, the gravity field etc. will play an important role in the earth sciences.
4. Conclusion and Suggestions
The aim of this study is to investigate the performance of GGMs produced by CHAMP, GRACE, and GOCE as well as comparing GGMs with GNSS/levelling data, and eventually to determine the best model. Within the scope of this study, the 210-km long Konya-Ankara high-speed train project was selected in order to investigate GGMs performance. When the study area is examined, it can be stated that the route has a flat ground and there is not a sudden height-change structure. While the orthometric height values of the points in the study area range between 696 and 1198 m, the ellipsoidal height 733 - 1234 m. 110 GNSS/levelling (benchmarks) points were included in the study area. Geoid heights of these points were calculated for all GGMs using only latitude and longitude of the points. Then these values were compared to true geoid heights and the performances of GGMs were examined.
According to results, the standard deviation was obtained as approximately 12 cm after comparing with true values of the geoid heights obtained from the best match GGMs. The best GGMs are obtained eigen-6c4, eigen-grace01s, egm2008, eigen-6c3stat, and eigen-6c2, respectively. High degrees of the GGM of all the models except for eigen-grace01s along with its different data variety (gravity and altimeter) contributed to improving geoid height information obtained from the models.
Systematic errors in GGMs such as datum shifts and distortions can be minimized using different parametric models. Therefore, these errors are minimized using four different parametric (3, 4, 5, and 7-parametric) models in the scope of the implementation. When were examined the results after transformation, 7-parameter model compared to other models were produced the better results. According to 7-parameter model results, the best five GGMs are eigen-6c2, eigen-6c3stat, egm2008, eigen-6c4 and eigen-grace01s. Standard deviation value obtained from GGMs is approximately 3 cm for the first four models and 8 cm for the eigen-grace01s model. Standard deviation value obtained from the eigen-graceOls is significantly higher compared to the other models. This is most probably related to the data, including only satellite observations, and lower degree (n max = 140) of the model.
According to the application results, it may be possible to use 3 cm-geoid height information for various engineering applications. It is obvious that geoid heights obtained from GGMs will be improved through developing technology and new satellite missions to be launched in the near future. It is also possible to conclude that after reaching 1-2 cm geoid height accuracy, height of points will be obtained with high accuracy using GGMs without the need for the levelling process in many engineering applications.

































