1. Introduction

Global Navigation Satellite System (GNSS) has been routinely used in several scientific and engineering applications including positioning, navigation and timing systems for many years. Traditional relative positioning method has been handled for GNSS-based positioning applications when high precision and accuracy are required. However, Precise Point Positioning (PPP) method, a state space solution to the processing of GNSS data acquired from a single receiver, has become an alternative to the relative positioning method by providing high absolute accuracy (^{Gao and Shen, 2001}; ^{Rizos et al., 2012}).

Traditionally, in all of the relative positioning methods depend on GNSS technique, simultaneous observations should be made at one or more reference points. In other words, minimum two or more GNSS receivers should be occupied at; one reference station, whose coordinates are known, and the other/s should be established to the point/s, whose coordinates will be estimated. However; in PPP technique to make observations on one point, whose coordinates will be estimated is enough for the estimation with one GNSS receiver using absolute positioning approach. With regard to this, PPP technique allows a significant advantage to the users in terms of time and budget saving (^{Ocalan, 2015}).

Many factors such as preferred positioning method (relative or absolute), survey mode (static or kinematic), observation duration, equipment, signals and codes, data processing algorithms, reference receiver/receivers utility, satellite-receiver geometry, post-processing analyses or real-time applications provide different levels of performance for GNSS positioning (^{Rizos et al., 2012}).

Several error sources affect positioning accuracy in GNSS surveys. Today relative techniques provide better solutions than PPP technique in terms of point positioning accuracy. The basic reason of this is that the effects of satellite orbit errors in relative techniques are lower than PPP technique. Moreover, clock errors can be eliminated in relative techniques using double differencing of phase measurements. However, these effects are quite significant and dominant error sources in PPP technique. Although relative positioning method removes some of these error sources either by applying phase differences techniques or by modeling of them, no modelled errors occurred in the forested areas, where especially satellite vision is limited, and orbital errors have significant effects on solutions (^{Hoffman-Wellenhof et al., 2001}). This is a significant problem for PPP method. Since precise satellite orbit and clock information are used, several error models are inevitable for PPP method.

Satellite visibility problem is the critical issue that should be taken into consideration for selection of the point location. It is required to ensure that there should not be any blockage or limitation of signals transmitted from satellite to receiver while establishing the points. This may cause problems at some of the engineering applications. At the applications where especially are performed around the forested areas, satellite vision has significant effects on positioning accuracy (^{Naesset, 1999}; ^{Pirti, 2005}; ^{Tachiki et al., 2005}; ^{Hasegawa and Yoshimura, 2007}; Pirti, 2008). The other significant problem is orbital errors. Several organizations such as IGS, JPL, CODE and NRCan present several data and products freely to the users to be used for decreasing or eliminating the orbital errors. These products are classified in terms of their accuracies as broadcast, ultra-rapid, rapid and final. IGS also presents some other standardized products such as satellite and station clocks, ionospheric and tropospheric parameters, besides satellite ephemerides.

The principle of GNSS method is based on resection problem using satellites, so satellite ephemerides are crucial on analyses. These orbit parameters have different levels of accuracy as seen in Table 1. Therefore, accuracies of the results have been altered according to the used product.

Table 1 GPS/GLONASS Satellite Ephemerides (URL-1, URL-4 and URL-6) 

In this study, it is aimed to investigate the accuracy of PPP method versus relative positioning especially around or under the forested areas (limited satellite visibility) considering the developments of PPP method and web-based online services. For this purpose, GNSS data collected at three points with long observational durations have been examined for static positioning and analyzed by different software and Web-based online services by selecting different satellite orbit products (ultra-rapid, rapid and final). These dataset was first processed manually using GIPSY-OASIS v6.3 software in PPP mode with JPL products, and then analyzed by the various Web-based online PPP services, namely CSRS-PPP, APPS, GAPS and Trimble-RTX. Moreover, the related dataset was processed manually by Bernese v5.2 software using CODE and IGS products (^{Dach et al., 2015}), and then evaluated by Web-based online services namely AUSPOS and OPUS. Hereby, we investigate the accuracy of PPP method versus relative positioning according to the outcomes of analysis, especially for the points established around the forested areas. Methods mentioned in this study use different satellite ephemerides provided from various services. AUSPOS, OPUS, GAPS and CSRS-PPP services use IGS products; APPS uses JPL products and Trimble RTX uses its own orbit products.

2. PPP Technique Versus Relative Positioning

GNSS users prefer relative positioning method in surveying applications if high accuracy is needed. All GNSS methods depending on relative positioning principle require simultaneous observations occupied at least one reference station whose coordinates are well known. Therefore, minimum two receivers should be used on surveys: one is busy at the reference station and the other is occupied at the point whose coordinates will be determined. The primary factors for point positioning accuracy are the baseline length between two receivers and the observation duration. In this context, establishing Continuously Operating Reference Stations (CORS) networks has a significant contribution to the relative positioning (^{Abd-Elazeem et al., 2011}; ^{Rizos et al., 2012}).

Relative positioning determines the point coordinates by using double differences on phase measurements as given below with Eq.1 (^{Hoffman-Wellenhof et al., 2001}):

Where is the double difference operator at the time of receiving data, ( is the phase measurement, (t) is the time of receiving data, (t-) is the satellite time, x is the travel time from the satellite to the receiver, r(t, t-) is the true geometric range, ds is the orbital prediction error, diono and dtropo are the ionospheric and tropospheric errors, respectively,is the wavelength, N is the integer phase ambiguity and is the noise components.

Scientific software is used for long baselines in post processing solutions of relative positioning, and commercial software is used for short baselines. The list of the most commonly known Web-based online services can be seen in Table 2.

Table 2 Web based online services using relative solution approach (URL-2, URL-3) 

PPP method is the particular case of traditional absolute point positioning approach that became widespread after the establishment of global GNSS networks with permanent stations. For a worldwide positioning in sub-meter level, an accurate determination of corrections of satellite orbits and clocks is possible using data of a global GNSS network. Data collection with a dual frequency receiver at the point, whose coordinates will be computed accurately, is enough in PPP method for determining high accurate position. So, by using code and carrier phase observations with a double frequency receiver that are utilized by the un-differenced and ionosphere-free combinations, decimeter to centimeter level point positioning accuracies may be achieved due to observation durations (^{Zumberge, 1997}; ^{Gao and Shen, 2001}; ^{Kouba and Héroux, 2001}; Gao and Shen, 2002; ^{Rizos et al., 2012}).

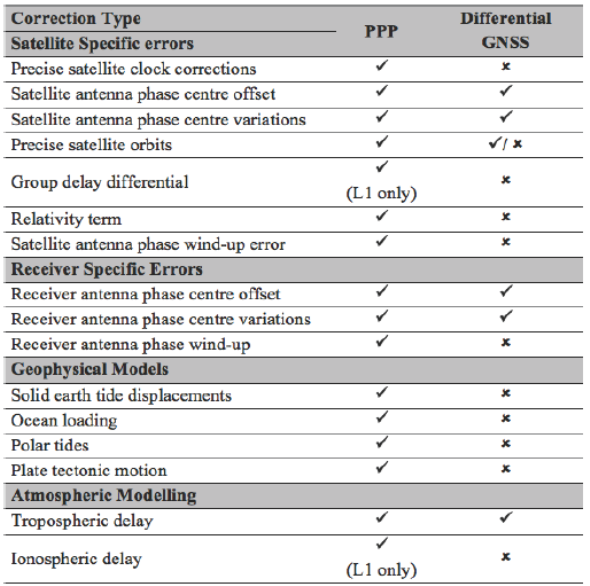
The accuracies of orbit and clock correction products and error models to be used in determination have significant importance on the point positioning accuracies to be achieved in PPP method. Therefore, considering the errors and biases separately shown in Table 3 for PPP depending on the quality of the application is the key factor to increase the position accuracy.

Table 3 Biases and errors that need to be applied for in typical PPP and differential GNSS positioning techniques (^{Rizos et al. 2012}) 

In typical PPP method, to reduce the effect of ionospheric errors, double frequency GNSS observation models (code observations and ionosphere-free carrier phase observations) have been adopted. The first effective use of the functional model in PPP has been discussed and represented in the study of ^{Zumberge et al. (1997}). ^{Kouba and Heroux (2001}), as given in Equations 2 and 3, has presented mathematical observation models of typical PPP

Here (P3) is the ionosphere-free combinations of P1 and P2 code observations, (P3)=(2.546P1-1.546P2), (L3) is the ionosphere-free combinations of L1 and L2 carrier phase observations, (L3)=(2.546 1 1.546 12 ©2), P is the geometric distance between satellite and receiver antennas in meters, C is the speed of light in meters per second, dT is the receiver clock offset according to GPS time in seconds, dt is the satellite clock offset according to GPS time in seconds, Tr is the signal delay in atmosphere (prior tropospheric delay) in meters, N carrier-phase ambiguities on L1 and L2 frequencies in cycles, respectively. , , are the carrier-phase wavelengths on L1, L2 frequencies, and combined L3 (10.7 cm) carrier phases, respectively, and P, are the components of related survey noises including multipath and un-modeled errors.

Despite the fact that traditional PPP method has had several advantages aforementioned, the most significant disadvantage of the method is to require long convergence time to solve the carrier phase integer ambiguities. To resolve an ambiguity float solution a convergence time up to 20 minutes is expected for centimeter-level positioning accuracy depending of accuracy of apriori coordinates of station and the number of received satellites, (^{Rizos et al., 2012}). Therefore, another significant factor to increase the position accuracy is the growth of the observation duration.

Since the usage percentage of PPP method is growing due to supports and GNSS products provided by several organizations such as IGS, JPL, NRCan, BKG and CODE to the users, many software algorithms for PPP in real-time and post-process have been developed (i.e. Bernese, GIPSY-OASIS, BNC, RTK-LIB, PANDA, WaPPP). In addition to this, Web-based PPP services, CSRS-PPP, GAPS, APPS, Magic-GNSS, Trimble CenterPoint RTX, etcetera, listed in Table 4, offer to the users the possibility of processing of uploaded data (^{El-Mowafy, 2011}; Ocalan and ^{Alkan, 2013}; Ocalan et al., 2013; Alkan and Ocalan, 2013; Alkan et al., 2013). Similarly, these services constantly improve to provide a user-friendly service without any fees for usage.

Table 4 Web-based services using PPP solution approach (URL-4, URL-5, URL-6, URL-7 and URL-8) 

3.1 Test Area and Control Points Characteristics

To investigate the accuracy of the relative and PPP methods by using different satellite ephemerides and software with different satellite visions around the forested areas, three test points were established at Campus of Davutpaça, Yildiz Technical University, Istanbul. Points namely; AC01, YC01 and KC01 were installed in the open area, close to the forest and within the forest area, as shown in Figure 1, respectively. The average height of the trees is approximately within 10 m-15 m in the forest area. Topcon HiperPro GNSS (GPS+GLONASS) geodetic receiver was used for collecting the data with a time span of 6 hours from 08:30 am to 02:30 pm (UTC) on the 4^th May 2015 (Day of Year: 124) at static mode. During the view, the antenna slope-heights were measured carefully minimum from two sides, and then vertical antenna heights from antenna reference point (ARP) were computed by using antenna parameters.

Figure 1 

3.2 Data Post-Processing

All data obtained from observations were converted to RINEX format and quality check of data was done by BKG Ntrip Client (BNC) v2.11.1 software. Later, GNSS data were uploaded and processed on the Web-based online services using PPP and relative approaches.

AC01 has the best satellite visibility among three points, thus the Positional Dilution of Precision (PDOP) values are better than other points' values (Fig. 2 and 3). The PDOP values and cycle slips for point YC01 are worse than the PDOP values for AC01 (Fig. 2 and 4). The worst PDOP values and satellite visibility are belonged to the point KC01 (Fig. 2 and 5). Here, improvement of the satellite visibility spatial geometry brings the PDOP values are decreased. In Figure 4, the cycle slips in satellite visibility is seen in south-west direction for YC01 where the forest area (with approximately 10 m-15 m tree heights) are placed. Moreover, as seen in Figure 5, for KC01 that has the limited satellite visibility, the satellite visibility is only traced in north-west direction limitedly.

Figure 2 PDOP plots for points AC01,YC01, KC01 

Figure 3 Analysis sky plots of point AC01 

Figure 4 Analysis sky plots of point YC01 

Figure 5 Analysis sky plots of point KC01 

Scientific software and Web-based online services were used in data processing and analyzing stages. For manual solutions, Bernese v5.2 and GIPSY-OASIS v6.3 scientific software were used by applying relative positioning approach and PPP method, respectively. For Web-based data processing, AUSPOS, OPUS (relative technique), CSRS-PPP, APPS, GAPS and Trimble-RTX (PPP Technique) were preferred. In Table 5, a brief description has been given according to used GNSS satellite ephemerides for all computations of post processing Web-based online services and manual solutions.

Table 5 Types of GNSS satellite ephemerides used in post processing 

The data processing strategy of the GAPS v5.5.0 was applied to solve the GPS observations by using ultra-rapid and rapid orbit datasets. During the analyzing process, the updated version of GAPS v5.9.0 has been presented to the users, thus data were processed according to the final orbit datasets with updated version.

Datasets were uploaded to the Web-based online services within 17 hours for ultra-rapid solutions, within 3 days for rapid solutions and approximately 14 days later for final solutions. To compare the solutions, the outcomes of the relative solution is considered as reference coordinates of stations (target coordinates) computed by Bernese v5.2 software using final orbit products. Stations BUCU, CRAO, ANKR, SOFI and NICO, involved in IGS global network, were settled as datum stations for Bernese v5.2 solutions.

Here, all computed coordinates were based on the IGS realization of ITRF 2008 reference frame at observation epoch. In the evaluation process, the offsets and correction values for the antenna phase variations of the antenna types available from the US National Geodetic Survey were used. In the first processing step, single point positioning has been performed by using ionosphere-free (L3) observable, the receiver clock errors have been eliminated, and then baselines in the network have been pre-determined. Cycle slips and outliers have been checked by using triple differences. After this process, the outliers have been removed. Later, ambiguity parameters have been solved. In order to solve the ambiguity parameters, Quasi Ionosphere Free (QIF) strategy has been applied. Consequently, precise Cartesian coordinates (X,Y,Z) of the points in ITRF 2008 reference frame at related observation epoch have been computed. We processed our GPS data using GIPSY-OASIS v6.3. It is an automated, fast, ultra-precise high precision GPS data processing software package for PPP rather than relative positioning (^{Zumberge et al., 1997}).

All of the Cartesian coordinates (X,Y,Z) provided by the systems and determined manually in ITRF2008 datum were then converted to the local topocentric coordinates (north, east and up) and differences for all components were calculated as reads by Equation 4.

Difference () = Solution - Reference Bernese v5.2 solution (4)

3.3 Results and Analysis

The point AC01 was established on the area with free satellite visibility. Coordinate differences of AC01 estimated by using different orbit products for north (n), east (e), up (u) directions and their standard deviations are listed in Tables 6 and 7 and illustrated in Figures 6, 7 and 8, respectively. The horizontal-axis shows the solution methods and vertical-axis corresponds the coordinate differences and standard deviations derived by mentioned orbit ephemerides. The solutions estimated manually by scientific software indicate that the differences computed with Bernese v5.2 using ultra-rapid and rapid orbit products are less than 1 mm in all coordinate directions. This proves the good quality of both orbit products. In contrary to this, the results obtained by GIPSY-OASIS v6.3 software are in the range of 1 and 4 mm for n and e directions and the difference amounts to maximum 8.6 mm for u direction of coordinates. These differences to the outcomes of the Bernese v.5.2 mainly accumulate due to the different modelling and default values for the signal delay in the troposphere. When the results mentioned above compare to their standard deviations, only the coordinate differences of u component for rapid ephemerides are greater than the standard deviations. Moreover, an increase has been occurred on coordinate differences when comparing the solutions of ultra-rapid orbit product and rapid orbit product. Then, a decrease has been determined when comparing the results between rapid orbit solution and final orbit solution. These differences have been in limits of their standard deviation values.

Table 6 Coordinate differences for point AC01 

Table 7 Standard deviations of the coordinate differences for point AC0 

Figure 6 Coordinate difference and standard deviation of point AC01 for n direction 

Figure 7 Coordinate difference and standard deviation of point AC01 for e direction 

Figure 8 Coordinate difference and standard deviation of point AC01 for u direction 

When the results of Web-based service for the AC01 point are analyzed, it is found that relative methods give better solution than PPP method. The maximum difference between n and e directions for AUSPOS is determined as 2.0 mm. On the u direction, the difference is increased to 12.7 mm. In AUSPOS system, a decrease has been occurred on coordinate differences, when comparing with ultra-rapid orbit solution, rapid orbit solution and final orbit solution, respectively. When the OPUS system has been analyzed, maximum 17.1 mm difference has been determined on n and e directions. All values are lower than standard deviation values. In spite of this, differences on u direction are greater and all of these values are bigger than their standard deviations. According to the results, it is determined that coordinate differences obtained from ultra-rapid orbit products in OPUS system are closer to the reference coordinates.

When web-based PPP service solutions have been examined for AC01 point, it is seen that maximum difference on n and e directions is as 13.2 mm for CSRS-PPP, APPS and Trimble-RTX services. Among them, especially APPS service has the lowest differences. For u direction, all of the service solutions except Trimble-RTX give the highest difference. Trimble-RTX service gives approximately similar solutions for all type orbit products. However, although GAPS service provides worse results for ultra-rapid and rapid orbit products, it produces better solutions especially for u direction than the other services while using final orbit products.

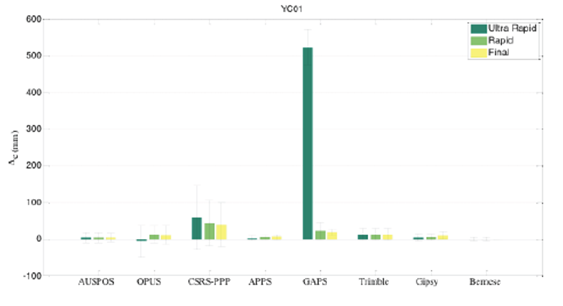
The point, namely YC01 was selected on the relatively forest area. The observation duration was 6 hours. Coordinate differences of n, e, u directions determined by using different orbit products and standard deviations are presented in Tables 8 and 9, respectively. Moreover, the graphical representation of coordinate differences and standard deviations are given in Figures 9, 10 and 11 for point YC01.

Table 8 Coordinate differences for point YC01 

Table 9 Standard deviations of the coordinate differences for point YC01 

Figure 9 Coordinate difference and standard deviation of point YC01 for n Direction 

Figure 10 Coordinate difference and standard deviation of point YC01 for e direction 

Figure 11 Coordinate difference and standard deviation of point YC01 for u direction 

When the statistical results of YC01 point have been examined, it is seen that the standard deviations have been increased due to the decrease of satellite vision. When the results of web-based services have been examined, it is seen that there is a deviation from reference coordinates on u direction, especially when comparing with ultra-rapid and rapid orbit products. At online services, there is progress on results when comparing with ultra-rapid orbit products and final orbit products. When considering the coordinate differences of n and e directions and standard deviations of them, the best results have been provided by APPS service. Moreover, if n, e and u directions have been considered together, Trimble-RTX service provides the best results.

As seen in Figure 10, GAPS service solutions for ultra-rapid ephemerides provide the worst solutions. Moreover, CSRS-PPP and GAPS services solutions for u direction provide great coordinate differences.

Table 10 Coordinate differences for point KC01 

The point, namely KC01 was selected under the forested area. The observation duration is 6 hours. Coordinate differences of n, e, u directions determined by using different orbit and standard deviations are given in Tables 10 and 11, respectively. Moreover, the graphical representation of coordinate differences and standard deviations are given in Figures 12, 13 and 14 for point KC01.

Table 11 Standard deviations of the coordinate differences for point KC01 

Figure 12 Coordinate difference and standard deviation of point KC01 for n direction 

Figure 13 Coordinate difference and standard deviation of point KC01 for e direction 

Figure 14 Coordinate difference and standard deviation of point KC01 for u direction 

The KC01 point has the worst satellite vision among the points. Problems on solving the carrier phase integer ambiguity were occurred during the analyses. Trimble-RTX could not produce any solution on point KC01. The most appropriate results for ultra-rapid and rapid orbit solutions were achieved by Bernese v5.2 scientific software.

When the differences and standard deviations of them determined from web-based services have been examined, it is found that the deviations are greater than the results of services, which use relative model. Results obtained from APPS and CSRS-PPP services among the other web-based services give efficient solutions.

As seen in Figures 12, 13 and 14, the GAPS service for ultra-rapid ephemerides provides the worst solutions among the web-based online PPP services. In addition, OPUS service solutions for all directions provide great coordinate differences among the web-based online relative services.

4. Conclusions and Recommendations

Satellite vision in GNSS survey has a significant importance for the accuracy of the estimated coordinates. This constraint has been encountered especially in surveys performed near the forested area. Moreover, accuracy of the products used in studies affects the expected results. After the survey stage, due to the determination process, one of the products, ultra-rapid, rapid or final orbit products can be used. Today, besides commercial and scientific software, web based positioning services have been used for analyzing GPS/GNSS data, which are free. Due the development and common use of these services, PPP method for next generation positioning has come to the forefront.

In this study, the accuracy of PPP method versus relative method has been investigated according to the different satellite orbit products where satellite vision is limited. For this purpose, analyses have been performed with six different Web-based services, then performances of them have been compared. For manual solutions, the estimation was achieved by Bernese v5.2 and GIPSY-OASIS v6.3 scientific software. Post processing solutions for CSRS-PPP and Trimble-RTX Web-based online services use GPS+GLONASS observations. However, the other Web-based online services and manual solutions in post processing use GPS only observations. In survey areas, where the satellite visibility is limited such as forest regions as illustrated in this study, the use of GPS+GLONASS observations in post processing could be an advantage due to the increase of number of observations. But, this is not the unique parameter to improve the point positioning accuracy in post processing solutions.

The analyses of outcomes show that Web-based services (except GAPS and Trimble-RTX) and manual solutions used in this study estimate accuracy of coordinate components of north and east as approximately 1 cm level (in all cases when ultra-rapid, rapid and final satellite orbit products were used) for the station with free satellite visibility (AC01). For AC01, considering the ephemerides used in post processing solutions, the significant improvement on coordinate components are provided by GAPS service in respect to use of ultra-rapid, rapid and final products.

For the point YC01 located near the forest area where the satellite vision decreases or partially disturbed, the positioning accuracy decreases. Here, manual solutions processed by scientific software (Bernese and GIPSY-OASIS) give the best results. Among the Web-based online services applying relative model approach, AUSPOS offers the best solution for partially prevention of satellite signals. Furthermore, the PPP-solution of the Trimble-RTX delivers a better positioning accuracy than the outcomes of the other Web-based services using PPP approach for YC01.

This outcome for YC01 estimated by Trimble-RTX, using PPP solution and its own satellite ephemerides products could be related to use of multi constellation of GNSS in the areas with limited satellite visibility because of increasing of the number of measurements.

In contrary to this, Trimble-RTX could not produce any solution for point KC01 (vastly prevention of satellite signals). Here, the best solution was provided by APPS service using PPP approach. Among the Web-based online services applying relative model approach, AUSPOS offers the best solution for KC01.

Consequently, using scientific software manually on the analyses provides advantages to the users to achieve high accuracy on results in all conditions. The fundamental reason of it is that the user has an option to interfere the estimation and analyzes stages during the process. In spite of this, the professional use of scientific software requires a long-term experience. However, web-based services represent basic internet based interface, which users of all level may easily use. They produce fast and easy solutions for post-processing stage at positioning applications.

However, several factors affect the positioning accuracy under the different satellite visibilities. These factors can be listed as; used satellite observations (GPS only, GPS+GLONASS etc.), the solution algorithms (relative or PPP), satellite ephemerides product types (ultra-rapid, rapid and final) and the other correction models, that the users should take into consideration of them.