English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introduction
Earthquake surface wave tomography has become a powerful tool to image the deep structures of the crust and upper mantle due to its dispersion characteristics. Measuring high-quality group velocities or phase velocities of surface wave, such as Rayleigh wave, is a key foundation for surface wave tomography. Currently, there are some methods to measure group velocities of surface wave, such as Moving Window Analysis (MWA) (Landisman et al., 1969), Multiple Filter Technique (MFT) (Dziewonski et al., 1969) and Continuous Wavelet Transform (CWT) (Jiang et al., 2017), of which MFT is the most commonly used one (Ritzwoller & Levshin, 1998; Zhu et al., 2002; Huang et al., 2003; Cho et al., 2007; Li et al., 2009; Saygin & Kennet, 2010; Rindraharisaona et al., 2017; Tang et al., 2018; Lu et al., 2018; Mechie et al., 2019).
In 1969, MWA was proposed by Landisman et al. using rectangular window in time domain. In the same year, MFT was presented by Dziewonski et al. using Gaussian filter in frequency domain. When taking Gaussian filter instead of rectangular window in time domain, MWA is equivalent to MFT in frequency domain. MFT, a commonly used method, is dominantly dependent on the value of Gaussian filter parameter a, and much research has been done (Inston et al., 1971; Cara, 1973; Nyman & Landisman, 1977; Herrmann & Ammon, 2004; Kolinsky, 2004; Zhu et al., 2007; Chen et al., 2014; Jiang et al., 2019). Especially, Herrmann and Ammon (2004) gave recommended values of Gaussian filter parameter a with distance variation when the period is from 4 s to100 s. CWT was used to measure group velocities of earthquake Rayleigh wave, compared to MFT (Jiang et al., 2017).
In 1996, S transform was proposed by Stockwell et al., which is an extension of CWT based on Morlet wavelet (Stockwell et al.,1996). S-transform combines advantages of short-time Fourier transform (STFT) and wavelet transform (WT). For instance, inverse S transform is directly related to Fourier transform and it is a lossless transformation, linear transformation has no cross-term and high time-frequency resolution, the time-frequency resolution is related to the frequency of the signal, and the basic wavelet need not satisfy the admissibility condition (Pinnegar & Mansinha, 2003a, 2003b; Zheng & Wang, 2015). In recent years, S-transform has been widely used in geophysics (Pinnegar & Eaton, 2003, 2006; Askari & Siahkoohi, 2008; Parolai, 2009; Askari et al., 2011; Tselentis et al., 2012; Askari & Ferguson, 2012; Tu et al., 2013; Zheng & Wang, 2015). In this paper, S transform is introduced to measure group velocities of earthquake Rayleigh wave and is compared with the commonly used MFT.
S transform
If x(t) is a surface wave signal generated by natural earthquake, then the S transform of x(t) is defined as
where t is time, t is the central point of the window function and can control the position of window function along time axis, and f is frequency. In S transform, Gaussian function and basic wavelet are respectively defined as
The basic wavelet in S-transform is the product of simple harmonics only scaled in time domain and Gauss function scaled and shifted. Time window width of S-transform varies inversely with frequency, i.e. the time window is wider in low frequency band, which leads to higher frequency resolution, while the time window in high frequency band is narrower, which leads to higher time resolution. Therefore S transform is self-adaptive.
Inverse S transform is written as
Comparison with MFT
At present, MFT is the most commonly used method to measure group velocities of earthquake Rayleigh wave. Based upon the synthetic Rayleigh wave at different epicentral distances and real earthquake Rayleigh wave, S transform is compared with MFT.
MFT
Choosing appropriate value of Gauss filter parameter α can reduce the group-velocity measurement error of surface wave. The recommended values of α with epicentral distance variation in the period range from 4 s to 100 s given by Herrmann and Ammon (2004) are listed in Table 1, in which the value of α at epicentral distance of 3 000 km is originally not available but is obtained by interpolation of the values at epicenter distances of 2 000 km and 4 000 km.
Synthetic Rayleigh waves
In order to check the effectivity of S transform in the measurement of group velocities and compare S transform with MFT, synthetic data of Rayleigh waves were generated by modal summation method (Herrmann & Ammon, 2004) based upon AK135 earth model (Kennett et al., 1995), and the source parameters are listed in Table 2. There are five stations with epicentral distances of 1 000 km, 2 000 km, 3 000 km, 4 000 km and 8 000 km, respectively. The azimuth angles of such stations are 45° and the sampling interval of data is 1 s. Synthetic seismogram of Rayleigh wave at epicentral distance of 3000 km and its amplitude spectra are shown in Figure 1.
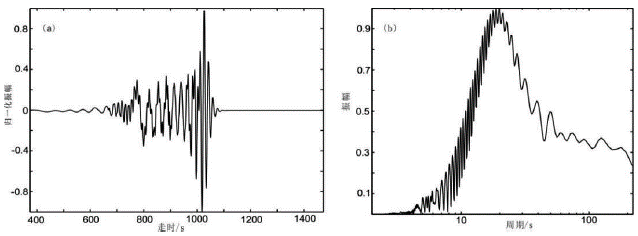
Figure 1 Synthetic seismogram of Rayleigh wave at distance of 3000 km (a) and its amplitude spectra (b)
And then S transform and MFT are respectively applied to measure group velocities of the synthetic data . From the results by such two methods (Fig. 2), the following conclusions can be drawn:
1) when the epicentral distance is 1 000 km, the accuracy of group-velocity curve obtained by S-transform is slightly lower than that by MFT in the period range of less than or equal to 15 s but much higher in the other period range, in the period range of greater than 40 s group-velocity curves measured by S transform and MFT both have large error and therefore the period to be measured should not be large when the epicentral distance is small;
2) when the epicentral distance is 2 000 km, 3 000 km or 4 000 km, the accuracy of group-velocity curve obtained by S-transform is similar as that by MFT in the period range of less than or equal to 15 s but much higher in the other period range, especially when the period is greater than 40 s the group-velocity curve obtained by MFT fluctuates obviously and has large error with the theoretical one while that by S transform fits well with the theoretical one;
3) when the epicentral distance is 8 000 km, the accuracy of group-velocity curve obtained by S-transform is lower than that by MFT in the period range of less than or equal to 15 s but higher in the other period range. On the whole, the group-velocity curve gained by S transform fits better with the theoretical one than MFT, therefore its accuracy is higher than that of MFT.
Real earthquake Rayleigh wave
The real seismogram of earthquake Rayleigh wave acquired from mobile station in Guangxi of China is shown in Fig. 3 and the parameters of the earthquake event are listed in Table 3. The coordinates of the station are (110.50°E, 24.09°N) and epicentral distance is 3 551.22 km. For MFT, the value of Gauss filter parameter a at such epicentral distance is 87.5 by interpolation (Table 1).
Then S transform and MFT are respectively applied to measure group velocities of such real data and the results are shown in Fig.4. Overall the group-velocity curves obtained by S transform and MFT are similar. But when the period is greater than 40 s, the group-velocity curve obtained by MFT fluctuates obviously while the curve by S transform is much smoother, hence S transform is more reliable than MFT.
Conclusions
In this paper, based upon the synthetic Rayleigh wave at different epicentral distances and real earthquake Rayleigh wave, the group velocities are measured by CWT and MFT respectively. From the analysis and comparison, the conclusions can be drawn generally as following:
1) when the epicentral distance is small, such as 1 000 km, in the period range of greater than 40 s group velocities measured by S transform and MFT both have large error and are both not reliable and therefore the period to be measured should not be large in such case;
2) when the period is greater than 15 s, S transform has higher accuracy than MFT at all epicenter distances, especially when the period is greater than 40 s the group-velocity curve obtained by MFT fluctuates obviously and its accuracy is much lower than that by S transform;
3) when the period is less than or equal to 15 s, the accuracy of S transform is lower than that of MFT at epicental distances of 1000 km and 8000 km (especially 8000 km), and the accuracy of such two method is similar at the other epicental distances.
On the whole, S transform is more accurate than MFT. Furthermore, MFT is dominantly dependent on the value of the Gaussian filter parameter a, but S transform is self-adaptive. Therefore, S transform is a more stable and accurate method than MFT for group velocity measurement of earthquake Rayleigh waves.
