Introduction
The use of Global Navigation Satellite Systems (GNSS) in engineering and scientific studies has increased considerably along with recent developing technology. With this technology, accurate Cartesian (X, Y, Z) or geodetic (φ, λ, h) coordinate information for any point on the Earth is easily available (Seeber, 2003). However, the GNSS-derived ellipsoidal height is not used directly in engineering studies. In order to use ellipsoidal heights obtained from GNSS data with orthometric heights obtained from geometric leveling measurements, geoid undulations must be determined accurately. The relationship between the ellipsoidal and orthometric heights of any point on earth can be calculated by using Equation (1) (Heiskanen & Moritz, 1967).
where N refers to geoid undulation, h is the ellipsoidal height, and H is the orthometric height.
Two different methods are used in geoid modeling: gravimetric and geometric (Featherstone et al., 1998; Kotsakis & Sideris, 1999). With the geometric approach, many different techniques such as interpolation and least-squares collocation (LSC) methods are used to determine a local geoid (Zhong, 1997; Zhan-ji & Yong-qi, 1999; Yanalak & Baykal, 2001; Erol & Çelik, 2004; Zaletnyik et al., 2004; Erol et al., 2008; Tusat, 2011; Rabah & Kaloop, 2013; Doganalp, 2016; Das et al., 2018; Ligas & Kulczycki, 2018; Tusat & Mikailsoy, 2018; Dawod & Abdel-Aziz, 2020). For example, Doganalp & Selvi (2015), using GNSS/leveling data (40 reference points and 205 test points), determined a geoid of the 57-km-long Nurdagi-Gaziantep highway project. Polynomial, LSC, multiquadric (MQ), and thin plate splines (TPS) methods were used for geoid undulation calculation. The findings determined that using polynomial methods with LSC had a positive effect on the results in strip projects. It was concluded that MQ and TPS prediction methods along with the LSC method performed better than polynomial methods in calculations for strip projects. They also commented that if the number of reference points had been increased, the results might have been better. Karaaslan et al. (2016) created a local geoid model in Trabzon Province using geometric methods. Polynomial surfaces were created using MQ and weighted average (WA) interpolation methods. In the study, a 600-point dataset was divided into reference and test data by looking at point distributions and orthometric height values. As a result of the study, the best geoid model was obtained with a non-perpendicular third-degree polynomial surface.
With the development of computer technology, studies in the field of artificial intelligence (AI) have accelerated and various solution methods have been developed for different problem types. Studies have shown that application of AI methods in the field of geodesy has been increasing in recent years and that they have proven to be quite useful to researchers working in the field, especially in the formulating of predictions using fuzzy logic as an alternative to classic methods (Yilmaz & Arslan, 2008; Yilmaz, 2010; Tusat, 2011; Erol & Erol, 2012; Erol & Erol, 2013). One type of AI technology is the artificial neural network (ANN). The ANN produces successful results under conditions of multivariable and complex mutual interaction between variables or when there is no single solution set. With these features, ANN is seen as a suitable method for geoid undulation determination. Studies have yielded successful results by using ANN (Stopar et al., 2006; Lin, 2007; Akyilmaz et al., 2009; Pikridas et al., 2011; Veronez et al., 2011; Akcin & Celik, 2013; Erol & Erol, 2013; Elshambaky, 2018; Kaloop et al., 2018; Albayrak et. al, 2020; Erol & Erol, 2021). For example, Seager et al. (1999) performed local geoid modeling using a feedback artificial neural network (FBANN) to determine the geoid. The results demonstrated that the ANN could be used as a tool in geoid determination and that it gave rapid results. Kavzoglu & Saka (2005) performed a local geoid undulation calculation for Istanbul using an ANN with GPS/leveling data. The ANN results were compared with the polynomial and LSC methods. The results produced by the ANN were just as accurate as the two classic methods. Cakir & Yilmaz (2014) determined a local geoid using polynomial, MQ, radial basis function (RBF), and multi-layer perceptron neural network (MLPNN) methods in Kayseri Province and compared their performances. Compared to the RBF, the MQ was more successful, whereas the MLPNN yielded better results than all the other methods. In addition to the methods mentioned above, regression methods have also been used in geoid undulation determination (Konakoglu & Akar, 2021). For example, Kaloop et al. (2020) examined the usability of multivariate adaptive regression splines (MARS), Gaussian process regression (GPR), and kernel ridge regression (KRR) methods in geoid undulation modeling using GPS/leveling observations. The results obtained with these methods were compared with the results of the LS-SVM. According to the statistical tests, the KRR yielded better results than the other methods.
One of the factors affecting the accuracy of a geoid model is how correctly it is represented by the selected training set used to create it. The geoid undulation determination studies given above show that a dataset is divided into two parts as training and testing data according to the spatial homogeneity distribution criteria. Studies are conducted in this way to determine the performance of the method. The model is trained with the training dataset before the prediction is made. The correctness of the trained model is statistically determined using the testing dataset. Thus, whether or not to use the established model can be decided. In this study, the k-fold cross validation was applied for the first time in a local geoid determination study, with the aim of minimizing deviations and errors caused by distribution and division.
The main aim of this study was to provide a comprehensive comparative analysis of different approaches for the prediction of the geoid undulation. The methods examined consisted of two soft computing techniques (RBFNN and GRNN) and eleven conventional methods including: 1) multiple linear regression (MLR), 2) kriging (krig), 3) inverse distance to a power (IDP), 4) triangulation with linear interpolation (TLI), 5) minimum curvature surface (MCS), 6) natural neighbor (NN), 7) nearest neighbor (NRN), 8) local polynomial (LP), 9) radial basis function (RBF), 10) polynomial regression (PR), and 11) modified Shepard's (MS). The performance of the methods was evaluated using the root mean squared error (RMSE), mean absolute error (MAE), the Nash-Sutcliffe efficiency (NSE) coefficient, and the coefficient of determination (R2). This is the first study to provide a comprehensive comparison of thirteen methods used in the prediction of geoid undulation and it is expected that scientists interested in geoid computations may benefit from its findings.
Material and Methods
Study area and dataset
The study area of approximately 4664 km2 is between the 40° 30' and 41° 0' latitudes and 39° 0' and 40° 30' longitudes within the borders of the province of Trabzon. Figure 1 shows the location of the study area. The topography is irregular, with orthometric height varying between 22.87 and 3387.14 m and geoid undulations between 24.6 and 30.7 m. (Karaaslan et al. (2016). For this application, 537 C2 (second order densification) and C3 (third order densification) points covering the entire area of Trabzon obtained from the Trabzon IX Regional Directorate of the Turkish Land Registry and Cadastre were used. The latitude (φ), longitude (λ), ellipsoidal height (h) and orthometric height (H) values of each point are known. The orthometric heights (H) of the points were obtained via the geometric leveling method and the ellipsoidal heights (h) via GPS/GNSS static measurement. The spatial density of the points (1 point per 9 km2) demonstrated a good characterization of the topography. The input parameters, comprised of the latitude (φ) and longitude (λ) values, were used to develop the ANN models. The geoid undulation value (N) served as the output parameter.
The k-fold cross validation method was used to balance the features in the dataset used in the study and to accurately measure the performance of the method in the unbalanced datasets. The value of the k parameter required for cross-correcting was determined as 5. Thus, the dataset was divided into five parts, with four used for training and the other one used to test the algorithm. To perform the cross-validation, the dataset was divided into approximately 80% for training sets (reference points) and 20% for testing sets (test points). Table 1 indicates the statistical properties of the geodetic data used in this study, including the mean, minimum, maximum, standard deviation, and skewness values of these five different datasets (DS#1, DS#2, DS#3, DS#4, and DS#5).
The corresponding average latitude and longitude values were determined as 40.73950° (40.47765° - 40.97722°) and 40.06419° (39.30994° - 40.49945°). Negative distortion was determined in the latitude, longitude, and geoid undulation dataset values. The distribution of negative distortion was indicated with an asymmetrical tail extending toward the more negative (lower than average) values. This showed that the skewness values were generally close to zero, and in this case, that the data were in normal distribution. The statistical parameters given in Table 1 show that there were no significant differences among the datasets created. The geographical distribution of the five different datasets (DS#1, DS#2, DS#3, DS#4 and DS#5) is shown in Figure 2.
Table 1 Statistical parameters of the geodetic data (latitude, longitude, and geoid undulation) used in the study
| Dataset | Phase | Statistical characteristics | φ (°) | λ (°) | N (m) |
|---|---|---|---|---|---|
| DS#1 | Training | Mean | 40.739 | 40.059 | 28.418 |
| Minimum | 40.478 | 39.340 | 24.661 | ||
| Maximum | 40.969 | 40.499 | 30.748 | ||
| Standard deviation | 0.110 | 0.294 | 1.439 | ||
| Skewness | -0.144 | -0.663 | -0.644 | ||
| Testing | Mean | 40.743 | 40.085 | 28.327 | |
| Minimum | 40.491 | 39.310 | 24.597 | ||
| Maximum | 40.977 | 40.492 | 30.673 | ||
| Standard deviation | 0.108 | 0,28524 | 1.372 | ||
| Skewness | -0.259 | -0,79471 | -0.503 | ||
| DS#2 | Training | Mean | 40.741 | 40.072 | 28.357 |
| Minimum | 40.478 | 39.329 | 24.597 | ||
| Maximum | 40.977 | 40.499 | 30.748 | ||
| Standard deviation | 0.110 | 0.290 | 1.431 | ||
| Skewness | -0.194 | -0.744 | -0.590 | ||
| Testing | Mean | 40.733 | 40.032 | 28.571 | |
| Minimum | 40.519 | 39.310 | 24.661 | ||
| Maximum | 40.969 | 40.492 | 30.689 | ||
| Standard deviation | 0.109 | 0.301 | 1.396 | ||
| Skewness | -0.052 | -0.477 | -0.731 | ||
| DS#3 | Training | Mean | 40.737 | 40.073 | 28.419 |
| Minimum | 40.478 | 39.310 | 24.597 | ||
| Maximum | 40.977 | 40.499 | 30.748 | ||
| Standard deviation | 0.110 | 0.290 | 1.424 | ||
| Skewness | -0.188 | -0.722 | -0.600 | ||
| Testing | Mean | 40.752 | 40.030 | 28.323 | |
| Minimum | 40.520 | 39.329 | 24.661 | ||
| Maximum | 40.969 | 40.466 | 30.692 | ||
| Standard deviation | 0.106 | 0.300 | 1.433 | ||
| Skewness | -0.042 | -0.561 | -0.684 | ||
| DS#4 | Training | Mean | 40.739 | 40.062 | 28.409 |
| Minimum | 40.478 | 39.310 | 24.597 | ||
| Maximum | 40.977 | 40.492 | 30.748 | ||
| Standard deviation | 0.110 | 0.294 | 1.435 | ||
| Skewness | -0.133 | -0.685 | -0.628 | ||
| Testing | Mean | 40.741 | 40.075 | 28.362 | |
| Minimum | 40.509 | 39.365 | 25.331 | ||
| Maximum | 40.919 | 40.499 | 30.658 | ||
| Standard deviation | 0.109 | 0.283 | 1.393 | ||
| Skewness | -0.303 | -0.697 | -0.566 | ||
| DS#5 | Training | Mean | 40.740 | 40.065 | 28.384 |
| Minimum | 40.478 | 39.329 | 24.661 | ||
| Maximum | 40.969 | 40.499 | 30.748 | ||
| Standard deviation | 0.109 | 0.289 | 1.429 | ||
| Skewness | -0.187 | -0.712 | -0.579 | ||
| Testing | Mean | 40.738 | 40.061 | 28.461 | |
| Minimum | 40.491 | 39.310 | 24.597 | ||
| Maximum | 40.977 | 40.492 | 30.325 | ||
| Standard deviation | 0.112 | 0.304 | 1.414 | ||
| Skewness | -0.085 | -0.605 | -0.774 |
Figure 2 Geographical distribution of the reference and test points of the 5 different datasets: (a) DS#1, (b) DS#2, (c) DS#3, (d) DS#4, (e) DS#5
Data normalization is a pre-processing stage that plays a significant role in the performance of ANN methods. In order to obtain more accurate results, all data should be normalized before proceeding with the training and testing stages. Therefore, input and output parameters were normalized to the interval [-1, 1] and the normalized value (Y norm ) for each input and output parameter (Y i ) was obtained using Equation (2).
where High value and Low value are set to 1 and -1, respectively.
Artificial neural network (ANN)
The artificial neural network (ANN) was inspired by the working principle of the biological nervous system and was created by artificially simplifying and imitating the nerve cells (neurons) in the nervous system and then transferring them to a computer (Singh et al., 2009). Since ANNs are modeled after the biological nervous system, they have the advantage of being capable of automatically, on their own, realizing skills such as the ability to derive and discover new information through learning, which is one of the features of the human brain. Generalization and working with an unlimited number of variables are also features of the ANN. Supplying the learning and quick decision-making abilities of the human brain to ANNs enables them to solve complex problems through training. The ANN looks at examples of problems, makes generalizations about these problems, sums up the information, and then, when encountering new examples it has never seen before, it makes decisions using the information it has learned. Because of all these features, the ANN is used to accomplish goals in many areas, including classification, control, image processing, modeling, feature determination, optimization, prediction, and more. As there is no limit to the application fields of ANNs, they can be applied to almost any problem that can be converted into fixed input and output variables. In this study, two types of ANN (RBFNN and GRNN) were applied. The development of the models was coded in a MATLAB environment. An overview and description of all the applied methods are discussed in the following sections.
Radial basis function neural network (RBFNN)
The RBFNN was developed in 1988, inspired by the action-response behavior seen in biological nerve cells (Broomhead & Lowe, 1988). The RBFNN is a curve-fitting approach in multidimensional space and is a special version of the multi-layer artificial neural network that uses the radial basis function as its activation function. Like the general ANN architecture, the RBFNN method is defined in three layers: input layer, hidden layer, and output layer (Figure 3).
The input layer of the network is directly connected to the hidden layer and subsequently, weights are only present between the hidden layer and the output layer. The RBFNN has a single hidden layer and radial basis functions are used as the activation function in the hidden layer neurons. The most commonly used radial basis function is the Gaussian function (Hartman et al., 1990; Park & Sandberg, 1991). The output of an RBFNN with Gaussian-based function can be calculated using the following equations (Haykin, 1994).
where is the input vector, c i is the center of the RBF unit, is the width of the neuron, n is the number of cells in the hidden layer, and w i shows the link weights between the hidden and output layers. A different number of hidden layer neurons and spread parameters were investigated using the RMSE.
General regression neural network (GRNN)
The GRNN proposed by Specht (1993) does not require an iterative procedure as in the MLPNN method. It needs only one-way learning. Due to the simplicity of the network structure and ease of implementation, this functional approach has been used in different geodetic applications (Ziggah et al., 2017; Cakir & Konakoglu, 2019; Li et al., 2020). The GRNN consists of four layers: the input layer, the pattern layer, the summation layer, and the output layer (Specht, 1993). The structure of the GRNN is given in Figure 4.
The input layer, i.e., the first layer where inputs are given, depends on the following pattern layer. The distances between training data and testing data are calculated in this layer. The results are passed through the radial basis function together with the selected value to obtain the weight values. These weight values are transferred to the numerator and denominator neurons in the summation layer. In the numerator neuron, the output value of the training data whose weight values are in the neuron is multiplied and the multiplication values are summed up. In the denominator neuron, weights are summed up directly. The output value is obtained by dividing the numerator value by the denominator value in the output layer, as shown in Equation (6).
where n is the number of data, s is the spread parameter, and D 2 represents the scalar function, as shown in Equation (7).
In this method, having only the spread parameter (σ), there are not as many main design parameters as with the MLPNN (e.g., number of hidden layers, number of neurons in each hidden layer, activation function, and training type). The only important parameter that has to be determined using this method is the spread parameter (σ). There is no specific rule about how this parameter is selected. In this study, different spread parameters between 0 and 1 were tested using the minimum RMSE criterion.
Multiple linear regression (MLR)
In regression methods, the influencing variables are called explanatory variables (independent variables), and the affected variable is called the described variable (dependent variable). The MLR method reveals the cause-effect relationship between the dependent variable (Y) and independent variables (x 1 , x 2 ,..., x n ) as a mathematical model which can be written as Equation (8) (Çahin et al! 2013).
where a 0 , a 1 , a 2 , …, a n show the effect of each independent variable on the dependent variable.
Interpolation methods
Interpolation is the prediction of the dimensions of unmeasured points using measured values of sample reference points. In this study, Surfer software v. 17 was used for interpolation calculation (Golden Software, 2019). The software turns both simple and complex data into understandable visual tools such as maps, charts, and models. The Surfer software v. 17 offers users the opportunity to determine a geoid using 12 different interpolation methods. Of these 12 interpolation methods, those used for this study included the kriging (krig), inverse distance to a power (IDP), triangulation with linear interpolation (TLI), minimum curvature surface (MCS), natural neighbor (NN), nearest neighbor (NRN), local polynomial (LP), radial basis function (RBF), polynomial regression (PR), and modified Shepard's (MS). Detailed information about these ten methods can be found in the work of Keckler (1995).
A-fold cross-validation method
In classic and AI applications, datasets are divided into those for the training and those for the testing of the established model. This separation method is carried out in several ways. The hold-out method is widely used to provide generalization. In classic and AI methods, the sampling methodology used for data division can have a significant impact on the quality of the subsets used for training and testing. The k-fold cross-validation method is one of the methods used in data partition. In this validation method, the dataset to be used in the prediction is randomly divided into a k number of parts. The testing datasets consist of parts created in the order of each separate training part (k 1 ...). In this way, every part that is created up to k is used as a testing set. The accuracy of the method is determined by taking the average of the accuracy values obtained from each part (Stone, 1974; Kohavi, 1995; Rodríguez et al., 2009). In this study, the value of k was taken as 5 (Figure 5).
In Figure 5, the dataset is divided into five equal parts. The green parts represent the training data and the orange parts the testing data. In other words, when four parts of five datasets are used for training, one part (the fifth) is used for testing. In this way, modeling was performed five times, using each part once for testing and the other four parts for training. The arithmetic averages of the success rates were calculated for the five models and the resulting success rate was determined. Ziggah et al. (2019) demonstrated the potential and feasibility of using the k-fold cross-validation method on coordinate transformation from geodetic applications. The dataset for a Ghana geodetic reference network was divided into separate training and testing data according to the hold-out method. The findings revealed that false results could be generated, and it was shown that the use of the k-fold cross-validation method provided a better solution for the correct evaluation of method performance, especially in the case of a sparse dataset.
Performance Evaluation Criteria
To measure the prediction success of the developed models, this study used the root mean square error (RMSE), mean absolute error (MAE), Nash-Sutcliffe efficiency (NSE) coefficient, and the coefficient of determination (R2). The equations used in the calculation of the selected statistical criteria are given below.
Root mean square error:
Mean absolute error:
Nash-Sutcliffe efficiency coefficient:
Coefficient of determination:
where n is the number of datasets, O i is the observed geoid undulation value, O is the mean of the observed geoid undulation values, P i is the predicted geoid undulation value, and P represents the mean of the predicted geoid undulation values.
The RMSE is used to determine the error rate between the prediction and the corresponding observation. The prediction ability of the method increases as the error value approaches zero. The MAE is used to determine the absolute error between the prediction and the corresponding observation. The closer the error value is to zero, the better the method's prediction ability is indicated. The NSE coefficient ranges from -∞ to 1. Thus, when NSE = 1, it means that the method is perfect. An NSE value of between 0 and 1 generally means that the method performance is acceptable, whereas a value of less than 0 emphasizes that the average observation value showing the performance of the method is insufficient is a better prediction than the calculated data. The R2 is an indication of whether or not the regression equation is compatible with the data. It is the ratio that explains one difference in terms of the overall difference. This ratio is called the coefficient of certainty and shows the extent to which the difference in the dependent variable can be explained by the independent variable. The R2 is expressed by a value of between 0 and 1. A value close to 1 indicates that a large part of the variance in the dependent variable explains the independent variable in the method.
Results and Discussion
The results of the developed models are given under separate headings. It should be noted that in the tables, the best metric values are highlighted in dark gray, whereas the worst are highlighted in light gray.
RBFNN results
The performance of the RBFNN is based on the spread parameter and the maximum number of neurons in the hidden layer. Various attempts were made to achieve the best performance using a different number of neurons and different spread parameters. The best performance criteria results obtained during the training and testing phases are given in Table 2. The optimum values for the maximum number of neurons and their spread were 430/0.025 for DS#1, 421/0.056 for DS#2, 427/0.076 for DS#3, 412/0.034 for DS#4, and 410/0.065 for DS#5.
Table 2 RBFNN training and testing phase results
| Phase | Dataset | RMSE (m) | MAE (m) | NSE |
|---|---|---|---|---|
| Training | DS#1 | 0.112 | 0.079 | 0.99383 |
| DS#2 | 0.001 | 0.000 | 0.99999 | |
| DS#3 | 0.000 | 0.000 | 0.99999 | |
| DS#4 | 0.034 | 0.009 | 0.99944 | |
| DS#5 | 0.003 | 0.001 | 0.99999 | |
| Testing | DS#1 | 0.197 | 0.115 | 0.97925 |
| DS#2 | 0.780 | 0.542 | 0.68478 | |
| DS#3 | 0.525 | 0.364 | 0.86442 | |
| DS#4 | 0.720 | 0.590 | 0.73029 | |
| DS#5 | 0.569 | 0.389 | 0.83665 |
The lowest RMSE value of the prediction models at the training stage was obtained with DS#3 and the highest with DS#1. Moreover, the lowest MAE value was also found in DS#3. According to Table 2, the highest NSE values during the training stage were with DS#2, DS#3, and DS#5. At the testing stage, the lowest RMSE value was obtained with DS#1 and the highest with DS#2, whereas the lowest MAE and the highest NSE values were determined in DS#1. During the training phase, DS#2, DS#3, DS#4, and DS#5 performed well, whereas in the testing phase, the performance results of DS#1 were better than in the others. In order to demonstrate the performance of the RBFNN, the predicted geoid undulation values and those observed at the testing stage for each dataset (DS#1, DS#2, DS#3, DS#4, and DS#5) are shown in Figure 6.
Thus, it is clear that the geoid undulation prediction made with DS#1 was superior to that of the other datasets. It is also clear that the a and b coefficients of the distribution graphs from the fit line equations (assuming that the equation was y = ax + b) were higher than the a and b coefficients obtained with the other datasets; a was close to 1 and b close to 0, and the R2 value was higher.
GRNN results
The performance of the GRNN largely depends on the spread parameter, so determining this parameter is of great importance. Therefore, in order to optimize prediction performance, this parameter must be accurately determined according to the evaluation criteria. The GRNN spread parameter values that provided the best testing performance were determined as 0.015, 0.013, 0.020, 0.022, and 0.012 for DS#1, DS#2, DS#3, DS#4, and DS#5, respectively. The prediction performance of the GRNN for the training and testing stages in terms of the RMSE, MAE, and NSE is given in Table 3.
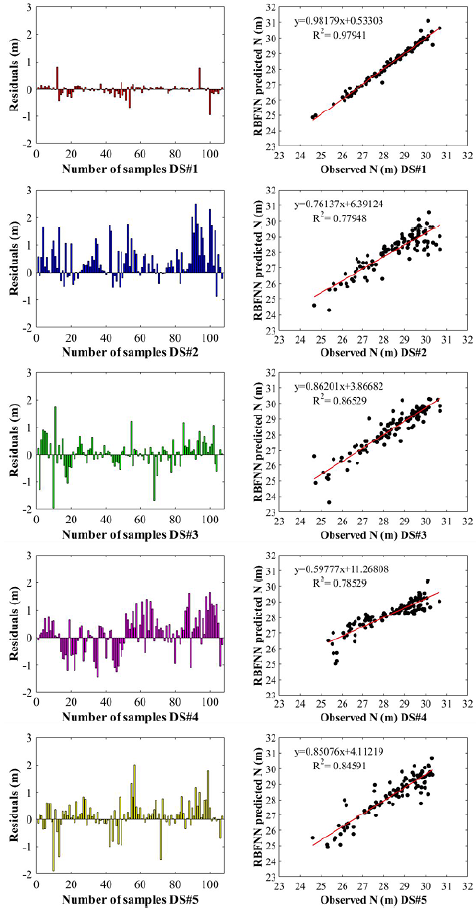
Figure 6 Comparison of the geoid undulation values predicted by RBFNN and those observed at the testing phase
According to Table 3, the lowest RMSE value in the training stage was obtained with DS#4, and the highest with DS#2. The lowest MAE value was determined with DS#4, whereas the highest NSE value at the training stage was determined again in DS#4. The lowest RMSE value in the testing phase was found with DS#4 and the highest with DS#2, whereas the lowest MAE and the highest NSE values were determined in DS#4. During the training and testing phases, the performance results of DS#4 were better than those of the others. In order to illustrate the success of the GRNN, the predicted geoid undulation values and those observed at the testing stage for each dataset (DS#1, DS#2, DS#3, DS#4, and DS#5) are shown in Figure 7.
Table 3 GRNN training and testing phase results
| Phase | Dataset | RMSE (m) | MAE (m) | NSE |
|---|---|---|---|---|
| Training | DS#1 | 0.024 | 0.007 | 0.99969 |
| DS#2 | 0.048 | 0.019 | 0.99886 | |
| DS#3 | 0.019 | 0.004 | 0.99981 | |
| DS#4 | 0.012 | 0.003 | 0.99993 | |
| DS#5 | 0.039 | 0.016 | 0.99927 | |
| Testing | DS#1 | 0.199 | 0.147 | 0.97873 |
| DS#2 | 0.201 | 0.140 | 0.97912 | |
| DS#3 | 0.173 | 0.134 | 0.98530 | |
| DS#4 | 0.167 | 0.124 | 0.98550 | |
| DS#5 | 0.187 | 0.140 | 0.98230 |
The diagrams show that the results obtained with all datasets were quite close to each other. The fact that in the equation for determining linearity (y = ax + b), coefficient a was close to 1 and coefficient b close to 0 indicated that there was a good relationship between the observed and the predicted geoid undulation values. In addition, as can be seen from Figure 7, the determination coefficient (R2) between the observed and predicted values of DS#4 during the testing phase was 0.98575.
MLR results
The results calculated according to the regression equations for geoid undulation are given below for the five different datasets.
The geoid undulation (N) was defined as the dependent variable and latitude (φ) and longitude (λ) were regarded as the independent variables. The results of the statistical evaluation criteria for the MLR geoid undulation prediction are presented in Table 4.
Table 4 MLR training and testing phase results
| Phase | Dataset | RMSE (m) | MAE (m) | NSE |
|---|---|---|---|---|
| Training | DS#1 | 0.432 | 0.346 | 0.90959 |
| DS#2 | 0.448 | 0.356 | 0.90175 | |
| DS#3 | 0.449 | 0.356 | 0.90038 | |
| DS#4 | 0.436 | 0.341 | 0.90753 | |
| DS#5 | 0.436 | 0.346 | 0.90685 | |
| Testing | DS#1 | 0.466 | 0.351 | 0.88358 |
| DS#2 | 0.402 | 0.310 | 0.91627 | |
| DS#3 | 0.397 | 0.312 | 0.92260 | |
| DS#4 | 0.557 | 0.446 | 0.83850 | |
| DS#5 | 0.455 | 0.340 | 0.89569 |
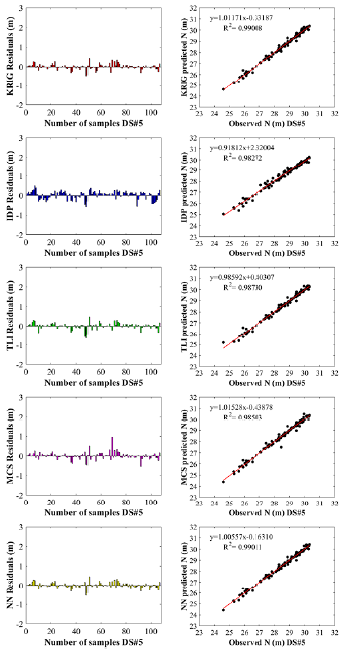
Figure 7 Comparison of the geoid undulation values predicted by GRNN and those observed at the testing phase
According to Table 4, the lowest and highest RMSE values in the training stage were obtained with DS#1 and DS#3, respectively. The lowest MAE value was determined with DS#4 and the highest with DS#3. The highest NSE value at the training stage was determined in DS#1. At the testing stage, the lowest and highest RMSE values were determined with DS#3 and DS#4, respectively. In addition, the lowest and highest MAE values were determined in DS#2 and DS#4, respectively. The lowest and highest NSE values were calculated for DS#4 and DS#3. In order to illustrate the success of the MLR, the predicted geoid undulation values and those observed at the testing stage for each dataset (DS#1, DS#2, DS#3, DS#4, and DS#5) are shown in Figure 8.
Results of interpolation methods
The differences between the predicted and the observed geoid undulation values at the test points for the interpolation methods were computed to determine the RMSE, MAE, and NSE for the five different datasets (DS#1, DS#2, DS#3, DS#4, and DS#5), and are given in Table 5.
Table 5 Statistical findings for the interpolation methods
| Dataset | (DS#1) | (DS#2) | ||||
|---|---|---|---|---|---|---|
| Interpolation methods | RMSE (m) | MAE (m) | NSE | RMSE (m) | MAE (m) | NSE |
| Krig | 0.298 | 0.140 | 0.95226 | 0.239 | 0.127 | 0.97038 |
| IDP | 0.320 | 0.179 | 0.94504 | 0.275 | 0.180 | 0.96082 |
| TLI | 0.301 | 0.149 | 0.95130 | 0.248 | 0.133 | 0.96814 |
| MCS | 0.301 | 0.151 | 0.95146 | 0.251 | 0.140 | 0.96740 |
| NN | 0.298 | 0.143 | 0.95232 | 0.237 | 0.128 | 0.97077 |
| NRN | 0.341 | 0.235 | 0.93746 | 0.291 | 0.219 | 0.95601 |
| LP | 0.296 | 0.159 | 0.95317 | 0.230 | 0.135 | 0.97260 |
| RBF | 0.322 | 0.167 | 0.94438 | 0.268 | 0.151 | 0.96270 |
| PR | 0.477 | 0.363 | 0.87820 | 0.411 | 0.311 | 0.91242 |
| MS | 0.443 | 0.223 | 0.89477 | 0.306 | 0.172 | 0.95134 |
| Dataset | (DS#3) | (DS#4) | ||||
| Interpolation methods | RMSE (m) | MAE (m) | NSE | RMSE (m) | MAE (m) | NSE |
| Krig | 1.406 | 1.020 | 0.02753 | 0.243 | 0.131 | 0.96927 |
| IDP | 1.380 | 0.993 | 0.06381 | 0.255 | 0.166 | 0.96604 |
| TLI | 1.407 | 1.012 | 0.02653 | 0.240 | 0.131 | 0.97014 |
| MCS | 1.416 | 1.026 | 0.01322 | 0.250 | 0.138 | 0.96759 |
| NN | 1.411 | 1.024 | 0.02063 | 0.240 | 0.131 | 0.97007 |
| NRN | 1.427 | 1.045 | -0.00203 | 0.332 | 0.230 | 0.94248 |
| LP | 1.421 | 1.043 | 0.00655 | 0.228 | 0.140 | 0.97287 |
| RBF | 1.404 | 1.026 | 0.03100 | 0.261 | 0.146 | 0.96455 |
| PR | 1.432 | 1.039 | -0.00800 | 0.461 | 0.378 | 0.88948 |
| MS | 1.421 | 1.053 | 0.00677 | 0.291 | 0.170 | 0.95587 |
| Dataset | (DS#5) | |||||
| Interpolation methods | RMSE (m) | MAE (m) | NSE | |||
| Krig | 0.143 | 0.095 | 0.98961 | |||
| IDP | 0.207 | 0.164 | 0.97842 | |||
| TLI | 0.159 | 0.102 | 0.98729 | |||
| MCS | 0.178 | 0.110 | 0.98409 | |||
| NN | 0.142 | 0.097 | 0.98986 | |||
| NRN | 0.275 | 0.217 | 0.96196 | |||
| LP | 0.171 | 0.130 | 0.98532 | |||
| RBF | 0.188 | 0.122 | 0.98214 | |||
| PR | 0.462 | 0.345 | 0.89245 | |||
| MS | 0.404 | 0.206 | 0.91746 | |||
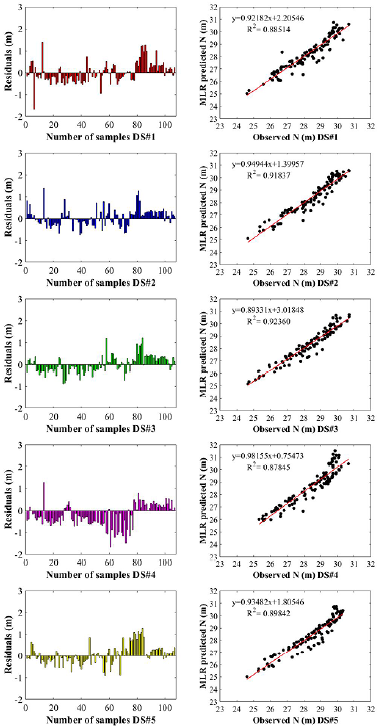
Figure 8 Comparison of the geoid undulation values predicted by MLR and those observed at the testing phase It can be seen from Figure 8 that the a and b values of the predictions made using different datasets yielded close results. Moreover, the figure shows that the determination coefficient (R2) between the observed and predicted values of DS#3 during the testing phase was 0.92360.
According to Table 5, in terms of the resulting RMSE and NSE values, the best performance in the testing phase was obtained for the NN in DS#5. However, the highest RMSE value was found in DS#3 with the PR. In addition, the lowest MAE value was found in DS#5 using the krig method and the highest in DS#3 with the MS. The NSE value in DS#3 was very low with all methods. To demonstrate a comparison of the methods in terms of accuracy, Figure 9 gives the observed geoid undulation values with the values calculated for DS#5 using the interpolation methods.
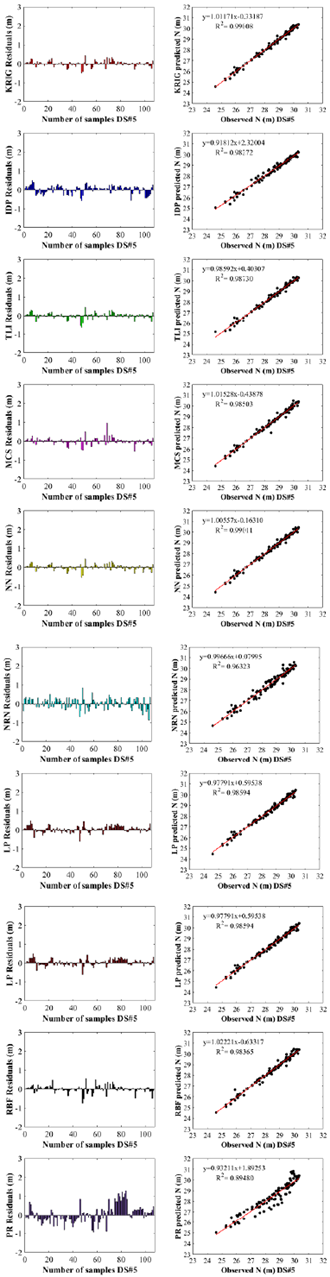
Figure 9 Comparison of the geoid undulation values predicted by interpolation methods with the observed values for DS#5
As can be seen in Figure 9, the a value obtained with the DS#5 using the NN gave a result closer to 1 than the other datasets. Likewise, using the NN, the b value obtained with the DS#5 yielded a result closer to 0 than the other datasets. In the testing phase, the highest R2 among the observed and predicted values was obtained by the NN interpolation method in the DS#5.
Comparison of methods used in geoid undulation prediction (using A-fold cross-validation)
In order to evaluate the general performance of all the methods using the k-fold cross-validation, it was necessary to calculate the averages of the statistical criteria values (RMSE, MAE, NSE, and R2). In other words, the average value was found for each performance criterion result given in Tables 2, 3, 4, and 5. According to the 5-fold cross-validation method based on the average performance values of the statistical criteria, in general, all interpolation methods except PR gave similar results (RMSE, 0.466 m - 0.648 m; MAE, 0.303 m - 0.487 m; NSE, 0.71291 - 0.78283; R2, 0.75789 - 0.82706). The performance of the PR method was weaker than for the other methods. Table 6 shows the average values for the RMSE, MAE, NSE, and R2 obtained from RBFNN, GRNN, MLR, and PR.
Table 6 Average values for the RMSE, MAE, NSE, and R2 (5-fold)
| Method | Phase | RMSE (m) | MAE (m) | NSE | R2 |
|---|---|---|---|---|---|
| RBFNN | Training | 0.030 | 0.018 | 0.99598 | 0.99875 |
| Testing | 0.558 | 0.400 | 0.82036 | 0.85108 | |
| GRNN | Training | 0.029 | 0.010 | 0.99881 | 0.99951 |
| Testing | 0.185 | 0.137 | 0.98229 | 0.98249 | |
| MLR | Training | 0.440 | 0.307 | 0.90522 | 0.90522 |
| Testing | 0.455 | 0.352 | 0.89176 | 0.90080 | |
| PR | Testing | 0.648 | 0.487 | 0.71291 | 0.75789 |
As can be seen from Table 6, on average, the GRNN outperformed all methods investigated for training and testing phases. The best NSE and R2 values (0.99881 and 0.99951) and the lowest RMSE and MAE values (0.029 m and 0.010 m) were found in the GRNN training phase. The GRNN also yielded the lowest RMSE and MAE values (0.185 m and 0.137 m) with the highest NSE and R2 values (0.98229 and 0.98249) for the testing phase. It is clear that the highest RMSE and MAE, and the lowest NSE and R2 values were obtained with the PR during the testing phase. The results of the interpolation methods used with DS#3 negatively affected the performance with the other four datasets and reduced the accuracy (see Table 5). The RBFNN yielded poor overall results when compared to the interpolation methods. Among the methods used in this study, the MLR was ranked second-highest for accuracy. Considering the overall prediction accuracy of the different methods, the GRNN is the one to be recommended for predicting geoid undulation.
Conclusion
In this study, two different ANN methods (RBFNN and GRNN), the MLR, and ten different interpolation methods were comprehensively investigated and analyzed in order to compare their performances in geoid undulation prediction. The k-fold cross-validation method was used to obtain a better generalization. The evaluation of the performance of the datasets using cross-validation can be carried out in two ways: (1) by accepting that the method with the minimum error is the most appropriate one or (2) by considering that the method with the minimum average of results for all the datasets is the most appropriate one. When the methods used with each dataset were compared, the test results using the NN in DS#5 were the most successful. However, the lowest RMSE, MAE, NSE, and R2 values were obtained with the DS#3 using the ten different interpolation methods. In the calculation performed with the same dataset, the most successful method after the NN method was the GRNN, whereas the RBFNN and MLR gave nearly the same results. The GRNN was the most successful method in the evaluation carried out by averaging the RMSE, MAE, NSE, and R2 values produced using the five different datasets. In this study, the analysis of the results of two different performance evaluations for the GRNN demonstrated that the method could be successfully applied and was capable of yielding results equally as accurate as or better than those of the RBFNN, MLR, or interpolation methods used for prediction. Another conclusion that can be drawn from this study is that incorrect point distribution and dataset division can negatively affect the performance of interpolation methods when used in geoid undulation calculation. Therefore, it was recognized that the use of the k-fold cross-validation in geoid undulation calculations could expose incorrect data distribution. It was also shown that the use of the k-fold cross-validation method may give more accurate results for large amounts of data as well as for a sparse number of data. Using the same dataset, the k-fold cross-validation method could also be used to test the effects of other ANN methods and compare them to the results of this study. Moreover, additional studies could analyze geoid undulation prediction using a different dataset with the methods used in this study. It is hoped that the present study will thus contribute to the field and lead to future research on geoid undulation modeling.






























