Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.7 no.13 Medellín Jan./June 2011
Supply channel coordination in a newsvendor model with two allocation quotas
Coordenação de um canal de fornecimento baseado em um modelo de vendedor de jornais com duas cotas atribuídas.
Coordinación de canales de suministro en un modelo tipo newsvendor con dos cupos de reserva
Gerardo Arango Ospina1, César Escalante Coterio2 y Carolina Rendón Aguirre3
1 Doctor en Ciencias Matemáticas, garango@eafit.edu.co, Professor, Universidad EAFIT, Medellín, Colombia.
2 Magíster en Matemáticas Aplicadas, cescalan@eafit.edu.co, Risks Consultant, Delima Marsh, Medellín, Colombia.
3 Magíster en Matemáticas Aplicadas, bathory@hotmail.com, student, Maestría en Ingeniería Matemática, Universidad Carlos III, Madrid, España.
(Recepción: 20-ene-2011. Modificación: 25-feb-2011. Aceptación: 28-feb-2011)
Se aceptan comentarios y/o discusiones al artículo
Abstract
The motivation for this paper arises from an article written by Jianli Li and Liwen Liu [1] in 2007, extending the classical newsvendor model to a supply chain where the dealer, after depletion of an initial order, is given the option of a second order within an allocation quota prescribed and conditioned by the manufacturer. The paper analyzes coordination of the channel in order to improve the expected benefits of the system. This paper extends the model to allow the newsvendor a second allocation quota at the end of the period, under similar conditions. The possibilities and incentives for channel coordination are studied.
Key words: channel coordination, newsvendor model, limited reserve, stochastic programming.
Resumo
A motivação para o presente trabalho provém de um artigo escrito em 2007 por Jianli Li e Liwen Liu [1], que estenderam o problema clássico do vendedor de jornais conformando uma corrente simples de fornecimento na que o varejista faz um pedido para o fabricante, e, se não for satisfeita a demanda, tem a possibilidade de fazer um segundo pedido dentro de uma cota limitada e condicionada pelo fabricante. Eles analisam como estabelecer um mecanismo de coordenação entre as duas partes para que o ganho esperado do sistema seja máximo. Neste trabalho o modelo descrito é ampliado, permitindo que o varejista possa usar uma segunda cota de reserva no final do período, em condições similares, procurando otimizar o ganho esperado do sistema. A possibilidade da coordenação do canal e o mecanismo para consegui-la são estudados.
Palavras chaves: Coordenação de canais, modelo de vendedor de jornais, cotas de reserva, programação estocástica
Resumen
La motivación para este trabajo proviene de un artículo escrito en 2007 por Jianli Li and Liwen Liu [1], quienes extienden el problema clásico del vendedor de periódicos conformando una cadena simple de suministros en el que el minorista realiza un pedido al fabricante, y si éste no satisface la demanda, tiene la posibilidad de realizar un segundo pedido dentro de un cupo limitado y condicionado por el fabricante. Ellos analizan cómo establecer un mecanismo de coordinación entre las dos partes para que la ganancia esperada del sistema sea máxima. En este trabajo se amplia el modelo descrito, permitiendo que el minorista pueda recurrir a un segundo cupo de reserva al final del periodo, bajo condiciones similares, buscando optimizar la ganancia esperada del sistema. Se estudian la posibilidad de coordinación del canal y el mecanismo para lograrla.
Palabras claves: coordinación de canales, modelo newsvendor, cupos de reserva, programación estocástica.
1 Introduction
The classical newsvendor model does not consider the manufacturer risks, that is why some extensions of the model include those risks within the perspective of a supply channel in which each agent makes her own decisions leading, most likely, to policies that are ineffective for the system as a whole. Under the circumstances of the model, the centralization of decision making trough a channel coordination mechanism, usually results in higher expected profits for the system as a whole and for each agent individually.
Supply chains provide a business strategy where wholesalers and retailers work together to improve their profits, while offering lower prices to consumers. Decision making in a supply channel depends on the degree of centralization of the channel. The complexity of decision making in inventory systems within a supply channel is remarkably increased by uncertainty on demand or other relevant variables.
Among others, the following authors have approached the subject of supply chains and coordination mechanism:
Arshinder, Kanda and Deshmukh [2], present a systematic review of the literature to elucidate the importance of supply chain coordination. Their objectives are to report and review various perspectives on SC coordination issues, to understand and appreciate various mechanisms available for coordination and to identify the gaps existing in the literature. A framework is suggested indicating scope for further research.
Thomas and Griffin [3], point out that firms have a chance to reduce their operating costs through coordination of planning of the three fundamental stages of supply chains: procurement, production and distribution. They review the literature addressing coordinated planning between two or more stages of the supply chain, placing particular emphasis on models that would lend themselves to a total supply chain model.
Zhang Long, Song Shiji and Wu Cheng [4], study a supply chain model in which a supplier sells a single product to a retailer who faces the newsvendor problem. The results show that the optimal production quantity with decentralized decision making with a wholesale price contract is less than that with centralized decision making. The advantages and drawbacks of three types of contracts are analyzed with numerical examples.
Weng [5], generalizes the newsvendor model to analyze the coordinated quantity decisions between the manufacturer and the buyer, who cooperate to meet the random demand of one product with a short life cycle. Quantity discounts are developed as incentive policies.
Zimmer [6], investigates the problem by means of a single-period order and delivery planning model within a Just-in-Time setting. The aim of the paper is to find a coordination mechanism that allows the system to perform just as well as a centralized one.
Although Hariga's article [7] is not about channel coordination, it does present an extension of the newsvendor model somehow related to this paper. In most inventory systems it is common practice to hold excess stocks in a rented warehouse whenever the storage capacity of the owned warehouse is insufficient. The purpose of the paper is to study the effect of renting more storage space on the optimal ordering policy in a stochastic single-period setting. It is shown that the optimal ordering quantity obtained from the single-period, two-warehouse model is smaller than the ordering quantity of the unconstrained classical newsboy problem.
Jianli Li and Liwen Liu [1] in 2007 extended the newsvendor model to a supply chain where the dealer, after depletion of an initial order, is given the option of a second order within an allocation quota prescribed and conditioned by the manufacturer. This paper extends the model to allow the newsvendor a second allocation quota at the end of the period, under similar conditions.
The individual (retailer and manufacturer) and system models are introduced in section 2 and solved in section 3. In section 4 channel coordination is studied and a coordination mechanism is proposed. Section 5 summarizes the conclusions.
2 Model description
The demand model corresponds to a highly demanded and volatile product subject to rapid obsolescence due to its dependence on fast changing technological or fashion oriented features. Under the circumstances, lengthy inventory storage is not feasible.
In a supply chain integrated by a manufacturer and a retailer, the latter decides the initial order quantity Q; if total demand exceeds Q, the retailer can place a second order, but she must incur a backorder cost e.g. corresponding to discounts offered to costumers for the wait. In addition, the manufacturer charges a higher price to the second order, because she faces higher manufacturing costs in a second stage. The retailer's second order is limited by an allocation quota M, set by the manufacturer. If demand even exceeds the quota, the retailer can resort to a second allocation quota N at even higher expenses and price than those paid for the first quota. If the demand goes over the second quota, the retailer can place an order up to the quota availability (M + N) and must pay a shortage cost (e.g. a penalty) on excess demand. Finally, at the end of the period, the retailer may receive a salvaging value for each unit of unsold stock.
We want to maximize the retailer's expected profit E[Πb(Q, M , N )] and we denote by Qb the optimal order quantity. The manufacturer's expected profit is E[Πs(Q, M , N)] and the optimal policy, maximizing it is denoted by (Ms, Ns) where Ms and Ns are the optimal capacities reserved in the first and second allocation quotas correspondingly. If manufacturer and retailer are owned by a single firm the expected profit of the centralized system is E[Πj(Q, M , N)] and the optimization problem consists in finding an optimal policy (Qj, Mj, Nj) which maximizes it. What we want to prove is that, for the supply chain, it is better the centralized than the individual decisions.
We use the following notation:
X: Random demand with probability distribution function F(x), density function f(x) and finite mean µ. Clearly X ≥ 0. We assume F(x) to be strictly increasing on its support.
p: Retail unit price.
w,w′ and w′′: Wholesale prices for the first order and the first and second quotas of the second order, correspondingly.
c,c′ and c′′: Unit production costs to fulfill the first order and the first and second quotas of the second order, correspondingly.
k, k′: Retailer's unit backorder costs for the first and second quotas, respectively.
b, b′: Manufacturer's unit cost for the reserve capacity of the first and second quotas, respectively.
v: Unit salvaging cost.
r: Retailer's unit shortage cost.
Q: Retailer's first order quantity.
M : First allocation quota.
N : Second allocation quota.
Notice that although X ≥ 0 by common sense, that condition is not used for any mathematical result obtained in this paper. All the above parameters are supposed to be non negative. Parameters w′′,c′′,k′ and N are specific of the two reserved quotas model. A natural assumption is that p > w′′ > w′ > w > c′′ > c′ > c > v ≥ 0.
A necessary condition for the retailer to place a second order is to have a positive marginal profit i.e. p − w′ − k+ r > 0 for the first quota and p − w′′ − k′ + r > 0 for the second quota. Those conditions are natural and we suppose them for the model to make sense. An analogous consideration on the necessity of positive margins on the side of the manufacturer, leads to conditions w′ − b − c′ > 0 and w′′ − b′ − c′′ > 0 to be assumed from the beginning.
The decision sequence between the two parties goes as follows: the manufacturer informs to the retailer the availability of two allocation quotas (M and N) and the corresponding wholesale prices (w, w′ and w′′). The retailer then decides on the first order quantity Q and the manufacturer, based on that figure, decides on the size of the two quotas.
3 Solution of individual and system models
3.1 Retailer's model
The retailer's profit function Πb (Q, M , N) is therefore:

And the expected profit is

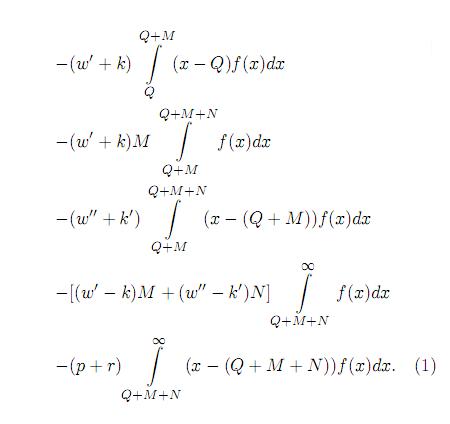
Differentiating with respect to Q we obtain

And the second derivative

Under the condition

holds, showing that Πb(., M , N) is a concave function, whose maximum is attained when (∂ /∂Q)E[Πb(Q, M , N)] = 0. Solving the equation for F(Q) in terms of M and N, we have so proved the following theorem
Theorem 1. If w′′ + k′ > w′ + k, the optimal first order quantity for the retailer is given by Qb, implicitly defined by:

When N = 0 one obtains the quantity corresponding to a single allocation quota (see Li and Liu [1]). Taking M = 0 and N= 0 one obtains the newsvendor classical solution.
3.2 Manufacturer's model
We denote by Πs(Q, M , N) the profits function, M and N are the decision variables andQis set by the retailer. The profit function is:

and the expected profit is


Theorem 2. If w′′ + k′ > w′ + k, the optimal first order quantity for the retailer is given by Qb, implicitly defined by: If
b > b′, w′′ − c′′ − b′ < w′ − c′ − b y w′ − c′ > w′′ − c′′,
The optimal policy for the manufacturer is given by (Ms, Ns), implicitly defined by:

Proof: Differentiating the manufacturer's expected profits with respect to M and N we obtain

Equating to zero both equations and solving we find

The latter equation is (5) and replacing it in the former we obtain (4).
To verify existence and unicity of the solution let us compute

where w′ − c′ > w′′ −c′′ is a sufficient condition for the last equation to hold. The necessity of the two first inequalities in the statement of the theorem comes from the conditions 0 < F(Q + M) < 1. Finally, as

the Hessian matrix ∇2E[Πs(Q, M , N)] is negative definite, therefore the expected value E[Πs(C, M , N)] is a concave function onMandN, and the proof is complete. ⌈ ⟨☙
Although it is fairly clear that the retailer would prefer the reserved capacity to be as big as possible, the manufacturer faces her own conditions to reserve capacity for each quota. The following corollary establish the conditions under which each reserve becomes attractive to the manufacturer.
Corollary 1. In the decentralized system where the retailer and the manufacturer make their own decisions to maximize their expected profit, the manufacturer reserves two allocation quotas if the pair (b, b′) corresponds to an interior point of the triangle with vertices

A necessary condition for the manufacturer to reserve both quotas is the following:
(p + r − v)(w′′ − c′′ )>(p + r−(w′′ + k′ ))(w′ −c′′).
Proof: The retailer's and manufacturer's policies are defined by (2) and by (4) and (5), respectively. The fact that the manufacturer reserves capacity for the two quotas of a second order means that Ms > 0 and Ns > 0 or, equivalently, that the following inequalities are met

The manufacturer to make her decision on reserves assumes that the retailer will adopt its policy, given by (2), and also that

This result shows that b′ is bounded downwards by a linear function of b in this manner
b′ > m1s b + ts,
where,
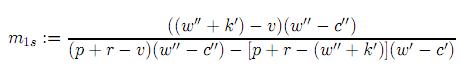
is the slope of the line and

is its intercept.
Replacing in (7) the values of F(Qb +Ms) and F(Qb + Ms + Ns) given by equations (4) and (5), we can obtain the inequality

that, in view of w′ − c′ > 0 and (w′ − c′) − (w′′ − c′′) > 0, is equivalent to

From this inequality we can conclude that b′ can be bounded upwards with a linear function of b in this manner
b′ < m2sb,
where m2s := (w′′ −c′′)/(w′ −c′) is the slope of a line through the origin.
The inequality w′ ′ − c′′ < w′ − c′ implies directly that m2s < 1 and m1s > 1, so the lines b′ = 0, b′ = m1sb + ts and b′ = m2sb intercept at the vertices of a triangle ABC whose interior contains the point (b, b′) meeting inequalities b′ > 0, (8) and (9).
To prove the last statement in the corollary, starting from inequality (8), using inequality (9), we may compute the bound b <[(w−v)/(p+r−v)](w′ −c′) for b. In other words, b is bounded above by the abscissa of the intersection point of the lines b′ = m1sb + s and b′ = m2sb, implying that m1s > 0 and therefore that the inequality (p+r−v)(w′′ −c′′)>(p+r− (w′′ +k′ ))(w′ −c′) must be met as a necessary condition for the manufacturer to reserve the two allocation quotas. Notice that from this inequality follows that ts < 0.
In a strict sense, to finish the proof we should verify that the inequalities stated in theorem 2 do not have a bearing on reserve allocations. In fact, as m2s < 1, at the interior of the triangle b > b′; on the other hand, the line b′ = b− [(w′ −c′) − (w′′ −c′′)] lies to the right of the triangle ABC, as can be easily verified, so implying that the inequality w′′ −c′′ − b′ < w′ −c′ − b holds at the interior of the triangle. ☙
Note that, if (9) is not met, the manufacturer dos not reserve a second quota and, in that case, one can resort to the one single quota model.
3.3 Centralized System
Although the retailer expects a big manufacturer's capacity, she must balance her orders due to the decreasing profit margins. On the other hand the manufacturer expects a big first order but the reserve can improve her profit expectations. As a consequence, in the decentralized system an optimal decision of an agent not necessarily optimizes the expected profit of the other agent. Therefore, the search for a coordination mechanism is possible and desirable to look for an improvement on the interest of both parties. Assuming that the supply chain is owned by a single firm in a centralized system, the owner would like to maximize the expected profits choosing both the first orderQand the two quotas M and N. For the system to reserve capacity for the two allocation quotas it is necessary that both profit margins are positive, i.e. p + r − c′ − k′− b > 0 and p + r − c′′ − k′ −b′ > 0.
The profits function of the system Πj(Q, M , N) is obtained by adding those of the manufacturer and the retailer:

The expected profit is therefore


Theorem 3. If c − v > b, the optimal policy (Qj, Mj, Nj) that maximizes E[Πj(Q, M , N)] is given by:

Proof: The partial derivatives of expected profits with respect to Q, M and N are:

Equating to zero each equation we obtain:
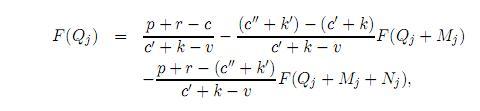

Last equation is (13) that, once being replaced in the second equation, gives (12), and both resulting equations replaced back in the first gives (11).
To verify that the solution corresponds to a maximum, we will use the following notation.

The Hessian matrix of the model ∇2E[Πj(Q, M , N) can be written as

Note that O and R are strictly negative and that, under the additional assumption c′′ + k′ > c′ + k, so is P. Note also that the conditions w′′ + k′ > w′ + k and w′ − c′ > w′′ − c′′, necessary for the functions of expected profits of the retailer and the manufacturer to be concave, imply the additional assumption. Using the criterion of principal minors it can now be shown that ∇2E[Πj(Q, M , N) is a negative definite matrix, hence E[Πj(C, M , N)] is concave on the three variables and as a consequence there exists an optimal policy (Qj, Mj, Nj) maximizing the expected profit. ☙
The theorem provides the information to define the conditions under which the system reserves two allocation quotas.
Corollary 2. In the centralized system, capacity is reserved for the second order if (b, b′) corresponds to an interior point of the triangle with vertices

Proof: The proof is similar to the proof of corollary 1. The fact that the centralized system reserves capacity for both quotas in the second order means that Mj > 0 and Nj > 0, i.e.

Substituting (11), (12) and (13) in inequalities (14) we obtain the inequalities

which are necessary and sufficient conditions for the system to reserve first and second quotas. These inequalities are equivalent to m1jb + tj < b′ < m2jb where

Now, an elementary calculation enables us to obtain the conclusion stated by the corollary.
It is worthwhile noting that, as can be easily verified, triangle ADE is located to the left of the straight line B = c − v > b and, as a consequence the condition stated in theorem 3 do not have a bearing on quota allocations. ☙
If (16) is not valid then the system does not reserve a second quota for the second order and, in this case and we are back in the one quota model.
4 Channel coordination
4.1 Coordination feasibility zone: b vs b′
According to corollaries 1 and 2, assuming that all the remaining parameters have consistent values, only some couples (b, b′) motivate the manufacture or the centralized system to reserve two quotas. For channel coordination to make sense at a point (b, b′), the conditions on both corollaries have to be satisfied simultaneously. Therefore, a direct consequence of them is the following theorem.
Theorem 4. The valid region for channel coordination in the planeb b′, is the intersection of the two triangles ABC and ADE.
Figure 1 illustrates the region valid for (b, b′), given the parameters indicated in section 4.4. Point P4 (1,0.75) is distinguished, as the unique valid one for the chosen parameters b and b′, among all points displayed, Pj, (j= 1, . . . , 4).
4.2 Coordination advantages
From (5) and (13) we can compute

which, in view of p + r − [c′′ + k′]> p + r− [w′′ + k′] > 0 (retailer's second quota positive marginal cost) proves that F (Qj + Mj + Nj) > F (Qs + Ms + Ns). As F (.) is increasing, we obtain Qj + Mj + Nj > Qs + Ms + Ns. The meaning of this is that the supply of the centralized system is bigger than the supply of the decentralized system and, as we will see, the profits of the decentralized system are bigger as well.
If there is a coordination system leading the parties to make decisions similar to the ones of the centralized system, they both can obtain better results. To design such a mechanism we must compare first the overall profits of the two systems.
Theorem 5. As a result of channel coordination the expected profit is increased by the following amount:

Proof: ∆Π(Qj, Mj, Nj ) > 0: The sum of the optimal values of the expected profits of the two agents, EΠb(Qb, Ms, Ns) + EΠs(Qb, Ms, Ns), is an specific value determined by quantities Qb, Ms and Ns in the objective function EΠj(Q, M , N) which maximizes de centralized system, therefore EΠb(Qb, Ms, Ns) + EΠs(Qb, Ms, Ns) ≤ EΠj(Qj, Mj, Nj). Equation (17) is obtained by substituting (1), (3) and (10) in ∆(Qj, Mj, Nj). ☙
4.3 Coordination Mechanism
The goal now is to develop a coordination mechanism allowing both agents to share the incremented expected profit of the system. The mechanism is made possible only if the parties decide to accept it.
It is assumed that the manufacturer takes the lead and offers price incentives to encourage the retailer; in other words, the manufacturer offers a discounted wholesale price wj for the first order, so the retailer orders the optimal quantity Qj. The manufacturer expects a portion α × 100% of the increment on expected profit, where 0 ≤ α ≤ 1. Let Πs(Mj, Nj, wj, Qj) be the manufacturer's expected profit under the policy (Mj, Nj, Qj); we then have

where E[Πs(Qb, Ms, Ns)] and ∆Π(Qj, Mj, Nj) are given by (3) and (17), respectively. Therefore (18) can be written as
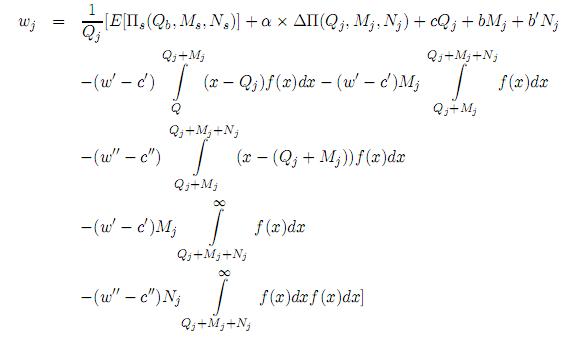
Through the use of the discounted price policywj, the retailer can share (1 − α) ×100% of the increase of expected value, and now her expected profits, denoted by Πb(Qj, wj, Mj, Nj), are
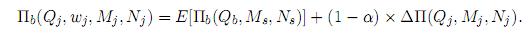
It is clear that the extra profit of the agents depends on α. Therefore, this factor provides convenient alternatives to split the increment of expected profits between the two agents. In real world that factor is determined by the strongest party in the system. It is worthwhile noting that wholesale prices w′ and w′′ for the second order may also be used, in a similar manner, to coordinate the system.
4.4 Example
We use a numerical example to examine the model. It is assumed that the distribution of demand is normal with mean 200 and standard deviation 50. We use the same distribution as in [1] in order to obtain results that are comparable to those of the referenced article but, as it was said in the description of the model, the non negativity of the demand does not have any bearing on the mathematical results.
The parameters are given in table 1.
Taken b= 1 and b′ = 0.75, then (see Figure 1) the point P4(1 , 0.75) is in the valid region for parametersband b′. Table 2 and table 3 summarize the results.
5 Conclusions
5.1 General
1. The allocation of two reserve quotas opens new possibilities for the centralized system to increase the total offer and improve the expected profits of the decentralized system. This makes possible an effective coordination of the channel.
2. The holding costs b and b′ and their relative values confer significance to the model, as shown by the following facts:
• If b′ > b (and b′ > 0), equations (4) and (12) show that the second quota is not feasible, so b > b′ is necessary for the model to be useful. The assumption b > b′ is realistic when the holding unitary costs of the manufacturer have economies of scale (e.g. a concave costs function).
• In both systems, if the holding cost are zero (b = b′ = 0), then F (Q + M + N) = F (Q + M) = 1 and the optimal reserve would be unlimited for the quota with greater marginal profit and null for the other quota. In a similar manner b′ = 0 would justify an unlimited reserve for the second quota.
3. The magnitude of the margin c−v, between the first order production cost and the salvaging value, turns out to be definitive for the existence of possibilities for the centralized system to offer two reserve quotas.
4. It is possible to extend the model by substituting the expected value with other risk measures, such as CV a R.
5. Another extension could be the model with n quotas. A mayor difficulty in that case seems to be the identification of recurrent guidelines to support inductive hypothesis, due to the complexity of the underlying geometric problem. This extension is partially documented in Carolina Rendón's thesis work [8].
6. A third extension could be the optimization of the residual mean.
5.2 About parameters consistency
The parameters must accomplish certain relations among them for the model to make sense.
Good statement of the model
p > w′′ > w′ > w > c′′ > c′ > c > v ≥ 0
Positive marginal costs
Retailers's first quota: p + r − w′ − k > 0
Retailers's second quota: p + r − w′′ − k′ > 0
Manufacturer's first quota: w′ − c′ − b > 0
Manufacturer's second quota: w′′ −c′′ − b′ > 0
System's first quota: p + r − c′ − k− b > 0 − Superflous
System's second quota: p + r− c′′ − k′ − b′ > 0 − Superflous
Concavity of objective functions
Retailer: w′′ + k′ > w′ + k
Manufacturer: w′ − c′ > w′′ − c′′
System: c′′ + k′ > c′ + k − Superflous
Existence of solution
Manufacturer: 0 < F(Q+Ms)< 1 : b > b′ − Superflous
w′ − c′ − b > w′′ − c′′ − b′ − Superflous
Centralized System:
0 < F(Qj)<1: c − b > v − Superflous
c′ + k < c − b − Superflous
0< F (Qj +Mj) < 1: c ′ + k + b <c ′′ +k ′ +b ′ − Superflous
Quotas feasibility
Decentralized System:

Centralized System:

Inequalities labelled as Superflous either can be inferred from the other inequalities or do not have a bearing on decisions concerned with the allocation of the two quotas in any of the two systems.
Acknowledgments: The authors express their gratitude to Professor José Valdés Castro who proposed the model as the first Advisor of Carolina Rendón in her thesis work. They are also thankful to the referee for his relevant and qualified observations that encouraged them to improve the paper.
References
1. Jianli Li and Liwen Liu. Supply chain coordination with manufacturer's limited reserve capacity: An extended newsboy problem. International Journal of Production Economics, ISSN 0925-5273, 112 (2), 860- 868 (2008). 87, 88, 90, 94, 106 [ Links ]
2. Arun Kanda Arshinder and S. G. Deshmukh. Supply chain coordination: Perspectives, empirical studies and research directions. International Journal of Production Economics, ISSN 0925-5273, 115 (2), 316335 (2008). 89 [ Links ]
3. Douglas J. Thomas and Paul M. Griffin. Coordinated supply chain management . European Journal of Operational Research, ISSN 0377-2217, 94 (1), 1-15 (1996). 89 [ Links ]
4. Long Zhang, Shiji Song and Cheng Wu. Supply Chain Coordination of Loss-Averse Newsvendor with Contract. Tsinghua Science And Technology, ISSN 1007-0214, 10 (2), 89 133-140 (2005). [ Links ]
5. Z. Kevin Weng. Coordinating order quantities between the manufacturer and the buyer: A generalized newsvendor model. European Journal of Operational Research, ISSN 0377-2217, 156 (1), 148-161 (2004). 89 [ Links ]
6. Kirstin Zimmer. Supply chain coordination with uncertain just-in-time delivery . International Journal of Production Economics, ISSN 0925-5273, 77 (1), 1-15 (2002). 90 [ Links ]
7. M. A. Hariga. Single period inventory models with two levels of storage. Studies in Advanced Mathematics, 43. Production Planing and Control, ISSN 0953-7287, Online ISSN 1366-5871, 9 (6), 553-560 (1998). 90 [ Links ]
8. Carolina Rendón. Coordinación de una cadena de suministros en un modelo con dos cupos de reserva. Thesis work, Maestría en Matemáticas Aplicadas, Universidad EAFIT, (2009). 108 [ Links ]