Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.8 no.16 Medellín July/Dec. 2012
ARTÍCULO ORIGINAL
Tratamiento de outliers para el estudio de transmisión de vibraciones del ferrocarril
Treatment of Outliers to Study Railway Vibrations Transmission
Nicoletta González–Cancelas1, Francisco Soler-Flores2 Alberto Camarero Orive3 e Íñigo López Ansorena4
1 Doctor Ingeniero de Caminos, Canales y Puertos, nicoletta.gcancelas@upm.es, profesor, Universidad Politécnica de Madrid (UPM)–, Madrid–España.
2 Licenciado en Matemáticas, f.soler@upm.es, investigador, Universidad Politécnica de Madrid. Madrid–España
3 Doctor Ingeniero de Caminos, Canales y Puertos, alberto.camarero@upm.es, profesor, Universidad Politécnica de Madrid, Madrid–España.
4 Ingeniero de Caminos, Canales y Puertos, i.lopeza@alumnos.upm.es, investigador, Universidad Politécnica de Madrid, Madrid–España.
Recepción:03-ago-2012, Aceptación:29-oct-2012
Disponible en línea: 30-nov-2012
MSC: 62-07 / PACS: 89.40.-a
Resumen
En este trabajo se presenta el resulado del análisis de datos de vibraciones inducidas por la propagación de ondas originadas por el paso de trenes, metro y tranvía. Dichos datos han sido tomados con aelerómetros de fibra optica, dentro del marco del proyecto de investigación TRAVIESA (Transmisión de Vibraciones del ferrocarril urbano al entorno: Estrategias, Tecnologías y materiales para su atenuación) financiado por el CDTI y el Ministerio De Ciencia e Innovación del Gobierno de España. La metodología desarrollada permite caracterizar el nivel de las vibraciones que afectan a los diferentes elementos de la infraestructura ferroviaria y los edificios cercanos. La tecnología de los acelerómetros es la fibra óptica y las mediciones fueron realizadas por el Instituto Tecnológico de Óptica, Color e Imagen (AIDO).
Palabras claves: Análisis de datos, outliers, ferrocarril, vibraciones.
Abstract
This paper presents the data analysis of the vibration induced by the propagation of waves caused by passing trains, metro and tram. These data are taken with an optical fiber accelerometer within the framework of the research project TRAVIESA (Transmisión de Vibraciones del ferrocarril urbano al entorno: Estrategias, Tecnologías y materiales para su atenuación) funded by CDTI and the Ministry of Science and Innovation of the Government of Spain. The methodology was developed to characterize the level of vibrations that affect different elements of railway infrastructure and nearby buildings. Optical fiber accelerometers were used and the measurements were made by the Technological Institute of Optics, Colour and Imaging (AIDO).
Key words: Data mining, outliers, railway, vibration.
1 Introducción
La industria ferroviaria europea [1] desarrolla programas para la eficiencia energética y el impacto medioambiental del ferrocarril. Los trenes que circulan a nivel de la superficie, así como los subterráneos, son uno de los medios de transporte masivo más seguros ambientalmente , ya que sus niveles de contaminación y el espacio requerido son reducidos comparados con carreteras de capacidad similar u otros modos de transporte [2]. No obstante, un posible problema de este medio de transporte en zonas urbanas son las vibraciones que generan y los ruidos emitidos. La principal causa de las vibraciones generadas por la circulación de un tren es el contacto rueda-carril, concretamente en las fluctuaciones de la fuerza de contacto provocadas por las irregularidades del perfil de ruedas y carriles [3] . Estas fuerzas dan origen a ondas que se transmiten desde el punto de aplicación hacia la superficie libre [2], ya sea siguiendo un camino directo o tras múltiples reflexiones y refracciones. Las vibraciones pueden generar perturbaciones acústicas y vibraciones en edificios que se convierten en incomodidades para la calidad de vida de las personas.
El paso de trenes a través de las vías genera un gran nivel de tensiones en la estructura ferroviaria debido al aumento de las cargas que se producen por el carácter dinámico de los esfuerzos. Aunque este aumento de las cargas puede tener múltiples focos de origen, sólo se produce debido a la acción de la carga móvil desplazándose por la vía. Para el caso de vías con balasto estos esfuerzos son amortiguados y absorbidos por la capa granular del balasto, que sufre un elevado nivel de vibraciones en sus partículas que puede llegar a afectar su comportamiento mecánico con fenómenos como la licuefacción del balasto, situación que provoca una descompactación de los granos de la capa, y por tanto ve así reducida su capacidad de resistir los esfuerzos generados que se transmiten a través de la traviesa.
El incremento de las velocidades comerciales, en especial con la proliferación de líneas de alta velocidad, también ha llevado consigo un aumento de los movimientos y las vibraciones, que pueden llegar a ser especialmente altas en el caso que la velocidad se aproxime a la velocidad crítica de propagación de ondas en el suelo. La energía transmitida a la estructura se propaga en forma de ondas por la capa de balasto y el terreno por donde discurre la vía a velocidades relativamente bajas en el caso de los suelos blandos, pudiendo ser alcanzadas o incluso sobrepasadas por los trenes de alta velocidad actuales, produciendo un fenómeno de resonancia ([4]). Otro problema derivado del aumento de velocidad de los trenes de alta velocidad es el fenómeno del vuelo de balasto [5], a partir de 300 km/h los flujos de aire turbulentos formados en la zona de los bogies y en los bajos del tren, pueden llegar a ser suficientemente fuertes como para levantar las partículas de la superficie de la capa de balasto, y llegar a golpear los bajos y ruedas del tren, de forma que los granos proyectados van rebotando entre la base del tren y la vía, dañando los equipamientos del vehículo y los carriles.
El aumento progresivo de las velocidades de circulación de los trenes ha hecho aumentar los esfuerzos sobre las capas de asiento de la superestructura, haciéndose necesario (o al menos recomendable) aumentar el espesor de la capa de balasto a 35 cm [6], añadir subcapas, utilizar materiales de mayor calidad y la introducción de elementos elásticos entre los componentes para mitigar las nuevas vibraciones generadas.
Dentro del proyecto de investigación TRAVIESA (Transmisión de Vibraciones del ferrocarril urbano al entorno: Estrategias, Tecnologías y materiales para su atenuación) financiado por el CDTI y el Ministerio De Ciencia e Innovación del Gobierno de España dentro del '' se establece que a tenor de esta situación se hace necesario generar un protocolo de actuación para caracterizar el nivel de las vibracion
Plan Nacional de I+D+i. Programa Nacional de Cooperación Público-Privada. Subprograma de Transporte e Infraestructuraes que afectan a carril, infraestructura de vía (solera, tunel. . . ) y aceras y edificios cercanos, evaluar la influencia del tren (velocidad, tipo, perfil de rueda,. . . ), carril (zona de rodadura) y vía de paso y, finalmente, definir medidas correctoras provisionales.
2 Estado del arte
La velocidad de circulación de los trenes, y más si es en alta velocidad, genera sobre la vía unas solicitaciones verticales superiores a las cargas estáticas habituales. Estas solicitaciones mayores provienen del paso de una carga por un punto a una cierta velocidad, pero también se ven aumentadas por las condiciones y características de la vía, los vehículos y su equipamiento. De esta forma estos esfuerzos dinámicos se pueden ver muy ampliados, y análogamente la deformaciones que generan, llegando a rangos de ser hasta tres veces superiores que la produciría una carga de igual magnitud en reposo . Estas diferencias entre el estado dinámico y el estático en una vía de ferrocarril, se muestran comparando las cargas por eje (en reposo) y la carga registrada en la vía mediante sensores de tensión. Lim, W. (2004) [7] realizó pruebas en Colorado,Nueva York y Washington. Se apreció en ambos casos cómo a partir de pesos por eje alrededor de 200 kN las cargas dinámicas se hacen cada vez mayores, incrementándose respecto a las estáticas.
Estas medidas representan cómo la velocidad, las pequeñas irregularidades y daños, afectan de forma directa a la excitación dinámica, ampliando su magnitud, y en consecuencia el rápido deterioro de la vía, haciendo aumentar las cargas dinámicas progresivamente.
Aunque no es el único origen de las excitaciones dinámicas, muchas irregularidades que las causan se dan en los contactos entre elementos de la vía, como el contacto rueda-carril, o el traviesa-balasto. Este conjunto de elementos que forma la totalidad de la vía ha llevado a los estudios a representar todo el comportamiento de forma ideal con modelos matemáticos. La interacción dinámica entre vehículo y carril (en esfuerzos verticales) puede representarse de forma razonable mediante multitud de modelos. La figura 1 da un ejemplo claro de un modelo discreto de suspensión del vehículo por muelles y amortiguadores, una viga soportada por otro sistema de mulles y amortiguadores que representa el sistema placa de asiento-traviesa-balasto, y finalmente el sistema de contacto hertziano para describir el contacto entre rueda y carril. Esveld, C. (2001) [8].
El comportamiento dinámico produce vibraciones a un gran rango de frecuencias. Desde las más bajas, del orden de 0, 5 - 1 Hz debidas a las aceleraciones verticales y laterales del tren, hasta 200 Hz como consecuencia de irregularidades en el carril y las ruedas.
La suspensión primaria entre el sistema rueda-eje y el bastidor es el primer elemento del vehículo que reduce las vibraciones creadas por el contacto ruedacarril. Con la suspensión secundaria se busca la reducción de frecuencias más bajas, y se encuentra entre el bastidor del bogie y el bastidor principal del vehículo. De forma análoga se puede entender el sistema de suspensión de la estructura, puesto que se puede considerar el sistema sujeción-placa de asiento como la suspensión primaria, y la capa de balasto como la suspensión secundaria. Por esta razón es de vital importancia la reducción de los pesos no suspendidos en el vehículo. Como más se consigue bajar estos pesos, más se reduce el efecto dinámico del paso del tren. De forma análoga se ha constatado la importancia de la elasticidad de la placa de asiento en cuanto a la reducción de vibraciones que llegan a la estructura. De todas formas los modelos dinámicos acostumbran a ser muy complejos, y por eso la mayoría de estudios se limitan al estudio de estos fenómenos con consideraciones cuasiestáticas.
Las vibraciones ocasionadas por el tránsito de trenes han sido estudiadas experimentalmente desde mediados del siglo XIX. Ya en 1864, South [9] publicó los estudios realizados acerca del nivel de vibración inducidas por el ferrocarril a su paso por el túnel de Watford.
Más recientemente se han realizado varios estudios sobre vibraciones ocasionadas por trenes circulando a velocidades medias. Dawn y Stanworth [10] midieron el nivel de vibraciones en una estructura situada a 42 metros de la vía, Melke y Kramer [11] midieron las aceleraciones de vibración originadas por un tranvía en vía, suelo y en el túnel. Xia et al. [12] obtuvieron respuestas ante el paso de un ferrocarril de dos edificios; la amplitud de las vibraciones aumentaban con la velocidad del tren y se atenuaba con la distancia de la vía, además se comprobó que las plantas altas de los edificios vibraban más que las inferiores. Además el estudio concluye que los trenes más pesados, de mercancías, inducen mayores vibraciones que los ligeros, de pasajeros.
En la última década, muchos investigadores se han dedicado al estudio de las vibraciones ocasionadas por el tráfico ferroviario, tales como el estudio reciente desarrollado por García-Bennet et Al. [13] y se han desarrollado diferentes modelos analíticos, numéricos y experimentales para poder caracterizar el paso del ferrocarril en el suelo y en estructuras cercanas a la vía como el estudio desarrollado recientemente por Zhoi [14] para el metro de Shangai y sus edificios colindantes .
La velocidad es un factor determinante en la amplificación de esfuerzos sobre la vía, pero también a la vista de los datos no se debe relacionar directamente (y sin ningún matiz) el incremento de la velocidad con el aumento de las vibraciones. En una vía en buen estado, un tren puede circular a 300 km/h generando un nivel de vibraciones y esfuerzos admisibles ([15]). Por contra, si la estructura ferroviaria está en mal estado, un tren circulando a 200 km/h puede provocar unas vibraciones y unos incrementos de tensiones mayores que los que producía el paso del otro tren a 300 km/h (velocidad notablemente más alta), pero con una vía en buenas condiciones [5].
En casos donde se producen resonancias, esto es todavía más claro, ya que los picos de deformación no son incrementados proporcionalmente a la velocidad sino que responden a otros factores, y se ven amplificados para ciertas velocidades determinadas.
En este sentido un adecuado mantenimiento de la vía, el uso de materiales adecuados y un diseño correcto son factores determinantes en cuanto a generación de esfuerzos dinámicos, y en consecuencia durabilidad de la vía.
El paso de trenes genera unos esfuerzos en la capa de balasto que aceleran sus partículas dándoles una vibración que pueden llegar a ser muy altas en el caso de la alta velocidad, y que afectan en gran medida a su comportamiento y su capacidad de reacción respecto los esfuerzos transmitidos por la traviesa. El exceso de esfuerzo dinámico en la capa de balasto puede causar la pérdida de rozamiento entre partículas, perdida de contacto entre caras de traviesa, perdida de rigidez vertical y resistencia lateral.
Este rápido deterioro de la estabilidad del lecho de balasto puede provocar el movimiento del carril y por tanto de la vía, perdiendo alineación y calidad geométrica en general.
El comportamiento del balasto bajo un efecto vibratorio depende de la velocidad, de la aceleración que llegan a tener las partículas de balasto dentro de la capa y de la geometría de las mismas. Así pues, como demostraron Morgan y Markland (1981)[5] una cierta vibración aplicada al material granular puede incrementar su resistencia portante y nivel de compactación en una vía. Los resultados del experimento de Karrech (2008) [16] estarían en concordancia con este hecho, ya que gracias a la aplicación de una carga cíclica a frecuencias no muy altas, las partículas de balasto se mueven y recolocan, provocando un asiento inicial, pero que consolidan el material granular de forma que se evitan asientos posteriores. De forma sencilla se podría explicar que este empaquetamiento es análogo a la precarga que se realizaría para mejorar la capacidad portante en un suelo blando.
Sin embargo, como se cita en [5], el comportamiento depende de las condiciones y características de la carga aplicada. Así como en casos de carga reducida a frecuencias bajas durante un período de tiempo reducido, se obtiene un efecto positivo, no siempre es así y los problemas aparecen cuando, a partir de aceleraciones del orden de 0,7 - 0,8g , el material granular empieza a sufrir un fenómeno de descompactación, perdida de fricción en los contactos de los granos, formación de espacios vacíos mayores, y empieza a comportarse como un fluido, haciendo que los desplazamientos verticales aumenten y disminuya la resistencia lateral de la vía. Así, el resultado definitivo es la pérdida de capacidad portante y resistente de la vía.
A partir de este umbral de 0,8g, donde ya se nota la pérdida de capacidad portante del material granular, el nivel más crítico se produce al llegar entre 1, 4 y 1, 6g donde se produce la licuefacción total del balasto, y este pasa a comportarse como un fluido. Además se ha constatado mediante los ensayos que realizaron los Ferrocarriles Franceses que la aceleración máxima en el interior de la capa de balasto es mayor que la aceleración aplicada en la superficie de la capa ensayada. Estas diferencias podían llegar a ser del 15 %. Esto explicaría por qué se da una inestabilidad al balasto al llegar a 0.8g ya que se deduciría que en el interior de la capa, la aceleración tiene un valor próximo a 1g (0,8 x 1,15 â 1g). Las vibraciones y aceleraciones que recibe la capa de balasto han sido un factor determinante en el mantenimiento que se ha venido realizando en las líneas de alta velocidad con balasto alrededor del mundo. El nivel de vibraciones sufrido ha provocado el continuo empeoramiento de la vía, teniendo que realizar periodicamente labores de bateo y alineación para mantener la calidad geométrica aceptable, ya que las vibraciones son más acusadas cuanto menor es la calidad geométrica. Pero estos trabajos de mantenimiento han provocado a su vez el deterioro más rápido de los granos de balasto, su rotura y desgaste. De esta forma, se produce un deterioro continuo de la estructura granular. En la primera línea de alta velocidad, el Tokaido japonés se tuvo que realizar una renovación total de la capa de balasto a los 13 años de la puesta en servicio, y en la línea francesa París-Lyón , la sustitución total se realizó a los 15 años. Esto ha provocado intensas discusiones sobre hasta qué punto es efectivo el balasto para líneas de alta velocidad, y el coste de su mantenimiento. Hasta llegar al extremo que Japón construye sus líneas con vía en placa desde 1980, y sólo algunos tramos específicos se realizan con balasto, y parece que Alemania seguirá también esta tendencia de construir vía en placa. En España todas las vías se proyectan con balasto, y ya se cumplieron los 15 años de la puesta en servicio de la línea Madrid-Sevilla, momento en que fue necesario proceder a su sustitución y renovación como en el caso japonés y francés.
Gracias a las nuevas técnicas de introducción de elementos elásticos por toda la estructura (incluso llegando a combinar el uso de todas ellas), ya se ha conseguido que sea posible construir una vía con balasto con las suficientes garantías como para que, con un diseño adecuado, los niveles de vibración propagados y ejercidos sobre el material granular sean suficientemente bajos como para que no se produzca un deterioro prematuro, y las operaciones de mantenimiento tengan que ser todavía necesarias, pero menos regulares.
Para una vía de ferrocarril construida encima de un terreno relativamente blando (como arcillas o turbas), las ondas que se propagan por la superficie de balasto acostumbran a tener cierta longitud, del orden de 5 a 20 metros([5]). Estas longitudes de onda largas están causadas debido a la naturaleza blanda del substrato. Pero cuando la estructura se sitúa encima de un sistema más duro, como formaciones rocosas, tableros de puentes, túneles, las ondas propagadas no se limitan sólo a un espectro de onda larga. Esto es debido a que en un soporte rígido, las ondas son reflejadas de nuevo hacia la superestructura. De esta forma, la capa de balasto en un puente o en la solera de un túnel, actúa como una guía de ondas, tanto de larga como de corta longitud [8].
Las ondas más cortas que se desplazan por el balasto pueden tener una longitud similar a la magnitud de las partículas del dicho balasto, pudiendo de esta forma alterar granos de forma individual. En los modelos numéricos usados para simular el comportamiento micro-mecánico, en pruebas de simulación de cargas móviles, se ha demostrado que en capas de balasto consistentes en partículas de mayor tamaño, se intensifica la radiación de ondas, especialmente cuando la capacidad de amortiguación del balasto es baja.
La intensidad de la radiación depende de la velocidad, así a velocidades más altas, el balasto es perturbado de forma menos individual y por el contrario, cuando estas velocidades son menores , la intensidad de la radiación es dependiente de la velocidad, de forma que estas perturbaciones individuales pueden tomar más importancia, haciendo perder la estructura empaquetada de la capa de balasto.
Esta amortiguación de la capa de balasto depende generalmente de dos aspectos:
• La fricción entre partículas.
•Distribución del tamaño de partículas en la capa.
En el primer caso, cuando la fricción de partículas es alta (por ejemplo en balasto bien angulado), una importante cantidad de energía es disipada en el contacto entre partículas, lo que significa una alta capacidad de amortiguación.
El segundo aspecto se refiere al hecho que una cierta distribución adecuada de las partículas impide que se concentren en un tramo granos de un solo tamaño, evitando así fenómenos de resonancia, donde la longitud de onda pueda coincidir con el tamaño de las partículas dominantes presentes.
Las ondas más relevantes que se producen son las provocadas por una carga móvil (en este caso el tren) que se desplaza por un semiespacio elástico. Principalmente, al paso de la carga por este semiespacio se producen tres tipos de ondas que se van propagando por el terreno: las ondas P, las ondas S y las ondas de Rayleigh . (Esveld 2001)[8].
En las ondas P (primarias o de compresión) las partículas se mueven en la dirección de la propagación, en las ondas S (secundarias o de cortante) las partículas se mueven en dirección perpendicular a la propagación, mientras que las ondas de Rayleigh se forman en la superficie libre y llevan asociado un movimiento elíptico de las partículas.
Sus diferencias también se hacen visibles en cuanto a las velocidades de propagación (C) distintas que tienen cada una de ellas, siendo su orden de magnitud el siguiente (ecuación 1)

Al ser CR el valor más bajo de propagación, resulta ser el valor de la Velocidad Crítica del tren, ya que es la velocidad mínima donde se empieza a producir el fenómeno de resonancia ya comentado.
Gracias a la mecanica de medios continuos, y teniendo en cuenta que el subespacio es un material isotropo, se puede calcular con relativa facilidad los valores de Cs y Cp para distintos tipos de suelo, mediante las siguientes formulas (2 y 3) :

Siendo ρ la densidad del suelo, y λ, μ las constantes de Lamé que caracterizan el comportamiento elastico del material y que se pueden obtener experimentalmente, aunque resulta mas facil obtenerlas a partir de otras propiedades elasticas como el Modulo de Young (E) y el Coeficiente de Poisson (ν) (4)

El módulo de deformación transversal G (5):

La dependencia de la velocidad de propagacion de las ondas de estos valores caracteristicos de cada tipo de terreno, indican hasta que punto la respuesta de la propagacion de ondas dependera de por que tipo de material se mueven. Por ejemplo, en terrenos como arcillas blandas o material organico Cs puede llegar a tener valores entre 150 y 250 km/h, pero para terrenos mas duros como arenas densas, toma valores de 400-500 km/h, e incluso velocidades mucho mayores para terrenos rocosos. Naturalmente estos valores correspondientes a suelos mas competentes, estan todavia lejos del rango de velocidades comercial de los trenes de alta velocidad.
Pero en general las amplificaciones dinámicas no son solo causadas por la velocidad del tren, sino tambien por irregularidades en la via, distancia entre los ejes del bogie, etc. En el caso de la via en balasto situada encima de una base rigida, la energia transmitida por las vibraciones de la via permanece dentro de la capa de balasto debido a las multiples reflexiones que se producen en este substrato mas duro.
Como a consecuencia de esto, las ondas reflejadas pueden interferir con otras (reflejadas o no), pudiendo causar el aumento o disminucion de amplitudes segun sea la interaccion entre ellas. Si se llega al caso de que estas vibraciones se superponen con las generadas por el paso del tren, la via puede entrar en resonancia provocando deformaciones muy grandes, a velocidades considerablemente mas bajas de la denominada Velocidad Critica referida solo al efecto del paso del tren a gran velocidad, aunque hay que reconocer que es un fenomeno muy poco probable.
El aumento de la velocidad de los trenes actuales esta acompañado también por el aumento de las deformaciones en la vía, balasto y subsuelos, y pueden llegar a ser especialmente altas cuando el tren se aproxima a las velocidades de onda críticas de la vía o el suelo. Estos movimientos pueden ser muy altos llegando a afectar en gran medida la estabilidad y operabilidad de la vía, estructuras cercanas como postes de soporte de la catenaria o incluso edificios colindantes.
Aunque puede haber diferentes velocidades críticas para una misma vía, dependiendo de la configuración de ésta y de en qué medio se propagan las ondas, la más baja es la más importante debido a que es la primera que el tren encuentra a medida que acelera. La correspondiente a las ondas Rayleigh de superficie que se presentan en el subsuelo debajo del balasto es la mínima de todas ellas, aunque también existen las ondas de velocidad de fase de la vía soportada por el balasto. Una se denomina velocidad crítica del suelo y la otra velocidad crítica de la vía respectivamente, y dependiendo del terreno, ambas pueden ser fácilmente excedidas por los modernos trenes de alta velocidad, especialmente en zonas de suelo muy blando, donde ambas velocidades de propagación resultan ser muy bajas.
Tal y como predijo Krylov [17] en diferentes estudios realizados con modelos matemáticos durante 1994 y 1995, si el tren sobrepasa la velocidad de propagación de las ondas Rayleigh (CR) en el suelo de la base, y debido a la acumulación de energía bajo el tren, como se mostraba en la figura 2, ocurre un boom que lleva asociado un incremento muy elevado de las vibraciones del suelo. Este fenómeno es análogo al boom sónico de los aviones que superan la velocidad del sonido. Gracias a eso, ahora mismo ya es posible hablar en la práctica de trenes 'supersónicos' o más correctamente trenes 'Trans-Rayleigh'. Las ondas se propagan por el terreno de forma análoga a la del tren, haciendo que la energía se acumule bajo la zona de los bogies (ecuación 6),

Dónde G es el Módulo de deformación transversal y Ï es la densidad del terreno
Un Outlier se define como aquella observación (o conjunto de observaciones) inconsistentes con el resto del conjunto de datos [18] . Es decir, aquella observación que siendo atípica y/o errónea, tiene un comportamiento muy diferente con respecto al resto de los datos frente al análisis que se desea realizar sobre las observaciones experimentales
En estas definiciones conviene observar las siguientes peculiaridades:
• Las observaciones atípicas y erróneas exigen que los errores o variabilidades sean grandes
• Los outliers no consideran todas las observaciones atípicas o erróneas, sino aquellas que tienen un comportamiento muy diferente respecto al resto de los datos.
Ello viene motivado a raiz de que las técnicas o procedimientos para determinar o corregir este tipo de observaciones sólo tienen sentido en estas situaciones, ya que aquellas observaciones que no tienen un gran error o que se comportan como la mayoría, no van a afectar de forma determinante a las conclusiones que se realicen a partir de las mismas.
Algunos de los métodos clásicos utilizados para la identificación de outliers son:
• Método basado en el recorrido intercuartílico.
• Diagrama Box & Whisker (Cajas y bigotes).
• Método basado en la mediana de las desviaciones absolutas (MEDA).
Los modelos de tratamiento de outliers han sido utilizados en el análisis de datos aplicado a modelos de ingeniería en diferentes trabajos de los autores de este trabajo( [19]). Además el estudio de outliers ha sido un denominador común en diferentes estudios relacionados con este trabajo. Alippi, C.; Casagrande, E.; Fumagalli, M.; Scotti, F.; Piuri, V.; Valsecchi, L. [20] utilizaron el tratamiento de outliers en su metodología para el estudio mediante scanner laser y tratamiento de imágenes para el estudio del desgaste y deformación de los perfiles del carril para detectar los errores en las mediciones. Worden en el año 2000 [20] utilizó el tratamiento de outliers para la detección de valores dañinos para vibraciones. Recientemente Akpinar, B.; Gülal, E. [20] utilizan el estudio de outliers para el procesamiento de los datos para su alternativa a los estudios geodésicos para controlar la geometría del carril.
En este trabajo hemos basado nuestro procedimiento de detección de outliers en el basado en la desigualdad de Tchebychev con un tratamiento estratificado descrito a continuación:
El método de detección de outliers propuesto, se basa en la desigualdad de Tchebychev, P(|X - μ| > kσ) ⤠ y estos vienen dados como los registros pertenecientes al complementario del siguiente conjunto: {xi/|xi -
y estos vienen dados como los registros pertenecientes al complementario del siguiente conjunto: {xi/|xi -  | < kσ} que verifiquen que f(xi) ⥠1 -
| < kσ} que verifiquen que f(xi) ⥠1 -  de donde se deduce que en el intervalo (
de donde se deduce que en el intervalo ( - kσ,
- kσ,  + kσ) se encuentran al menos el 100(1 -
+ kσ) se encuentran al menos el 100(1 -  % de las observaciones (no outliers) y si k es tal que 1 -
% de las observaciones (no outliers) y si k es tal que 1 -  es próximo a 1 , las observaciones fuera de (
es próximo a 1 , las observaciones fuera de ( - kσ,
- kσ,  + kσ) pueden ser considerados como como outliers.
+ kσ) pueden ser considerados como como outliers.
Así, mediante este método obtenemos dos conjuntos de observaciones en cada caso de estudio, estos son el conjunto de observaciones identificadas como outliers y el conjunto de observaciones que no entran en el anterior.
3 Metodología
Para conseguir determinar la respuesta frente a vibraciones de diferentes tramos de ferrocarril, en función de la distancia respecto de la vía y para cada uno de los ejes en los que miden las aceleraciones los sensoores empleados, el grupo de Investigación Logística , Explotación del Transporte y Gestión Operativa (LET&GO) del Departamento de Ingeniería Civil. Transportes de la Escuela de Ingenieros de Caminos, Canales y Puertos de la Universidad Politécnica de Madrid con las mediciones del Instituto Tecnológico de Óptica, Color e Imagen (AIDO) ha desarrollado la siguiente metodología:
1. Descripción de las variables.
2. Identificación de vibraciones extremas mediante outliers.
3. Estudio descriptivo y gráficos de amplitud de aceleraciones.
4. Criterio diferenciador.
En el marco del proyecto TRAVIESA se realizaron medidas de niveles (energía) de vibración y frecuencias de excitación en vía mediante redes de fibra óptica, y se midieron los perfiles del carril con la finalidad de caracterizar (longitud de onda y amplitud) el desgaste ondulatorio que existe en cada carril estudiado para determinar el amortiguamiento necesario. De esta manera y mediante un modelado de soluciones se compararon los registros obtenidos con el fin de seleccionar y clasificar el comportamiento de cada una de ellas. La medición de estas vibraciones en diferentes configuraciones permitió valorar la adecuación de diferentes secciones para distintos tipos de usos y entornos.
Este artículo resume los resultados obtenidos y la metodología empleada en el análisis de los datos obtenidos de las mediciones.
El estudio se realizó en tramos de tranvía, metro y ferrocarril del sistema ferroviario español. Este artículo corresponde al estudio de metro (tramo 1) con las siguientes características: en las tres secciones de este tramo se tiene vía en placa de hormigón (taco de hormigón) con carril UIC 54, fijación SKL 1, acabado en hormigón y traviesas bibloque Stedef-vsb.
El tipo de terreno es:
• Mioceno: Materiales margosos y materiales rocosos calizos calcareníticos
• Cuaternario y Pliocuaternario: rellenos antrópicos, depósitos coluvioaluviales de gravas con arenas y limos y depósitos tipo glacis de gravas arenosas.
Las dos primeras secciones se ubican dentro del casco urbano. Una de ellas es inmediatamente previa al inicio del un tramo subterráneo y la otra es una sección dentro de la propia estación (Tabla 1).
Las secciones del tramo de estudio se caracterizan por:
• Sección 1.1: La primera sección, se sitúa inmediatamente previa al inicio del tramo subterráneo y después de un viaducto que salva una luz aproximada de 180 metros. Se trata de una recta con pendiente de -0.033 %. En ella se colocaron paneles atenuantes del ruido para mitigar en lo posible las molestias derivadas a las edificaciones cercanas, además de una manta de elastómero de poliuretano, bajo losa, con el fin de impedir en lo posible la transmisión de vibraciones al entorno. Cada una de estas mantas está colocada bajo losa, rodeando el emparrillado de cada una de las dos vías.
• Sección 1.2: En cuanto a la segunda sección, se ubica exactamente sobre la estación subterránea de modo que en las vías junto al propio andén se medirán estas vibraciones al paso de circulaciones. Al contrario que en la anterior, esta sección no dispone de manta antivibratoria recogiendo el emparrillado de vía, por lo que será interesante, siendo una sección similar a la anterior, comparar las mediciones de vibración en ambas.
• Sección 1.3: La tercera sección del tramo subterráneo que se pretende estudiar es la de la estación. La sección posee una configuración constructiva similar a la de las dos anteriores, disponiendo también de manta de elastómero de poliuretano bajo losa para aislar de las vibraciones. Las características de los elementos que la componen son iguales a las secciones anteriores descritas.
Los dispositivos de medición de vibraciones pueden basarse en diferentes tecnologías, la empleada en el proyecto se basa en el empleo de redes de fibra óptica con sensores interferométricos que permiten la realización de mediciones de microdesplazamientos en tres dimensiones, relacionados con el registro temporal a elevada frecuencia de lectura para la valoración de la amplitud y frecuencia de vibración, centrándose en dos rangos de especial interés: la banda de 0 a 20 Hz y de 20 a 80 Hz para el análisis de diferentes fenómenos de generación-transmisión-recepción de vibración.
3.1 Descripción de las variables
El estudio se realizó tomando medidas a diferentes distancias del plano de la vía de las vibraciones producidas en tres ejes: eje perpendicular a la vía (Eje Y) , eje pararelo a la vía (eje X) y perpendicular al plano de la vía (eje Z).
En la tabla 2 se listan las fechas correspondientes a las diferentes campañas de campo realizadas desde noviembre de 2009 a marzo de 2011, en diferentes periodos, para poder abarcar un mayor número de posibilidades de explotación, pero siempre respetando la planificación general del proyecto TRAVIESA.
Para la toma de datos de las aceleraciones se realizaron diversas campañas de campo. Las medidas in situ, en vías de explotación normal de territorio español, se tomaron con diferentes sensores, en cada una de las secciones del tramo de estudio (sección 1.1, sección 1.2 y sección 1.3), para cada unas de las distancias al carril y para cada uno de los ejes de estudio. A continuación se describen en detalle las variables con su notación.
Las variables analizadas en este estudio son las siguientes (Tabla 3):
La variable 'tipo-tren' estudia los siguientes casos (Tabla 4)
Los 'tipo-vía' estudiados son (Tabla 5)
Los 'velocidades' estudiadas son (tabla 6)
El 'Dirección del tren' se caracteriza como aparece en la tabla 7:
Se analizaron 92 registros que constituyen 517 mediciones con un total de aproximadamente 275 millones de registros.
Para el análisis de las vibraciones en el tramo de estudio, dividido a su vez en tres secciones(sección 1.1,sección 1.2 y sección 1.3) se realizan mediciones para las distancias señaladas en la tabla 8. Estas distancias se encuentran condicionadas por la posibilidad de medición y colocación de los sensores empleados, además de por la propia explotación de la línea.
3.2 Identificación de vibraciones extremas mediante outliers
Los datos de las mediciones originales vienen dados en unidades propias de los sensores. Así, a partir de los valores de las mediciones se calculan las aceleraciones asociadas a los datos brutos que proporcionan los sensores. Para el cálculo de las aceleraciones producidas por el paso de los trenes se tienen en cuenta las unidades de medición y se utiliza la siguiente expresión (7):
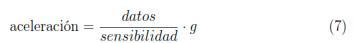
Una primera aproximación para la detección de datos anómalos que en principio puedan identificarse con vibraciones extremas o fuera del rango normal de las vibraciones producidas por el tren, se identifican mediante el cálculo de outliers a diferentes porcentajes (70 %, 75 %, 80 %, 85 %, 90 %, 95 %) de la variable aceleración. En la figura 3 puede verse un ejemplo de una medición completa en uno de los ejes de estudio y a una distancia determinada (los valores outlier están señalados en rojo).
Las unidades en las que miden los diferentes acelerómetros empleados en las campaña de campo se caracteriza como aparecen en la tabla 9.
3.3 Estudio descriptivo y gráficos de amplitud de aceleraciones
Una vez programado el cálculo de aceleraciones, todos los datos se encuentran en las mismas unidades y es posible realizar un estudio descriptivo y comparativo de los datos.
En esta parte de la investigación se desarrollan los estudios descriptivos de los datos (media, desviación, p75, p80, p85, p90, ri, mínimo, máximo, amplitud) (tabla 10), y se asocian las variables que caracterizan la medición o registro de aceleraciones para un momento dado, una sección concreta y a una distancia determinada en un eje de medida. La amplitud de aceleración en cada medición se selecciona como variable criterio diferenciador y se aplica en el paso siguiente de la metodología.
Para completar el estudio descriptivo de los datos, se realizan histogramas de frecuencias (figura 4) y un gráfico que denominamos de máximos, que ordena las mediciones de menor a mayor y que permiten observar la amplitud de la mediciones de aceleraciones (figura 5).
3.4 Criterio diferenciador
Una vez seleccionado el criterio diferenciador, que corresponde al estudio de la amplitud de las aceleraciones, se puede comparar las observaciones y seleccionar los casos extremos mediante el tratamiento de outliers.
Para la obtención de conclusiones sobre los casos en los que se producen amplitudes de aceleración anómalas, a cada distancia y en cada uno de los ejes de estudio, se establece el siguiente criterio: Los outliers que superan a determinados porcentajes de la población de los resultados descriptivos de los casos agrupados por tramo, dirección de la medición y distancia a la vía . En la figura 6, se presenta el caso particular del gráfico de outliers al 85% de la amplitud de aceleraciones medido con un sensor situado a 0.4 metros del carril y en la dirección perpendicular al plano de la vía (eje Z).
4 Resultados y conclusiones
Una vez desarrollada la metodología, con el objetivo de determinar la respuesta frente a vibraciones de vías con diferentes elementos constructivos, se recogen a continuación los resultados para cada uno de las diferentes secciones, para las diferentes distancias a las que se sitúan los sensores de medición y en cada uno de los ejes estudiados.
Siguiendo la estructura de la metodología en la tabla 11 se recogen los resultados del estudio de amplitud de aceleraciones para el caso: distancia 0,4 metros y eje X pararelo a la vía.
Del estudio de la amplitud de las aceleraciones a las diferentes distancias de medición, para el eje Z (perpendicular a la vía), a cualquier distancia de la vía, las secciones que presentan mayores vibraciones son las secciones de metro sobre traviesa con manta elastomérica, vía sobre hormigón, tanto en la estación como la en la marquesina exterior, tanto con el tren entrando en la estación como saliendo de la estación, que corresponden a la marquesina exterior y a la sección 'mercado' (sección 1.1 y sección 1.3).
En el caso de estudio del eje perpendicular a la vía, a cualquier distancia del la vía, las secciones que presenta mayores amplitud de aceleración son las secciones de metro sobre traviesa con manta elastomérica, vía sobre hormigón, en la estación como la en la marquesina exterior, para el tren entrando en la estación (sección 1.1 y sección 1.3).
Por último, para el eje paralelo a la vía, a cualquier distancia del la vía, las secciones que presenta mayores vibraciones son las secciones de metro sobre traviesa con manta elastomérica, vía sobre hormigón, en la estación como la en la marquesina exterior, para el tren entrando en la estación.
Conclusiones adicionales son:
• Las mayores vibraciones se producen para los tramos de vía sobre hormigón, con manta, para cualquier distancia de las estudiadas.
• Las mayores vibraciones se producen en el eje Z, y las menores en los eje perpendicular y paralelo a la vía casi por igual
• A partir de los 2 metros de distancia las vibraciones son prácticamente insignificantes para los ejes perpendicular y paralelo a la vía. Para el eje Z no se encuentra diferencia entre las vibraciones del terreno con o sin presencia de tren.
Para el conjunto de tramos estudiados la función que mejor ajusta la amplitud a las diferencias distancias corresponde a una función potencial del tipo siguiente y = a.xb con a > 0 y b < 0 donde x es la distancia e y la amplitud de aceleración. Lo que concluye un decrecimiento exponencial de las vibracione a partir de los 2 metros de distancia a la vía. El coeficiente de correlación toma valores elevados para los tres ejes de medición.
Agradecimientos
La investigación que ha dado lugar a este artículo se desarrolla dentro del Proyecto ''Traviesa: transmisión de vibraciones del ferrocarril urbano al entorno: estrategias, tecnologías y materiales para su atenuación'' dentro del Plan Nacional de I+D+i. Programa Nacional de Cooperación Público-Privada. Subprograma de Transporte e Infraestructura. Duración, desde: 2008, hasta: 2011. Cuyo Investigador responsable por parte de la Universidad Politécnica de Madrid es D. Alberto Camarero Orive.
Las mediciones de los datos han sido realizadas por el Instituto Tecnológico de Óptica, Color e Imagen (AIDO), es una asociación industrial privada sin ánimo de lucro creada a iniciativa empresarial en 1988 e impulsada por la Generalitat Valenciana a través del Instituto de la Pequeña y Mediana Industria Valenciana (IMPIVA) con la misión de aportar soluciones Tecnológicas a las empresas mediante la óptica industrial.
Agradecemos a la Universidad Politécnica de Madrid el apoyo al desarrollo de las actividades del Grupo de Investigación de Logística y Explotación del Transporte y Gestión Investigación Operativa LET & GO, grupo de investigación que ha desarrollado este proyecto.
Referencias
1. C. Cheron, M. Walter, J. Sandor, E. Wiebe, ''ERRAC Roadmap. Towards 2030: Energy, Noise and Vibration European Railway Roadmaps'', Procedia - Social and Behavioral Sciences, vol. 48, pp. 2221-2229, 2012. [ Links ] Referenciado en 192
2. T. Montalvo, L. E. Suárez, ''Evaluación de las vibraciones del suelo causadas por trenes subterráneos usando elementos finitos''. Revista Internacional de Desastres Naturales, Accidentes e Infraestructura Civil, vol. 2, n.o 1, pp. 79-88, 2002. [ Links ] Referenciado en 192
3. J. Otero Yugat, J. Martínez, MA. De los Santos, S. Cardona, ''Modelo global de la dinámica de contacto rueda-carril para determinar la vibración de un punto del carril al paso de un tren'', Scientia et Technica, vol. 2, n.o 34, may 2007. [ Links ] Referenciado en 192
4. J. Domínguez. Barbero, J. Goicochea, y J. M. G. Ruigómez, ''Valoración de efectos dinámicos en puentes de ferrocarril: la resonancia en líneas de alta velocidad'', Revista de Obras Públicas: Organo profesional de los ingenieros de caminos, canales y puertos, n.o 3428, pp. 39-50, 2002. [ Links ] Referenciado en 193
5. A. Vidal Muro, ''Vibraciones en las vías del ferrocarril'', Universitat Politècnica de Catalunya, Barcelona, 2009. [ Links ] Referenciado en 193, 196, 197, 199
6. M. Fernández, S. Hernández Alonso, A. Ruiz Rúa, ''Para altas velocidades ¿Vía con o sin balasto?'', Revista de Obras Públicas, vol. 147, n.o 3401, pp. 29-40, 2000. [ Links ] Referenciado en 193
7. W. Lim, ''Mechanics of railway ballast behaviour'', University of Nottingham, UK, 2004. [ Links ] Referenciado en 194
8. C. Esveld,Modern Railway Track. MRT-Productions Zaltbommel, 1989. [ Links ] Referenciado en 195, 199, 200
9. J. South, ''Experiments, Made at Watford, on the Vibrations Occasioned by Railway Trains Passing through a Tunnel'', Proceedings of the Royal Society of London, vol. 13, pp. 65-83, ene. 1863. [ Links ] Referenciado en 196
10. TM. Dawn, C. Stanworth, ''Ground vibrations from passing trains'', Journal of Sound and Vibration, vol. 66, n.o 3, pp. 355-362, oct. 1979. [ Links ] Referenciado en 196
11. J. Melke, S. Kramer, ''Diagnostic methods in the control of railway noise and vibration'', Journal of Sound and Vibration, vol. 87, n.o 2, pp. 377-386, mar. 1983. [ Links ] Referenciado en 196
12. H. Xia, N. Zhang, YM. Cao, ''Experimental study of train-induced vibrations of environments and buildings'', Journal of Sound and Vibration, vol. 280, n.o 3-5, pp. 1017-1029, feb. 2005. [ Links ] Referenciado en 196
13. M. Zhou, K. Wei, S. Zhou, J. Xiao, Q. Gong, ''Influence of Different Track Types on the Vibration Response of the Jointly-Built Structure of Subway and the Buildings'', China Railway Science, n.o 2, pp. 33-40, 2011. [ Links ] Referenciado en 196
14. J. Yugat Otero, J. Martínez, M. A. de los Santos, S. Cardona, ''Modelos para la generación y transmisión de vibraciones al paso de un tren'', Scientia et Technica, vol. 5, n.o 37, pp. 261-266, dic. 2007. [ Links ] Referenciado en 196
15. J. Gutierrez, ''El tren de alta velocidad y sus efectos espaciales'', Investigaciones Regionales, n.o 5, pp. 199-221. [ Links ] Referenciado en 196
16. A. Karrech, ''Comportement des matériaux granulaires sous vibration - Application au cas du ballast'', Ecole des Ponts ParisTech, Paris, 2007. [ Links ] Referenciado en 197
17. V. Krylov, ''Generation of ground vibrations by superfast trains'', Applied Acoustics, vol. 44, n.o 2, pp. 149-164, 1995. [ Links ] Referenciado en 202
18. V. Barnett, T. Lewis, Outliers in Statistical Data, 2.a ed. Wiley Series in Probability and Mathematical Statistics.Applied Probability and Statistics, Chichester: Wiley, 1984. [ Links ] Referenciado en 203
19. F. Soler Flores, J. Pardillo Mayora, R. Jurado Piña, ''Tratamiento de outliers en los modelos de predicción de accidentes de tráfico'', in VIII Congreso de Ingeniería del Transporte, España, 2008. [ Links ] Referenciado en 204
20. C. Alippi, E. Casagrande, M. Fumagalli, F. Scotti, V. Piuri, L. Valsecchi, ''An embedded system methodology for real-time analysis of railways track profile'', in Proceedings of the 19th IEEE Instrumentation and Measurement Technology Conference, 2002. IMTC/2002, 2002, vol. 1, pp. 747-751. [ Links ] Referenciado en 204





























