ARTÍCULO ORIGINAL

doi:10.17230/ingciencia.11.21.11

Seismic Data Compression Using 2D Lifting-Wavelet Algorithms

Compresión de datos sísmicos usando algoritmos lifting-wavelet 2D

Carlos Fajardo¹, Oscar M. Reyes² and Ana Ramirez³

1 Universidad Industrial de Santander, Bucaramanga, Colombia, cafajar@uis.edu.co.

2 Universidad Industrial de Santander, Bucaramanga, Colombia, omreyes@uis.edu.co.

3 Universidad Industrial de Santander, Bucaramanga, Colombia, anaberam@uis.edu.co.

Received: 06-10-2014 | Acepted: 02-12-2014 | Online: 30-01-2015

MSC:68P30, PACS:93.85.Rt

Abstract

Different seismic data compression algorithms have been developed in order to make the storage more efficient, and to reduce both the transmission time and cost. In general, those algorithms have three stages: transformation, quantization and coding. The Wavelet transform is highly used to compress seismic data, due to the capabilities of the Wavelets on representing geophysical events in seismic data. We selected the lifting scheme to implement the Wavelet transform because it reduces both computational and storage resources. This work aims to determine how the transformation and the coding stages affect the data compression ratio. Several 2D lifting-based algorithms were implemented to compress three different seismic data sets. Experimental results obtained for different filter type, filter length, number of decomposition levels and coding scheme, are presented in this work.

Key words: seismic data compression; wavelet transform; lifting

Resumen

Diferentes algoritmos para compresión de datos sísmicos han sido desarrollados con el objetivo de hacer más eficiente el uso de capacidad de almacenamiento, y para reducir los tiempos y costos de la transmisión de datos. En general, estos algoritmos tienen tres etapas: transformación, cuantización y codificación. La transformada Wavelet ha sido ampliamente usada para comprimir datos sísmicos debido a la capacidad de las ondículas para representar eventos geofísicos presentes en los datos sísmicos. En este trabajo se usa el esquemaLifting para la implementación de la transformada Wavelet, debido a que este método reduce los recursos computacionales y de almacenamiento necesarios. Este trabajo estudia la influencia de las etapas de transformación y codificación en la relación de compresión de los datos. Además se muestran los resultados de la implementación de diferentes esquemas lifting 2D para la compresión de tres diferentes conjuntos de datos sísmicos. Los resultados obtenidos para diferentes tipos de filtros, longitud de filtros, número de niveles de descomposición y esquemas de compresión son presentados en este trabajo.

Palabras clave: compresión de datos sísmicos; transformada wavelet; lifting

1 Introduction

The main strategy used by companies during the oil and gas exploration process is the construction of subsurface images which are used both to identify the reservoirs and also to plan the hydrocarbons extraction. The construction of those images starts with a seismic survey that generates a huge amount of seismic data. Then, the acquired data is transmitted to the processing center to be processed in order to generate the subsurface image.

A typical seismic survey can produce hundreds of terabytes of data. Compression algorithms are then desirable to make the storage more efficient, and to reduce time and costs related to network and satellite transmission. The seismic data compression algorithms usually require three stages: first a transformation, then a uniform or quasi-uniform quantization and finally a coding scheme. On the other hand, decompression algorithms perform the inverse process of each one of these steps. Figure 1 shows the compression and decompression schemes.

The transformation stage allows de-correlating the seismic data, i.e., the representation in terms of its coefficients (in the transformed domain) must be more compact than the original data. The wavelet transform offers well recognized advantages over other conventional transforms (e.g., cosine and Fourier) because of its multi-resolution analysis with localization both in time and frequency. Hence this family of transformations has been widely used for seismic data compression [1],[2],[3],[4].

There is no compression after the transformation stage when the number of coefficients is the same as the number of samples in the original data. In lossy compression algorithms the stage that follows the transformation is an approximation of the floating-point transform coefficients in a set of integers. This stage is called quantization [5]. As will be seen in section 4, a uniform quantizer is generally used in seismic compression [2],[6],[7],[3].

Finally, a coding scheme is applied to the quantized coefficients. The coding scheme is a lossless compression strategy. It seeks a data representation with a small number of bits. In seismic data compression, the most used coding schemes have been Huffman [8],[9],[10],[11] and Arithmetic Coding [3],[12],[13],[7]. Sometimes a Run Lengh Encoding (RLE) [14] has been used prior to the entropy coding stage [8],[11],[7].

Different methods have been proposed to compress seismic data. The goal has been to achieve higher compression ratios at a quality above 40 dB in terms of the signal to noise ratio (SNR). Since each one of those algorithms uses different data sets, the comparison among them becomes difficult. This paper presents a comparative study for a specific set of seismic data compression algorithms.

We analyzed the wavelet-based algorithms using the lifting scheme, followed by a uniform quantization stage and then by a coding scheme. We have selected the lifting scheme since it requires less computation and storages resources than the traditional discrete wavelet transform (DWT) [15].

In this comparative study, we examined how the variation of some parameters affects the compression ratio for the same level of SNR. The parameters of interest in this paper are the type and length of the wavelet filter, the number of levels in the wavelet decomposition, and the type of coding scheme used. Our results are presented using graphics of compression ratio (CR) versus SNR. The implemented algorithms were tested on three different seismic datasets from Oz Yilmaz's book [16], which can be downloaded from Center for Wave Phenomena (ozdata.2, ozdata.10 and ozdata.28 respectively)¹. Those datasets are shot gathers, i.e., seismic data method traditionally used to store the data in the field. Figure 2 shows a section of each dataset.

This article is organized as follows. Section 2 gives a brief overview of data compression. Sections 3 to 5 examine how the compression ratio is affected by each one of the three mentioned stages. Finally, the last section presents discussion and conclusions of this work.

2 Data compression

According to the Shannon theorem, a message of n symbols (a₁,  a₂,  …,  a_n) can be compressed down to nH bits, on average, but no further [17], where H is called the entropy, a quantity that determines the average number of bits needed to represent a data set. The entropy is calculated by Equation 1, where P_i is the probability of the occurrence of a_i.

The entropy is larger when all n probabilities are similar, and it is lower as they become more and more different. This fact is used to define the redundancy (R) in the data. The redundancy is defined as the difference between the current number of bits per symbol used (H_c) and the minimum number of bits per symbol required to represent the data set (Equation 2).

In simple words, the redundancy is the amount of wasted bits -unnecessary bits- in the data representation. There are many strategies for data compression, but they are all based on the same principle: compressing data requires reducing redundancy.

Two important quantitative performance measures commonly used in data compression are the traditional signal to noise ratio (SNR) and the Compression Ratio (CR). The SNR is expressed in dB and defined by:

Where S_n is the original data and S^′_n is the decompressed data. The CR is defined as:

2.1 Seismic data compression

The seismic data can be considered as a combination of three types of components: geophysical information, redundancy, and uncorrelated and broadband noise [18],[2]. In this way, different strategies to compress seismic data aim to decrease the redundancy.

3 The compression ratio according to the lifting-wavelet used

The DWT has traditionally been developed by convolutions, and its computational implementation demands a large number of computation and storage resources. A new approach has been proposed by Swelden [15] for wavelet transformation, which is called the lifting scheme. This mathematical formulation requires less computation and storage resources than the convolutional implementation.

Basically, the lifting scheme changes the convolution operations into matrix multiplications of the image with complementary filters and it allows for in-place computation, thus reducing the amount of both computation and storage resources [19]. At each step of the lifting method, the image is filtered by a set of complementary filters (i.e., a low-pass filter and its complementary high-pass filter) that allows perfect reconstruction of the image. In the next step of lifting the low-pass filtered image is again filtered by set of complementary filters, and so on. Each step of the lifting scheme can be inverted, so that the image can be recovered perfectly from its wavelet coefficients. The rigorous mathematical explanation of the wavelet transform using the lifting scheme can be found in  [20],[15],[21].

We now show the use of the wavelet transform for compressing seismic data.

Figure 3 shows a histogram obtained from a seismic data set before and after a wavelet transform (using 6.8 biorthogonal filters). Clearly, from Figure 3, the wavelet transform data has a narrower distribution. Its entropy is 6.1 bits per symbol (See Equation 1), while the entropy for the original data is 7.4 bits per symbol, meaning that the wavelet transform data has a better chance to reach an improved compression ratio. In order to generate the histogram, the samples were converted from single precision floating point to integers and the frequencies were normalized.

Thus, the transformation stage allows de-correlating the seismic data, i.e., the representation in terms of wavelet coefficients is more compact than the original one.

3.1 The type of filter To classify the compression ratio according to the selected type of filter, we used three different types of filters and we varied their lengths, and their number of vanishing moments. The types of filters used were: Biorthogonals (Bior), Cohen-Daubechies-Feauveau (CDF) and Daubechies (Db). The experiments were performed in the following order:

2D lifting-wavelet decomposition (1-level) using different filters.

Uniform quantization from 6 to 14 quantization bits. Each mark in the figures corresponds to a number of quantization bits.

Huffman entropy coding.

Figures 4 to 6 show the performance of the algorithms based on Biorthogonals (Bior), Cohen-Daubechies-Feauveau (CDF) and Daubechies (Db). For simplicity we only show three filters for each dataset (low, medium and high performance). However, we observed that for each type of filter there is a range of vanishing moments that achieves a better performance.

Daubechies filters with a number of vanishing moments either 4 or 5, Biorthogonal filters with a number of vanishing moments from 5 to 8, and CDF filters with a number of vanishing moments from 3 to 5 achieved a better performance. These number of vanishing moments were required for both the decomposition filter and the reconstruction filter. In all cases, when either fewer or more of these vanishing moments were used, a lower CR was achieved.

3.2 The number of the decomposition levels

2D lifting-wavelet decomposition, using different levels of decomposition (From 1 to 7)

Uniform quantization using 12 quantization bits.

Huffman entropy coding.

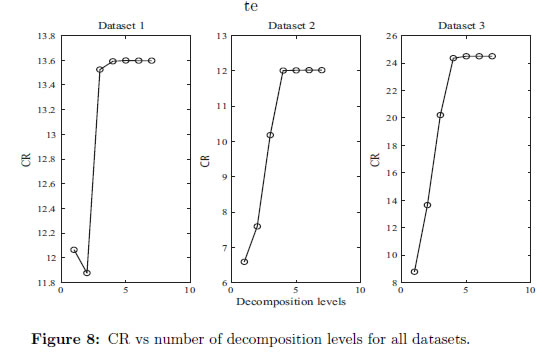
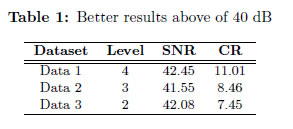
Note in Figure 8 that as the number of decomposition levels increases, the CR increases. This is true for all datasets, until a particular number of decomposition levels is reached. After that level of decomposition, the compression ratio holds almost constant. However, it is important to remark that as the number of decomposition levels increases, the SNR is reduced due to the loss of quality in the quantization process (Section 4). Therefore, it is necessary to choose the best compression ratio above 40 dB (in terms of SNR) among the different levels of decomposition. Table 1 summarizes our best results for each dataset.

4 The quantization stage

The wavelet transform stage reduces the entropy of the seismic data, but no compression has occurred so far, due to the fact that the number of coefficients is the same as the number of samples in the original seismic data. Achieving compression requires an approximation of the floating-point transform coefficients by a set of integers. This stage is called scalar quantization.²

The quantization stage, denoted by y_i=Q(x), is the process of mapping floating-point numbers (x) within a range (a,b) into a finite set of output levels (y₁,y₂, ... , y_N ). Depending on how the y_i's are distributed, the scalar quantizer can be uniform (Figure 9a) or non-uniform (Figure 9b).

A uniform quantizer is traditionally used in seismic compressing [2],[6],[7], [3], because the larger errors in the non-uniform quantization scheme are concentrated in the larger amplitudes (see Figure 9b), and usually the larger amplitudes for the seismic data contain the relevant geophysical information. On the other hand, the small amplitudes in the seismic data have a good chance to be noise. Thus, a uniform quantizer achieves the minimum entropy in seismic applications [5],[23]. An additional gain of using a uniform quantizer is its low computational complexity.

Mapping a large data set into a small one results in lossy compression. As the number of output levels is reduced, the data entropy is also reduced i.e., we increase the possibility to compress the data (Section 2). However, after the quantization stage, a reduction in the SNR occurs due to the approximation process. Here the number of quantization bits determines the number of output levels 2n. Figure 10-left shows how the compression ratio increases as the number of quantization bits is reduced, and Figure 10-right shows that the SNR is decreases as the number of quantization bits is reduced.

5 The compression ratio according to the coding scheme

Once the uniform quantizer is used, the data encoder needs to be selected. In this work, an entropy encoder is used in order to achieve good compression. The entropy coding stage is a lossless compression strategy. It seeks to represent the data with the lowest number of bits per symbol [24]. To classify the compression ratio according to the coding scheme, we tested two different coding schemes on the three data sets. The experiments were performed in the following order:

2D Lifting-Wavelet decomposition (1 level) using a 6.8-Biorthogonal filter.

Uniform quantization from 6 to 14 bits.

Huffman and Arithmetic coding.

Figure 11 shows the performance of the algorithms based on Huffman and arithmetic coding scheme (CR vs SNR). Additionally, Figure 11 shows the maximum CR achieved when the entropy of the quantized wavelet coefficients is used.

As is shown in Figure 11, the Arithmetic coding is very close to the maximum compression ratio, however, above 40 dB both Huffman and Arithmetic achieve a high performance.

6 Conclusions

One of the main goals of this paper is to attempt to know how both the transform stage and the coding stage affect the compression ratio.

Regarding the wavelet filter used, it seems that the performance, in terms of the SNR obtained for a given CR, is not associated with the type of filter, because it is possible to obtain a good compression performance using different types of wavelet filters (e.g., Bior, CDF or Db). However, our results suggest that the performance is related to the the number of vanishing moments of the wavelet filter. Furthermore, the more appropriate number of levels of decomposition can not be established, since the compression ratio did not improve for a particular number of decomposition levels. Previous results suggest that a moderate number of decomposition levels can be used and still we can get enough compression ratio.

The Arithmetic coding showed a superior performance for low levels of SNR. This codification scheme was very close to the maximum CR. However, for values of SNR above 40 dB, which is the level generally required, the performance of both Huffman and arithmetic coding showed similar performance and both were very close to the maximum CR. However, we consider that further research on selecting the best coding method based on the data and the previously transformation and quantization selected stages requires further analysis. This remains as an open problem for the seismic data compression. Further, it is important to remark that the arithmetic coding has a higher computational complexity than the Huffman coding. From the computational complexity perspective, the Huffman coding could be a better option, when the aim is to achieve a SNR above 40 dB.

We implemented several compression algorithms in order to study the influence of both the transform and the coding stage on the compression ratio. We underlined the importance of the number of vanishing moments in the wavelet filter and a moderate number of decomposition levels. In the quantization stage, we selected the uniform quantization, which is appropriate for seismic data since it helps to minimize errors in the geophysical information. Finally, we selected a Huffman coding which gives a high compression ratio with an SNR above 40 dB, and reduces the computational complexity in comparison to the arithmetic coding.

Acknowledgements

1 Available at: http://www.cwp.mines.edu/cwpcodes/data/oz.original/

2 The scalar term refers to each coefficient is independently approximated 

References        [ Links ]

[2] M. A. T, ''Towards an Efficient Compression Algorithm for Seismic Data,'' Radio Science Conference, 2004., pp. 550-553, 2004.         [ Links ]

[3] W. Wu, Z. Yang, Q. Qin, and F. Hu, ''Adaptive Seismic Data Compression Using Wavelet Packets,'' 2006 IEEE International Symposium on Geoscience and Remote Sensing, no. 3, pp. 787-789, 2006.         [ Links ]

[4] F. Zheng and S. Liu, ''A fast compression algorithm for seismic data from non-cable seismographs,'' 2012 World Congress on Information and Communication Technologies, pp. 1215-1219, 2012.         [ Links ]

[5] A. Gercho and R. Gray, Vector quantization and signal compression. Kluwer Academic Publiser, 1992.         [ Links ]

[6] P. Aparna and S. David, ''Adaptive Local Cosine transform for Seismic Image Compression,'' 2006 International Conference on Advanced Computing and Communications, no. x, pp. 254-257, 2006.         [ Links ]

[7] J. M. Lervik, T. Rosten, and T. A. Ramstad, ''Subband Seismic Data Compression: Optimization and Evaluation,'' Digital Signal Processing Workshop Proceedings, no. 1, pp. 65-68, 1996.         [ Links ]

[8] A. a. Aqrawi and A. C. Elster, ''Bandwidth Reduction through Multithreaded Compression of Seismic Images,'' 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum, pp. 1730-1739, May 2011.         [ Links ]

[9] W. Xi-zhen, T. Yun-tina, G. Meng-tan, and J. Hui, ''Seismic data compression based on integer wavelet transform,'' ACTA SEISMOLOGICA SINICA, vol. 17, no. 4, pp. 123-128, 2004.         [ Links ]

[10] A. A. Vassiliou and M. V. Wickerhouser, ''Comparison of wavelet image coding schemes for seismic data compression,'' in Optical Science, Engineering and Instrumentation'97. International Society for Optics and Photonics, 1997, pp. 118-126.         [ Links ]

[11] P. L. D. J. D. Villasenor, R. A. Ergas, ''Seismic Data Compression Using High-Dimensional Wavelet Transforms,'' in Data Compression Conference, 1996., 1996, pp. 396-405.         [ Links ]

[12] X. Xie and Q. Qin, ''Fast Lossless Compression of Seismic Floating-Point Data,'' 2009 International Forum on Information Technology and Applications, no. 40204008, pp. 235-238, May 2009.         [ Links ]

[13] A. Z. Averbuch, F. Meyer, J. O. Stromberg, R. Coifman, and A. Vassiliou, ''Low bit-rate efficient compression for seismic data.'' IEEE transactions on image processing : a publication of the IEEE Signal Processing Society, vol. 10, no. 12, pp. 1801-1814, 2001.         [ Links ]

[14] D. Salomon, Data Compression The Complete Reference, 4th ed.   Springer, 2007.         [ Links ]

[15] W. Sweldens, ''Lifting scheme: a new philosophy in biorthogonal wavelet constructions,'' in SPIE's 1995 International Symposium on Optical Science, Engineering, and Instrumentation.   International Society for Optics and Photonics, 1995, pp. 68-79.         [ Links ]

[16] O. Yilmaz, Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data.   Society of Exploration Geophysicists, 2008.         [ Links ]

[17] C. E. Shannon, ''A Mathematical Theory of Communication,'' The Bell System Technical Journal, vol. XXVII, no. 3, pp. 379-423, 1948.         [ Links ]

[18] L. C. Duval and T. Rosten, ''Filter bank decomposition of seismic data with application to compression and denoising,'' SEG Annual International Meeting Soc. Expl. Geophysicists, pp. 2055-2058, 2000.         [ Links ]

[19] K. Andra, C. Chakrabarti, T. Acharya, and S. Member, ''A VLSI Architecture for Lifting-Based Forward and Inverse Wavelet Transform,'' Signal Processing, IEEE Transactions on, vol. 50, no. 4, pp. 966-977, 2002.         [ Links ]

[20] M. Jansen and P. Oonincx, Second generation wavelets and applications.   Springer, 2005.         [ Links ]

[21] W. Sweldens, ''Wavelets and the Lifting Scheme : A 5 Minute Tour,'' ZAMM-Zeitschrift fur Angewandte Mathematik und Mechanik, vol. 76, no. 2, pp. 41-47, 1996.         [ Links ]

[22] D. L. Fugal, Conceptual Wavelets in Digital Signal Processing: An In-depth, Practical Approach for the Non-mathematician.   Space & Signals Technical Pub., 2009.         [ Links ]

[23] 2 plus 43 minus 4 T. Chen, ''Seismic Data compression: a tutorial,'' 1995. [Online]. Available: http://www.cwp.mines.edu/Documents/cwpreports/cwp-180.pdf         [ Links ]

[24] D. Salomon, Variable-length Codes for Data compression. Springer, 2007.         [ Links ]