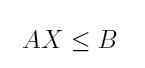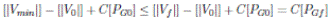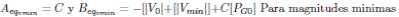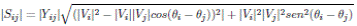1 Introducción
En los sistemas de potencia actuales se ha venido promoviendo el uso de energías renovables como la solar y la eólica con el fin de reducir las emisiones que surgen al generar energía con plantas a base de hidrocarburos. La principal desventaja de este tipo de energía es la aleatoriedad de la velocidad del viento y la radiación solar que hace que no sea certero programar con antelación un despacho económico. Es entonces necesario utilizar algoritmos rápidos que programen un despacho económico óptimo cuando hay una alta incertidumbre de las inyecciones de energía por parte de los paneles solares y los aerogeneradores eólicos, y así se permitan simular una alta cantidad de posibles escenarios 1),(2.
De esta manera el problema corresponde a una optimización de una función objetivo y unas restricciones que se deben cumplir, para los diferentes escenarios aleatorios de las potencias inyectadas renovables 1),(2),(3),(4. En el presente escrito se propone el uso de la función f mincon de M atlab para realizar el despacho económico de un sistema de potencia con penetración de energías renovables. Para el flujo de potencia requerido para la comparación de la formulación propuesta con los resultados presentados se utilizó M atpower5. De esta manera, se considera una función objetivo multivariable no lineal, una restricción de igualdad no lineal, y restricciones de desigualdad lineales. Las inyecciones de energía renovable se suponen con costo cero, y los generadores del sistema disputan el despacho faltante con el propósito de que el costo total de generación sea mínimo y que no se violen las restricciones del sistema, como lo son los limites de las potencias activa y reactiva generadas, la magnitud de las tensiones en los nodos y la cargabilidad de las líneas que los interconectan. De estas restricciones mencionadas, en este articulo se propone una formulación de las mismas haciendo que se puedan escribir como una desigualdad lineal. Adicionalmente, se debe cumplir la restricción de igualdad de la potencia generada total con demandada de todos los nodos sumado a las pérdidas en las líneas.
Para la restricción de pérdidas y demanda se usaron diferentes coeficientes de pérdidas analizados en 6),(7),(8),(9),(10. Especificamente en 10 se muestran los resultados de cálculo de las pérdidas cuando se usan los coeficientes de kron, los incrementales y los coeficientes obtenidos después de aplicar el algoritmo de optimización heurística DEEPSO (Differential Evolutionary Particle Swarm Optimization) que los calcula para diferentes casos de variación de demanda y de generación 11),(12),(13 . De esta manera, el presente artículo es una continuación del trabajo presentado en 10 extendiendo la formulación a su aplicación en el despacho económico y formulando unas restricciones lineales a partir de las restricciones tradicionales (sección 2). Los resultados de la metodología se obtuvieron a partir de simulaciones realizadas para un sistema de 8 nodos que se especifica posteriormente (sección 3).
2 Formulación del problema y deftnición de las restricciones del Sistema
El propósito del despacho económico es minimizar la función costo total de generación, para un sistema donde operan Ng generadores, que viene dada por ((14),(15),(16),(17),(18)):
Se suele aproximar la función costo en cada generador como una función cuadrática de la potencia generada cuando se trabajan generadores convencionales (para generadores renovables esta función puede ser mas compleja al considerar el costo de indertidumbre 19),(20), es decir que la ecuación de costo para la planta Pgi viende dada por:
donde αi, βi y γi son constantes que determinan la forma de la parabola de la función de costo.
De esta manera, la formulación del problema de optimización se escribe como:
sujeto a las restricciónes:
Donde 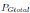 , PDtotal, y PLtotal son las potencias activas generadas, demandadas y perdidas totales del sistema, respectivamente. Los vectores Vmin y Vmax tienen dimensión Nx1 donde N es el número de nodos del sistema, y representan los límites permisibles de las magnitudes de las tensiones para cada nodo. El vector Smax tiene dimensiones Rx1 dónde R es el número de ramas que unen los nodos del sistema, el vector tiene los valores de cargabilidad máxima de estado estable de las líneas que unen los nodos del sistema. Finalmente Pmin, Qmin, Pmax y Qmax son vectores que guardan los valores límites de potencia activa y reactiva generadas que se definen por las condiciones de las centrales generadoras.
, PDtotal, y PLtotal son las potencias activas generadas, demandadas y perdidas totales del sistema, respectivamente. Los vectores Vmin y Vmax tienen dimensión Nx1 donde N es el número de nodos del sistema, y representan los límites permisibles de las magnitudes de las tensiones para cada nodo. El vector Smax tiene dimensiones Rx1 dónde R es el número de ramas que unen los nodos del sistema, el vector tiene los valores de cargabilidad máxima de estado estable de las líneas que unen los nodos del sistema. Finalmente Pmin, Qmin, Pmax y Qmax son vectores que guardan los valores límites de potencia activa y reactiva generadas que se definen por las condiciones de las centrales generadoras.
El problema de optimización mencionado se debe solucionar para los diferentes escenarios de potencia inyectada de los generadores eólicos y solares. Para ello se utiliza matlab, específicamente el script llamado F mincon que permite definir el problema de optimización de la forma:
Donde X es el vector que guarda la solución final de variables que minimizan la función objetivo @obj correspondiente a los costos del sistema, M in es el valor del mínimo, X0 es el punto de partida para la búsqueda de la solución del problema, los vectores Xmin y Xmax, establecen valores mínimos y máximos que puede tomar la solución, @Restnolineal es una función que retorna la restricción no lineal en términos de X, options permite ajustar las tolerancias del procedimiento matemático, el método de convergencia entre otra gran cantidad de opciones que tiene la solución del método. La matriz A y el vector B imponen las restricciones de desigualdad y las matrices Aeq y Beq las restricciones de igualdad (en los dos caso lineales), donde las restricciones se pueden escribir como:
En el caso del problema que compete al despacho óptimo la sintaxis con la cual se define el problema en f mincon se escribiría como:
Donde P es el vector de solución de potencias que dan el costo mínimo Cmin . A continuación se explican el planteamiento novedoso propuesto de las restricciones como extensión del trabajo presentado en 10.
2.1 Restricción de igualdad no lineal y modelación de pérdidas
Las pérdidas en las líneas pueden ser representadas como una función de la potencia generada mediante coeficientes de pérdidas de la siguiente manera:
donde Bmn , Bmo y B 00 conforman el conjunto de los coeficientes de pérdidas, que son matrices de dimensiones Ng x Ng , 1x Ng y 1x1 respectivamente, mientras que Pg es el vector columna de dimensión Ng x1 que contiene el valor de las potencias activas generadas.
De esta manera la restricción (4) se puede escribir como:
En el caso de plantas de generación renovable, estas se tratan como unidades que se despachan automáticamente, como si no tuviesen un costo asociado, entonces dejan de ser variables del sistema de ecuaciones y se edita la ecuación de restricción de potencia como:
donde Nr representa cualquier nodo con inyección de energías renovables. Nótese que el problema de despacho tendría Ng - Nr incógnitas para esta consideración. Esta ecuación es la que se escribe como @Losses según la ecuación (12) para la definición del problema en la sintaxis de f mincon.
2.2 Restricciones de magnitud de tensión
En esta parte, se muestra el procedimiento realizado para escribir las restricciones de la magnitud de las tensiones, y dejarla en la forma de la ecuación (11), es decir como restricción de desigualdad lineal. Para definir una relación entre los límites permitidos de operación de las magnitudes de las tensiones se buscó una relación entre la magnitud de las tensiones y la potencia generada. Para ello se usó la matriz C que se define como:
Se puede ver que la matriz C tiene dimensiones N x Ng .
La magnitud de las tensiones son una función diferenciable respecto a las potencias generadas, según se puede observar en los resultados del método incremental en 10, entonces los elementos de la matriz de derivadas parciales se pueden aproximar como:
con:
Se puede extender y reagrupar la representación de la ecuación 18 a forma matricial como:
Se puede ver que los valores de C , [|V
0
|] y  se pueden calcular para las condiciones iniciales de un caso base, que se calcula a partir de una simulación de un flujo de potencia inicial con una demanda esperada en los nodos PQ y una inyección probable de potencia por las fuentes renovables en los nodos PV. Luego son constantes todos los valores de la ecuación 19 , excepto los vectores [
|Vf |
] y
se pueden calcular para las condiciones iniciales de un caso base, que se calcula a partir de una simulación de un flujo de potencia inicial con una demanda esperada en los nodos PQ y una inyección probable de potencia por las fuentes renovables en los nodos PV. Luego son constantes todos los valores de la ecuación 19 , excepto los vectores [
|Vf |
] y  que son valores desconocidos porque no
que son valores desconocidos porque no
se sabe que valor van a tomar después de la optimización. A la ecuación 19 se le pueden atribuir las desigualdades:
y
Entonces para el caso de las magnitudes de tensiones máximas y mínimas se puede escribir la ecuación de restricción de desigualdad de la ecuación 4 como:
2.3 Restricciones de flujos máximos en las líneas
Se puede hacer una aproximación al cálculo de la magnitud del flujo de potencia de una línea entre dos nodos del sistema despreciando el valor de la admitancia shunt como:
Donde cada tensión representa los fasores en los nodos i y j, y el valor de Yij representa la admitancia equivalente de la rama serie del modelo de línea, así:
De esa manera se puede expandir la ecuación (24) para calcular la norma como:
Aplicando el teorema de Pitágoras se tiene:
Expandiendo los cuadrados y aplicando la identidad trigonométrica fundamental se llega a la ecuación:
Suponiendo que todas las tensiones están cercanas a la unidad, entonces se simplifica la ecuación a:
Finalmente se le aplica la raíz y si se supone que la diferencia angular entre las tensiones no es mayor a 30º entonces una aproximación por el primer término de la serie de Taylor permite escribir la ecuación como:
Se puede entonces escribir la ecuación en forma matricial para la magnitud de los flujos de potencia de las ramas del sistema como:
o:
Se debe tener cuenta que la matriz Yc tiene los signos de cada renglón establecidos suponiendo que el flujo de potencia real parte desde el nodo cuyo ángulo tiene el subíndice menor y llega hasta el de mayor, sin embargo si esto no es cierto se multiplica por menos el renglón correspondiente.
Las dimensiones de la matriz [Y c] dependen del número de ramas que hayan en el sistema, si hay R ramas entonces las dimensiones son RxN, para un sistema con N nodos y por lo tanto N ángulos. No se debe confundir esta matriz con la de admitancias.
Todo este procedimiento se ha realizado con el fin de poder obtener una relación entre las potencias activas generadas y los flujos entre las líneas. Como se ha obtenido una relación entre la matriz [ Sij ] y los ángulos de las tensiones, se puede relacionar estos últimos con la generación de las potencias por medio de la matriz A analizada en el método incremental presentado en 10:
De manera análoga al caso de la magnitud de las tensiones, los ángulos en función de las potencias generadas son una función diferenciable, que se puede aproximar con la matriz de incrementos de los ángulos como:
Y por lo tanto despejando para los ángulos finales se tiene:
Al igual que en el caso de la restricción de la magnitud de las tensiones, los vectores  y
y  se hallan para un caso base con potencias generadas y demandadas esperadas para la hora del día de análisis y por lo tanto son constantes.
se hallan para un caso base con potencias generadas y demandadas esperadas para la hora del día de análisis y por lo tanto son constantes.
Se puede entonces reemplazar la ecuación anterior en la ecuación 32 para obtener:
A diferencia de las tensiones en este caso solo se tienen restricciones por flujos máximos, por lo tanto se plantea la desigualdad:
Y por lo tanto la restricción de desigualdad se puede escribir en el formato de f mincon con:
2.4 Restricciones de potencia reactiva
Normalmente las fuentes de un sistema de potencia tienen límites de generación y consumo de potencia reactiva, por lo general se suele escribir esta restricción como:
Partiendo de la ecuación de potencia nodal:
Se puede despejar la potencia reactiva como:
Donde N es el número de nodos del sistema, θi , θk y δik son los ángulos de las tensiones Vi , Vk y del elemento Yik de la matriz de admitancias del sistema respectivamente.
Se puede definir para la potencia reactiva en un generador un incremento como:
Teniendo en cuenta que la variación de la potencia reactiva generada es más fuerte con respecto a la magnitud de las tensiones, se puede simplificar la expresión anterior si se supone una variación nula con los ángulos. Adicionalmente se puede recordar que el incremento de las tensiones se puede escribir en términos de las potencias generadas como:
En forma matricial se pueden combinar las dos últimas ecuaciones para obtener:
Donde M numera en este caso los nodos de generación, en forma simplificada se puede escribir la ecuación como:
En caso de no despreciar las variaciones de la potencia reactiva con los ángulos se obtendría la ecuación:
Donde A es la matriz de la ecuación 33. Las matrices con derivadas de la potencia reactiva respecto al ángulo y magnitudes se pueden hallar a partir de la ecuación 42.
Finalmente, para poder reescribir la restricción en el formato de f mincon
se expande como:
Factorizando y trasponiendo términos se tiene:
En la ecuación anterior el lado derecho de la ecuación será máximo en cada posición del vector resultante cuando Qf sea máximo, porque el resto de valores son constantes para un caso base, luego se puede escribir la restricción como:
Que sugiere calcular los valores de Aeq y Beq como:
Para potencias reactivas máximas y:
Para potencias reactivas mínimas.
2.5 Unión de restricciones
De acuerdo a las restricciones calculadas anteriormente se pueden reemplazar en la ecuación:
La matriz Aeqtotal y el vector Beqtotal total se puede definir incluyendo todas las restricciones si se realiza aumentan las matrices y los vectores como:
Es claro que el óptimo se calcula más rápido si se tienen en cuenta menos restricciones, entonces dependerá de las caracteristicas del sistema cuantas restricciones se deben tener en cuenta.
3 Resultados de simulación
Para la simulación se ha tomado como base el caso de Matpower de 8 nodos que tiene un bajo consumo de potencia, sin embargo debido a que la demanda es muy baja y las pérdidas no tienen mayor incidencia en el análisis se han editado las condiciones del caso incrementando la demanda, un esquemático del sistema se muestra en la siguiente figura.
En el sistema se tienen 8 nodos, 4 de generación y 4 de demanda, el sistema esta conectado a media tensión a un nivel 11.4kV. Se ha supuesto una demanda máxima de potencia en cada nodo de 2MW con factor de potencia de 0.9 en atraso y de acuerdo a estas condiciones se calcularon los conductores con ayuda de un simulador y se calculó la matriz de admitancia del sistema tomando como valores base 11.4kV de tensión y 1MVA de potencia. Las longitudes de las líneas se supusieron entre 3km y 10km siendo las más largas las provenientes del sistema y más cortas las asociadas a los generadores renovables. Se calcularon restricciones de flujo máximo a partir de la capacidad de corriente de los conductores y del nivel de tensión.
Por otro lado se tomaron como límites tensión entre 0.9 y 1.1 en por unidad, y los límites de potencia reactiva se dejaron de 1MVAR para las fuentes del sistema externo y de 0.5MVAR para las fuentes de energía renovable.
De acuerdo a estas condiciones se analizó:
Cuales son las probables potencias generadas por cada fuente renovable y fuente del sistema para algunas horas del día.
Como afecta usar un conjunto u otro de coeficientes de pérdida en el despacho.
Cuales son las probables pérdidas para algunas horas del día.
Como se diferencian los resultados de optimización con los del flujo óptimo de potencia de Matpower.
A que horas del día se espera que haya energía sobrante y almacenable en el sistema.
3.1 Variación de la potencia de las fuentes renovables
Para poder simular el comportamiento de la inyección de potencia debido a fuentes renovables, se obtuvieron curvas de velocidad y de radiación esperada para cada hora del día, teniendo como base las mediciones de UK environmental Change Network 21) y (22.
Para el presente trabajo se usó la ecuación de corrección de velocidad para una altura de 100m suponiendo que a esa altura se encuentran los aerogeneradores. De esa manera la curva de velocidad del viento esperada para cada hora del día se muestra en la Figura 2.
La varianza para algunas horas del día se calculó tomando un conjunto de muestras medidas en 3 meses y a partir de esos valores se estimaron los valores de α y de β que definen la forma de las curvas de densidad de probabilidad para una distribución de Weibull para la velocidad del viento 3. En la Figura 3 se pueden ver las curvas de probabilidad estimadas para 4 horas especificas del día.
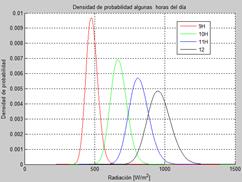
Por otra parte, en el caso de la radiación solar se utilizó una curva común de radiación esperada para cada hora del día y se supuso una varianza del 30% para cada una y de esa manera se encontraron los valores de µ y σ que
definen la curva de probabilidad Lognormal según 2. En las Figuras 4 y 5 se muestra la curva de radiación esperada y las densidades de probabilidad para algunas hora del día.
De acuerdo a estas curvas se han ajustado los valores de las potencias nominales de los aerogeneradores y las fotoceldas como se listan en la Tabla 1.
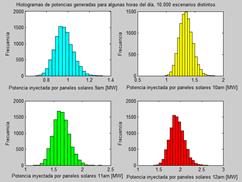
De esa manera se puede hacer un histograma con las potencias generadas debido a cada tecnología para cada hora del día, algunas de estas se muestran en las Figuras 6 y 7.
Se puede observar que la generación de potencia por los aerogeneradores es mas dispersa que la generada por los paneles solares, ambas tecnologías tienen inyección máxima a las 12 horas y si la demanda a esa hora del día no es lo suficientemente grande como para que se consuma instantáneamente la energía, es importante contar con un sistema de almacenamiento. En horas de la madrugada la inyección de potencia por parte de ambas tecnologías es muy baja debido a la ausencia de sol y que la velocidad del viento es baja.
3.2 Análisis de la energía sobrante
Para saber cual es la energía sobrante del sistema se define primero una curva de demanda para cada nodo PQ como se muestra en la Figura 8.
Se puede ver que al medio día donde hay máxima inyección de potencia por las fuentes renovables que suma alrededor de 4MW en los escenario más probables. La potencia demandada es a penas de 0.62MW, por ende
la de todos los nodos es de 2.48MW y se podría almacenar o inyectar a la red alrededor de 1.52MW, menos las pérdidas.
En la Figura 9 se muestra un histograma de potencia inyectable a la red sin tener en cuenta las pérdidas, es decir se registra la diferencia entre la potencia generada por fuentes renovables y la demandada solo si la primera supera la segunda. En estas condiciones se muestra el histograma de potencia inyectable al sistema por parte de las fuentes renovables.
En el presente trabajo no se considera un sistema con almacenamiento ni entrega de energía a la red, por lo tanto para evitar que haya energía sobrante se opta por subir la demanda de los nodos PQ para que a las 12 horas del día, que es cuando hay más energía sobrante toda la potencia sea consumida. Por ende se aumenta la demanda aparente diaria en un 15% en cada nodo.
3.3 Variación de la potencia generada por los nodos del Sistema
En esta sección se muestran los resultados de los óptimos obtenidos para cada escenario de generación, primero se analizan los despachos más probables de los generadores de la red para ciertas hora del día, es importante para tener presente la competencia que hay entre las dos fuentes del sistema los costos asociados a cada generador. Para este caso se supusieron que las funciones de costo de cada generador son:
Se puede ver que para este análisis se han suprimido los costos fijos de cada planta y solo se conserva el costo que varía con la generación.
Es de interés analizar los escenarios clave de acuerdo a la curva de demanda, y las generaciones esperadas, para horas con baja demanda como lo es antes de las 5h, se hizo un análisis de 100 muestras, recordando que a estas horas hay una inyección prácticamente nula de potencia por los paneles y las velocidades esperadas son del orden de 5m/s según se pudo ver en la Figura 3. En las Figuras 10 y 11 se pueden ver las posibles generaciones óptimas que obedecen a un costo mínimo total, de esa manera se puede ver que la variación se debe a que la inyección de energía por aerogeneradores es variable y por lo tanto el despacho de cada unidad también lo será. En estas condiciones sale beneficiado el generador 2 porque despacha mas potencia. Se puede ver que hay ligeras diferencias en el uso de los coeficientes, usando los coeficientes heurísticos se mantienen resultados similares a los incrementales y el runopf de Matpower, por otro lado los coeficientes de kron ofrecen un valor ligeramente mayor de la inyección en el generador 1. En el caso de la potencia del generador 2 se observan resultados más homogéneos a plena vista.
Si se analiza la hora con mayor inyección de potencia por las fuentes renovables como lo es las 12h se obtienen los histogramas de las Figuras 12 y 13.
Se puede ver que a esta hora del día la inyección por ambos generadores es muy baja, solo en unos pocos escenarios se genera para satisfacer la demanda restante, pero son cantidades bajas de potencia del orden de 0.6MW para el generador y 1MW para el generador 2. En general se puede ver que a esta hora se tiene una pobre participación de los generadores no renovables del sistema.
Por otro lado en el pico de demanda de las 14h, la distribución de generaciones se muestra en las Figuras 14 y 15, se puede ver que hay una gran tendencia de generar valores bajos de potencia para ambos generadores con cualquier conjunto de coeficientes. Los coeficientes de Kron favorecen en algunos escenarios al generador 2, a diferencia de los resultados obtenidos con los otros coeficientes de pérdida. Por otro lado se muestran resultados más parecidos en los despachos calculados con los coeficientes heurísticos, los incrementales y los obtenidos calculando con el runopf de Matpower.
Para horas posteriores a las 16 horas, la penetración de energías renovables empieza a decaer y por lo tanto pierde el sentido analizar los posibles despachos, debido a que ya será bastante predecible la demanda y los recursos de cada generador no renovable y no tendrá mayor influencia la inyección de energías de este tipo.
3.4 Análisis de pérdidas
En esta sección se analiza como varían las pérdidas para las mismas horas que se han venido analizando. En general se ha observado una discrepancia de los valores obtenidos calculando pérdidas con runopf , que se calculan con el resultado propio del flujo de potencia que se simula en la optimización, y los resultados obtenidos con las potencias solución obtenidas con f mincon. En este caso las pérdidas se calculan con los coeficientes de cada método que se obtuvieron para un caso base que tiene definida la potencia generada más probable y la demanda esperada. Las pérdidas se calculan con el vector de potencia que se obtiene de la optimización y los coeficientes del caso base como:
El método que calcula pérdidas con total certeza es el runopf porque la optimización implica la solución de un flujo de potencia.
Para las 5 horas se observa el histograma de la Figura 16, se puede ver que la forma de los histrogramas son diferentes en todos los casos, excepto en los incrementales y los heurísticos. Las pérdidas calculadas son de menor orden según los resultados del runopf y mayores en las calculadas por el método incremental. Se puede decir entonces que dependiendo del método elegido las pérdidas resultantes pueden ser mayores si se calculan por el método incremental y despachar con estos coeficientes puede ser inapropiado debido a que es indeseable que las pérdidas sean mayores.
Los histogramas de pérdidas a las 12h se pueden ver en la Figura 17, cuando hay más penetración de energía por fuentes renovable se puede observar que las pérdidas son mayores respecto a las 5 am porque crece la demanda, y se vuelve a ver que hay diferencia en la forma de los histogramas y los rangos de pérdidas probables. Nuevamente los coeficientes incrementales y heurísticos ofrecen pérdidas mayores respecto a los otros dos métodos.
A las 14 horas, Figura 18, se puede ver que hay una mayor dispersión en el cálculo de las pérdidas y nuevamente no se observa un patrón similar de los histogramas para los 4 métodos. Las pérdidas calculadas por los coeficientes de kron concentran el 70% de los resultados en el valor de 0.15MW. A diferencia de los otros casos, de nuevo en este caso los resultados obtenidos con los coeficientes incrementales y heurísticos ofrecen pérdidas ligeramente mayores a las calculadas por los otro métodos.
De acuerdo al lo expuesto anteriormente, se hicieron 100 escenarios de posibles generaciones para las fuentes no convencionales y se simularon los óptimos sin restricción de desigualdad.
4 Conclusión
Se encontraron resultados de despachos bastante similares a los obtenidos con el flujo de potencia óptimo de Matpower, en las diferentes horas de análisis, con la ventaja de que el método utilizado respecto al de Matpower se ahorra el tiempo de simular el flujo de potencia final. Aunque estos tiempos no son apreciables para sistemas como el que se analizó si puede ser significativo cuando se analicen sistemas con mayor penetración de energías renovables o con más nodos.
Se pudo ver que los coeficientes obtenidos mediante la optimización heurística presentaron resultados más cercanos a los del runopf , seguidos por los coeficientes incrementales. Los coeficientes deben dar resultados concordantes entre sí, porque sino podrían estar favoreciendo a algún generador, por ejemplo en el despacho realizado con los coeficientes de Kron a diferencia de los otros tres resultados da generaciones hasta de 3MW para el generador 2 a las 14h, apuntando a que sería erróneo calcular el despacho con estos coeficientes a esta hora del día.
Es importante tener en cuenta que siempre que haya energía renovable sobrante en el sistema, se le debe atribuir un costo a esta energía con el fin de que entre a disputar con las fuentes de otro tipo en el despacho económico. Aunque en el presente escrito no se abarco ese tema, a medida que se hace significativo el aporte de estas fuentes, en necesario considerar el costo por unidad de potencia disponible.
La desventaja del método es que se deben disponer previamente de un conjunto de coeficientes, por ende si requiere de la simulación de un flujo de potencia previo a la optimización. Sin embargo si se usan los coeficientes estimados con el método de DEEPSO, es posible que solo se deban calcular una vez, debido a que son robustos ante cambios de generación y demanda. Por otro las ecuaciones de desigualdad de las restricciones se calcularían solo una vez, y después si se podrían hacer los análisis de Montecarlo, mientras que con runopf se requeriría un flujo óptimo para cada iteración del análisis.