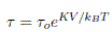1 Introducción
Si bien, el estudio de nanopartículas magnéticas (NPM) se ha enfocado en su síntesis y en la optimización de sus propiedades para mejorar elementos magnetoresistivos 1),(2, establecer la spintronica como nueva tecnología 3, para reemplazar líquidos de enfriamiento en transformadores de potencia eléctricos 4 o para aprovechar su afinidad superficial y usarlas en remediación ambiental, 5, en los últimos años se han abordado estudios sobre las aplicaciones de nanopartículas en medicina para el tratamiento y diagnósitico del cáncer, y han sido las nanopartículas óxidos de hierro (magnetita Fe3O4, maghemita γ- Fe2O3) las que han tomado gran importancia en este tipo de aplicaciones, ya sea transportando fármacos 6, mejorando la calidad de imágenes médicas de diagnóstico 7, o usándose en procedimientos de teranostico: usos combinados tanto para terapia, detección y diagnóstico del cáncer 8),(9.
La primera vez que se propuso la utilidad de los óxidos de hierro como agentes terapeúticos contra el cáncer fue en 1957. En este año, Gilchrist 10, propone que los óxidos de hierro pueden ser utilizados como agentes reductores de células tumorales. En esa investigación se realizó un estudio post-mortem de tejido tumoral y se logró la reducción de la metástasis en el nodo linfático después de inyectarle una dosis de partículas magnéticas de tamaño micrométrico de γ- Fe2O3 en suspensión acuosa y someter al tumor a un campo de radiofrecuencia (RF). Si bien, su investigación no prosperó, no fue si no hasta inicios del siglo XXI donde se retomo esta aplicación y se estudio a fondo esta problemática, desde la física, la química y la biología y actualmente la medicina.
La terapia de reducción de tejido tumoral usando NPM y campos RF, se conoce como hipertermia magnética (HM) y se fundamenta en la capacidad de las NPM de absorber energía del campo magnético y transmitirla al medio en forma de calor. La propiedad de las NPM que sirve como parámetro de mérito para determinar cuanta energía electromagnética se transformó en calor se denomina SAR o disipación de calor (SAR por las siglas en inglés de Specific Absorption Rate) 11 y se puede inferir a partir del aumento de temperatura de una suspensión de nanopartículas magnéticas en un campo de radiofrecuencia. A este parámetro también se le suele llamar potencia específica disipada o SLP por sus siglas en inglés.
Actualmente, el tamaño de partícula se ha reducido hasta la nanoescala (diámetros entre 10 y 20 nm) y se busca la optimización de sus propiedades a partir de los procesos de síntesis, en especial las propiedades que afectan de manera directa a su capacidad de transformar la energía magnética en calor tales como tamaño, distribución de tamaño, estructura cristalina, funcionalización superficial y momento magnético y también para encontrar nuevas aplicaciones12.
Los procesos de generación de calor en las NPM a partir de campos electromagnéticos son bien conocidos, tanto teórica 11),(13),(14 como experimentalmente 15),(16),(17, pero la concordancia entre las observaciones experimentales y las predicciones teóricas no son muy buenas 15),(18),(19. Esto se debe principalmente a que las NPM están en un entorno altamente interactuante, es decir, una partícula está sometida a interacciones de carácter repulsivo, como la electrostática y la estérica, e interacciones de carácter atractivo, como la la de London-van der Waals. Estas interacciones conllevan a la formación de agregados de NPM donde la interacción magnética dipolar se maximiza lo cual causa que la energía interna de cada partícula se modifique y por lo tanto se afecte su SAR 20),(21, estos efectos se visualizan principalmente en la modificación del tiempo de relajación magnética de las partículas 22),(23),(24.
Si bien, el modelado teórico predice comportamientos del SAR en función de las interacciones dipolares, moduladas por la concentración de NPM en la suspensión, que han sido recientemente confirmados experimentalmente 18),(25, obtener a partir de estos modelos el valor numérico del SAR aún es materia pendiente, una forma de resolver este problema es considerando una energía de activación magnética (o energía de barrera) efectiva, determinada a partir de medidas magnéticas bajo campos estáticos (midiendo la coercitividad en función de la temperatura) o bajo campos dinámicos (midiendo la susceptibilidad magnética en función de la temperatura) 23.
Aunque el entendimiento, desde el punto de vista físico sobre como influyen las propiedades de las NPM, y del medio en el cual se encuentran dispersadas, en el SAR, aún no está completo, desde el punto de vista médico ya existe un gran avance en la aplicación de NPM de óxidos de hierro, principalmente magnetita, en el tratamiento del cáncer por hipertermia magnética. El establecimiento de la HM como terapia clínica se debe a que es un tratamiento que no presenta mayores efectos secundarios, tales como los causado por las terapias radiactivas (quimioterapia y radioterapia), se basa en la premisa de que las células cancerígenas tienen una resistencia menor a cambios de temperatura que las células sanas, lo cual hace a la HM una terapia selectiva26),(27 y que las nanopartículas de óxidos de hierro son fáciles de metabolizar en el hígado 28),(29, además son los únicos materiales aprobados por la agencia estadounidense Food and Drugs Administration para su aplicación en ensayos con humanos 26.
Estas ventajas han llevado a la creación de MagForce en Alemania, una empresa tecnológica dedicada al desarrollo de la nanomedicina, donde se han desarrollado aplicaciones clínicas exitosas de la HM en personas con cáncer de páncreas (7 pacientes), esófago (10 pacientes), próstata (29 pacientes) y glioblastoma multiforme (80 pacientes) 30),(31, además existen reportes fuera de MagForce en los cuales se reporta éxito en el tratamiento por HM de pacientes con neoplasia cérvica intraepitelial 32. Otra parte de la investigación se ha enfocado en la aplicación de multi-terapias, ya sea para potenciar el efecto de la HM y disminuir los efectos secundarios de los tratamientos radiológicos 33, o para potenciar el efecto y uso de nuevas terapias tales como la terapia fototérmica 34.
Este trabajo presenta un breve marco teórico y experimental,que debe tenerse en cuenta para el estudio y aplicaciones de NPM de óxidos de hierro en el tratamiento de hipertermia magnética. Para ampliar la discusión sobre algunos puntos de importancia, se ha dividido este documento en dos partes, en la primera parte, que corresponde al presente manuscrito, se remarcan las principales propiedades de las NPM que influyen en la disipación de calor, y cuales son las leyes físicas que los gobiernan; en una siguiente entrega de esta revista, se tratarán temas corcenientes a los principales procedimientos de síntesis, técnicas de caracterización de NPM, y medidas experimentales de disipación de calor y su modelado con los modelos expuestos en el presente artículo.
2 Nanopartículas magnéticas monodominio
Se denomina nanopartícula magnética a aquella entidad física cuyo tamaño se encuentra en la nanoescala y posee un momento magnético neto (µ) cuya magnitud es miles de veces el valor del magneton de Bohr, siendo µB = 9.27 x 10 − 24 Am 2, la unidad de momento magnético atómico 29),(35. Las mismas están compuestas por un material que en su estado "bulk"puede ser ferro o ferrimagnético. En el caso de la magnetita y la maghemita, presentan un comportamiento ferrimagnético con 4 µB por fórmula unidad para la magnetita y 2.5 µB para la maghemita, 36.
Un material en bulk, está formado por dominios magnéticos, zonas del material en las cuales existe una alineación de los momentos magnéticos atómicos, los mismos se forman para minimizar la energía de magnetostática dentro del material. A medida que se reduce el tamaño del material, la energía necesaria para rotar los espines atómicos del material es mayor que la necesaria para mover la pared de dominio, lo cual provoca un aumento en la coercitivad del material, el cual tiene un máximo cuando se acerca a el valor de la energía de anisotropía magnética, la cual determina la barrera de energia que debe superar un momento magnético para cambiar de dirección37.
Cuando el tamaño se reduce un poco mas, generalmente por debajo de los 10 nm para NPM de magnetita, la energía de anisotropía domina sobre la energia magnética y las paredes de dominio desaparecen del material y los momentos magnéticos atómicos están todos alineados en un solo dominio,
38 formando así una nanopartícula magnética monodominio.
El comportamiento magnético colectivo de un grupo de NPM monodominio depende de la temperatura a la cual se encuentre el sistema y de su estado de agregación. Para un sistema compuesto por N NPM monodomio no interactuantes (no hay efecto de la interacción dipolar magnética) en ausencia de campo magnético, si la energía térmica es mayor a la energía de anisotropía magnética, los momentos magnéticos individuales tienden a orientarse de forma aleatoria. A medida que la energía térmica disminuye y la energía de anisotropía magnética se vuelve dominante, aparece un ordenamiento de los momentos magnéticos y aparece una magnetización diferente de cero cuyo valor aumenta a medida que la temperatura disminuye.
Esta temperatura a la cual se da este cambio se conoce como temperatura de bloqueo ( Tb ), la cual depende del volumen de la partícula (V ), la constante de anisotropía magnética o densidad de energía de anisotropía (K) y de un parámetro externo, el tiempo de medida de la técnica con la cual se está determinando la magnetización del sistema ( τm ). Conocer el tiempo de medida de la técnica usada es de importancia puesto que si el tiempo de relajación de la NPM (τ ) es mayor que τm , el sistema se observará como “desbloqueado”, en el caso contrario, se dice que el sistema esta “bloqueado” puesto que el momento magnético se observa invariante y no hay una variación de su orientación durante un ciclo de medida 39.
Cuando la temperatura se acerca al cero absoluto, el sistema se encuentra totalmente bloqueado y la única forma de superar la barrera de energía es aplicando un campo magnético, cuando la energía de este campo es igual a la energía de la barrera, se produce la orientación del momento magnético en la dirección del campo, esto sucede cuando la intensidad del campo aplicado es igual al campo de anisotropía de la NPM ( Hk ), este modelo se conoce como modelo de Stoner-Wohlfarth 40. En este caso, la coercitividad del sistema es igual a Hk , y disminuye a medida que aumenta la temperatura hasta alcanzar un valor nulo cuando se alcanza la temperatura de bloqueo.
Dicho esto, un sistema de NPM monodominio que se encuentra por encima de Tb , tiene una magnetización nula en ausencia de campo, a medida que se aumenta la intensidad del campo aplicado, se genera una alineación de los momentos magnéticos en la dirección del campo aplicado, si la intensidad del campo es mucho menor que Hk , la magnetización del sistema responde de forma lineal con la intensidad del campo aplicado, lo cual se conoce como teoría de respuesta lineal 41. Cuando el campo es mucho mayor que Hk todos los momentos magnéticos se alinean con el campo y se obtiene la magnetización de saturación del sistema ( Ms ). Este fenómeno se conoce como superparamagnetismo, puesto que se asemeja al paramagnetismo atómico pero a una escala mucho mayor debido a los valores que toman los momentos magnéticos de las NPM.
Así, el superparamagnetismo se da por una respuesta colectiva de los momentos magnéticos de las partículas, las cuales, en el caso de los óxidos de hierro, presentan una alineación ferrimagnética en su interior, y está determinado por el tiempo de medida de la técnica de caracterización magnética.
A continuación se amplía la discusión sobre algunos de los puntos nombrados anteriormente.
3 Energía de anisotropía y mecanismos de relajación magnética
Usualmente, las propiedades de las partículas monodominio no son completamente isotrópicas, contribuciones anisótropas asociadas a la forma, esfuerzos internos o estructura cristalina deben ser consideradas 40),(42. Si la partícula presenta anisotropía uniaxial se genera un eje fácil de magnetización o eje de anisotropía a lo largo de la misma.
En ausencia de fluctuaciones térmicas, si el momento magnético de la NPM forma un ángulo φ con el eje de fácil magnetización, la energía de anisotropía magnetocristalina ( EK )de una NPM de volumen V está dado por la ecuación (1).
Donde K es la constante de anisotropía magnética. El modelo predice dos estados de mínima energía separados por una barrera de potencial igual a ∆E tal como se esquematiza en la Figura 1.

Figura 1: Representación esquemática de los niveles de energía de una NPM teniendo en cuenta su energía de anisotropía magnética. (a) En ausencia de campo magnético. (b) En presencia de campo magnético
Los momentos magnéticos que están en el estado 1 deben adquirir una energía igual a ∆E para pasar al estado 2. Cuando se aplica un pequeño campo magnético, la altura de la barrera se modifica de forma que ∆E = KV (1 + h)2.
donde h = µoH/KV , es el campo reducido. Como ya se dijo anteriormente, el campo aplicado necesario para superar la barrera de energía se conoce como campo de anisotropía Hk y está dado por la ecuación (2).
En la ecuación (2), Ms = µ/V es la magnetización de saturación de la NPM. De esta forma, la energía de la barrera para T = 0K es:
A medida que se aumenta la temperatura, los efectos térmicos tienen lugar y la energía de la barrera cambia debido a las fluctuaciones térmicas en la dirección del vector µ, de esta forma, la variación de la barrera de energía debido a la temperatura está dada por la ecuación (4)
Donde τ es el tiempo en el cual la NPM permanece en uno de los estados de menor energía y τo se conoce como el tiempo característico (aprox. 10-9- 10-10s). Si solo se consideran contribuciones de la anisotropía magnética a la barrera de energía, se tiene que el tiempo de relajación es:
La inversa de a ecuación (5) inversa representa la probabilidad de salto por unidad de tiempo entre un estado y el otro, este proceso se conoce como relajación de Néel y tiene asociado un tiempo de relajación τN .
Como se dijo anteriormente, para un proceso térmicamente activado, la temperatura para la cual τ = τm , se conoce como temperatura de bloqueo Tb , así que de la ecuación (4) se obtiene que:
De esta forma, las ecuaciones (3) y (4), representan las energía de la barrera, siendo el valor determinado por la ecuación (3) el valor máximo de la barrera (para T = 0K) y la ecuación (4) determina la variación de la altura de la barrera con la temperatura. Tal como se dijo anteriormente, en el modelo de Stoner-Wohlfarth, la coercitividad tiene su máximo valor ( Hk ) cuando T = 0 y disminuye a medida que aumenta la temperatura, es así como a partir de las ecuaciones (3) y (4) se obtiene un modelo de la variación del campo coercitivo con la temperatura dada por la ecuación (7):
El tiempo de medida τm depedende de la técnica de medida, por lo tanto la Tb observada varía según la técnica utilizada, así para medidas de suscpetibilidad a.c el tiempo de medida es el inverso de la frecuencia que se utiliza para la medida ( τm = 1/ω, 10 Hz<ω<10000 Hz) 24, para la técnica de magnetrometría por SQUID τm = 100 s 15, para la técnica de espectroscopía Mossbauer τm = 1 /fL , donde fL es la frecuencia de Larmor ( fL = 0.3 × 10 − 8 Hz 57 F e) 43.
Por otro lado, si la partícula posee un grado de libertad rotacional, la dirección de su momento magnético cambiara dependiendo de las interacciones entre la NPM y el medio en el cual se encuentre, este mecanismo se conoce como relajación de Brown. Si la viscosidad del medio es η y la partícula tiene un volumen hidrodinámico VH , el tiempo de relajación de Brown ( τB ) en el cual el momento magnético se encuentra en determinada dirección está dado por la ecuación (8):
De esta forma, existen dos mecanismos de relajación, y el mecanismo con el menor tiempo es el dominante, mientras que el tiempo de relajación total está dado por la ecuación (9):
4 Influencia de las interacciones dipolares en el tiempo de relajación
En un sistema real, cada nanopartícula está rodeada por otras NPM, las cuales afectan su mecanismo de relajación magnética. Si consideramos la interacción de tipo dipolar magnético, la barrera de energía definida en la Figura 1 se ve afectada de la forma representada en la ecuación (10) por la energía de campo medio (∆ Eint ) producida por el entorno.
En 1988, Dormann, Bessais y Fiorani (DBF)24 determinaron analíticamente el tiempo de relajación modificado por las interacciones, considerando que la barrera de energía de la i-ésima partícula se ve afectada por el campo dipolar generado por el momento magnético de la j-ésima partícula, separadas cierta distancia L y extendiendo la suma a todas las partículas vecinas (n). Así, se propone una constante de anisotropía, de la forma propuesta en la ecuación (11), y un tiempo característico, dado por la ecuación (12), que tienen en cuenta el efecto de las interacciones dipolares.
Donde b 1 = V (3 cos2 θ 1)/L 3 es un término proporcional a la energía dipolar magnética, siendo θ el ángulo formado entre dos momentos magnéticos, y n 1 es el número de primeros vecinos.
A partir del modelo DBS se puede concluir que las interacciones dipolares aumentan la barrera de energía, puesto que la constante de anisotropía aumenta.
Por otro lado, en 2014, Landi 13, considerando un modelo de campo medio, realizó cálculos numéricos para incluir las interacciones dipolares en la ecuación de Fokker-Planck, que describe la evolución temporal del sistema. Para un sistema monodisperso la intensidad de las interacciones dipolares depende de la concentración de NPM en el coloide. Incrementando la concentración desde un estado infinitamente diluido, primero se observan cambios en el tiempo de relajación, relacionados con la barrera de energía, seguidos por la aparición de un grado de orientación de los momentos magnéticos y finalmente un estado ordenado con magnetización no nula incluso en ausencia de campos externos.
De esta forma el modelo propone que la barrera de energía efectiva que está dada por la ecuación (13):
Donde p 2 0.9 es el promedio de las proyecciones del momento magnético de la partícula sobre la dirección preferencial de la magnetización dada por el campo dipolar, (promedio del polinomio de Legendre de orden dos) y γ es un parámetro proporcional a la energía de interacción dipolar dado por 14
Este modelo teórico ha sido recientemente confirmado experimentalmente por diferentes autores 15),(25),(44.
5 Procesos de magnetización
Un sistema de NPM no interactuantes tendrá una magnetización nula en ausencia de campo magnético, debido a que las fluctuaciones térmicas producen que cada momento magnético esté aleatoriamente orientado. Al aplicar un pequeño campo  se inducirá la alineación del momento magnético
se inducirá la alineación del momento magnético
de algunas partículas en la dirección del mismo.
Para una partícula monodominio con momento magnético  sobre la cual se aplica un campo magnético externo
sobre la cual se aplica un campo magnético externo  , la magnetización M del sistema paralela al campo magnético (45) será:
, la magnetización M del sistema paralela al campo magnético (45) será:
donde L(ξ) es la función de Langevin cuyo argumento es ξ = µµoH / kBT y µo es la permeabilidad del vacio. De acuerdo a la teoría de respuesta lineal, para bajas intensidades de H se pude escribir M = χoH , y a partir de la ecuación (14) se puede obtener que:
Para aplicaciones de estas NPM en hipertermia magnética es necesaria la aplicación de un campo magnético a.c en el rango de la radiofrecuencia.
Si este campo es de la forma H(t) = Hoeiωt donde ω=2πf siendo f la frecuencia de oscilación del campo magnético y Ho es la amplitud del mismo. De esta forma, se tiene para pequeños valores de Ho la magnetización es
Puesto que χ = χ’ - iχ’’ , donde χ’ es la componente en fase de la susceptibilidad y χjj es la componente fuera de fase. χ'’ está retrasada con respecto al campo de excitación, esta componente determina la capacidad de absorber energía y es la única que contribuye al aumento de la energia interna ∆U de la partícula 46),(47),(48 y se puede escribir de la siguiente forma:
Siendo τ el tiempo de relajación de la NPM. (18)
6 Disipación de calor en campos de radiofrecuencia
Una forma de cuantificar la cantidad de energía del campo RF transformada en calor por las NPM, es por medio de la velocidad específica de absorción de potencia (SAR). Esto se puede hacer utilizando la termodinámica y la respuesta de la magnetización de las NPM a campos magnéticos alternos. El trabajo realizado para magnetizar la nanopartícula es  donde
donde  es el vector de inducción magnética. De la primera ley de la termodinámica, considerando un sistema adiabático, el cambio en la energía interna es dU =dW y se puede escribir como se presenta en la ecuación (19):
es el vector de inducción magnética. De la primera ley de la termodinámica, considerando un sistema adiabático, el cambio en la energía interna es dU =dW y se puede escribir como se presenta en la ecuación (19):
Así la cantidad específica de energía que una NPM puede transformar en calor es SAR=f ∆U .
Con esto en mente, se puede calcular el SAR producido por un grupo de NPM con polidispersidad de tamaño definida por una función de distribución gN (r) con una única ecuación 49),(50, que tenga en cuenta tanto los parámetros del campo RF como las propiedades magnéticas de las NPM además de las interacciones de tipo dipolar entre las mismas:
De esta forma, conociendo algunas propiedades de las NPM es posible, usando la ecuación (20) predecir la cantidad de calor disipada por un sistema de NPM.
7 Conclusiones
El estudio de nanopartículas magnéticas de óxidos de hierro y la posibilidad de aplicarlas en hipertermia magnética es posible debido a su biocompatibilidad y sus propiedades físicas y químicas que son optimizadas en la nanoescala. Para mejorar la capacidad de transformar la energía electromagnética en energía térmica, es necesario entender desde el punto de vista físico, cuales son las propiedades que están afectando esta capacidad, por lo tanto, y después de una exhaustiva caracterización magnética, y estructural tanto de las partículas individuales como de su comportamiento colectivo, es posible determinar su aplicabilidad en hipertermia magnética. Es así como con una correcta aplicación de los modelos físicos es posible predecir el comportamiento de un sistema de NPM.
En esta primera parte, se han dado ciertas pautas que se deben tener en cuenta para el estudio de nanopartículas magnéticas. Los modelos presentados se pueden utilizar para determinar de forma general las propiedades de las NPM. Su uso en el modelado de la respuesta de las NPM ante un campo de radiofrecuencia es de gran importancia sobre todo cuando se desea aplicar estos sistemas en una terapia oncológica tal como la hipertermia magnética, por lo tanto este tema se tratará en la segunda parte de esta revisión.