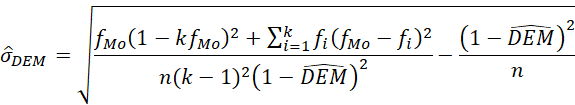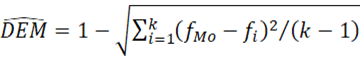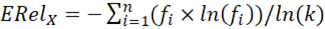Introducción
Medidas de variación para datos en escala nominal
Las escalas de medición nominales que constituyen sistemas de clasificación de los elementos de una población son muy frecuentes en la investigación en ciencias sociales y de la salud (Allanson & Notar, 2020), entre las que se encuentra la psicología (Guyon, Kop, Juhel, & Falissard, 2018). Para su descripción se tienen las tablas de frecuencias y diversos gráficos, como el diagrama de barras y la gráfica de sectores (Pallant, 2020). A su vez, está bien establecido que la moda es la medida de tendencia central adecuada para estas variables (Aspers & Corte, 2019). Cabe preguntarse si existen estadísticos descriptivos para medir la variabilidad de los datos cualitativos.
La respuesta es sí, aunque en algunas aulas de psicología se puede escuchar por parte del docente que no. De hecho, se han definido muchas medidas de variación para variables cualitativas (Agresti & Agresti, 1978; Kvalseth, 2011; Wilcox, 1973) y aun así son poco conocidas, usadas y estudiadas. Tal es el caso que, en muchos manuales de estadística básica o aplicada, no se las menciona, y los paquetes estadísticos no las incluyen (Agresti, 2019; Mangiafico, 2016; Zaiontz, 2022; Venables, Smith, & the R Core Team, 2021). No obstante, cabe señalar que su desarrollo es relativamente reciente. Parten de mediados del siglo xx con la publicación del artículo del matemático estadounidense Claude Elwood Shannon (1916-2001) sobre la teoría matemática de la comunicación, proliferan durante las décadas de 1960 y 1970 (Agresti & Agresti, 1978) y, en la actualidad, se siguen desarrollando (Evren & Erhan, 2017; Weiss, 2019). Dentro de las ciencias sociales, se usan sobre todo en sociología y economía política (Weiss, 2019; Wilcox, 1973).
Entre estas medidas, se pueden destacar el índice de variación cualitativa (IVC) de Gibbs y Poston (1975), la razón de variación (RV) de Freeman (1965), la razón de variación de la moda (RVMod) de Wilcox (1973), la desviación estándar desde la moda (DEM) de Kvalseth (1988) y el índice de entropía relativa (ERel) de Shannon (1948). Además, en el presente artículo, se propone una nueva medida a partir de la razón de variación de Freeman (1965), a la cual se denomina razón de variación universal (RVU), ya que se puede aplicar con cualquier tipo de distribución. Se trata de una medida muy sencilla de cálculo que supera las limitaciones de los índices de Freeman (1965) y Wilcox (1973) y parece medir de forma muy adecuada la variabilidad de la frecuencia entre las categorías cualitativas.
Todas estas medidas se usan preferentemente con variables cualitativas. Su aplicación con variables de categorías ordenadas (ordinales) y variables cuantitativas discretas es posible, pero se desaconseja por una infrautilización de la información contenida en los datos frente a las medidas absolutas o relativas basadas en distancias entre cuantiles o basadas en el promedio o la mediana de puntuaciones diferenciales con respecto a la media aritmética o la mediana. Los índices de Freeman (1965), Wilcox (1973), Gibbs y Poston (1975), Kvalseth (1988), así como el nuevo índice propuesto (RVU), basados en la moda, se desaconsejan totalmente para muestras de variables cuantitativas continuas, ya que la moda como medida de tendencia central puede ser inexacta con estos datos muestrales, aparte de infrautilizar la información contenida en los mismos. No obstante, con una distribución continua (datos poblacionales), si su función de densidad tiene un pico definido (moda poblacional), es factible el cálculo de estas medidas de variación, pero no aconsejable. El cálculo del índice de variación cualitativa y la entropía relativa con muestras de variables cuantitativas continuas requiere definir un número específico de categorías, esto es, discretizar o definir k intervalos de clase, lo que incrementa más la pérdida de información aunado al hecho de ignorar la naturaleza cuantitativa de los datos muestrales; de ahí su contraindicación. Con la función de densidad de una distribución continua, la información de Shannon se puede calcular directamente usando integrales, lo que es una práctica común (Al-Omari, 2016; Amigó, Balogh, & Hernández, 2018). También con algunas funciones continuas se puede determinar la entropía máxima y obtener la entropía relativa a través del cociente entre la entropía y su máximo (Nielsen & Nock, 2017).
Una característica que comparten todas estas medidas de variación para variables cualitativas es poseer un rango de 0 a 1. En este rango, el valor de 0 corresponde a la distribución de una variable constante, en la que un valor concentra toda la probabilidad a nivel poblacional o toda la frecuencia a nivel muestral. El valor de 1 corresponde a una distribución uniforme, en la que todos sus valores tienen la misma probabilidad a nivel poblacional o la misma frecuencia a nivel muestral. El valor varía de una medida a otra. Unas son más sensibles a la presencia de una moda muy definida y se aproximan rápidamente a 0, como la razón de variación de Freeman (1965). Por el contrario, otras son más sensibles a una distribución uniforme con probabilidades o frecuencias homogéneas entre sus categorías cualitativas y convergen rápidamente a 1, como el índice de variación cualitativa de Gibbs y Poston (1975).
Definición de cinco medidas de variación para datos nominales
Entropía relativa
La entropía es la medida del desorden en un sistema de elementos (Sharp, 2019). La entropía en la teoría de la probabilidad es máxima cuando todos los elementos son equiprobables y la presencia de unos elementos no permiten predecir la aparición de otros. El origen del concepto procede de la termodinámica, fue aplicado a la teoría de la información por Claude Elwood Shannon (1948) y de ahí pasó a la estadística como una propiedad para caracterizar distribuciones tanto discretas como continuas y medir la variabilidad en variables cualitativas (sistemas de clasificación). A nivel poblacional se denota con la letra griega mayúscula eta (Η) y a nivel muestral con la letra latina mayúscula E. La entropía es la esperanza matemática de la información de Shannon (1948) o logaritmo de la probabilidad del valor de una distribución:  .
.
Cuando la información (I
X
) está en base 2 ( ), se habla de bits o unidades binarias de información. Cuando la información está en base decimal (
), se habla de bits o unidades binarias de información. Cuando la información está en base decimal ( ), se habla de dits o unidades decimales de información. Cuando la información está en base natural (
), se habla de dits o unidades decimales de información. Cuando la información está en base natural ( ), se habla de nepits o unidades neperianas de información. En la teoría de probabilidad, usualmente, se toma base e, esto es, logaritmo neperiano (ln).
), se habla de nepits o unidades neperianas de información. En la teoría de probabilidad, usualmente, se toma base e, esto es, logaritmo neperiano (ln).
Al conocerse el valor máximo de la entropía en una distribución discreta: ln(k), que corresponde a la distribución uniforme discreta, se puede calcular la entropía normalizada o relativa de Shannon. La entropía relativa se denota con ΗRel a nivel poblacional y ERel a nivel muestral, y es la entropía dividida por su valor máximo (Shannon, 1948). Para una distribución de frecuencias empíricas o muestrales, la entropía se calcula del siguiente modo:
Sea una muestra aleatoria de tamaño n de una variable cualitativa X con k categorías nominales. Se denota con n i a la frecuencia absoluta y f i = n i / n a la frecuencia relativa de cada categoría nominal (i = 1, 2, ... k).
En el caso de una variable aleatoria constante, al número de categorías (k) se le da un valor de 2 (a y no a), para el estadístico ERel puede tomar valores en el intervalo [0, 1].
Razón de variación
La razón de variación (RV) de Freeman (1965) parte de una fórmula de variación en torno a la moda y su expresión se simplifica al complemento de la frecuencia modal, por lo que, finalmente, usa una información mínima de la distribución. No obstante, la ventaja de este estadístico es su facilidad de cálculo.
Sea una muestra aleatoria de tamaño n de una variable cualitativa X con k categorías nominales. En esta muestra, aparece una moda (Mo) o categoría con frecuencia máxima que es única y tiene una frecuencia absoluta  y relativa f
Mo
.
y relativa f
Mo
.
Razón de variación de la moda
Wilcox (1973) desarrolló una razón de variación estandarizada basada en la moda que se puede expresar en función de la de Freeman (1965) y siempre toma un valor mayor o igual que la de Freeman. Frente a RV, añade a la frecuencia modal la información sobre el número de categorías cualitativas.
Al igual que la razón de variación de Freeman (1965), la RVMod de Wilcox (1973) está acotada de 0 a 1. Precisamente, se trata del complemento de una proporción.
Requiere necesariamente que la distribución sea unimodal. En caso de una distribución uniforme, no se puede dar a la frecuencia modal un valor de 0, como se argumentó con la razón de variación de Freeman (1965), ya que el estadístico RVMod queda fuera del rango de 0 a 1 estipulado para los índices de variación estandarizados de variables cualitativas (Wilcox, 1973). Consecuentemente, tiene más limitaciones que la razón de variación de Freeman.
Índice de variación cualitativa
Gibbs y Poston (1975) propusieron un índice estandarizado denominado índice de variación cualitativa (IVC). Es la medida de variación cualitativa más usada, sobre todo en ciencias sociales (Kvalseth, 1988). Tiene la ventaja de usar toda la información de la frecuencia, aparte del número de categorías cualitativas y se puede calcular con cualquier tipo de distribución para datos cualitativos.
En el caso de una variable constante, es decir, que tiene un único valor, el índice de variación cualitativa (ICV) es 0.
En el caso de una distribución uniforme, el valor de ICV es 1.
Desviación estándar desde la moda
La desviación estándar desde la moda (DEM) de Kvalseth (1988) se define como el complemento de la raíz cuadrada del promedio del cuadrado de unas puntuaciones diferenciales. Son las diferencias entre la frecuencia modal y el resto de las frecuencias, por lo que este promedio varía de 0 a 1. El valor de DEM es menor o igual que el índice de Wilcox (1973).
Frente a RV y RVMod, la ventaja de la DEM es que usa todas las frecuencias y se puede calcular con modas múltiples, incluso con una distribución uniforme, como el índice de Gibbs y Poston (1975). Aparte, permite definir un error asintótico ( ) y hacer estimaciones por intervalo con muestras grandes.
) y hacer estimaciones por intervalo con muestras grandes.
 = cuantil de orden 1−(α/2) de una distribución normal estándar N (0,1). Para un valor de α de .05, Z
.975
corresponde a 1.96.
= cuantil de orden 1−(α/2) de una distribución normal estándar N (0,1). Para un valor de α de .05, Z
.975
corresponde a 1.96.
El presente estudio tiene como primer objetivo proponer una modificación de la razón de variación para superar las limitaciones de las fórmulas desarrolladas por Freeman (1965) y Wilcox (1973). Su segundo objetivo es describir el patrón de comportamiento de las tres razones de variación, la entropía relativa de Shannon (1948), el índice de variación cualitativa de Gibbs y Poston (1975) y la desviación estándar desde la moda de Kvalseth (1988), aplicando estos seis índices de variación a tablas de frecuencias correspondientes a distintos tipos de distribuciones de datos nominales y, de este modo, observar si existe alguna regularidad y si el nuevo índice propuesto es adecuado.
Método
Participantes o Muestra
El presente estudio está basado en unos datos generados para observar y comparar el comportamiento de los índices con distintas distribuciones.
Procedimiento
Para el primer objetivo de proponer una modificación de la razón de variación, se realizan argumentaciones y pequeñas demostraciones algebraicas. A este nuevo índice se denomina razón de variación universal, ya que se pretende que sea válido para cualquier tipo de distribución con datos cualitativos, ya sea una distribución unimodal, bimodal, multimodal, uniforme o de variable aleatoria constante, cuando este no es el caso de las dos razones de variación previas de Freeman (1965) y Wilcox (1973). Además, el nuevo índice pretende incorporar más información sobre los datos nominales. Aparte de la frecuencia modal (f Mo ) en que se basa el índice de Freeman (1965), el número de categorías cualitativas (k) que añade el índice de Wilcox (1973), se planea agregar el número de modas o valores con frecuencia máxima (c).
Para el segundo objetivo de describir el patrón de comportamiento de los seis índices y colegir si el nuevo índice propuesto es adecuado, se generan nueve tablas de frecuencias; una tabla con dos categorías nominales y ocho tablas con cinco categorías nominales, las cuales corresponden a distintos tipos de distribución. La tabla de dos categorías corresponde a una distribución aleatoria discreta constante. Las otras tablas tienen una distribución próxima a la de una variable aleatoria discreta constante, próxima a la simetría en torno a una moda única, con simetría estricta en torno a una moda única, próxima a una distribución uniforme con una moda única, distribución uniforme, bimodal, trimodal y cuatrimodal.
Análisis de datos
Sobre las tablas de datos generados, se aplican las fórmulas de los seis índices de variación y se sintetizan los datos sobre los índices en una tabla resumen. Finalmente, se calculan las diferencias de RVU con los demás índices, y estas diferencias se resumen por medio del valor mínimo (Min), valor máximo (Max) y promedio o media aritmética de la diferencia en valor absoluto (M). Aparte, se computa la correlación producto-momento de Pearson (r) entre RVU y los demás índices. Para calcular esta medida de asociación, solo se requieren datos emparejados de dos variables cuantitativas continuas que son supuestos que se cumplen. Adicionalmente, se estiman estas correlaciones por intervalo con un nivel de confianza al 95% por el método de muestreo repetitivo de percentil corregido de sesgo y acelerado (IC CSA al 95%) con la simulación de 1000 muestras con el programa estadístico SPSS versión 26. Se consideró como la mejor opción por los tamaños muestrales muy pequeños, de 5 a 9 (Bishara & Hittner, 2017).
Resultados
Formulación del nuevo índice, la razón de variación universal (RVU)
La razón de variación se aplica solo cuando la distribución es unimodal o en el caso de que no tenga moda (distribución uniforme), argumentando que la frecuencia modal es nula. Si la muestra o la población tiene dos o más modas, esta medida de variación no se puede calcular. No obstante, la fórmula de Freeman (1965) se podría modificar para aplicarse con más de una moda y considerar el número de categorías. Para tal fin, propongo una expresión algebraica que se podría denominar razón de variación universal (RVU), debido a que se puede aplicar con cualquier tipo de distribución de variable cualitativa.
Partiendo de la fórmula de Freeman (1965), 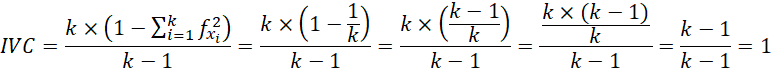 , la fórmula propuesta pondera la frecuencia relativa modal por el inverso del número de modas ( 1/c) y divide la expresión por su valor máximo. Este máximo se alcanza con la distribución uniforme, cuando c = k,
, la fórmula propuesta pondera la frecuencia relativa modal por el inverso del número de modas ( 1/c) y divide la expresión por su valor máximo. Este máximo se alcanza con la distribución uniforme, cuando c = k,  y
y  .
.
El mínimo, el máximo y los valores de RVU
Cuando un valor acapara toda la frecuencia (variable aleatoria constante), siendo la frecuencia modal única y con un valor unitario (c = 1 y f Max = 1), la razón de variación universal (RVU) alcanza su valor mínimo de 0.
Si no hay moda (distribución uniforme), todas las categorías tienen la misma frecuencia y dicha frecuencia es la máxima (1/k), el valor de c es k y la razón de variación universal (RVU) alcanza su valor máximo de 1.
En la medida que c se aproxima a k, siendo k el número de categorías (distribución uniforme), el resultado de la modificación propuesta se aproxima a 1:
Esto se debe a que, en la medida en que la muestra de la variable cualitativa X presenta más categorías con frecuencia máxima (c), el efecto sustractor de la frecuencia máxima disminuye en la razón de variación modificada (1- f Max /c) y, consecuentemente, el valor de esta medida de variación aumenta (RVU). Cuanto menor es el número de categorías (k), mayor es el incremento en la razón de variación universal (RVU), ya que se reparte más la variabilidad, alejándose la distribución de X de la de una variable constante (valor mínimo) y aproximándose más a la de una distribución uniforme (valor máximo).
Sea la frecuencia máxima (f
Max
) de .40 en todos los siguientes ejemplos. Si hay cuatro categorías cualitativas y una moda, el valor de RVU es .64; en caso de dos modas, se incrementa en .21 y pasa a ser .85
y pasa a ser .85 . Si hay seis categorías cualitativas y una moda, el valor de RVU es .62; en caso de dos modas, se incrementa en .206 y pasa a ser .823. Si hay 10 categorías cualitativas y hay una moda, el valor de RVU es .
. Si hay seis categorías cualitativas y una moda, el valor de RVU es .62; en caso de dos modas, se incrementa en .206 y pasa a ser .823. Si hay 10 categorías cualitativas y hay una moda, el valor de RVU es . ; en caso de dos modas se incrementa en .
; en caso de dos modas se incrementa en .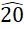 y pasa ser .
y pasa ser . (Tablas 1 y 2).
(Tablas 1 y 2).
Tabla 1 Incremento de la razón de variación universal (RVU) en función del valor de la frecuencia modal y número de modas en la muestra de una variable cualitativa con 4 o 6 categorías.

Nota. c = número de categorías con frecuencia relativa simple máxima, f Max = frecuencia relativa simple máxima, k = número de categorías o valores de la variable X, RVU = razón de variación universal y Δ = incremento o diferencia con el valor previo.
Tabla 2 Incremento de la razón de variación universal (RVU) en función del valor de la frecuencia modal y el número de modas en la muestra de una variable cualitativa con 10 categorías

Nota. c = número de categorías con frecuencia relativa simple máxima, f Max = frecuencia relativa simple máxima, k = número de categorías o valores de la variable X, RVU = razón de variación universal y Δ = incremento o diferencia con el valor previo.
Relación de RVU con RV y RVMod
En el caso de una moda (c = 1), que es la situación en que la fórmula de Freeman (1965) y la propuesta son comparables, la RVU arroja a un valormayor o igual que la de Freeman (1965), al igual que la razón de variación de la moda (RVMo) de Wilcox (1973).
Cuando el número de categorías cualitativas (k) es muy pequeño, hay mayor diferencia entre RVU y RV. Con dos categorías, la diferencia o incremento es de un tercio: RVU - RV = 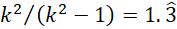 . Con tres categorías, la diferencia o incremento es de un octavo (RVU - RV = K
2
/(K
2
- 1) = 1.125). No obstante, en la medida que se incrementa el número de categorías, la diferencia es menor. Con cuatro categorías, la diferencia o incremento es de 1.0
. Con tres categorías, la diferencia o incremento es de un octavo (RVU - RV = K
2
/(K
2
- 1) = 1.125). No obstante, en la medida que se incrementa el número de categorías, la diferencia es menor. Con cuatro categorías, la diferencia o incremento es de 1.0 y, con cinco, de 1.041
y, con cinco, de 1.041 . Cuando el número de categorías tiende a infinito, RVU converge a RV.
. Cuando el número de categorías tiende a infinito, RVU converge a RV.
Retomando el ejemplo previo, sea la frecuencia modal única de .40, la razón de variación universal es de .64 con cuatro categorías cualitativas frente a la razón de variación de Freeman de .60. Si el número de categorías cualitativas es 6, la razón de variación universal es de .62 frente a .60 de la de Freeman. Si el número de categorías cualitativas es 10, la razón de variación universal es de . frente a .60 de la de Freeman.
frente a .60 de la de Freeman.
Al contrario que con RV, cuando hay una única categoría cualitativa con frecuencia máxima (c = 1), la nueva medida de variación propuesta, la razón de variación universal (RVU), es menor o igual que la razón de variación de la moda (RVMod) de Wilcox (1973). Consecuentemente, RV siempre toma un valor menor o igual que RVU, y RVU siempre toma un valor menor o igual que RVMod. Por ejemplo, si el número de categorías cualitativas es cinco (k = 5), la razón de variación (RV) de Freeman (1965) es 0.96 veces la razón de variación universal (RVU) y es 0.80 veces la razón de variación de la moda (RVMod) de Wilcox (1973).
Patrón de comportamiento de las seis medidas de variación
Distribución de una variable aleatoria discreta constante
Cuando la distribución de la variable nominal es la de una variable constante, una de las categorías cualitativas concentra toda la probabilidad. En esta situación, se pueden calcular los seis índices y todos ellos dan un valor de 0 (Tabla 3).
Tabla 3 Distribución de frecuencia de una muestra de una variable aleatoria discreta constante
| X | n i | fi | fi 2 | fi x ln(fi) | ( f Mo - fi)2 | fi(f Mo - fi)2 |
| a | 85 | 1 | 1 | 0 | 0 | 0 |
| No a | 0 | 0 | 0 | - | 1 | 0 |
| Σ | 85 | 1 | 1 | 0 | 1 | 0 |
Nota. n i = frecuencia absoluta simple, f i = frecuencia relativa simple, f Mo = frecuencia relativa simple de la categoría modal, Σ = suma por columna.
Número de categorías: k = 2.
Número de categorías con frecuencia máxima: c = 1. Número de modas = 1.
Frecuencia relativa máxima: f Max = 1. Frecuencia de la moda: f Mo = 1.
Razón de variación universal:
Razón de variación de la moda: 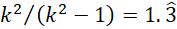 = (5/4) x 0 = 0
= (5/4) x 0 = 0
Índice de variación cualitativa: 
 = (2 x (1 − 1))/1 = 0/1 = 0
= (2 x (1 − 1))/1 = 0/1 = 0
Desviación estándar desde la moda:
Distribución próxima a la de una variable aleatoria discreta constante
Cuando la distribución de la variable nominal se aproxima a la distribución de una variable aleatoria constante, una de las categorías cualitativas concentra casi toda la probabilidad o frecuencia relativa simple. En esta situación, se pueden calcular los seis índices. Los índices RV, RVU, RVMod y SEM dan los valores más bajos, y IVC y ERel, los más altos, pero todos ellos valores próximos a 0 (Tablas 4 y 5).
Tabla 4 Distribución de frecuencias próxima a la de una variable constante

Nota. n i = frecuencia absoluta simple, f i = frecuencia relativa simple, f Mo = frecuencia relativa simple de la categoría modal, Σ = suma por columna. Tipo de distribución: PC = próxima a la de una variable aleatoria discreta constante, PS = próxima a la simetría en torno a la moda, S = distribución estrictamente simétrica en torno a la moda única, PU = distribución unimodal próxima a la distribución uniforme, U = distribución uniforme, BM = bimodal, TM = trimodal, CM = cuatrimodal
Distribución próxima a la simetría en torno a una moda única
La distribución de una variable nominal se aproxima a una distribución simétrica, si al ubicar a la categoría modal en el centro del diagrama de barras, el perfil se asemeja a un triángulo simétrico. Primero, se emparejan las categorías por probabilidad. Luego, se ponen al lado derecho y al lado izquierdo cada miembro del par, ordenando los pares por su valor de probabilidad en sentido ascendente a la izquierda de la moda y en sentido descendente a la derecha de la moda. En este caso, se pueden calcular los seis índices, al ser la distribución unimodal. Los índices IVC y ERel dan los valores más altos. Por el contrario, los índices RV y RVU dan los valores más bajos, así resultan más sensibles a una moda bien definida o destacada (Tablas 4 y 5).
Distribución con simetría estricta en torno a una moda única
La distribución de una variable nominal es simétrica, si al ubicar a la categoría modal en el centro del diagrama de barras, el perfil corresponde a un triángulo simétrico. Como en el párrafo previo se explicó, en primer lugar, se emparejan las categorías por probabilidad. A continuación, se pone al lado derecho y al lado izquierdo cada miembro del par, ordenando los pares por su valor de probabilidad en sentido ascendente a la izquierda de la moda y en sentido descendente a la derecha de la moda. En este caso, se pueden calcular los seis índices, ya que la distribución es unimodal. Los índices IVC y ERel dan los valores más altos. Por el contrario, los índices RV y RVU dan los valores más bajos, ya que resultan más sensible a una moda bien definida o destacada (Tablas 4 y 5).
Distribución próxima a una distribución uniforme con una moda única
Cuando la distribución de la variable nominal se aproxima a una distribución uniforme, sus distintas categorías tienen una probabilidad muy semejante. Si una frecuencia es ligeramente más alta que las demás, se pueden calcular los seis índices al ser la distribución unimodal. En este caso, los índices que más se aproximan a 1 son IVC y ERel. Los más bajos son la RV de Freeman y la modificación propuesta RVU (Tablas 4 y 5).
Distribución uniforme
Cuando la distribución de la variable nominal corresponde a una distribución uniforme, todas sus categorías cualitativas tienen la misma probabilidad o frecuencia relativa. En esta situación, se pueden calcular cinco de los seis índices. La razón de variación con respecto a la moda (RVMod) de Wilcox (1973) no se puede calcular porque queda fuera de rango [0, 1]. Los índices RV, RVU, DEM, IVC y ERel toman un valor de 1 (Tablas 4 y 5).
Distribución bimodal, trimodal y cuatrimodal
En el caso de una distribución bimodal o multimodal, no se puede calcular la razón de variación (RV) de Freeman (1965), ni la razón de variación de la moda (RVMod) de Wilcox (1973), aunque sí con la modificación propuesta (RVU). Los otros tres estadísticos (DEM, ICV y ERel) sí se pueden computar. La existencia de dos o más modas incrementa la variabilidad. El índice de variación cualitativa (ICV) de Gibbs y Poston (1975) es el que más se dispara al haber dos o más modas. La modificación propuesta o razón de variación universal (RVU) muestra un incremento más moderado con dos modas, y la desviación estándar desde la moda (DEM), con tres y cuatro modas (Tablas 4 y 5).
Tabla 5 Valores de los seis índices de variación en relación con nueve tipos de distribuciones
| c | Tipo de distribución | f Max | RV | RVU | RVMod | DEM | IVC | ERel |
| 1 | Constante | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | Próxima a una constante | .924 | .076 | .079 | .095 | .095 | .181 | .228 |
| 1 | Próxima a una simétrica | .433 | .567 | .590 | .708 | .700 | .890 | .871 |
| 1 | Simétrica | .5 | .5 | .521 | .625 | .618 | .831 | .801 |
| 1 | Próxima a una uniforme | .270 | .730 | .731 | .913 | .889 | .969 | .953 |
| 5 | Uniforme | 0 | 1 | 1 | 1 | 1 | 1 | |
| 2 | Bimodal | .256 | .908 | .917 | .985 | .982 | ||
| 3 | Trimodal | .240 | .959 | .930 | .985 | .981 | ||
| 4 | Cuatrimodal | .220 | .984 | .951 | .990 | .986 |
Nota. c = número de categorías con frecuencia máxima, f Max = frecuencia relativa simple máxima, RV = razón de variación de Freeman (1965), RVU = razón de variación universal, RVMod = razón de variación de la moda de Wilcox (1973), DEM = desviación estándar desde la moda de Kvalseth (1988), IVC = índice de variación cualitativa de Gibbs y Poston (1975) y ERel = entropía relativa de Shannon (1948).
La Tabla 6 permite apreciar que RVU es más afín al índice de Freeman (1965) que al de Wilcox (1973), así la diferencia promedio en valor absoluto de RVU es de .01 con RV versus .08 con RVMod. La correlación de RVU es unitaria con ambos índices (.9996, IC CSA al 95% [.9990, 1], con RV versus .9995, IC CSA al 95% [.9985, 1], con RVMod). En relación con los otros tres índices, la mayor afinidad se da con la desviación estándar desde la moda (DEM). La correlación entre RVU y DEM es .9842, IC CSA al 95% [0.9319, 0.9992], y la diferencia promedio en valor absoluto es de .05. La diferencia máxima entre RVU y DEM en valor absoluto es de .16 que se da en la distribución unimodal próxima a la uniforme. En esta diferencia, DEM tiene un valor más alto que RVU. Además, las correlaciones de RVU con IVC y ERel son significativamente menores que con RV y RVMod con un nivel de significación al 5%, ya que los límites superiores de los intervalos de confianza al 95% de las dos primeras correlaciones quedan por debajo de los límites inferiores de las dos últimas.
Tabla 6 Diferencia y correlación de RVU con los otros cinco índices de variación
| Estadísticos | RVU y RV | RVU y RVMod | RVU y DEM | RVU y IVC | RVU y ERel |
|---|---|---|---|---|---|
| Min(D) | 0 (C y U) | -.182 (PU) | -.158 (PU) | -.310 (S) | -.281 (PS) |
| Max(D) | .023 (PS) | 0 (C y U) | .033 (CM) | 0 (C y U) | 0 (C y U) |
| M(|D|) | .008 | .084 | .050 | .118 | .114 |
| r | 0.9996 | 0.9995 | 0.9842 | 0.9428 | 0.9492 |
| LI | 0.9990 | 0.9985 | 0.9319 | 0.8761 | 0.8956 |
| LS | 1 | 1 | 0.9992 | 0.9969 | 0.9980 |
Nota. Estadísticos: D = RVU - otro índice, |D| = |RVU - otro índice|, Min = valor mínimo, Max = valor máximo, M = promedio o media aritmética y r = coeficiente de correlación producto-momento de Pearson entre RVU y cada uno de los otros cinco índices; se estima un intervalo de confianza al 95% por el método de muestreo repetitivo de percentil corregido de sesgo y acelerado (IC CSA al 95%) con la simulación de 1000 muestras: LI = límite inferior y LS = límite superior. Índices de variación: RV = razón de variación de Freeman (1965), RVU = razón de variación universal, RVMod = razón de variación de la moda de Wilcox (1973), DEM = desviación estándar desde la moda de Kvalseth (1988), IVC = índice de variación cualitativa de Gibbs y Poston (1975) y ERel = entropía relativa de Shannon (1948). Tipo de distribución: C = de una variable aleatoria constante, U = uniforme, PU = unimodal próxima a una distribución uniforme, S = estrictamente simétrica, PS = próxima a una distribución simétrica.
Discusión
Desde los ejemplos presentados en el presente trabajo, se puede observar que la razón de variación (RV) de Freeman (1965)), la modificación propuesta o razón de variación universal (RVU), la razón de variación de la moda (RVMod) de Wilcox (1973) y la desviación estándar desde la moda (DEM) de Kvalseth (1988) son más sensibles, se aproximan más rápidamente a 0 que el índice de variación cualitativa (IVC) de Gibbs y Poston (1975) y la entropía relativa (ERel) de Shannon (1948) ante una distribución unimodal en la que la categoría modal concentra casi toda la probabilidad. En el caso de la distribución de una variable aleatoria constante, en la que una única categoría concentra toda la frecuencia, los seis índices son nulos. Por el contrario, ICV, ERel, RVMod y DEM frente a RV y RVU son más sensibles, se aproximan más rápidamente a 1, ante una distribución próxima a una uniforme, aunque con una moda poco definida, esto es, una distribución unimodal con frecuencias muy semejantes. Cuando la distribución es uniforme, lo que implica que todas las categorías tienen exactamente la misma probabilidad o frecuencia, el valor de los seis índices es 1, salvo la razón de variación de la moda (RVMod) de Wilcox (1973) que no se puede calcular. Cabe señalar que la razón de variación universal (RVU) se asemeja mucho a la razón de variación de Freeman cuando la distribución es unimodal. Cuanto más definida está la moda, la distribución se asemeja más a la de una variable constante para estos dos índices.
En caso de más de una moda, la razón de variación (RV) de Freeman (1965) y la razón de variación de la moda (RVMod) de Wilcox (1973) no se pueden calcular. Ante más de una moda, el incremento en el valor del índice se experimenta más fuerte en ICV y ERel. La razón de variación universal (RVU) es la más moderada en su incremento con dos modas y la desviación estándar desde la moda (DEM) con más de dos modas. Cabe señalar que el comportamiento entre la nueva razón de variación y la desviación estándar desde la moda es muy afín. Comparten el 96.9% de la varianza ante los distintos tipos de distribución para datos nominales, con una diferencia máxima de .05. Esta se da con la distribución unimodal próxima a la uniforme. DEM ante esta distribución. Ante una bimodal, la diferencia entre ambos índices es mínima a favor de DEM y con más modas sigue siendo una diferencia muy pequeña, pero a favor de RVU. Ante una distribución estrictamente uniforme los dos índices son unitarios.
Considerando el comportamiento y posibilidades de cálculo de las seis medidas de variación cualitativa revisadas, se concluye que la desviación desde la moda (DEM) de Kvalseth (1988), en primer lugar, y la propuesta de la razón de variación universal (RVU), en segundo lugar, son las medidas más recomendables para medir la variación con variables cualitativas, ya que son las menos extremas en su comportamiento. DEM tiene la ventaja que, con muestras grandes, permite el uso de estadística inferencial paramétrica y, claramente, RVU es la mejor entre las tres razones de variación. Además, RVU y DEM son muy afines, esto es, sus valores discrepan poco, cuando este es un problema al usar diversas medidas de variación de datos nominales (Agresti & Agresti, 1978). Con fundamento en su rango de 0 a 1 y el planteamiento de RVU como una proporción, se podrían usar los puntos de corte de un escalamiento min-max. Valores menores que .20 o .30 se pueden considerar indicadores de baja variabilidad, entre .30 y .70 o .20 y .80 media y mayores que .70 o .80 alta (Sree & Bindu, 2018).
Como limitaciones del estudio se tiene el uso de un único ejemplo por distribución en vez de usar metodología de simulación con la generación de miles de muestras aleatorias, por ejemplo, o tabla-población (Morris, White, & Crowther, 2019). Aunque se intentó cubrir todas las posibles distribuciones cualitativas, solo se incluyeron cinco categorías cualitativas, salvo dos con la distribución de una variable aleatoria constante. Así, el número de categorías cualitativas podría ser una variable a considerar en futuros estudios sobre el comportamiento de los índices de variación cualitativa (Evren & Erhan, 2017).
Se recomienda usar y estudiar con más profundidad los índices de variación cualitativa, ya que es una información muy relevante a nivel descriptivo. La desviación estándar desde la moda, más compleja de cálculo, y la razón de variación universal, más sencilla de cómputo, son dos buenas opciones sin que existe una marcada discrepancia entre las mismas, por el contrario, son muy afines. Se sugiere ampliar este estudio aplicando métodos de simulación con distribuciones de variables cualitativas manipulando el número de categorías nominales.