Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Entramado
Print version ISSN 1900-3803
Entramado vol.12 no.2 Cali July/Dec. 2016
https://doi.org/10.18041/entramado.2016v12n2.24219
http://dx.doi.org/10.18041/entramado.2016v12n2.24219
Una dimensión didáctica y conceptual de un instrumento para la Valoración de Objetos Virtuales de Aprendizaje. El caso de las fracciones
A methodological and conceptual dimension of a tool for the evaluation of Virtual Learning Objects. The case of fractions
Uma dimensão didática e conceptual de um instrumento para a avaliação de Objetos Virtuais de Aprendizagem. O caso das fracções
Mónica María Triana-Muñoz*, Juan Fernando Ceballos-Londoño**, Jhony Alexander Villa-Ochoa***
* Magíster en Educación Matemática de la Universidad de Medellín. Docente de Matemáticas en la I.E. Escuela Normal Superior María Auxiliadora, del municipio de Copacabana, Antioquia - Colombia. monikelatri@yahoo.es.
** Magíster en Educación Matemática de la Universidad de Medellín. Docente de Matemáticas en la I.E. Santo Tomás de Aquino del municipio de Guarne, Antioquia - Colombia. juanferceballos@hotmail.com.
*** Doctor en Educación de la Universidad de Antioquia. Docente de la Universidad de Antioquia. Coordinador de la Red Colombiana de Modelación en Educación Matemática (RECOMEM). Coordinador Grupo MATHEMA-Formación en Investigación en Educación Matemática Universidad de Antioquia, Antioquia - Colombia. jhony.villa@udea.edu.co.
Este es un artículo Open Access bajo la licencia BY-NC-SA (http://creativecommons.org/licenses/by-nc-sa/4.0/)
Cómo citar este artículo: TRIANA-MUÑOZ, Mónica María; CEBALLOS-LONDOÑO, Juan Fernando; VILLA-OCHOA, Jhony Alexander. Una dimensión didáctica y conceptual de un instrumento para la Valoración de Objetos Virtuales de Aprendizaje. El caso de las fracciones. En: Entramado. Julio - Diciembre, 2016 vol. 12, no. 2, p. 166-186, http://dx.doi.org/10.18041/entramado.2016v12n2.24219.
Recibido: 08/02/2016 Aceptado: 05/05/2016
Resumen
Estudios realizados sobre el tema de valoración de objetos virtuales de aprendizaje han aportado instrumentos que en gran medida han sido pensados para atender la generalidad de aspectos estructurales y no han profundizado en aspectos metodológicos, ni han atendido a particularidades intrínsecas de los conocimientos propios de una disciplina, lo que sugirió la necesidad de proponer e investigar sobre la definición de las características de un instrumento de valoración, atendiendo a las particularidades de las matemáticas y de sus contenidos. Para consolidar la construcción del instrumento de valoración de objetos virtuales de aprendizaje, se llegó a la conclusión que este debería atender a la relación entre el contenido, la pedagogía y la tecnología, aspectos que se profundizan en el marco teórico de la investigación. Un instrumento de carácter didáctico-conceptual, que abarca varias dimensiones y cuenta con unas orientaciones generales para los temas del área de matemáticas, en específico para la enseñanza de las fracciones, proporcionando un espacio de participación al profesor para la construcción del instrumento como tal. El instrumento de valoración fue validado en varias etapas, donde fueron partícipes profesores de matemáticas de diferentes niveles educativos. Como resultado de este proceso investigativo surgió un Instrumento nombrado "Valoración de Objetos Virtuales de Aprendizaje para la enseñanza de las fracciones", que pretendió llenar el vacío estructural y de contenido identificado en los demás instrumentos existentes.
Palabras clave: OVA, TIC, profesor enseñanza, instrumento y criterios de valoración.
Abstract
Studies about the subject of valuation of virtual learning objects have contributed with instruments which are largely designed to serve the generality of structural aspects and they have not gone deeply in methodological aspects or they have attended intrinsic peculiarities of discipline-specific knowledge, which suggested the need to propose and investigate on the definition of the characteristics of a measurement instrument attending to the particularities of mathematics and their contents. To strengthen the construction of the instrument for the evaluation of virtual learning objects it was reached the conclusion that this should address the relationship between the content, pedagogy and technology, aspects that deepens in the theoretical framework of research. An instrument of didactic-conceptual character which encompasses several dimensions, and has general guidelines for subjects in the area of mathematics, in particular for the teaching of fractions, providing a space for participation to the Teacher for the construction of the instrument as such. The assessment instrument was validated in several stages, where they were involved math teachers from different educational levels. As a result of this research process emerged an instrument named "Valuation ofVirtual Learning Objects for Teaching Fractions", which sought to fill the empty structural and content identified in other existing instruments.
Keywords: OVA, ICT, teacher education, instrument and valuation criteria.
Resumo
Estudos sobre o tema da avaliação de objetos virtuais de aprendizagem, têm fornecido ferramentas que foram em grande parte destinados a abordar a generalidade dos aspectos estruturais, e não já mergulhou em aspectos metodológicos, nem tenham frequentado peculiaridades intrínsecas da experiência de uma disciplina; Ele está sugerindo a necessidade de propor e investigar sobre a definição das características de um instrumento de avaliação, com base nas especificidades de matemática e seu conteúdo. Para fortalecer a construção dos objetos virtuais de aprendizagem instrumento de avaliação, concluiu-se que esta deve abordar a relação entre aspectos de conteúdo, pedagogia e tecnologia que aprofundam no referencial teórico da investigação. Um instrumento de natureza didático-conceitual, abrangendo várias dimensões e tem diretrizes gerais para os problemas na área da matemática, especificamente para fracções de ensino, proporcionando um espaço de participação para o professor para a construção do instrumento como tal. A ferramenta de avaliação foi validada em várias etapas, onde os professores de matemática eram participantes de diferentes níveis de ensino. Como resultado deste processo de investigação um instrumento designado "ranking Objetos Virtuais de Aprendizagem para frações de ensino", que visam preencher a estrutura vazia e conteúdos identificados nos outros instrumentos existentes surgiram.
Palavras-chave: OVA, TIC, professor, instrução, instrumento e critérios de valoração.
Introducción
La integración de las "Tecnologías de la información y la comunicación (TIC) en el aula ha ocupado un lugar importante en las agendas de diversos investigadores, algunos de ellos se han preocupado por los usos que se tienen de las tecnologías en Educación Matemática (Borba, Scucuglia & Gadanidis, 2014), otros por comprender los fenómenos involucrados en los usos que hacen los profesores (Vi-lla-Ochoa, Galvis, Sierra & Vélez, 2014); otros se han preocupado por establecer constructos teóricos que permitan generar comprensiones sobre las relaciones entre profesores, estudiantes, tecnologías y contextos escolares, entre otros (Borba & Villarreal, 2005).
A pesar que las TIC se presentan como aspecto central en la producción de conocimiento matemático, existen diferentes factores por los cuales algunos profesores no las integran en el aula. En un reciente estudio en Brasil, Oliveira (2014) encontró que aspectos como la infraestructura y la falta de preparación eran los más recurrentes en los argumentos con los cuales los profesores justificaban el no uso de tecnologías. En Colombia, el estudio de Villa-Ochoa et al. (2014) señaló que, aunque los profesores socialmente reconocen la importancia de la tecnología, al interior del aula de clase no la usan, en parte, por la mirada que tienen de estos recursos como complementos (opcionales) y no porque reconocen su rol en la producción de conocimiento matemático.
El uso de la tecnología en el aula de matemáticas debe valorarse por la naturaleza del conocimiento que se puede construir y no solo porque podría ofrecer motivación o facilitar el aprendizaje. En esta visión de tecnología para la producción de conocimiento, el docente se consolida como un agente fundamental e irremplazable, es decir, las TIC nunca podrán desplazar a dicho actor (Borba y Villarreal, 2005). Para Borba y Villarreal (2005) tanto los humanos como las tecnologías (no humanas) juegan un papel constitutivo en la producción de conocimiento matemático y no se subordinan ni se yuxtaponen entre sí; la presencia del profesor y su conocimiento da sentido a otras tecnologías como la oralidad, sin la cual los procesos educativos cambiarían su naturaleza. En coherencia con los planteamientos de estos investigadores, Villa-Ochoa,Vélez, Rojas y Borba (2013) realizaron un estudio en el que reportaron la necesidad que los profesores de matemática "vivan experiencias con tecnologías y matemáticas" a partir de las cuales se reflexione sobre los roles y usos de las tecnologías, en particular, experimenten su rol en la reorganización de los modos de producción de conocimiento matemático; para los autores, estas experiencias en las que se involucran los profesores cumplen un papel importante a la hora de integrar las TIC en las matemáticas escolares.
Castillo (2008) refiere que los docentes que integran las TIC deben determinar y clasificar el tipo de situaciones que propicien el aprendizaje y la comprensión del conocimiento matemático; la valoración precisa de un análisis situacional que inicia con una búsqueda de aquellas situaciones donde tiene sentido el uso del conocimiento matemático considerado y se lleva a cabo una labor de categorización, selección, organización y simplificación. Se hace necesario posibilitarle al profesor herramientas que medien en la integración de TIC a sus procesos de enseñanza, para que tenga criterios definidos al momento de usar dichas herramientas y se trascienda del instrumentalismo, es decir, de un uso netamente procedimental de las TIC a un uso que propicie el aprendizaje. Con base en ello, una adecuada integración de las TIC debe plantearse más allá del uso del recurso material, es decir, debe atender a los aspectos propios del aprendizaje de las disciplinas y principios que generen procesos educativos, en el caso específico de este artículo, los contenidos, principios y procesos están asociados a la matemática.
De acuerdo con los planteamientos anteriores, se observa la necesidad rastrear en la literatura aquellas investigaciones que aporten criterios para que los profesores reconozcan y valoren los usos, posibilidades y limitaciones en los procesos de enseñanza y de aprendizaje de los objetos matemáticos.
El uso pedagógico de las TIC, en particular la valoración e implementación de objetos virtuales de aprendizaje (OVA), juega un papel clave en las matemáticas escolares, puesto que apoya la organización de contenidos digitales en unidades de aprendizaje que pueden ser utilizadas en diferentes contextos; asimismo, permite la construcción de conocimientos y el desarrollo de habilidades cognitivas al igual que la posibilidad de realizar diferentes representaciones de los objetos matemáticos; al respecto, Wong (2012) puntualiza que cuando se utiliza un computador o material de aprendizaje digital en una situación de aprendizaje se espera que se haga para introducir un valor añadido a este proceso diferente al que se lograría con el material impreso.
Se han propuesto diversos instrumentos de valoración para la selección de herramientas tecnológicas, a nivel general se ha creado el Modelo de Calidad establecido por el estándar ISO 9126 para la evaluación de la calidad de productos de software.
[...] el cual fue publicado en 1992, con el nombre de "Information technology -Software product evaluation: Quality characteristics and guidelines for their use", en el cual se establecen las características de calidad para productos de software. El estándar ISO-9126 establece que cualquier componente de la calidad del software puede ser descrito en términos de una o más de seis características básicas, las cuales son: funcionalidad, confiabilidad, usabili-dad, eficiencia, mantenibilidad y portatilidad; cada una de ellas se detalla a través de un conjunto de subcaracterísticas que permiten profundizar en la evaluación de la calidad de productos de software. (Figueroa, 2005, p.l)
A nivel más específico, en la literatura internacional fue posible encontrar propuestas de diferentes autores con respecto a la evaluación de calidad de OVA, relacionadas en la Tabla 1.
En las investigaciones descritas en la Tabla 1 es posible reconocer un interés por la evaluación de calidad para los OVA. Este interés se ubica en general en percepciones estructurales de la herramienta en sí misma y de su contenido a nivel interno; sin embargo, no referencian la mirada del profesor y las necesidades que la herramienta permitiría cubrir a nivel de procesos de enseñanza en un área específica; lo anterior llevó a pensar en la necesidad de describir y formular las características de un instrumento de valoración de OVA, lo que implica un mirada que integre enfoques técnico, pedagógico, conceptual y didáctico para un área y contenido específico (matemáticas-números fraccionarios). Un instrumento que articule estas componentes debería posibilitar a los profesores mayores y mejores criterios para la selección de un OVA que satisfaga sus propósitos formativos en el aula.
La existencia de recursos de baja calidad y la carencia de evaluaciones profundas y sistemáticas puede provocar en los profesores usuarios desinterés o desconfianza a la hora de reutilizar un OVA. La razón principal para preocuparse por la calidad es que se trata de recursos de apoyo al aprendizaje. Aun cuando no es el único factor que afecta los procesos de enseñanza y aprendizaje, la carencia de controles de calidad puede afectar el proceso y sus resultados en los aprendices. La mayoría de las propuestas de modelos de evaluación de la calidad consideran solo algunas características de los mismos, lo que no permite lograr una evaluación integral (Vidal, 2008).
Tener criterios para valorar el potencial que un recurso digital (OVA) ofrece al profesor le brinda la posibilidad de acercarse crítica y reflexivamente a la comprensión de la complejidad, potencial y limitaciones de tal recurso; aportaría también visiones para enfrentar retos del momento actual de la educación, la cual se presume inmersa en el fenómeno de la integración de las TIC. En este sentido trabajar con OVA se ha convertido en una oportunidad más para identificar el potencial de las TIC como mediadores del aprendizaje. Es preciso reconocerlos como un concepto vivo, es decir, que es posible, si no deseable, que este concepto cambie con el tiempo, madure, evolucione, se asiente dentro de la cultura y las prácticas tanto de los docentes como de los estudiantes (Chiappe, 2009).
Los elementos anteriores permitieron delimitar el campo de trabajo dentro de los OVA y el uso que los profesores les dan a ellos, lo que ayudó a identificar la necesidad de valorar dichas herramientas antes de ser usadas. En este sentido, este artículo se propone ofreecer una respuesta a la pregunta ¿Cuáles son las características que se deben tener presentes en un instrumento que permita a los profesores discriminar y valorar OVA para la enseñanza de un contenido matemático? El artículo se desprende de una investigación más amplia, denominada "Valoración de Objetos Virtuales de Aprendizaje para la enseñanza de las matemáticas. Instrumento para profesores", la cual se desarrolló en el marco de la maestría en Educacion matemática de la Universidad de Medellín; en su repositorio se encuentra un informe con otros resultados del estudio.
1. Antecedentes Teóricos
1.1. Integración y uso de TIC en el aula
El entorno de enseñanza donde actúa el profesor ha de ser un espacio de continuo cambio, sin dejar de ser él quien de forma directa aporta a la formación matemática de los estudiantes, es él quien está llamado a implementar recursos para lograr tal propósito. Según planteamientos de Andrade (2012), es necesario rediseñar los modelos académicos, siguiendo las tendencias educativas internacionales, cambiar y repensar las prácticas, para integrar las TIC en la enseñanza diaria y para promover la creación de comunidades académicas que operan a través de las redes de interacción y desarrollar materiales didácticos que promuevan el aprendizaje. Además, es conveniente posibilitarle al profesor herramientas que medien en este proceso de integración de TIC a sus procesos de enseñanza en el aula, para que tenga criterios definidos al momento de usar dichas herramientas y se trascienda del instrumentalismo a un uso pedagógico de ellas.
La integración y uso de las TIC en las matemáticas escolares requiere que los profesores desarrollen visiones articuladas de la Tecnología. En coherencia con ello, Hadjerrouit (2010) considera la tecnología, el contenido y la pedagogía no de forma aislada, sino más bien relacionando tres componentes claves, a saber:
- El conocimiento de la pedagogía que se aplica a los contenidos específicos.
- El conocimiento de cómo la tecnología puede apoyar los objetivos pedagógicos.
- El conocimiento de cómo la asignatura se transforma por la aplicación de la tecnología. Claramente, el conocimiento técnico de los profesores por sí solo no es suficiente para alcanzar los resultados de aprendizaje.
Un reto para el profesor que integra TIC es el uso de los recursos tecnológicos con criterios pedagógicos claros, por lo anterior y para responder a ese reto, el uso e integración de TIC al aula implica por parte de él una reflexión profunda sobre la usabilidad de la herramienta a integrar; al respecto, Hadjerrouit (2010) ha señalado que el reto de la utilización de TIC es que el profesor trascienda del instrumentalismo tecnológico y, sobre ello, puntualiza que
[...] el valor añadido de los recursos de aprendizaje basados en la web (WBLRs) en términos de aprendizaje vendrá de una mejor comprensión de las cuestiones pedagógicas y no de forma automática a partir de una mejor tecnología. Es evidente que el diseño y evaluación de WBLRs deben ir más alla de la facilidad de uso técnico e incluir aspectos que son pertinentes para el aprendizaje y la pedagogía (Hadjerrouit, 20l0, p.2).
Entre los recursos y herramientas a las que pueden acceder los profesores se encuentran los OVA; a continuación se presenta una caracterización de los mismos.
1.2. Los OVA; su uso e integración en los procesos de enseñanza
El software educativo incluye una amplia variedad de posibilidades; en la descripción presentada en el apartado anterior puede inferirse, en términos generales, que el profesor puede usar tales herramientas teniendo como eje primordial aquellas prácticas que tocan con el proceso de enseñanza. En este sentido, se profundiza en el estudio de un medio didáctico más concreto, el cual es denominado "Objeto Virtual de Aprendizaje" (OVA), que a su vez tiene la misma finalidad del software educativo, retomado como un recurso que presta apoyo tanto al docente como al estudiante, promueve y estimula el aprendizaje autónomo, el trabajo colaborativo entre docentes y alumnos. Cubides (2013) afirma: "Un objeto de aprendizaje es cualquier entidad, digital o no digital, la cual puede ser usada, reusada o referenciada durante el aprendizaje, educación o entretenimiento apoyado por tecnología" (p.6).
Los OVA ofrecen recursos y estrategias metodológicos que al ser usados en el aula los estudiantes pueden contemplar los aspectos conceptuales y didácticos que permitan mejorar el aprendizaje, además, posibilitan que el acercamiento a los diferentes objetos matemáticos se dé significativamente. Sus características a nivel general son:
(...) las características de los OVA han sido descritas por Agudelo (2008) y el Ministerio de Educación Nacional de Colombia, en Cubides (20l3) se proponen las siguientes características a las que a nivel general deben responder los objetos de aprendizaje:
Reutilizable: Ser reutilizado es su principal característica, un objeto de aprendizaje cuenta con la capacidad de ser usado varias veces en contextos y propósitos educativos diversos, al ser identificados con los metadatos pueden ser localizados independientemente.
Interoperable: Tiene la capacidad de ser importado o exportado para integrarse en estructura y plataforma de difusión diferente. Evita costos económicos en el desarrollo de contenidos para una tecnología cuando se cambia de plataforma.
Accesible: Cuentan con la facilidad para ser identificados, buscados y encontrados gracias al correspondiente etiquetado a través de diversos descriptores (metadatos) que permiten la catalogación y almacenamiento en el correspondiente repositorio.
Durable: Deben ser diseñados de tal forma que la vigencia de la información de los objetos sea duradera, y que los cambios tecnológicos no lo alteren.
Autónomo: Los objetos deben ser autónomos, con respecto de los sistemas desde los que fueron creados.
Flexible: Su versatilidad y funcionalidad les dan elasticidad para combinarse en muy diversas propuestas y generar nuevos objetos de áreas diferentes del saber.
Estas características, miradas de forma integrada, aportan también insumos para que el profesor pueda valorar los OVA, asimismo, permiten centrar la atención en sus componentes y fundamentar su uso en las prácticas pedagógicas del profesor. Sin embargo, frente a las posibilidades que ofrece para el desarrollo conceptual y de capacidades en los estudiantes los aportes de estos criterios no son claros. Una vez más se argumenta la necesidad de que la valoración hecha por los profesores no se puede quedar sólo en la predicción, debe trascender a evaluar la calidad de la usabilidad pedagógica, es decir, el diálogo entre el profesor y el OVA a utilizar, la utilidad pedagógica del mismo como material pedagógico de aprendizaje y que presenta las posibilidades y debilidades al momento de ser implementada. Utilizar OVA como herramienta educativa ofrece para los profesores posibilidades de enseñanza, lo cual va ligado directamente a las intenciones de éste al integrar cierto objeto virtual, lo que es denominado "facilidad de uso pedagógico", dimensión que está asociada con aspectos que son fundamentales para el aprendizaje. Por lo tanto, para hacer frente a las cuestiones pedagógicas, "la usabilidad técnica debe extenderse a capturar elementos que son pertinentes para el aprendizaje" (Hadjerrouit, 2010).
1.3. La valoración de OVA
Conforme se mencionó en el primer apartado de este artículo, en la literatura internacional existen propuestas que pretenden aportar criterios para que los profesores valoren el uso de OVA al interior de sus aulas. En la perspectiva Villodre y Llanera (2011) se hace referencia a la pertinencia de analizar un OVA con una visión que integre elementos como: los contenidos (qué se aprende), los procesos (cómo se aprende) y las condiciones de aprendizaje (lo que ha de cumplir una actividad o una situación para que el aprendizaje se produzca). Para el caso de las matemáticas, la Educación Matemática, como disciplina científica, ha ofrecido insumos para atender a estos tres elementos.
En la perspectiva del diseño de recursos, Almera y Hueros (1999) proponen principios que hacen parte del diseño de un software educativo, entre ellos: la relación entre el conocimiento previo, utilidad del conocimiento, contexto donde se aprende, conocimiento contextualizado. Para los autores, dada la significación que estos materiales están adquiriendo en el terreno educativo, se hace más urgente su reflexión en cuanto a la estructura organizativa y didáctica que presenta, de manera que se proporcione al profesor herramientas que respondan a las necesidades no sólo sofisticadas desde el punto estético, técnico y rentable, sino facilitadoras para un aprendizaje más efectivo.
Algunos criterios para evaluar OVA reúnen cuatro enfoques que se consideran valiosos por sus aportes para que el profesor tenga la posibilidad de retomarlo para el desarrollo de sus clases, esos cuatro enfoques son: "aspectos psicopedagógicos: capacidad de motivación, adecuación a destinatarios, profundidad y relevancia disciplinar; aspectos didáctico-curriculares: relacionado con objetivos del currí-culo y contexto en que se aplicará; aspectos técnicos-estéticos: adecuación a estándares, legibilidad, colores, tamaño, resolución, diseño de interfaz y aspectos funcionales: facilidad de uso, accesibilidad, eficacia" (Morales, 2005, p. 4). A pesar de recomendarse la integracion de estos cuatro enfoques, en ocasiones se evidencia más énfasis en valorar aspectos psicopedagógicos, que los que tienen que ver con la didáctica y el currículo (Morales, 2005).
Con el ánino de atender a las diferentes esferas que implica la valoración de los recursos que se implementan en las clases, se presta también atención al componente de la formación y el conocimiento del profesor; en el siguiente apartado se desarrollaran los principales aspectos que se tuvieron en cuenta en la investigación que dio origen a este artículo.
1.4. Del conocimiento profesional para la enseñanza a la formación del profesor en y para el uso de TIC
Conocimiento pedagógico y tecnológico del contenido
Al interior de la Educación Matemática existen diversidad de enfoques y perspectivas en relacion con el conocimiento que un profesor debe desarrollar para ejercer su labor de manera competente. Entre los constructos que más han llamado la atención se encuentra el conocimiento pedagógico del contenido del profesor de matemáticas. Aunque la naturaleza de este conocimiento puede parecer obvia, se trata de darle una nueva mirada al proceso de enseñanza en la perspectiva de la formación docente, en donde no solamente se habla de la enseñanza de las matemáticas (un caso específico), sino también de las matemáticas utilizadas en la enseñanza y la naturaleza del conocimiento matemático para dicho proceso (Ball, Thames, y Phelps, 2008).
En la preocupación por conceptualizar sobre el conocimiento del profesor, Shulman (1986) y sus colegas, citados por Ball et al. (2008) desarrollaron tipologías para caracterizar el conocimiento profesional para la enseñanza así:
- Conocimiento pedagógico general, con especial referencia a aquellos principios amplios y estrategias de manejo de la clase y la organización que parecen trascender el tema.
- El conocimiento de los alumnos y sus características.
- El conocimiento de los contextos educativos, que van desde trabajos del grupo o aula, la gestión y la financiación de los proyectos escolares, al carácter de las comunidades y culturas.
- Conocimiento de los fines educativos, propósitos y valores, y sus fundamentos filosóficos e históricos.
- Conocimiento del contenido.
- Conocimiento del currículo, con especial comprensión de los materiales y programas que sirven como herramientas de trabajo para los profesores.
- Conocimiento pedagógico del contenido, que amalgama contenido y pedagogía.
Las tres últimas categorías definen las dimensiones del contenido específico y, en conjunto, constituyen a lo que se refiere Shulman (1986) como el paradigma que falta en la investigación sobre la enseñanza, un "punto ciego" con respecto al contenido que caracteriza a la mayoría de investigaciones sobre la enseñanza.
En esta misma línea de argumentación se hace referencia a que históricamente la formación de profesores ha estado centrada en el contenido y ha definido el conocimiento pedagógico del contenido como la forma más útil de representación de las ideas. Las más potentes analogías, ilustraciones, ejemplos, explicaciones y demostraciones, son la forma más útil de representar y formular el tema; esto hace que sea comprensible para los demás. El conocimiento pedagógico del contenido también incluye una comprensión que hace que el aprendizaje de temas específicos sea más fácil o más difícil.
Grossman (1990) citado por Ball et al. (2008) señaló que tales ideas son inherentes a los planteamientos de Dewey con respecto a que los profesores deben aprender a "psi-cologizar" su materia de enseñanza, repensar temas disciplinarios para hacerlos más accesibles a los estudiantes. Los profesores deben aprovechar su conocimiento de la materia para seleccionar temas apropiados y su conocimiento de los saberes previos de los alumnos y sus concepciones para formular representaciones apropiadas y provocativas de los contenidos que se deben aprender.
Frente al conocimiento del profesor de matemáticas Ball et al. (2008) centraron su atención, en primera instancia, en la manera como los profesores necesitan aprender el contenido pedagógico y, segundo, en determinar qué necesitan saber sobre las matemáticas y cómo y dónde pueden ellos utilizar este conocimiento matemático en la práctica. El resultado de tal investigación fue que el análisis de errores es una práctica común entre los matemáticos en el curso de su propio trabajo; la tarea de la enseñanza sólo difiere en que se centra en los errores producidos por los estudiantes, pero el profesor más que lo anterior debe averiguar lo que los ellos han hecho, si el pensamiento es matemáticamente correcto para el problema, y si el enfoque funcionaría en general, debe conocer razones para realizar procedimientos, significados para términos y explicaciones de conceptos, deben hacer y entender el fin de enseñar las matemáticas. Un profesor tendrá que conocer los contenidos que enseña, en el caso de este estudio, deberá saber cuáles procesos y procedimientos promueven los recursos (OVA), cuándo promueven concepciones erróneas, procedimientos imprecisos; así mismo, deberá reconocer las posibilidades de actuación que desempeñarán sus estudiantes cuando se enfrenten a esos recursos y valorarlos después de su desempeños ante ellos.
Frente al conocimiento del profesor en relación con la tecnología, se han desarrollado marcos para interpretar y comprender lo que el profesor debería conocer y saber hacer en cuanto a los recursos de que dispone. Jang y Chen (2010) afirman que para que la tecnología se convierta en una herramienta integral para el aprendizaje, los profesores deben desarrollar una concepción global de su objeto de estudio con respecto a ella y del significado de enseñar con tecnología. En este caso, el conocimiento sobre el contenido (C), la pedagogía (P), y la tecnología (T) es fundamental para el desarrollo de una buena enseñanza. Sin embargo, en vez de realizar un tratamiento aislado de cada uno de estos aspectos como independientes, se levanta la mirada y se en-fatiza particularmente en cómo lograr su interacción; es así como el TPCK (Mishra y Koehler, 2006) se propone como un contructo teórico para la integración del desarrollo del conocimiento de la materia, con la tecnología y la enseñanza de los contenidos.
Koehler (2007 citado por Syh-Jong et al., 20Í0) declaró que el TPCK es una forma situada de conocimientos necesarios para el uso inteligente de la tecnología en la enseñanza y el aprendizaje. En el corazón de TPCK está la dinámica transaccional; relación entre el contenido, la pedagogía y la tecnología. La buena enseñanza con tecnología requiere la comprensión de las relaciones que se refuerzan mutuamente entre los tres elementos tomados juntos para desarrollar estrategias y representaciones específicas del contexto apropiado. En este sentido, si el profesor tiene buenos conocimientos en informática, ello no sería condición suficiente para que con la implementación de esta tecnología, pretenda enseñar un contenido matemático, ya que también es necesario tener una apropiación de los contenidos a enseñar y de las estrategias didácticas a utilizar. De la misma manera, si el profesor tiene un conocimiento sobre cierta temática, no necesariamente conjuga las maneras y la pertinencia de los recursos para enseñarlo, por eso es preciso disponer de herramientas para ello.
Por su parte, Angeli y Valanides (2009) proponen cinco criterios para evaluar el TPCK en la enseñanza con tecnología. Primero la identificación de los temas a ser enseñados con la tecnología, en formas que representen un valor añadido, es decir, tener en cuenta, por ejemplo, los temas que los estudiantes no pueden comprender fácilmente, o temas en que los profesores enfrentan dificultades en la enseñanza. A continuación, la identificación de las representaciones en la transformación del contenido a ser enseñado, de manera que estos sean comprensibles para los estudiantes. Posteriormente la identificación de las estrategias de enseñanza, que son difíciles o imposibles de ser implementadas con los medios tradicionales. Tener en cuenta también la selección de equipos y herramientas apropiados, además de usos pedagógicos eficaces; y por último la identificación de estrategias adecuadas para combinarse con la tecnología en el aula y poner al estudiante en el centro del proceso de aprendizaje.
Hasta este punto se muestra la existencia del TPCK y la relación que debe existir entre sus componentes, de manera tal que no basta con una buena formación tecnológica por parte del profesor, tampoco es suficiente una formación matemática para garantizar buenos resultados de los procesos de enseñanza dentro del aula, más bien, se deja entrever que es fundamental la integración de estos componentes a través de estrategias pedagógicas. Pero ¿cómo lograr contribuir a dicha integración? Se presenta entonces el establecimiento de las características de un instrumento de valoración de OVA como una oportunidad de aproximarse a una respuesta a este interrogante.
En contraste con el punto de vista de la tecnología, tratada simplemente como una artefacto de apoyo, la postura en la que se quiso aportar fue en enfatizar las conexiones e interacciones entre los contenidos, la pedagogía y la tecnología, la cual se logra cuando un profesor sabe con cuáles herramientas tecnológicas puede transformar estrategias pedagógicas y las representaciones de contenido de temas específicos, pero: ¿Qué necesitan los profesores para adquirir una comprensión de las complejas relaciones entre contenidos, pedagogía y tecnología? Una postura externa al TPCK sugeriría que los profesores necesitan ser preparados en el uso de la tecnología, pero desde un punto de vista más integral se puede decir que una de las formas de alcanzar un buen nivel potencial en el uso de la tecnología en el aula y en el caso más específico de la integración de OVA en los procesos de enseñanza de las matemáticas, tiene que ver con la participación del profesor en un proceso de valoración, apropiación y crítica de los recursos a usar, con criterios pensados a partir de él y que le den argumentos para usar creativamente estas tecnologías a fin de satisfacer objetivos pedagógicos específicos de determinadas áreas, en este caso concreto, el área de matemática.
2. Metodología
En esta investigación se asume que la integración de la tecnología en las aulas de clase no se agota en proporcionar los artefactos o materiales, ya que esta se presenta no solo como un mediador para alcanzar un fin sino como una herramienta fundamental en la producción de conocimiento; desde esta perspectiva un profesor debe estar en capacidad de pensar, reelaborar y analizar críticamente los materiales a utilizar, entender la integración de la tecnología como un proceso dinámico; el profesor es un constructor, un académico que piensa y que propone, y no un mero ejecutor de un instrumento entregado, es decir, el profesor no es un técnico de la educación.
La visión de conocimiento que como equipo de investigación se asumió, pone en dialéctica dos aspectos fundamentales del conocimiento: las propuestas teóricas y las empíricas. En este sentido se parte de una necesidad empírica, fundamentada en la necesidad que tienen algunos profesores, acerca de la existencia de criterios de valoración de OVA y de un instrumento con características particulares pesadas para él, necesarios para la selección e integración de estos en los procesos de enseñanza del área de matemáticas y en temas específicos de la misma, lo cual se fundamentó en la revisión de la literatura.
En concordancia con lo anterior, el estudio que se reporta en este artículo fue de carácter cualitativo en el sentido que se describieron, comprendieron e interpretaron los fenómenos a través de las percepciones y significados producidos por las experiencias de los participantes. Se realizaron interpretaciones no solo de los diálogos, sino también, de sus palabras y sus acciones, lo que posibilitó construir miradas más amplias, que permitieron entender los aspectos comunes a muchas personas y grupos humanos en el proceso de producción y apropiación de la realidad social y cultural en la que desarrollan su existencia (Sandoval, 1996).
El camino seguido en todo momento de la investigación, desde la génesis de las ideas a investigar hasta la obtención de datos, su análisis y conclusiones; se describen a continuación.
Del conocimiento profesional para la enseñanza, a la formación del profesor en el uso de TIC, acá se enfatizó la necesidad de la relación entre el conocimiento de tres componentes de los principales ambientes de aprendizaje los cuales son el contenido, la pedagogía y la tecnología.
En el proceso, luego de consolidar el marco teórico, se inició la consolidación del instrumento de valoración de OVA. Se comenzó con la elaboración de instrumentos a nivel general (listas de chequeo, rúbricas, tablas, cuadros, etc.); sin embargo, después de analizar y debatir (de marzo de 2014 a julio de 2015) como equipo de investigación se llegó a la conclusión de que el instrumento debería atender a los aspectos que habían sido descuidados en otras investigaciones; puntualmente, la relación entre el contenido, la pedagogía y la tecnología y, para ello se pensó en un instrumento que además de criterios técnicos, estéticos, funcionales, incluyera un componente didáctico-conceptual, es decir, que incluya un conjunto de criterios para reconocer las potencialides de la OVA para promover diversidad de significados, usos, procedimintos y otros aspectos conceptuales propios de la temática (este artículo se fundamenta en la temática de las fracciones).
2.2. Fase de diseño y validación del instrumento
2.2.1. Fase de diseño
En la literatura se encontraron instrumentos de valoración de OVA que en sus diseños presentaban criterios para valorar su calidad en aspectos como la presentación estética de los contenidos (Ver Tabla 1). A nivel general, muchos de ellos se constituian en listas de chequeo que asignaban puntuaciones numéricas de acuerdo con los estándares de calidad que eran nombrados, además se evidenció una falta de participación de los profesores en el proceso de valoración de tales recursos. En la revisión no se encontraron instrumentos que permitieran realizar valoraciones para temas específicos del área de matemáticas.
Fundamentación de la estructura del instrumento
De acuerdo con lo anterior, se pensó en la construcción de un instrumento que estuviera diseñado para profesores; que les permitiera valorar las dimensiones estética y técnica, pero que además, les facilitara profundizar en el conocimiento del contenido que enseña integrado a la tecnología que usa (dimensión Didáctico-Conceptual). La dimensión didáctico-conceptual del instrumento se propone para atender a la preocupación tanto por el contenido específico como por la estrategia utilizada para la enseñanza; bajo esta perspectiva, más allá de ser un formulario que se diligencia, es un instrumento para la reflexión y análisis de los aspectos conceptuales y sus procesos de enseñanza. El instrumento, más allá de buscar juicios de valor, pretende constituirse en un insumo para explicitar las ventajas y limitaciones de la utilización de las TIC para la enseñanza de determinado contenido matemático.
Teniendo en cuenta el direccionamiento formativo del instrumento, la preocupación por la reflexión de los profesores sobre sus propios procesos de enseñanza estuvo siempre presente. Para ello, la herramienta debería posibilitar al profesor una identificación de sí mismo en su labor, su formación, los procedimientos usados y sus necesidades; su relación con el uso de la tecnología; en la conjunción de estos aspectos se pretende aproximarse a una interacción en el contenido, lo pedagógico, lo didáctico y lo tecnológico.
2.2.2. Fase de validación del instrumento
Validación interna
Luego de diseñado el instrumento, el equipo de investigadores se dio a la tarea de ponerlo a prueba a través de la valoración de diferentes OVA gratuitos de la web; a partir de allí, se hicieron ajustes de forma y de contenido y se adecuaron categorías para su análisis. Entre los ajustes que se hicieron se tiene; agrupación de criterios que hacían referencia al mismo aspecto a valorar o ya estaban contenidos en otras dimensiones; la ausencia de criterios que permitieran una participación activa del profesor; y la coherencia con los referentes teóricos usados.
Validación externa: un pilotaje con potenciales usuarios
Después del proceso interno de validación dentro del equipo de investigación, se hizo un pilotaje con profesores en formación y en ejercicio del área de matemáticas. Se pidió a los participantes que una vez diligenciaran el instrumento manifestaran sus sensaciones, dificultades, fortalezas, tanto desde el punto de vista técnico como de su estructura didáctica y conceptual; a partir de este pilotaje hubo otros ajustes en la redacción y el contenido. Posterior a este proceso de validación se generó el instrumento "Valoración de Objetos Virtuales de Aprendizaje (OVA) para la enseñanza de las Fracciones" el cual se detalla en su estructura más adelante, en la presentación de los resultados.
Toma de datos y validación empírica
Para esta fase se diseñó y desarrolló un estudio con cinco profesores de matemáticas que enseñaban en los diferentes niveles educativos: (1) Básica Primaria, (1) Básica Secundaria, (2) Media y (1) Universitario, todos ellos de instituciones educativas públicas. Éstos fueron nombrados en nuestro proyecto de investigación con los seudónimos de Erick, Sergio, Yulian, Luisa y Andrés.
La formación profesional con que contaban los profesores era diversa; el grupo de participantes estuvo conformado por profesionales no formados como profesores (no licenciados), profesionales formados como profesores de matemáticas (licenciados) y algunos de ellos con títulos de maestría en TIC o en enseñanza de las ciencias exactas y naturales. La decisión de trabajar con este grupo de profesores fue tomada porque al interior de sus prácticas tenían el propósito de utilizar las TIC como apoyo a los procesos formativos en matemáticas; asimismo, por su preocupación por cambiar y re-pensar constantemente sus prácticas de enseñanza.
En consecuencia con lo planteado en el marco teórico y con el propósito de trascender el instrumentalismo tecnológico, el estudio se constituyó en una indagación empírica que permitió recolectar y valorar información a partir del diligenciamiento del instrumento propuesto y posteriormente, a través de una entrevista no estructurada. En la Tabla 2 se muestra la estructura de cada una de las fases, las actividades y sus respectivos propósitos.
El diseño de la investigación fue ideado de manera que se permitiera encontrar puntos de convergencia o divergencia entre la información suministrada en cada actividad de recolección de datos. El análisis de estos datos permitió hacer las comparaciones de las consideraciones de los profesores en el proceso de validación del instrumento, los cuales se presentan a continuación.
El instrumento utilizado en este proceso de investigación "Valoración de Objetos Virtuales de Aprendizaje (OVA) para la enseñanza de las fracciones", se elaboró a través de un formulario de Google Drive, el cual se puede encontrar en el siguiente link https://docs.google.com/forms/d/1ByCHym013VxFdQMvA-uhB8d0A2k76sICJRRPtPpbKTY/viewform?c=0&w=1&usp=mail_form_link, y se estructuró en dos partes:
La primera estuvo direccionada por los objetivos de la investigación lo cual requirió una caracterización de cada uno de los profesores en cuanto nombre, grado de escolaridad, niveles de ejercicio docente, áreas de formación académica, concepciones sobre la integración de TIC en el aula de clase, su frecuencia de uso y criterios tenidos en cuenta para la selección OVA en Internet.
La segunda parte del instrumento fue encaminada hacia un componente más teórico, referido a ese saber específico que los profesores deberían tener al momento de la selección de los OVA; para este proceso investigativo fueron elegidas las fracciones como tema en particular. Los aspectos formativos de dicho tema en específico tenidos en cuenta en esta segunda parte del instrumento fueron: la fracción como relación parte-todo, la fracción como punto sobre la recta numérica, la fracción como cociente, la fracción como índice comparativo, los algoritmos de las operaciones entre fraccionarios y su utilización para la resolución de situaciones problemas, las representaciones semióticas de los fraccionarios y las relaciones entre ellas y, por último, una reflexión por parte de los profesores acerca de los procesos generales que tienen que ver con el aprendizaje en el área de matemáticas y que se pueden desarrollar con OVA, identificando a su vez aspectos limitantes para el proceso de enseñanza aprendizaje de las fracciones.
3. Resultados
En este artículo se presentan los resultados organizados en dos secciones, en la primera "presentación estructural del instrumento" se muestra el instrumento como tal, la cate-gorización de sus preguntas y su estructura general. Luego, en la segunda sección "Análisis de resultados de la validación empírica" se presenta cada una de las dimensiones que conforman el instrumento, al igual que las informaciones dadas por los profesores.
3.1. Presentación estructural del instrumento
En primera instancia, se encuentra el título "Valoración de Objetos Virtuales de Aprendizaje (OVA) para la enseñanza de las fracciones" y un párrafo introductorio, con lo cual se propone una orientación frente al contenido y objetivo del instumento. A continuación de transcribe el contenido en mención:
Seguidamente se presentó una parte del instrumento titulada "Caracterización del Docente" con el cual se pretendía obtener una caracterización de los participantes con datos como: nombre, último grado de escolaridad, niveles de ejercicio docente y áreas de formación. Luego se encuentran cuatro preguntas (de la número cinco a la número ocho), las cuales se proponen identificar aspectos como la postura que tienen los profesores sobre la integración de las TIC en el aula con su respectiva justificación, además la frecuencia con la que usan tecnologías en sus clases y los criterios que tienen en cuenta para la selección o no del material a usar.
En la pregunta ocho específicamente se buscó generar un espacio de reflexión por parte de los profesores de sus propia práctica pedagógica, en cuanto al reto presente que implica la implementación de las TIC y el uso de los recursos tecnológicos con criterios pedagógicos claros y cómo valoraba cada uno de ellos para implementarlos en el aula de clase.
5. De las siguientes posturas sobre la integración de las TIC en el aula de clase, indique con cuál se identifica y por qué:
- En ocasiones las TIC son una herramienta que permite una mayor interacción entre el estudiante, el maestro y el conocimiento matemático.
- La importancia de la tecnología, al interior del aula de clase es reconocida, sin embargo no se usa, en parte, por la mirada que se tiene de estos recursos como complementos (opcionales) y no como herramientas que constituyen la producción de conocimiento matemático.
- La incorporación de nuevos métodos de enseñanza, como la implementación de las TIC en el aula de clase, poco contribuye al desarrollo de competencias en el área de matemáticas.
- Las TIC son un apoyo para los procesos dina-mizados por el maestro, especialmente cuando los recursos que él usa le permiten al estudiante interactuar experimentar desde un modelo académico que implique cambiar y re-pensar constantemente la enseñanza y las prácticas que esta incluye.
- Por qué:______________________________________________________________________
6. ¿Implementa usted las TIC en el aula? ¿Con qué frecuencia lo hace?
Sí ______ No__________ Frecuencia:
*A diario
*Semanalmente
*Quincenalmente
*Mensualmente
*Eventualmente, solo cuando las necesito
7. Cuando usted va a realizar la enseñanza de un tema específico de la matemática y recurre al Internet en búsqueda de material didáctico, ¿cuáles son los criterios que tiene en cuenta para la selección o no de dicho material?
_____________________________________________________________________________________
8. Lea el siguiente párrafo: Un reto presente que implica la implementación de las TIC es que el profesor use los recursos tecnológicos con criterios pedagógicos claros, es decir, que en realidad comprenda que no solo por disponer de un computador y que los estudiantes lo manipulen se logra una integración óptima, además reflexione en qué momento herramientas como los OVA se convierten en mediadores de procesos que se usan para enriquecer la amplia gama de posibilidades y experiencias de enseñanza, que no son fáciles de vivenciar en al aula tradicional, como el acceso a información de calidad de forma ágil y el desarrollo de tareas interactivas.
Según la apreciación anterior, describa brevemente cómo valora usted sus acciones frente al uso de las TIC en el aula de clase.
_____________________________________________________________________________________
En el final de esta primera parte del instrumento, se presentó un mensaje de agradecimiento a los profesores por la información brindada al diligenciar el instrumento y por su aporte significativo al desarrollo de la investigación y se invitó a continuar respondiendo las preguntas de la siguiente sesión, de la manera más objetiva posible.
La segunda parte inicia con un fragmento del instrumento llamado "Primera valoración específica de un OVA". Este fragmento se acompaña de una imagen que ilustra la cantidad de información que existe en la web y la importancia de tener criterios de clasificación y selección. En esta parte, el instrumento sugirió al profesor la temática de las fracciones y, por tanto, debía seleccionar un OVA en la temática para hacer su análisis.
Primera valoración específica de un OVA
En la pregunta número nueve se solicitó al profesor que seleccionara, copiara y pegara la URL del OVA con el propósito de que posteriormente se pudiese ubicar y analizar el OVA trabajado.
9. Dirección web del OVA
Selecciona, copia y pega la URL del OVA:__________________________________________________
La siguiente pregunta se propuso con el fin de que el profesor identificara en el OVA y seleccionara cuál o cuáles de los procesos generales, de los declarados en los Estándares Básicos de Competencias colombianos, eran promovidos en su OVA elegido; posteriormente se le pedía que proporcionara un ejemplo. La pregunta y el ejemplo pedido tienen como propósito reconocer que el conocimiento del profesor para la enseñanza de las fracciones no se inscribe solo en las definiciones, proceso y algoritmo, sino también en los procesos, actuaciones, aplicaciones, usos y significados que las fracciones tienen en diferentes contextos y representaciones.
10. Según los Estándares Básicos para el Área de Matemáticas, todas las áreas curriculares pueden considerarse procesos semejantes y en cada una de esas áreas estos procesos tienen peculiaridades distintas y deben superar obstáculos diferentes que dependen de la naturaleza de los saberes propios de la respectiva disciplina. Según lo anterior cuál(es) de los procesos generales que tienen que ver con el aprendizaje en el área de matemáticas permite desarrollar el OVA. Presente un ejemplo:
- Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Ello requiere analizar la situación: identificar lo relevante en ella; establecer relaciones entre sus componentes y con situaciones semejantes: formarse modelos mentales de ella y representarlos externamente en distintos registros: formular distintos problemas, posibles preguntas y posibles respuestas que surjan a partir de ella. Este proceso general requiere del uso flexible de conceptos, procedimientos y diversos lenguajes para expresar las ideas matemáticas pertinentes y para formular, reformular tratar y resolver los problemas asociados a dicha situación. Estas actividades también integran el razonamiento, en tanto exigen formular argumentos que justifiquen los análisis y procedimientos realizados y la validez de las soluciones propuestas.
- Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y con ellas, formular y sustentar puntos de vista. Es decir, dominar con fluidez distintos recursos y registros del lenguaje cotidiano y de los distintos lenguajes matemáticos.
- Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración.
- Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y por qué usarlos de manera flexible y eficaz. Así se vincula la habilidad procedimental con la comprensión conceptual que fundamenta esos procedimientos.
Posteriormente se presentaron las preguntas de la decimoprimera a la decimocuarta, las cuales hacen referencia al conocimiento del contenido, que es el conocimiento sobre el tema de fondo que hay que aprender o enseñar, en este caso las fracciones. Estas preguntas ofrecen una descripción de lo que se quiere valorar.
11. La relación parte-todo se presenta cuando un "todo" (continuo o discreto) se divide en partes "congruentes" (equivalentes como cantidad de superficie o cantidad de objetos). La fracción indica la relación que existe entre un número de partes y el número total de partes. De los siguientes aspectos seleccione los que son considerados en el OVA
- Dada una unidad o un todo discreto, todas sus fracciones tienen sentido, es decir, no se presentan situaciones tales como "hallar los 2/7 de un grupo de 12 personas" en donde el resultado carece de sentido real.
- Contribuye a la comprensión por parte del estudiante con respecto a la unidad como un todo y al todo como unidad.
- Permite el entendimiento de la fracción como medida en diferentes situaciones en contextos discretos y continuos.
- Se tiene en cuenta el concepto de "congruencia" para poder justificar el por qué algunas regiones sombreadas no pueden ser expresadas como fracciones.
12. Las fracciones como puntos sobre la recta numérica se presentan en situaciones donde se asocia la fracción a/b con un punto situado sobre la recta numérica en la que cada segmento unidad se ha dividido en b partes (o en un múltiplo de b) congruentes de las que se toman "a" partes
Al analizar este aspecto en el OVA, seleccione cuál(es) considera se posibilitan al trabajar dicho objeto virtual:
- Permite comprender que la fracción no se asocia siempre a una parte de una figura o a un subconjunto de objetos
- Contribuye a la percepción de las fracciones como un ente abstracto, es decir, posibilita la percepción de las fracciones como números naturales o número entre dos de estos
- Hace que las fracciones impropias (fracciones mayores que la unidad) aparezcan de forma más natural, así como la notación como números mixtos
- Tienen conexiones con la idea de medida (uso de escalas)
13. Una fracción es interpretada como un cociente cuando se asocia la fracción a la operación de dividir un número natural por otro (división indicada a:b =a/b)
De los siguientes aspectos, cuál(es) se evidencian en el OVA:
- Facilidad en la relación que existe entre la fracción 3/5 y la división 3:5 (por ejemplo)
- Se convierte en trabajo previo a la resolución de ecuaciones, al plantearse situaciones como "repartir tres barras de chocolate entre cinco niños de forma equitativa, igual a 5.X=3"
- Importancia de la "construcción" de las operaciones con los propios niños
- Desarrollo de situaciones de comparación y ordenación en donde los niños construyen procedimientos de solución mediante el proceso de dividir, ordenar medir y componer...
- Utilización de modelos de apoyo (regiones o segmentos, recta numérica, tablas de razones... ) y situaciones problemáticas (situaciones de la vida diaria) que sirvan de conexión entre las situaciones problemáticas en diferentes contextos y el trabajo numérico
14. Algunas veces las fracciones son utilizadas como un "índice comparativo" entre dos cantidades de una magnitud (comparación de situaciones). Así nos encontramos con el uso de las fracciones como razones. En este caso no existe de forma natural una unidad (un "todo") como podría ocurrir en los otros casos. Cuál(es) de las siguientes posibilidades de trabajo permite el OVA:
*Probabilidad *Relación entre cantidades *Porcentajes *Proporcionalidad *Otro
Las anteriores preguntas se proponen orientar al profesor usuario frente a los aspectos básicos relacionados con el tema de las fracciones, los cuales fueron la relación parte todo, las fracciones como puntos sobre la recta numérica, la interpretación de las fracciones como un cociente y las fracciones usadas como índice comparativo entre dos cantidades de una magnitud. Lo anterior se consideró importante, ya que siendo consecuentes con Graham (2011) y Mishra y Koehler (2006) hasta hace poco, la mayoría de las tecnologías utilizadas en las aulas se ha convertido en algo habitual y no eran ni siquiera consideradas como tecnologías; por esta razón, la tecnología está implícita en las concepciones de los investigadores en el conocimiento pedagógico del contenido. En este sentido la tecnología podría ser considerada como una parte del conocimiento de los contenidos curriculares o incluso las representaciones y de los medios de comunicación. Shulman (1986) explicó que el concepto de conocimiento curricular fue incluido en el concepto conocimiento del contenido, donde el conocimiento curricu-lar se define como conocimiento de los profesores de los instrumentos y materiales educativos, incluyendo software, programas, materiales audiovisuales, y las películas.
Las preguntas de la decimoquinta a la decimoséptima hicieron parte del componente didáctico, en él se incluían el conocimiento de las técnicas, metodologías, estrategias y métodos que el profesor usa y puede usar con su estudiantes para construir conocimientos, desarrollar habilidades y actitudes positivas hacia el aprendizaje. Un espacio donde los profesores pudieran reflexionar a través de interrogantes sobre el uso y sentido de los algoritmos y la resolución de problemas y cómo estos podrían ayudarles a clarificar su postura personal con respecto a la relación de determinados aspectos de las fracciones; además cómo el uso de los esquemas pictóricos o registros iconográficos en el OVA pueden aportar a la comprensión de aspectos relacionados con los números en su representación fraccionaria, asimismo, permite indagar por las limitaciones que los porfesores observan en el OVA para el estudio de la temática.
15. Algunas de las objeciones que se realizan a la enseñanza de las operaciones con fracciones (a la enseñanza de los algoritmos), es que estos algoritmos se convierten en reglas sin sentido para los niños. Lógicamente, si el niño está manejando reglas sin ningún sentido para él, resulta bastante natural que a lo largo del tiempo, deje de utilizarlas y las sustituya por otros procedimientos más "naturales" o, que olviden o modifiquen algún procedimiento en el algoritmo, convirtiéndolo así en un procedimiento erróneo. Según este enunciado, ¿cuál(es) de los siguientes interrogantes sobre el manejo de los algoritmos y la resolución de problemas, podrían ayudarnos a clarificar nuestra postura personal con respecto a la relación de determinados aspectos de las fracciones en la escuela al trabajar con el OVA?
- ¿Son los algoritmos de las operaciones con fracciones los procesos naturales para resolver el tipo de problemas que se plantean a los niños?
- ¿Conectamos el proceso de resolución de problemas con la utilización del algoritmo?
- ¿Podemos utilizar los procesos de resolución de problemas como caminos para la conceptualiza-ción de la operación (en este caso el algoritmo) y no sólo como aplicación?
- ¿Realmente son necesarios los algoritmos de las operaciones con fracciones para resolver esos problemas?
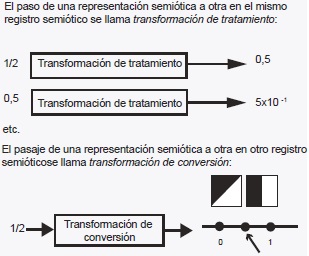
16. En la imagen anterior se ilustran algunas representaciones semióticas de los fraccionarios y las relaciones entre ellas. Según esta, ¿cómo considera usted que el uso de los esquemas pictóricos o registros iconográficos en el OVA aporta a la comprensión de conceptos relacionados con los números fraccionarios?
_____________________________________
17. Después de terminar el análisis del OVA, describa cuáles son esos aspectos (si existen) que se presentan como limitantes para el proceso de enseñanza-aprendizaje de los números fraccionarios:
_____________________________________
Seguidamente, se presentan otras dos secciones donde se le pide al profesor realizar el análisis de otros dos OVA diferentes al primero, para lo cual se usa nuevamente el instrumento en las preguntas comprendidas entre la novena y la decimoséptima. Con ello se espera que el profesor pueda disponer de variedad de OVA y pueda usar los criterios para fundamentar su elección y uso en el aula de clase.
3.2. Resultados de la validación empírica
Este apartado se fundamenta en los casos de Erick, Sergio, Yulian, Luisa y Andrés, los cinco profesores de matemáticas que participaron del diligenciamiento del instrumento. Los datos se analizaron y los resultados se organizaron en cuatro categorías, a saber: la formativa, la conceptual, la didáctica y la referida al uso y aplicaciones de los OVA. Como equipo de investigación se realizó un análisis de cada una de las respuestas dadas por ellos, con el propósito de encontrar puntos de convergencia y/o divergencia de tales consideraciones y ubicarlas en cada una de las categorías según las valoraciones hechas a los OVA a través del instrumento.
3.2.1. Categoría Formativa
Esta categoría hace alusión a los aspectos relacionados con las consideraciones que tienen los profesores frente a la integración de las TIC y a los retos en el uso de OVA para la enseñanza de las matemáticas. La Tabla 3 presenta evidencias frente a esta categoría.
Aunque el objetivo principal de este proyecto de investigación no fue el analizar las consideraciones de los profesores sobre el uso de TIC en el aula, resulta importante anotar que el instrumento permitió identificar puntos de convergencia que pudieron ser expresados en la siguiente idea: "Las TIC como apoyo al docente, contribuyen al mejoramiento de la calidad educativa y a potencializar el aprendizaje de las matemáticas en los estudiantes, logrando con la implementación de estas nuevas prácticas de aula, mayores niveles de interés y motivación". Los profesores manifestaron que el trabajo con OVA como un recurso mediador permite el trabajo colaborativo y el aprendizaje de forma dinámica, ya que algunos de estos permiten la visualización de aspectos que con tiza y tablero serían difíciles de percibir y trabajar. Para los profesores, es importante tener en cuenta que dicho trabajo de integración debe ser precedido por una selección asertiva del material a utilizar. En relación con el TPCK, la interacción entre la tecnología y el contenido puede dinamizar la conceptualización y la práctica, lo que a su vez contribuye a los procesos de enseñanza.
3.2.2. Categoría Conceptual
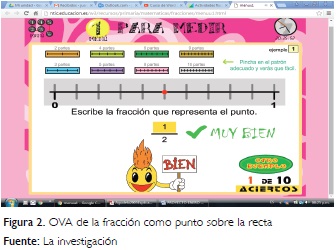
Esta categoría hace alusión a los aspectos relacionados con los conceptos específicos del área de matemáticas trabajados en los OVA. Conforme se ha mencionado anteriormente, el Instrumentoque se diseñó en esta investigación debía ofrecer orientaciones al profesor (usuario) con respecto a los aspectos conceptuales que intervinieran en los OVA analizados por ellos; para el caso del tema de las fracciones el Instrumento que se diseñó tenía como propósito centrar la atención y valorar el aporte de los OVA en: unidad como un todo y al todo como una unidad (pregunta II). Al respecto, los profesores manifestaron que el Instrumento les permitió identificar que los OVA valorados en su gran mayoría contribuían a la comprensión por parte del estudiante en relación con este concepto, ya que como lo manifestó la profesora Luisa en la exploración de uno de los OVA que seleccionó (http://juegosmatematicos.jimdo.com/fracciones/actividades-flash/) este permitía dicho trabajo puesto que retoma uno de los aspectos de la relación parte-todo (Ver Figura 1). En ella, la fracción indica la relación que existe entre un número de partes y el número total de partes, además en un nivel básico, también permitían el entendimiento de la fracción como medida en diferentes situaciones en contextos discretos. Una revisión al OVA analizado permite identificar que la fracción indica la existencia de un número de partes y el número total de partes; sin embargo no se hace énfasis en la relación entre estas dos cantidades. Aunque la profesora hizo uso de su conocimiento específico con respecto al tema (conocimiento del contenido); dicho conocimiento no corresponde a lo que la investigación denomina como "fracción como relación parte-todo". En ese sentido, ni el aporte de información presentado en el instrumento ni el conocimiento del contenido que poseía la profesora fueron suficientes para identificar las limitaciones del OVA y realizar críticas a este recurso. Por tanto, se requiere de otras experiencias que le permitan dinamizar su conocimiento del contenido en relación con el conocimiento de la tecnología; pues el hecho que un recurso ofrezca imágenes de partes de una figura, no es suficiente para promover la comprensión de la fracción; es decir, no solo con cortar y manipular partes de una figura se logra establecer la relación parte-todo como un significado de la fracción. En ese sentido, el uso del OVA no logra trascender la interpretación de la fracción como la "acción de partir" y parece reafirmar las prácticas clásicas que se hacen sobre las fracciones en las aulas escolares.
Con respecto al trabajo con la fracción como punto sobre la recta numérica (pregunta 12 en cada OVA) los profesores reconocieron en varios de los OVA una contribución en diferentes niveles de los aspectos propuestos para la valoración (A manera de ejemplo, se puede visitar: http://ntic.educacion.es/w3/recursos/primaria/matematicas/fracciones/menuu1.html). Entre los aspectos que los profesores resaltaron están: (i) permite comprender que la fracción no se asocia siempre a una parte de una figura o a un sub-conjunto de objetos, (ii) es un medio para enseñar la ubicación de fracciones en una recta numérica (Ver Figura 2). Al indagar por las razones de estos argumentos, apelaron a que el OVA permite coordinar la representación gráfica de la fraccion, gráfica de la recta real y numérica; además "le indica al estudiante si su respuesta es correcta o no, por lo cual el estudiante puede pasar a seguir intentándolo" Si bien es cierto que la OVA posibilita la coordinación entre varios sistemas de representación, lo más importante es el uso que hace de una representación gráfica (rectángulos de colores en la parte superior) como medio para coordinar los significados en la recta numerica y la representación aritmética. A pesar de ello, una vez más se cuestiona la ausencia de una interpretación de las fracciones como relación parte-todo y, en cuanto a los procesos, la posibilidad de discusión sobre la validez de los razomanientos queda oculto en una etiqueta de correcta o no. Una vez más, el conocimiento de las fracciones que tiene el profesor no fue suficiente para cuestionar las limitaciones del recurso frente a los procesos de validación que pueden desarrollarse a lo largo de estas prácticas.
Por su parte, el Instrumento de valoración permitió identificar a los profesores, que en diez de los doce OVA valorados por ellos, la interpretación de la fracción como un cociente (pregunta 13) posibilita el desarrollo de situaciones de comparación y ordenación en las que los estudiantes pueden construir procedimientos de solución mediante procesos de dividir, ordenar, medir, componer, etc. (Ver Figura 3). Al respecto el profesor Sergio, después de analizar un OVA (http://www.educaplus.org/cat-5-p1-Fracciones_Matem%25-C3%A1ticas.html) señaló que "permite el trabajo en lo que respecta a las fracciones equivalentes" Lo anterior fue valorado por el profesor, pues hace parte de los aspectos conceptuales y procedimentales que él reconoce están presentes en todo proceso de enseñanza de las fracciones; una vez más, el OVA legitima ciertas prácticas que se hacen con lápiz y papel, solo que en este caso mejora su presentación visual y manipulación.
A través del instrumento, Andrés reconoció en los OVA la exploración de la representación en porcentajes, relación entre cantidades y proporcionalidad (Ver ilustración 4), permiten la comprensión de las fracciones utilizadas como un "índice comparativo" entre dos cantidades de una magnitud (comparación de situaciones).
3.2.3. Categoría didáctica
Esta categoría hace alusión a los aspectos relacionados con los criterios de selección de OVA y las estrategias empleados por los profesores en los procesos de enseñanza y de aprendizaje de las matemáticas (preguntas 7, 15, 16, 17).
La Tabla 4 muestra una síntesis de los principales criterios de selección que tienen en cuenta los profesores participantes de este estudio al momento de seleccionar OVA disponibles en Internet. A partir de los datos consignados en la Tabla, se observa que los profesores convergen en sus consideraciones frente a aspectos didácticos como la posibilidad que tenía el estudiante de interactuar con el material. Este tipo de consideraciones pueden inscribirse en el denominado conocimiento pedagógico del contenido. Llama la atención que no hubo mención al uso de la herramienta como exploración conceptual, establecimiento de patrones y conjeturas. Los principales argumentos estuvieron más en acciones para concentrar la atención del estudiante lo cual es una evidencia de la existencia de una visión de las OVA como 'una opción más para el aprendizaje' y no como una herramienta constitutiva del conocimiento (Villa-Ochoa et al., 2013); la presencia de este tipo de visiones representa un llamado hacia la necesidad de tener más y mejores relaciones entre el conocimiento pedagógico del contenido y el conocimiento tecnológico; en la conjunción de estos dos conocimientos se configura el conocimiento pedagógico y tecnológico del contenido el cual representa una clase de conocimiento fundamental para el trabajo de los docentes con la tecnología (Mishra, 2006). Este modelo de integración de la tecnología en enseñanza y aprendizaje sostiene que el desarrollo de un buen contenido requiere un entrelazamiento reflexivo de las tres principales fuentes de conocimiento: la tecnología, la pedagogía y el contenido. En ese sentido, una mirada que subordine el rol de la tecnologia a un aditamento pero no reorganice los ambientes de aprendizaje, poco facilita la constitución de ese entrelazamiento. Promover el desarrollo de un conocimiento que entrelace el contenido, la pedagogía y la tecnología implica reconocer que no existe una transferencia automática entre uno y otro; y que por el contrario, se deben promover experiencias que permitan interacciones entre esos contenidos. En ese sentido, la dimensión didáctico-conceptual del instrumento utilizado en este estudio ofrece insumos para cuestionar un uso no reflexivo ni crítico de los OVA.
Conforme se mencionó anteriormente, la dimensión didác-tico-conceptual del instrumento se propuso promover reflexiones en torno a la propia práctica del profesor. Algunas de las preguntas en el instrumento generaron la posibilidad de que el profesor se cuestionara frente a sus procesos de enseñanza de los algoritmos y resolución de problemas en mayor medida. A través de preguntas como ¿Se pueden utilizar los procesos de resolución de problemas como caminos para la conceptualización de la operación (en este caso el algoritmo) y no sólo como aplicación? y ¿Se conecta el proceso de resolución de problemas a la utilización del algoritmo? Los profesores reconocieron que no era suficiente 'retratar' un contenido en el OVA sino que más allá de ello, se deben implicar otros aspectos de tipo pedagógico (la partipación e interacción con los estudiantes, el acceso y la manipulación del OVA, entre otros) u otros de tipo didáctico (los usos, significados, aplicaciones y los procesos que debería estar inmersos). En la entrevista realizada a los participantes, Erick anotó que "estas preguntas: la 15, 24 y 33, me parecieron muy importantes ya que me hicieron reflexionar acerca de lo importante que es que los algoritmos tengan sentido para los niños, y no queden solamente en procedimientos mecánicos y sin sentido que no permitan la comprensión y correcto uso para la resolución de problemas".
Como aporte a la comprensión que permite el OVA por parte de los estudiantes en cuanto a los conceptos relacionados con los números fraccionarios (pregunta 16), los profesores manifestaron en la entrevista su percepción frente a lo valioso y formativo del instrumento, en cuanto a la información brindada sobre el paso de una representación semiótica a otra, en el mismo o en diferente registro semiótico. A partir de ello, manifestaron la importancia de la utilización de esquemas pictóricos o registros iconográficos en el OVA como aporte a la comprensión de conceptos relacionados con las fracciones. La Tabla 5 recoge algunos aspectos mencionados por los profesores en el diligenciamiento del instrumento y/o en la entrevista.
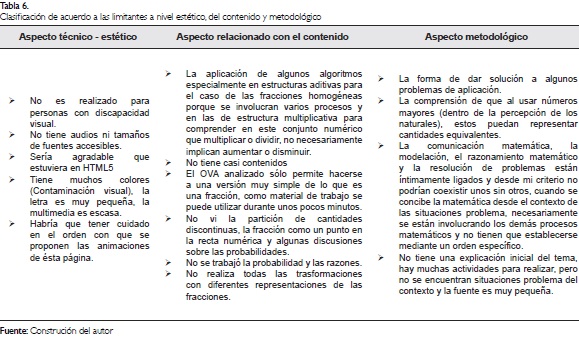
Con relación a las limitaciones detectadas en los OVA; la pregunta 17 (aplicada a cada OVA) mostró que los profesores centran su atención en diferentes aspectos del campo de aplicación del recurso. En la Tabla 6 se sintetizan los aspectos más recuerrentes.3.2.4. Categoría de usos e implementación de los OVA
Esta categoría hace alusión a los aspectos relacionados con la frecuencia de uso de las TIC, el por qué y cómo se usan en el aula y los procesos generales que el OVA permite desarrollar y/o trabajar.
Todos los profesores manifestaron implementar las TIC en el aula (pregunta 6), aunque con una frecuencia diferenciada, es decir, en este caso se encontró que algunos las usan a diario, otros las utilizan semanal o eventualmente cuando las necesitan. A través de la entrevista se pudo colegir que para Erick, Luisa, Andrés y Yulian, la periodicidad de uso no era un aspecto relevante; más allá de ello, resaltaban que era el tema específico quien determina si había o no necesidad de utilizar OVA.
Luego de diligenciar el instrumento "Valoración de Objetos Virtuales de Aprendizaje (OVA) para la enseñanza de las fracciones" que permitió el establecimiento de las características de un instrumento de valoración de OVA, para la enseñanza de un tema en específico de las matemáticas los profesores, a través de este pudieron identificar los procesos generales que tienen que ver con el aprendizaje en el área de matemáticas y que se pueden desarrollar en los OVA. Las consideraciones dadas por los profesores (Erik, Yulian y Andrés) al momento de diligenciar el instrumento permitieron evidenciar que éstos identificaron en mayor medida la utilización de diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista, es decir, dominar con fluidez diversos recursos y registros del lenguaje cotidiano y de los distintos lenguajes matemáticos.
El establecimiento de las características de valoración de OVA planteados en el Instrumento, posibilitaron a los profesores identificar que permiten dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y por qué usarlos de manera flexible y eficaz, vinculando la habilidad procedimental con la comprensión conceptual que fundamenta esos procedimientos, por ejemplo como lo manifestó el profesor Andrés cuando dice que "Podríamos resolver problemas de reparticiones de terrenos, donde los alumnos realizaran trasformaciones de diferentes representaciones de las fracciones, para solucionar cada indicador del problema" lo que permite validar la importancia de la relación que debe existir entre el conocimiento pedagógico y tecnológico del contenido, como se planteó en el marco teórico de este trabajo investigativo.
Y, finalmente, se logró el establecimiento de las características de un instrumento didáctico-conceptual a través de las cuales el profesor pudo valorar el uso de OVA en la enseñanza de las matemáticas, estructurando sus dimensiones, dándole la posibilidad de una participación activa a este último quien es en definitiva el encargado de utilizar la tecnología en contenidos específicos, desarrollando un potencial con argumentos sólidos sobre este proceso de integración y donde desde la selección del OVA se esté realizando una integración de los tres aspectos: contenido, pedagogía y tecnología.
4. Conclusiones
La literatura internacional ha puesto en evidencia la necesidad de aportar a la formación de profesores, de tal manera que integren tecnologías sin caer en el instrumentalismo tecnológico que impida que el profesor utilice las TIC con una intencionalidad definida para favorecer los procesos de enseñanza en el aula de clase. Para atender a esta necesidad, algunas investigaciones se han enfocado en el diseño de instrumentos que aporten criterios para valoración de recursos tecnológicos en el aula de clase; sin embargo, como se argumentó en este artículo, la mayoría de estas investigaciones han aportado a la valoración de aspectos técnicos y estéticos sin entrar en detalle en los aspectos didácticos y del contenido específico de la disciplina en la cual se usa la tecnología.
La investigación que se reporta en este artículo muestra que para diseñar un instrumento que aporte a los profesores criterios de selección de OVA, se requiere de la conjunción de un conjunto de categorías, entre ellas, formativa, didáctica, conceptual, uso e implementación. La conjunción de estas dimensiones muestra la importancia de ello para la formación de profesores, porque no se agota en un listado de aspectos generales, propuestos en una simple lista de chequeo, sino que aporta al conocimiento pedagógico y tecnológico del contenido que tiene el profesor. En el caso particular de los profesores que participaron de este estudio, el instrumento aportó a su conocimiento pedagógico y tecnológico de las fracciones, puesto que permitió una participación activa en la construcción del instrumento, aportó en lo tocante al contenido específico y la forma de abordar este con tecnología, ayudó a identificar la disyunción entre el conocimiento pedagógico y el conocimiento tecnológico del contenido, y a construir reflexiones en los profesores para ver que esa relación debe ser más fuerte y no sea obviada en el aula, además generó espacios de reflexiones para el profesor sobre sus procesos de enseñanza en el aula y posibilitó la toma de decisiones para la selección o no del material a emplear al momento de implementar las TIC.
En este sentido, la presente investigación cobró validez al diseñar el componente didáctico-conceptual del instrumento de valoración nombrado "Valoración de Objetos Virtuales de Aprendizaje (OVA) para la enseñanza de las fracciones", llenando así algunos de los vacíos ya mencionados, en cuanto a la falta de participación del profesor en el proceso de selección de material digital y a su vez dando respuesta al objetivo general de la presente investigación. El instrumento diseñado tuvo como propósito principal brindar a los profesores herramientas para la selección de OVA en la enseñanza de temas específicos del área de matemáticas (fracciones), en donde las características de un instrumento construido fueron encaminadas hacia aspectos relacionados con el conocimiento pedagógico y tecnológico del contenido que debe tener el profesor, buscando la constante relación entre estos tres aspectos básicos de la enseñanza.
Las características del instrumento de valoración de OVA, le permitieron al profesor una participación evidenciada en la confrontación de sus conocimientos y los conocimientos de porqué y para qué usar las OVA; lo cual a su vez, supera la visión de instrumento como lista de chequeo para ubicarse en un ejercico reflexivo y analítico, que basado en sus conocimientos específicos del área de matemáticas y en su experiencia como docente de aula, aportó a la construcción de argumentos para la elección e integración de ellos en la enseñanza de las fracciones, ya que se generaron espacios de reflexión donde los profesores identificaron su visión sobre la integración de las TIC en el aula de clase y cómo estas responden al reto del uso de recursos tecnológicos como los OVA con criterios pedagógicos claros. Además, se orientó al profesor sobre la importancia de conocer el contenido a enseñar, al igual que otros procesos que debe tener en cuenta para llevar a cabo los procesos de enseñanza mediados con tecnología.
El instrumento diseñado aportó a la formación del profesor en su criterio para la integración de OVA, como apoyo de los procesos de enseñanza en el área de matemática; un instrumento que puso de manifiesto las ventajas de la utilización de las TIC para la enseñanza de determinado contenido matemático y que finalmente permitió esa relación importante de la que se habló en el marco teórico de la presente investigación.
Esta investigación aporta en el sentido que abre espacios de reflexión en la comunidad de profesores, ya que permitió mostrar la importancia que tiene la correcta selección de los materiales a ser implementados en el aula de clase y la implicación que tiene dicha selección en los procesos de enseñanza llevados a cabo por el mismo. En este sentido, un profesor de matemáticas debe ser consciente de la importancia de su formación continua y constante en aspectos como el conocimiento pedagógico y tecnológico del contenido y nuevamente la relación que debe existir entre estos tres aspectos.
Finalmente, este proceso investigativo deja abiertas otras líneas de investigación referidas a la importancia de las características de un instrumento de selección de OVA para otros contenidos del área de matemáticas y por qué no, de otras áreas, abriendo así la posibilidad de llenar algunos de los vacios existentes como los referidos a la existencia de instrumentos de valoración para temáticas específicas, teniendo en cuenta que un instrumento diseñado para valorar otro tema específico de las matemáticas, requeriría de la reestructuración de la que fue llamada dimensión conceptual y tal vez un redireccionamiento de los enfoques de las otras tres dimensiones.
Conflicto de intereses
Los autores declaran no tener ningún conflicto de intereses.
Referencias bibliográficas
1. ALVES-MAZZOTTI, Alda Judith; GEWANDSZNAJDER, Fernando. O método nas ciencias naturais e sociais: pesquisa quantitativa e qualitativa. Sao Paulo: Pioneira, 2000. P:107-188. [ Links ]
2. ANDRADE-ARÉCHIGA, María; LÓPEZ, Gilberto; LÓPEZ-MORTEO, Gabriel. Assessing effectiveness of learning units under the teaching unit model in an undergraduate mathematics course. En: Computers & Education, 2012. vol. 59, no 2, p. 594-606. [ Links ]
3. ANGELI, Charoula; VALANIDES, Nicos. Epistemological and methodological issues for the conceptualization, development, and assessment of ICT-TPCK: Advances in technological pedagogical content knowledge (TPCK). Computers & Education, 2009, vol. 52, no 1, p. 154-168. [ Links ]
4. BALL, Deborah Loewenberg; THAMES, Mark Hoover; PHELPS, Geoffrey. Content knowledge for teaching what makes it special?. Journal of teacher education, 2008, vol. 59, no 5, p. 389-407. [ Links ]
5. BORBA, Marcelo C.; ARAÚJO, Jussara de Loiola. Pesquisa qualitativa em educação matemática. Belo Horizonte: Autêntica Editora, 2004. 120p. [ Links ]
6. BORBA, Marcelo C.; VILLARREAL, Mónica E. Humans-with-media and the reorganization of mathematical thinking: Information and communication technologies, modeling, visualization and experimentation. New York: Springer Science & Business Media, 2006. 230p. [ Links ]
7. BORBA, M. de C.; SCUCUGLIA, RRS; GADANIDIS, George. Fases das Tecnologias Digitais em Educação Matemática: sala de aula e internet em movimento. Belo Horizonte: Autêntica, 2014. 149 p. [ Links ]
8. CABERO-ALMENARA, Julio; HUEROS, Ana Duarte. Evaluación de medios y materiales de enseñanza en soporte multimedia. En: Pixel-Bit: Revista de medios y educación, 1999. no 13, p. 3. [ Links ]
9. CASILIMAS, Carlos A. Sandoval. Investigación cualitativa. Icfes, 1996. [ Links ]
10. CASTILLO, Sandra. Propuesta pedagógica basada en el constructivismo para el uso óptimo de las TIC en la enseñanza y el aprendizaje de la matemática. Revista latinoamericana de investigación en matemática educativa, 2008, vol. II, no 2, p. 171-194. [ Links ]
11. CHIAPPE LAVERDE, Andrés. Acerca de lo pedagógico en los objetos de aprendizaje-reflexiones conceptuales hacia la construcción de su estructura teórica. Estudios pedagógicos (Valdivia), 2009, vol. 35, no 1, p. 261-272. [ Links ]
12. COLOMBIA. MINISTERIO DE EDUCACIÓN NACIONAL. Lineamientos Curriculares para el área de Matemáticas (1998). Bogotá D.C.: Magisterio, 1998. 131p. [ Links ]
13. CUADRADO-GALLEGO, Juan J. Adaptación de las Métricas de Reusabilidad de la Ingeniería del Software a los Learning Objects. Revista de Educación a Distancia, 2005. 8p. [ Links ]
14. FIGUEROA, María Antonieta Abud. Calidad en la Industria del Software. La Norma ISO-9126. UPIICSA, 2005. [ Links ]
15. GRAELLS, Pedro Marqués. Evaluación y selección de software educativo. Las nuevas tecnologías en la respuesta educativa a la diversidad, Universidad Autónoma de Barcelona. 2002, p. 115. [ Links ]
16. GRAHAM, Charles R. Theoretical considerations for understanding technological pedagogical content knowledge (TPACK). Computers & Education, 2011, vol. 57, no 3, p. 1953-1960. [ Links ]
17. GROSSMAN, Pamela Lynn. The making of a teacher: Teacher knowledge and teacher education. Teachers College Press, Teachers College, Columbia University, New York 1990. [ Links ]
18. HADJERROUIT, Said. A conceptual framework for using and evaluating web-based learning resources in school education. En Journal of Information Technology Education Volume 9, 2010. [ Links ]
19. JANG, Syh-Jong; CHEN, Kuan-Chung. From PCK to TPACK: Developing a transformative model for pre-service science teachers. Journal of Science Education and Technology, 2010, vol. 19, no 6, p. 553-564. [ Links ]
20. KOEHLER, Matthew J.; MISHRA, Punya; YAHYA, Kurnia. Tracing the development of teacher knowledge in a design seminar: Integrating content, pedagogy and technology. Computers & Education, 2007, vol. 49, no 3, p. 740-762. [ Links ]
21. LINCOLN, Yvonna S.; GUBA, Egon G. Naturalistic inquiry. Sage, 1985. [ Links ]
22. MISHRA, Punya; KOEHLER, Matthew. Technological pedagogical content knowledge: A framework for teacher knowledge. The Teachers College Record, 2006, vol. 108, no 6, p. 1017-1054. [ Links ]
23. MORALES, Erla, et al. Propuesta de evaluación de objetos de aprendizaje. En II Simposio Pluridisciplinar sobre Diseño, Evaluación y Descripción de Contenidos Educativos, SPEDECE. 2005. [ Links ]
24. NARDONI, Marta Graciela; POCHULU, Marcel David. La comprensión que tienen los alumnos referida a números racionales, como objeto matemático, al terminar la escuela secundaria. En memorias congreso internacional didáctica de la matemática. Coleccion compilaciones 01. Santa Marta, Colombia 2015. p. 107. [ Links ]
25. OLIVEIRA, Franciele. A inviabilidade do uso das tecnologias da informacao e comunicacao no contexto escolar: o que contam os professores de matemática?. Trabajo de grado de maestría en Educación Matemática. Rio Claro-SP.: Universidade Estadual Paulista. Instituto de Geociencias e Ciencias Exatas, 2014. 169p. [ Links ]
26. PAULSSON, F.; NAEVE, A. Establishing technical quality criteria for Learning Objects, Media technology and graphic arts. 2006. [ Links ]
27. REEVES, T. Evaluating what really matters in computer-based education. Retrieved 25 May, 2005. 1997. [ Links ]
28. SHULMAN, Lee S. Those who understand: Knowledge growth in teaching. Educational researcher, 1986, vol. 15, no 2, p. 4-14. [ Links ]
29. SHULMAN, Lee. Knowledge and teaching: Foundations of the new reform. Harvard educational review, 1987, vol. 57, no 1, p. 1-23. [ Links ]
30. SMITH, Gordon V. y PARR, Russell L. Market and cost approaches. En: Valuation of intelectual property and intagible assets. 3 ed. New York: Jhon Wiley, 2000. P. 175-21. [ Links ]
31. SQUIRES, David; PREECE, Jenny. Predicting quality in educational software: Evaluating for learning, usability and the synergy between them. Interacting with computers, 1999, vol. II, no 5, p. 467-483. [ Links ]
32. TRIANA, Mónica; CEBALLOS, Juan. Valoración de Objetos Virtuales de Aprendizaje para la enseñanza de las matemáticas. Instrumento para profesores. Tesis de maestría no publicada, Universidad de Medellin. Medellín (Colombia). 2015. [ Links ]
33. VARGO, John, et al. Learning object evaluation: computer-mediated collaboration and inter-rater reliability. International Journal of Computers and Applications, 2003, vol. 25, no 3, p. 198-205. [ Links ]
34. VELÁZQUEZ, César E., et al. La determinación de la calidad de objetos de aprendizaje. VII Encuentro Internacional de Ciencias de la Computación ENC, 2006, vol. 2006, p. 346-351. [ Links ]
35. VIDAL, Christian L.; SEGURA, Alejandra A.; PRIETO, Manuel E. Calidad en objetos de aprendizaje. En Memorias V Simposio Pluridisciplinar sobre Diseño y Evaluación de Contenidos Educativos Reutilizables, SPEDECE08. Salamanca (España). 2008. [ Links ]
36. VILLA-OCHOA, Jhony Alexander; GALVIS, Jackeline; SIERRA, Ruben; VELEZ, Lida. Integración de tecnologías en el aula de clase. El caso de los profesores implicados en el proyecto Teso. En: Tecnologías Digitais en Educação: perspectivas teóricas e metodológicas sobre formação e prática docente. Curitiba: Editora CRV. P 35-56. [ Links ]
37. VILLA-OCHOA, Jhony Alexander; VÉLEZ, Lida; ROJAS, Carlos; BORBA, Marcelo. Visualización de conceptos matemáticos: Geogebra en la reorganización de los modos de producción de conocimiento matemático. En: Una visión de las Ciencias Básicas. Modelación y Formación aplicada a casos reales. Medellín: Sello Editorial Universidad de Medellín. P. 65-80. [ Links ]
38. VILLODRE, Silvia; LLARENA, Myriam G. Objetos de Aprendizaje: Criterios de diseño y uso. En VI Congreso de Tecnología en Educación y Educación en Tecnología. 2011. [ Links ]
39. WONG, Khoon Yoong, et al. The preparation of primary mathematics teachers in Singapore: programs and outcomes from the TEDS-M study. ZDM, 2012, vol. 44, no 3, p. 293-306. [ Links ]