1. Introduction
Structural control systems have turned into a standard technology to improve the dynamic response of civil engineering structures under dynamic actions such as wind, waves, explosions, and earthquakes (Buckle, 2000). Control systems are typically grouped into: passive, active, hybrid, and semiactive. Moreover, passive systems are widely accepted by the engineering community because of their mechanical simplicity, low power requirements, and controllable force capacity (Spencer and Nagarajaiah, 2003).
Into passive systems, Tuned Mass Dampers (TMDs) have been tested widely by the engineering community throughout the years. Introduced originally by Frahm (1911), the TMD links an additional mass to the main structure using a spring and a viscous damper, both tuned optimally to transfer energy among the vibrating modes (Cimellaro and Marasco, 2018). To achieve the tuning of the TMD to the fundamental frequency of the structural system, the optimal design parameters of the device must be found. Based on the transfer function fixed-points theory, Ormondroyd (1928) proposed expressions for the optimum frequency and damping ratios, idealizing a two-degree of freedom model consisting of the main structure with no damping and TMD, and simulating the dynamic action as a harmonic excitation. Later, Warburton (1981; 1982) proposed expressions for the same parameters considering white noise excitations. Based on these studies, Sadek, Mohraz, Taylor, Chung (1997) developed closed form expressions for the frequency and damping ratios of the TMD, analyzing the frequency domain, and considering damping associated with the main structure.
The first full-scale implementations of TMDs were aimed to control the displacement caused by wind-induced vibrations. In that sense, TMDS have been deployed in several structures around the world including the Centre Point Tower in Sydney; the Citicorp Center in New York; the Chiba port tower in Japan; and more recently, the CN tower in Canada and the Taipei 101 tower in Taiwan (Holmes, 1995; Soto and Adeli, 2013). Multiple approaches based on the conventional TMD have been applied thereafter. Among them, pendulum TMDs (Gerges and Vickery, 2005; Setareh, Ritchey, Baxter, Murray, 2006); tuned liquid column dampers (Di Matteo, Furtmüller, Adam and Pirrotta, 2018); and bidirectional TMDs (Almazán et al. 2007). Nonetheless, some early investigations concluded that TMDs were not effective in reducing the response of buildings subjected to seismic excitation (Kaynia, Biggs and Veneziano, 1981; Sladek and Klinger, 1983) which was due to two principal reasons. First, the limitation associated with the amount of mass added to the structural system, and more importantly, that conventional tuning methodologies were not capable of reducing the vibration at the higher modes, which were affected by the wide spectrum of frequency components that characterized earthquake ground motions.
To address the last-mentioned problem, since early 2000s numerical iterative methods have been employed to carry out the tuning process of TMDs. Conventional numerical techniques have been used for that purpose such as numerical minimax optimization (Salvi and Rizzi, 2015). Moreover, metaheuristic methodologies have been effective in solving the tuning problem of TMDs such as, particle swarm optimization (Leung et al., 2008; Leung and Zhang, 2009), harmony search (Bekdas and Nigdeli, 2011; 2013), ant colony (Farshidianfar and Soheili, 2011), flower pollination algorithm (Nigdeli et al., 2017) bat algorithm (Bekdas, Nigdeli and Yang, 2018), and cuckoo search (Etedali and Rakhshani, 2018). Artificial intelligence-based approaches have also been employed for optimization strategies: genetic algorithms (Pourzeynali, Salimi, Kalesar, 2013), and more recently fuzzy logic combined with machine learning (Yucel, Bekdas, Nigdeli and Sevgen, 2019).
In that sense, this study presents a methodology for the optimal design of passive Tuned Mass Dampers (TMDs) located at upper levels of high-rise buildings to control its dynamic response under earth-quake excitations. The selection process of the optimal design parameters is carried out through a novel metaheuristic approach based on the differential evolution method (DE) (Storn and Price, 1997). The algorithm is aimed to reduce the maximum horizontal peak displacement of the structure and the root mean square (RMS) response of displacements as well. Moreover, four objective functions derived from multiple weighted linear combinations of the two previously mentioned parameters are also studied to obtain the most efficient TMD design configuration.
A parallel process based on an exhaustive search (ES) with precision to 2 decimal positions is used to validate the optimization methodology based on DE. The proposed methodology is applied to a 32-story case study derived from an actual building structure and subjected to different ground acceleration registers. The best dynamic performance of the building is observed when the greatest weight is given to the RMS response of displacement in the optimization process. The results of the study show a large enhancement in the dynamic response of the building controlled by the optimized TMDs, achieving reductions in the maximum floor displacements of up to 43%, and RMS values of displacement of up to 52% in the case study building.
Tuned Mass Dampers (TMDs)
Conventional mathematical formulation
The design process of TMDs is typically associated with the searching of the optimal frequency ratio (f), the damping ratio (ζd) and the mass ratio (μ), represented respectively by Equation (1), (2) and (3):
where ω d, ω 1, k d, m d, c d and m s are the optimum frequency of the TMD, the fundamental circular frequency of the main structure, the TMD stiffness coefficient, the TMD mass, the TMD damping coefficient and the total mass of the structure, respectively.
These parameters are deduced from a linear system in which the main structure is simplified as a single degree-of-freedom (SDOF) system, as illustrated in Figure 1.
where k s, c s, are the stiffness coefficient and damping coefficient of the main structure idealized as a SDOF system, and besides, x s and x d are the displacement response of the main structure and the TMD, respectively.
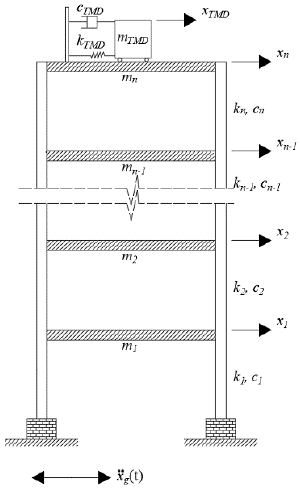
Mathematical model of a n-degree-of-freedom system equipped with a TMD at the top floor
The equations of motion that govern the behavior of the n-degree-of-freedom structural system equipped with a TMD located at the top floor of the building are deduced from the scheme presented in Figure 2. Here the displacement at each story-level is represented by x i, while the stiffness, damping, and mass coefficients at each story-level of the building are defined as k i, c i, and m i, respectively. Besides, the TMD action is introduced as an extra degree of freedom represented by x TMD, as the stiffness, damping, and mass parameters are identified as k TMD, c TMD, and m TMD, respectively.
Source: Authors.
Figure 2 Representation of a structural system of n degrees of freedom equipped with a TMD at the top floor.
Subsequently, the structural system controlled via TMD can be modeled as a set of n+1 degrees of freedom, whose equation of motion can be expressed as:
where x(t), ẋ(t), and ẍ(t) are the n+1 order vectors of displacement, velocity, and acceleration of the system; 1 is a unit vector, and ẍ g(t) denotes the ground acceleration over time. On the other hand, the matrices M, C, and K represent, the mass, damping, and stiffness matrices of the system, which can be expressed as:
Now, the equation of motion of the system is modified to a space-state representation to determine the dynamic response of the linear system. Thus, the state vector z(t) is introduced as:
The above-mentioned vector involves the displacements and velocities of the controlled system. By deploying Equation (4), it may be written the state-space representation of the structural system controlled by TMD:
where 0 and I denote a zero matrix and an identity matrix, respectively. Subsequently, Equation (9) is rewritten as:
where A represents the transition state matrix, and B the location adjustment matrix of the external excitation in the structural system:
Description of the TMD design parameters optimization methodologies
A metaheuristic optimization algorithm based on DE is used to obtain the optimal design parameters of the TMD system. Subsequently, the results are validated through an exhaustive search (ES) optimization procedure with precision to 2 decimal positions. The main purpose of the ES validation is to assess the feasibility of the DE to determine reliable results for the optimal TMD parameters.
Furthermore, six objective functions are proposed in the optimization process to diminish the dynamic response of the structure equipped TMD system, when it is subjected to seismic excitations. These functions are associated with the reduction of the maximum horizontal peak of displacement of the structure, and the reduction of the Root Mean Square (RMS) values of displacements. The use of multiple functions aims to determine which of these objective functions is more efficient, based on the evaluation and comparison of the decrease in the response of both parameters previously mentioned.
In that sense, the objective functions OA1 and OA2 correspond to the reduction of the maximum horizontal peak displacement in the entire structure, and the decrease in the RMS values of displacements, respectively:
Regarding the remaining four objective functions, these are defined as a variable weighted linear combination of the relationships between the above-mentioned parameters in Equation (13) and Equation (14). These functions are defined as J1, J2, J3, and J4 and described through Equation (15):
Differential Evolution-based optimization
Differential evolution (DE) is a simple and efficient metaheuristic, focused on the optimization problem of real variables in continuous fields. The original idea was introduced by Storn and Price (1997) as part of evolutionary computing. It requires little or no parameter tuning and usually presents a fast convergence speed. DE strategy is based on a population evolutionary algorithm, which utilizes an amount NP of D-dimensional parameter vectors as a population for each generation. The initial vector population is chosen randomly and should cover the entire parameter space. DE generates new mutated parameter vectors by adding the weighted difference between two population vectors to a third vector. Then, the mutated vector parameters are mixed with the parameters of another predetermined target vector, to generate a trial vector, this operation is referred to as crossover. If the trial vector produces a lower cost function value than the target vector, the trial vector replaces the target vector in the subsequent generation.
Exhaustive search-based optimization validation
An optimization process based on exhaustive search (ES) with precision to 2 decimal positions is developed to validate the results obtained by using the DE-based optimization process. The ES process aims to determine the optimal design parameters through a comparative analysis of the controlled dynamic response system for each possible combination of parameters. Considering a fixed μ value, the algorithm selects initial values of ζd and f inside the search domains established in Equation (16), and Equation (17).
Subsequently, the m TMD’ c TMD, and k TMD coefficients are determined. Next, the structure equipped with the selected TMD is subjected to the earthquake excitations and the response values are stored for later processing in the objective functions that are intended to be minimized. The optimization problem continues until all possible combinations of parameters μ, ζ d and f are tested. Finally, a comparative analysis is carried out considering all the analyzed TMD configurations in order to establish which is the optimal TMD configuration.
Numerical example
In this section the proposed methodology is applied to a 32-story case-study derived from an actual building currently under construction in Medellin city, Colombia. The structure presents a total elevation of 97 m, and the lateral force-resisting system consists on resistant moment frames. Additionally, the building has an irregular L-shape configuration in-plan, which makes it more vulnerable to seismic damage; a complete characterization of the case-study is provided by Caicedo, Lara-Valencia, Blandon, Graciano (2021).
Benchmark records
Prieta
In order to carried out the optimization process described deeply in section 3, and to evaluate the dynamic performance of the case-study building in the linear-elastic range, four well-known accelerograms of recorded earthquakes are taken from the Pacific Earthquake Engineering Research (PEER) Centre database. The records are labeled and described in Table 1.
Table 1 Characterization of the benchmark records.
| Record | Event Name | Station | Component | PGA [g] | Duration [s] |
|---|---|---|---|---|---|
| 1 | El Centro | El Centro | S00E | 0.35 | 53.73 |
| 2 | Kobe | Takatori | 000 (CUE) | 0.61 | 30.03 |
| 3 | Loma Prieta | Capitolia | 90 DEG | 0.40 | 39.98 |
| 4 | Northridge | Rinaldi | S49W | 0.84 | 14.97 |
Source: Authors.
Because of its dynamic characteristics, these accelerograms are expected to have a great impact on the seismic behavior of the case-study building. Therefore, they will be used as input excitations in the case-study building to determine the optimally set of f and ζ d parameters in both, the DE methodology and the ES process. Subsequently, the dynamic behavior of the building under such excitations will be detailed reported.
Optimization results
Table 2 compares the design parameters of TMDs obtained through the DE-based optimization and the results computed by the ES-based methodology, considering OA1 and OA2 objective functions, and μ ratios of 0.02 and 0.05. And Table 3 shows ζ d and f parameters derived from J1, J2, J3, and J4 approaches.
Table 2 TMD design parameters optimized by objective function OA1 and OA2.
| μ=0.02 | μ=0.05 | |||||||
|---|---|---|---|---|---|---|---|---|
| Earthquake | DE | ES | DE | ES | ||||
| ζ d | f | ζ d | f | ζ d | f | ζ d | f | |
| OA1 | ||||||||
| El Centro | 0.48 | 2.00 | 0.50 | 2.00 | 0.40 | 2.00 | 0.39 | 2.00 |
| Kobe | 0.01 | 0.95 | 0.00 | 0.94 | 0.36 | 1.40 | 0.35 | 1.38 |
| Loma Prieta | 0.03 | 1.09 | 0.01 | 0.96 | 0.20 | 0.89 | 0.16 | 0.89 |
| Northridge | 0.50 | 2.00 | 0.50 | 2.00 | 0.00 | 1.21 | 0.50 | 2.00 |
| OA2 | ||||||||
| El Centro | 0.21 | 0.90 | 0.18 | 0.91 | 0.33 | 0.98 | 0.34 | 0.98 |
| Kobe | 0.07 | 1.01 | 0.07 | 1.00 | 0.18 | 1.01 | 0.17 | 1.01 |
| Loma Prieta | 0.13 | 0.93 | 0.1 | 0.9 | 0.16 | 0.86 | 0.14 | 0.86 |
| Northridge | 0.14 | 0.93 | 0.12 | 0.92 | 0.22 | 0.84 | 0.22 | 0.83 |
Source: Authors.
Table 3 TMD design parameters optimized by objective function J1, J2, J3 and J4.
| μ=0.02 | μ=0.05 | |||||||
|---|---|---|---|---|---|---|---|---|
| Earthquake | DE | ES | DE | ES | ||||
| ζ d | f | ζ d | f | ζ d | f | ζ d | f | |
| J1 | ||||||||
| El Centro | 0.22 | 0.94 | 0.21 | 0.93 | 0.35 | 1.03 | 0.35 | 1.02 |
| Kobe | 0.07 | 1.01 | 0.07 | 1.00 | 0.18 | 1.01 | 0.18 | 1.01 |
| Loma Prieta | 0.11 | 0.94 | 0.09 | 0.91 | 0.18 | 0.85 | 0.16 | 0.89 |
| Northridge | 0.14 | 0.93 | 0.12 | 0.93 | 0.22 | 0.84 | 0.22 | 0.84 |
| J2 | ||||||||
| El Centro | 0.33 | 0.98 | 0.31 | 0.98 | 0.37 | 1.06 | 0.36 | 1.08 |
| Kobe | 0.10 | 1.04 | 0.07 | 1.00 | 0.22 | 1.03 | 0.2 | 1.01 |
| Loma Prieta | 0.06 | 0.95 | 0.08 | 0.93 | 0.18 | 0.85 | 0.16 | 0.89 |
| Northridge | 0.10 | 0.93 | 0.12 | 0.93 | 0.23 | 0.86 | 0.22 | 0.85 |
| J3 | ||||||||
| El Centro | 0.50 | 1.22 | 0.5 | 1.27 | 0.41 | 1.17 | 0.42 | 1.19 |
| Kobe | 0.10 | 1.04 | 0.06 | 0.99 | 0.31 | 1.03 | 0.27 | 1.01 |
| Loma Prieta | 0.06 | 0.95 | 0.06 | 0.95 | 0.20 | 0.89 | 0.16 | 0.89 |
| Northridge | 0.10 | 0.93 | 0.12 | 0.94 | 0.20 | 0.89 | 0.23 | 0.87 |
| J4 | ||||||||
| El Centro | 0.48 | 1.99 | 0.5 | 2 | 0.41 | 1.98 | 0.42 | 2 |
| Kobe | 0.01 | 0.95 | 0.03 | 0.98 | 0.48 | 1.19 | 0.48 | 1.18 |
| Loma Prieta | 0.02 | 0.95 | 0.03 | 0.99 | 0.20 | 0.89 | 0.16 | 0.89 |
| Northridge | 0.13 | 0.99 | 0.11 | 0.97 | 0.22 | 0.94 | 0.23 | 0.93 |
Source: Authors.
As expected, the results computed by the DE-based methodology show correspondence with the results computed through the ES process. Differences were observed from the third decimal position, which have no impact on the global response of the structure. Regarding the design parameters, the optimal values of ζ d vary between 0.01 and 0.13, and the optimal f ratios oscillate from 0.9 to 1.0. Figure 3 depicts the dispersion of optimal design values derived from the two optimization methodologies and the six objective functions used in this investigation.
2. Results, analysis and discussion
Now, the seismic performance of the building is evaluated under the action of the four seismic records used in the optimization process. It is worth noting that the scope of this investigation is limited to the linear behavior of the structural system. Thus, the numerical model does not take into account any type of damage or yielding process affecting the structure. Furthermore, the displacements obtained are presumable within the elastic behavior of the system.
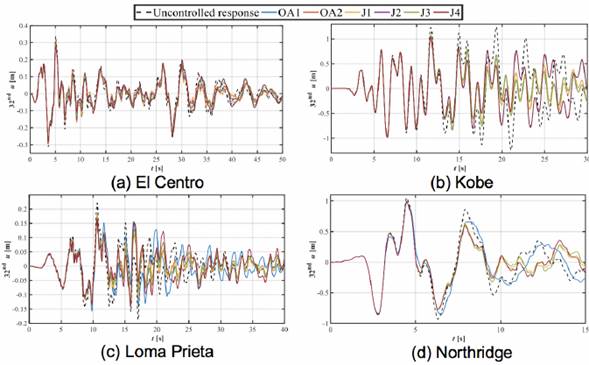
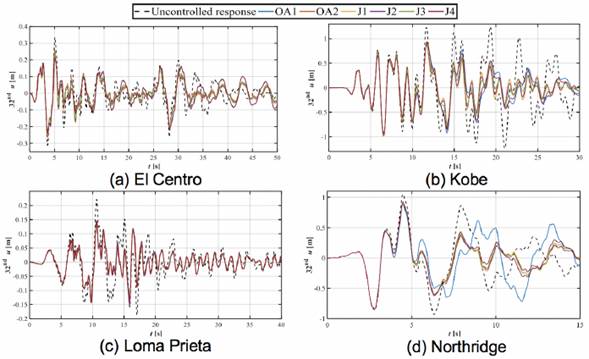
Figure 4 and Figure 5 show the time-history of displacements at the 32nd story of the building, for μ = 0.02 and 0.05, respectively. Even though both TMD options (μ = 0.02, and 0.05) can effectively reduce the dynamic response of displacements, it is visibly clear that TMDs with μ = 0.05 reach greater reductions in lateral displacements at the upper level of the structural system regardless the objective function.
Source: Authors.
Figure 4 Displacement of the 32nd story of the structure equipped with TMDs with μ=0.02.
Source: Authors.
Figure 5 Displacement of the 32nd story of the structure equipped with TMDs with μ=0.05.
The controlled response of the structure using optimally designed TMDs with μ = 0.05 is remarkable. The best performance is achieved with devices optimized through OA1 and J4 approaches, showing reductions of up to 43% and 42%, respectively. Nevertheless, the reductions in the maximum displacements at each floor achieved by the devices designed with the remaining objective functions are notable as well, exhibiting reductions up to 39%, 38%, 38% and 40% for the cases of optimization OA2, J1, J2, and J3, respectively. The smallest reductions were obtained by using the Northridge acceleration record; these reductions ranged from 12% to 17%. Furthermore, for the three remaining accelerograms, the reduction of displacements at the 32nd oscillates between 20% and 43%.
The greatest reductions in the RMS displacements at the roof level of the structure are obtained when the building is equipped with μ = 0.05 TMDs. These reductions are attained using the OA2 and J1 approaches: 20.19%, 42.76%, 33.23%, and 26.35% for the El Centro, Kobe, Loma Prieta, and Northridge accelerograms, respectively. Clearly, the dynamic response observed by minimizing the RMS response of displacement at the top floor of the structure depicts a much more uniform and efficient behavior than the reductions of the maximum horizontal peak floor displacements, especially with objective functions OA2 and J1.Using the Kobe and Northridge records, the results report the highest response magnitudes, and at the same time the TMDs exhibit the greatest performance. This behavior indicates that the objective functions for the optimal design of TMDs should be focused on minimizing the RMS values of displacements, or instead a linear combination in which the greatest weight should be given to this parameter. Hence, the numerical results demonstrate that objective functions OA2, J1, and J2 lead to the most efficient design parameters for TMDs.
Consequently, the devices designed through these objective functions are the ones that best improve the seismic performance of the building. Moreover, the TMDs designed through OA2, J1, and J2 demonstrates that the control of the RMS values of displacements in the structure is the best possible within both evaluated parameters, which implies significant reductions in the dynamic response over time. Moreover, the horizontal peak response of displacements is markedly reduced as well. Hence, according to these results, it is demonstrated that the objective function J1 is the most balanced and effective among the six objective functions analyzed in this paper, despite the small differences in performance with OA2 and J2.
3. Conclusions
In this study, a methodology for the selection of optimal design parameters of TMDs based on DE to reduce the dynamic response of buildings subjected to seismic excitations was presented. Six different objective functions were proposed to be minimized in the DE-based algorithm. These functions depend on the reduction of the maximum horizontal peak displacement of the structure, the RMS response of displacements, and four more weighted linear combinations of the two previously mentioned parameters. A process based on an exhaustive search (ES) with precision to 2 decimal positions was used to validate the DE-based optimization. The proposed methodology was applied to a 32-story case-study derived from an actual building structure and subjected to different ground acceleration registers. According to the numerical analysis on the seismic dynamic behavior of the building in the linear-elastic range, it may be concluded that the optimization approach J1, lead to the most efficient and balanced design configuration of TMD systems, despite the small differences in performance with OA2 and J2. Furthermore, the proposed the tuning technique based on DE confirmed to be successful, fast and reliable by achieving reductions in the maximum floor displacements of up to 43%, and RMS values of displacement of up to 52%.




















