1. Introducción
Los impuestos constituyen el principal componente de los ingresos corrientes de un Estado. A través de estos, los gobiernos pueden invertir en educación, salud, infraestructura, seguridad, justicia, entre otros aspectos. En otras palabras, los impuestos son la fuente vital de rentas de los gobiernos y son los que permiten el buen funcionamiento de estos (Hernández Becerril, 2017). En Colombia, con la Constitución del 1991, la creación del situado fiscal y de las participaciones municipales, inicia un proceso de descentralización fiscal. Aunque los ingresos de los gobiernos subnacionales crecieron, al ser una descentralización de tipo no pura, los gobiernos locales no pueden crear impuestos, y es el gobierno central quien decide y dispone el uso de los recursos que envían (Bonet, 2004; Cante, 2009).
Ante la imposibilidad de crear nuevos tributos, los gobiernos locales deben implementar estrategias que les permitan aumentar el recaudo. Es por ello, que los gobiernos subnacionales trabajan con el propósito de generar una cultura tributaria y ganarse la confianza de los contribuyentes o realizan descuentos y promociones para incrementar los pagos.
En particular, en la ciudad de Cartagena, cuya política tributaria está regida por el acuerdo 045 del 2006, y en los aspectos relacionados con el impuesto predial, en consonancia con las leyes 14 de 1983, 44 de 1990, 1995 de 2019 y 601 del 2000, uno de los tributos más importante es el impuesto predial unificado. Este impuesto representó un 42% de los ingresos tributarios recaudados en el periodo 2000-2019. Por esto y dada su importancia en los ingresos de la ciudad, este documento toma los postulados de la nueva geografia económica y sus autores investigan si existe influencia del espacio en el pago del impuesto predial de los barrios de la ciudad de Cartagena, con el objetivo de identificar las aglomeraciones espaciales y la influencia que estas tienen sobre el pago del impuesto predial unificado.
Para conseguir lo que se expone en líneas anteriores, se calcula el índice de Moran univariado y bivariado para observar la influencia y la significancia, tanto en el espacio como en el tiempo de la ubicación geográfica de los barrios y correspondiente pago del impuesto predial. Los resultados muestran que existen clústeres espaciales respecto al pago del impuesto predial, pues la mayoría de los barrios constituyen aglomerados que realizan un bajo pago promedio, igualmente sucede con sus vecinos. También hay barrios agrupados en zonas donde se paga impuesto predial por encima de la media y tributan altos valores. Así mismo, se encontraron barrios con vecinos que tributan por encima de la media, pero ellos pagan valores por debajo del promedio.
Estos barrios se consideran entidades espaciales, en las cuales se debe actuar y fortalecerlos con proyectos que mejoren la infraestructura económica y social, las condiciones de vida de los habitantes, y vincularlos a estas iniciativas. En efecto, son un gran potencial y habría en ellos un incremento en el nivel de pagos en relación con el impuesto predial. Lo expuesto hace manifiesta la necesidad de plantear nuevas estrategias en aras de mejorar la eficiencia en el recaudo del impuesto predial.
Este documento se estructura de la siguiente manera: inicialmente se presentan los resultados de la revisión de la literatura, luego se describe la metodología utilizada para el cálculo del índice de Moran, seguidamente presenta y discute los resultados alcanzados y finalmente las conclusiones.
2. Marco teórico
En el marco del desarrollo económico local, existen teorías basadas en los factores geográficos, de localización y regionales, las cuales dan soporte a las investigaciones sobre el desarrollo territorial y urbano. Siguiendo el trabajo de (Tello, 2006) algunas de estas teorías son:
2.1. Teoría de la localización
Esta teoría es desarrollada inicialmente en los trabajos realizados por Thünen (1826), Weber (1909), Lösch (1953), North (1955) e Isard (1956). La teoría de la localización estudia la determinación del lugar geográfico de las actividades productivas de bienes y servicios de las empresas. Se explica que para lograr el objetivo de la industrialización en una región se debe pasar por varias etapas. Estas son: de autosubsistencia o autoconsumo, mejoras en el transporte, aumento del comercio, de la población y, por último, las regiones menos desarrolladas alcanzan un estado final de desarrollo en donde se especializan en actividades terciarias de exportación de capital y mano de obra especializada.
En esta teoría se incluye el estudio de las aglomeraciones productivas, las estructuras económicas y sociales de las ciudades, y la asignación de recursos y sus cambios en las regiones (Tello, 2006).
2.2. Teoría de la base económica
Desarrollada por Goodwin (1949) y Metzler (1950), la teoría de la base económica postula que el crecimiento y desarrollo de un área geográfica está determinada en función de la demanda "externa" de bienes y servicios originada fuera de dicha área geográfica. Es decir, explica el crecimiento económico local a partir de los flujos comerciales con el exterior. Lo que impulsa el progreso de la región es el desarrollo de los sectores básicos cuyos productos son demandados fundamentalmente por regiones externas a la ubicación de los sectores básicos.
La presencia de dos grupos de factores específicos son los que determinan el avance de los sectores básicos de la economia. Los primeros son los factores internos de la región como el espacio geográfico y dotación de recursos, la ubicación de la región, la demanda de los bienes y servicios producidos en esta, la producción de bienes y servicios finales, así como la distancia entre estas ubicaciones. Los segundos son los factores externos a la región donde se incluyen aquellos elementos que propician el desarrollo de las otras regiones.
2.3. Teoría de la causación circular y acumulativa
Los trabajos realizados por Myrdal (1957) y posteriormente retomados por Arthur (1989) y Krugman (1991) exponen que las fuerzas del mercado en lugar de corregirse por sí mismas, pueden conducir a la economía a una situación que se perpetúa en el tiempo. Esto indica que un mercado será grande cuando la producción del sector manufacturero esté concentrada. La concentración de la producción y de empresas, usualmente induce a que los costos de producción de los bienes y servicios sean menores en las áreas donde estas se localizan.
En ese sentido Hirschman (1958) formula que a partir de una materia prima se conforman firmas abastecedoras en una región, lo cual es llamado eslabonamiento hacia atrás. Luego se forman firmas industriales, lo cual es conocido como eslabonamiento hacia adelante. La existencia de eslabonamientos hacia delante y hacia atrás refuerza la teoría de la causación circular.
Por otro lado, Krugman et al.. (2012) explican que algunas regiones cuentan con la ubicación geograficamente apropiada para que la riqueza y la población se concentren. De igual manera, expresan que los efectos de la aglomeración respecto a la dinámica del capital en la ciudad son influyentes para el crecimiento de las ventajas comparativas de la región (Hernández y Carvajal, 2020).
2.4. Teoría de la nueva geografìa económica
El pionero de esta teoría es Paul Krugman con sus trabajos desarrollados en 1991, 1995 y 1999. La nueva geografia económica busca responder un interrogante no explorado en las teorías tradicionales de por qué una empresa o sector específico se localizan en una determinada área geográfica. En esta teoría, el territorio es un elemento esencial del crecimiento económico, pues a través de la innovación y la acumulación de conocimientos, generados por la aglomeración de actividad humana en un territorio, se contribuye al crecimiento y al desarrollo económico (Fujita y Krugman, 2004).
En ese sentido, la concentración de población, producción industrial y de mercados descansan en dos conjuntos de factores. La dotación inicial de los factores de las áreas geográficas y el conjunto de parámetros derivados del comportamiento de los agentes y de la tecnología.
En el primer grupo se encuentran aspectos como el tarmano de población, los recursos naturales, la infraestructura, etc. El segundo grupo hace referencia a parámetros tales como la propensión al consumo de los bienes manufacturados; la intensidad de uso de recursos humanos del sector manufacturero, el grado de economías de escala de las industrias manufactureras; la magnitud de los costos de transporte; el grado de las economías pecuniarias existentes de los sectores industriales, y la magnitud de los eslabonamientos hacia atrás y hacia delante de los sectores industriales (Krugman, 1999; Fujita y Krugman, 2004).
3. Evidencia empírica
En Colombia se han realizado distintos trabajos que involucran el análisis espacial, tanto a nivel regional, departamental y municipal con el objetivo de entender las dinámicas espaciales, y cómo estas impactan en el crecimiento y el desarrollo económico de los territorios.
Sánchez y Núnez (2000) exploraron las relaciones entre las variables geográficas de los municipios de Colombia con el ingreso per cápita y la densidad económica. Los autores concluyen que las variables geográficas afectan el ingreso y el crecimiento de los municipios, ya que dependen de la productividad de la tierra, disponibilidad de recursos naturales, presencia de actividades tropicales y aglomeración de actividades económicas.
En ese orden de ideas, Galvis (2001) en su trabajo sobre la topografia económica de Colombia encontró que la mayor parte de la población y del PIB se concentran en las zonas centrales del país. Igualmente, con el uso de índices de correlación espacial tales como el índice de Moran, Geary, Getis y Ord evaluó la dependencia espacial de la actividad económica de los municipios. Los resultados mostraron altas dependencias en los "antiguos departamentos", pero poca correlación en el resto de los municipios, lo que evidencia la baja integración que existe entre ellos.
De forma similar, Barón-Rivera (2002) identifica las regiones económicas de Colombia con un análisis de clúster, aplicando esa metodología sobre una variable que refleja el desempeno económico de los departamentos a través del tiempo. El autor identificó cinco regiones económicas, en donde las más prósperas son las conformadas por los departamentos a los que pertenecen las 4 principales ciudades colombianas: Bogotá, Medellín, Cali y Barranquilla.
Análogamente, Galvis y Meisel (2010) en un análisis de correlación espacial, utilizan los índices de NBI en los censos de 1973, 1985, 1993 y 2005, encontraron que en Colombia las desigualdades regionales se han mantenido y se han vuelto persistentes, pues al efectuar las correlaciones espaciales entre las condiciones de pobreza de una municipalidad en anos recientes con las de su entorno en épocas posteriores, los autores evidenciaron altas y significativas correlaciones espaciales. Lo anterior lo explican por la existencia de trampas espaciales.
Las metodologías anteriores también han sido aplicadas de formas particulares en el estudio de problemáticas fiscales e impositivas en el país. Por ejemplo, Bonet (2004) presenta evidencia de cómo la descentralización fiscal influye en las disparidades de los ingresos regionales. El autor estimó un modelo econométrico que le permitió medir la desigualdad basada en el concepto de PIB per cápita relativo. De manera similar, estimó el estadístico de Moran y una prueba de multiplicador de Lagrange para distinguir entre modelo de error espacial y modelo de rezago espacial.
En materia de análisis espacial e impuestos, el trabajo realizado por Hernández y Carvajal (2020) estableció medidas que valoran las relaciones del recaudo de impuesto predial per cápita en la actividad económica y los ingresos corrientes per cápita en la eficiencia fiscal del departamento de Boyacá. Para ello, utilizaron una metodología que les permitió detectar la presencia de autocorrelación espacial con el uso del estadístico de Moran y de Geary, además de la inclusión de modelos de econometría espacial. Los autores concluyeron que el impuesto predial per cápita se relaciona negativamente con los niveles de crecimiento económico y resaltaron la importancia del incremento de ingresos corrientes para mejorar la eficiencia fiscal.
De manera igual, en la investigación realizada por Lozano y Ricciulli (2017) acerca de los efectos del impuesto predial en los precios de la vivienda nueva en Bogotá para el período 2009-2016, y mediante el uso de modelos espaciales para datos de panel, encontraron que los aumentos registrados en la tarifa efectiva del predial impactan negativamente los precios de los inmuebles, y que dicho efecto ha venido aumentando en los últimos anos.
4. Metodología
4.1. Fuente de datos
A partir de las operaciones efectivas de caja publicadas por el Departamento Nacional de Planeación (DNP) se obtiene el análisis descriptivo de la situación de la ciudad de Cartagena en su conjunto, en términos de ingresos corrientes, y hace énfasis en el recaudo del impuesto predial de los anos 2000 a 2019. Para el análisis espacial se utilizó, una base estadística del recaudo del impuesto predial por barrios del periodo 2010 a 2019, suministrada por la Secretaría de Hacienda Distrital de la ciudad de Cartagena, cuyos datos fueron indexados para equipararlos a valores de 2019.
4.2. Análisis espacial
Referenciamos la metodología empleada por Galvis y Meisel (2010) justificada por la primera ley de la geografia o ley de Tobler (1970), la cual explica que las interacciones entre los lugares son inversamente proporcionales al coste del recorrido entre ellos, es decir, que en el espacio todos los fenómenos están interrelacionados, pero los más cercanos están más correlacionados que los lejanos.
De acuerdo a lo anterior, en la literatura surgen distintos estadísticos y medidas que permiten estudiar las relaciones espaciales entre diferentes variables, y como explica Celemín (2009), referenciando a Goodchild (1986), el estadístico de Moran es el más utilizado, pues básicamente parte de la definición del coeficiente de correlación de Pearson, pero se le adiciona una matriz de pesos espaciales definida por el usuario.
Una matriz de pesos espaciales (también llamada matriz de contactos o de contigüidad), es una matriz cuadrada, no negativa que especifica el «conjunto de vecindad» para cada observación, en otras palabras, refleja la intensidad de la interdependencia entre un par de regiones en el espacio (Stakhovych y Bijmolt, 2009). Las matrices de pesos espaciales pueden ser de distintos tipos. Siguiendo a Celemín (2009), cuando se tienen en cuenta solo los cuatro elementos que comparten bordes se definen como contigüidad tipo Rook (Torre). Para el caso de que existan ocho vecinos se habla de contigüidad tipo Queen (Reina), y si se toman solamente los vecinos contiguos por el vértice se denomina Bishop (Alfil).
En ese sentido, las formas distintas de contigüidad que siguen las matrices de pesos espaciales son en esencia los movimientos que siguen las fichas del tablero de ajedrez (la Torre, la Reina y el Alfil). La Figura 1, muestra de manera gráfica los tipos de contigüidades de las matrices de contacto.

Fuente: Elaboración propia con en base a Celemín (2009), García-Marí, Sánchez-Vidal y Tomaseti-Solano (2016) y Siabato y Manrique (2019).
Figura 1 Tipos de contigüidad
El tipo de contigüidad usada en este documento para la construcción de la matriz de pesos espaciales es la contigüidad tipo Reina, ya que esta permite establecer una mayor relación de vecindad entre las unidades espaciales estudiadas. Bien, se consideran vecinos tanto los barrios continuos, como los que comparten vértice.
4.2.1. Índice de Moran
El índice, Moran (1950) llamado así en honor al autor que lo desarrolla, es una medida de autocorrelación espacial que permite estudiar variables similares tanto en magnitud como en localización. Aunque la autocorrelación espacial tiene principios similares a las medidas de correlación tradicionales, esta es mucho más compleja, pues permite realizar análisis multidimensionales (en el espacio) y multidireccionales (en el tiempo). Para desarrollar el índice de Moran se siguen las pautas utilizadas en los trabajos de Celemín (2009), Galvis y Meisel (2010) y Siabato y Manrique (2019).
Como se ha explicado anteriormente, la construcción del índice de Moran parte inicialmente de la definición del coeficiente de correlación de Pearson que está definido dadas las variables X y Z como:
Al adicionar una matriz de pesos espaciales Wij para los datos georreferenciados el resultado que se obtiene es el índice de moran:
Donde N es el total de observaciones, el término S0=ΣiΣjWij representa la suma de los elementos espaciales de la matriz. El termino  , y el termino
, y el termino  , hacen referencia a las desviaciones de Xi respecto a su media, donde Xi. es el valor de la variable en una unidad espacial determinada y Xi. es el valor de la variable en otra localización vecina a X. Por último, el término Wij es conocido como el rezago espacial de Z.
, hacen referencia a las desviaciones de Xi respecto a su media, donde Xi. es el valor de la variable en una unidad espacial determinada y Xi. es el valor de la variable en otra localización vecina a X. Por último, el término Wij es conocido como el rezago espacial de Z.
Con el uso de una aproximación de la distribución normal, se puede realizar una inferencia aproximada del estadístico de Moran, asumiendo normalidad y aleatorización de las observaciones, se tiene el siguiente cálculo del estadístico de prueba:
Donde:
La ecuación 4 es conocida como el valor esperado del estadístico I de Moran y la ecuación 5 hace referencia a la varianza de este. El cálculo del estadístico Zi permite conocer si el índice de Moran estimado es estadísticamente significativo. Para ello se establecen las siguientes hipótesis:
H0: No existe autocorrelación espacial
H1: Existe autocorrelación espacial
Por lo tanto, si es significativo, quiere decir que la configuración espacial que se está estudiando no se produce de manera aleatoria y podemos estar en presencia de clustering (si el índice de Moran es positivo) o de un patrón de competencia (si el índice de Moran es negativo).
Otra aproximación para determinar si el índice de Moran es significativo, es el proceso conocido como simulación de Montecarlo, donde se reasignan los valores de Z aleatoriamente en el espacio para generar una distribución de estadísticos I. El valor calculado es, entonces, comparado con el de esa distribución para determinar la significancia estadística (Celemín, 2009; Galvis y Meisel, 2010). En esta investigación se utiliza el proceso de aleatorización anteriormente descrito para conocer la significancia o no del estimador calculado.
4.2.2. Moran's Scatterplot
Una de las herramientas más utilizadas es el diagrama de dispersión de Moran, que permite observar el comportamiento de cada unidad espacial (Anselin, 1995). Como se observa en la Figura 2, el diagrama se puede dividir en cuatro cuadrantes. En el eje de las abscisas, aparecen los valores estandarizados de Z para cada unidad espacial del área estudiada, y en el eje de las ordenadas se encuentran los valores estandarizados del promedio de los valores en unidades vecinas de WZ. Esto se conoce como análisis univariado, puesto que se analiza una variable y cómo influye su vecindario en su comportamiento. De forma similar se pueden realizar análisis bivariados, los cuales permiten comparar dos variables y analizar cómo el contexto de sus vecinos (respecto a una variable) influye en los resultados de otra variable diferente de la unidad de estudio.

Fuente: Elaboración propia con base en Celemín (2009) y Galvis y Meisel (2010).
Figura 2 Diagrama de dispersion de Moran
El cuadrante 1, de la Figura 2 muestra las unidades espaciales con valores encima de la media y que están rodeados de altos valores en su vecindario, situación de alto-alto y también son conocidos como "puntos calientes". La situación contraria se observa en el cuadrante tres y muestra los que están debajo de los valores medios; situación de bajo-bajo, también conocidos como "puntos fríos". El cuadrante II y el cuadrante IV, responden a contextos mixtos. En el primero, se puede identificar una situación de alto-bajo, o sea, las unidades espaciales tienen valores por encima de la media, pero sus vecinos están por debajo de esta. Por último, en el cuadrante IV se encuentran los elementos espaciales, los cuales presentan resultados por debajo del promedio, pero su vecindario tiene resultados por encima de la media de esa variable.
4.2.3. Método LISA
Con el objetivo de determinar la heterogeneidad espacial que posee cada observación espacial, se han desarrollado medidas que permiten capturar indicadores locales de autocorrelación espacial (LISA) y los cuales de forma simultànea dan como resultado la autocorrelación espacial global. Los indicadores locales consideran escenarios específicos, por lo tanto, permiten identificar subzonas en las que se presentan agrupamiento o dispersión del fenómeno (Siabato y Manrique, 2019).
El proceso anterior, permite calcular el índice de Moran local, que ayuda a la identificación de clústeres espaciales y a especificar mejor el análisis espacial realizado. Para el cálculo del índice y la elaboración de los mapas se utilizaron dos programas específicos: ArcGIS desktop y Geoda.
5. Resultados
En esta sección se analizan las estadísticas descriptivas del recaudo del impuesto predial desagregado por barrios en la ciudad de Cartagena, después se calcula el índice de Moran univariado global con su respectivo diagrama de dispersión, posteriormente se calcula el índice de Moran local y se establecen los clústeres espaciales. Al final, se realiza un análisis bivariado con el recaudo en distintos periodos para observar la evolución en el espacio y en tiempo.
5.1. Análisis descriptivo del recaudo del impuesto predial en Cartagena
La Figura 3 muestra la composición del recaudo promedio de los impuestos en el periodo 2000-2019. Como se puede apreciar, para el periodo estudiado, los impuestos más significativos son los de industria y comercio y el predial respectivamente; estos representan el 85% de los ingresos tributarios. En particular, al hablar del impuesto predial, este representa en promedio el 42% del total de los ingresos tributarios. Lo anterior indica la importancia del recaudo del impuesto predial en los ingresos de la ciudad.

Fuente: Elaboción propia con datos del DNP.
Figura 3 Participación promedio de los impuestos en los ingresos tributarios de la ciudad de Cartagena en el periodo 2000-2019
Por su parte, la Figura 4 muestra la evolución del recaudo del impuesto predial en la ciudad de Cartagena. Se observa que en el periodo estudiado el recaudo tiene una tendencia creciente con excepción de los anos donde se han presentado caídas respecto a periodos anteriores, en los anos 2007, 2012, 2016 y 2019.

Fuente: Elaboración propia con datos del DNP Los datos se encuentran en millones de pesos y en precios constantes de 2019.
Figura 4 Evolución del recaudo del impuesto predial en la ciudad de Cartagena en el periodo 2000-2019
Como se observa en la Figura 5, aproximadamente el 88% de los barrios (159 de 179 estudiados) de la ciudad de Cartagena en el periodo de 2010 a 2019, que en promedio pagó valores entre $68.711 y $114.853.422 por concepto del impuesto predial. Por otro lado, aproximadamente el 8% de los barrios pagaron valores entre $114.853.423 y $405.208.511. Solo 5 barrios pagaron en promedio entre $405.208.512 y $1.620.796.216, y solo un barrio pagó el valor máximo por concepto de impuesto predial: la zona industrial de Mamonal. Lo anterior describe una situación en la cual el mayor recaudo del impuesto predial se efectúa en 6 barrios (Mamonal, Bocagrande, Manga, Castillogrande, El Bosque, Centro), los cuales declaran el 57% del total del impuesto predial.
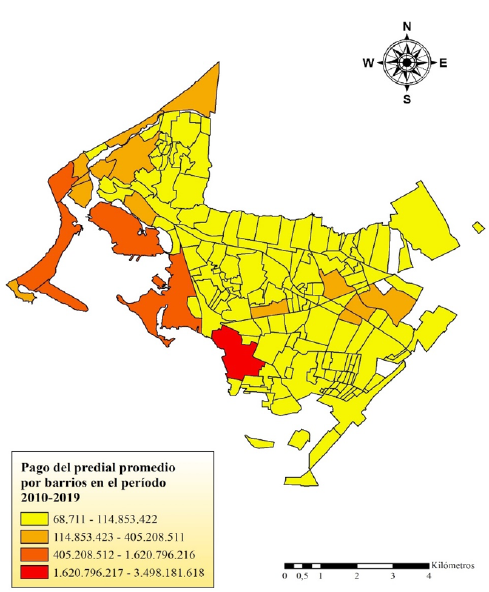
Fuente: Elaboración propia, con el uso de ArcGIS. Los valores se encuentran a precios constantes del 2019.
Figura 5 Mapa recaudo promedio por barrios en la ciudad de Cartagena en el periodo 2010-2019
La situación descrita, se refuerza con la Figura 6, en donde se evidencia la alta diferencia entre la media y la mediana, donde además existe mucha dispersión de los datos y la presencia de datos atípicos (que serían los barrios que más pagan el impuesto predial) es lo que impulsa el valor de la media.
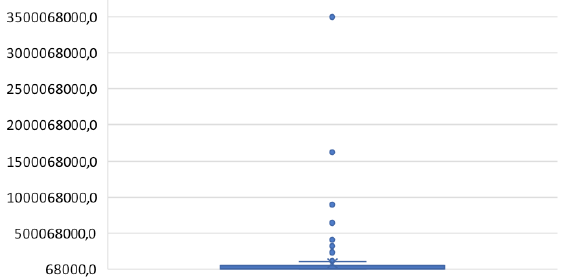
Fuente: Elaboración propia.
Figura 6 Gráfico de cajas y bigotes del pago predial promedio por barrios en el periodo 2010-2019. I
Esto se explica por la forma cómo se recauda el impuesto predial en Cartagena. Los cobros se realizan por el estrato del barrio y el uso del suelo. Por lo tanto, predios de alto valor catastral ubicados en barrios de estratos bajos pueden pagar menos por concepto de impuesto predial. Por otra parte, todos estos barrios concentran mucha actividad comercial, turística, institucional e industrial, por lo que el recaudo del impuesto predial debe focalizarse en esas localidades (y sin perder de vista los altos ingresos de las personas que viven allí).
5.2. Análisis espacial del pago del impuesto predial en la ciudad de Cartagena
En esta sección se realizan los índices de Moran tanto univariado como bivariado para observar si el espacio influye de forma significativa en el recaudo del impuesto predial o si, en su defecto, el territorio no tiene ninguna influencia en el mismo.
5.2.1. Índice de Moran univariado y local univariado
La Figura 7 muestra el valor del índice de Moran univariado y, además, permite observar el diagrama de dispersión de este. Utilizando una matriz de pesos espaciales tipo reina se establecieron los vecinos de cada barrio; precaviéndose, también, que siete barrios están aislados o son considerados "islas", y en consecuencia no se les pudo establecer relaciones de vecindad.
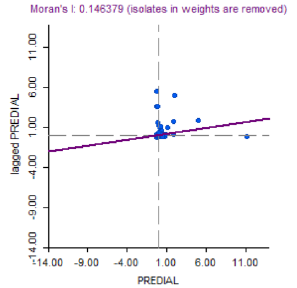
Fuente: Elaboración propia. 7 observaciones son consideradas sin vecinos y han sido removidas.
Figura 7 Diagrama de dispersión de Moran univariado del pago promedio del impuesto predial por barrios en el periodo 2010-2019
Los resultados muestran que el índice de Moran es positivo y tiene un valor de 0.1464, esto quiere decir que existe autocorrelación positiva entre el espacio y el pago del impuesto predial. Para saber si este resultado es significativo, se aplica la prueba de aleatorización y se puede observar en la Figura 8 que el pseudo valor-p es menor que el nivel de confianza del 5%, por lo que se rechaza la hipótesis nula y se puede afirmar que el índice de Moran calculado es estadísticamente significativo.

Fuente: Elaboración propia con la utilización de Geoda.
Figura 8 Prueba de significancia del índice de Moran univariado
Lo anterior implica que el pago del impuesto predial en la ciudad de Cartagena sí está afectado por variables espaciales y cómo la autocorrelación espacial encontrada es positiva, significa que hay aglomeración o clustering espacial. Dicho de otra forma, existen patrones espaciales y relaciones de vecindad que influyen en el pago del impuesto predial de un barrio.
En ese sentido, la Figura 7 también permite dilucidar en qué cuadrante se encuentran los barrios de la ciudad de Cartagena en términos del pago del impuesto predial. Se observa que, en su mayoría, los barrios se encuentran agrupados en el cuadrante III, o la posición de bajo-bajo, lo que implica que la unidad espacial tiene un recaudo bajo y sus vecinos también. De la misma forma, se aprecian unos puntos en el cuadrante 1, es decir, la posición de alto-alto, donde se encuentran los barrios con altos pagos de impuesto predial y sus vecinos también. Para observar de manera más específica este patrón de comportamiento se calcula un índice de Moran local univariado. Así se muestra en la Figura 9.

Fuente: Elaboración propia con la utilización de Geoda.
Figura 9 Mapa de clustering espacial del pago promedio del impuesto predial en el periodo 2010-2019
Como se percibe en la Figura 9, se usa el análisis LISA para calcular los índices locales de Moran, se aprecia que existen 19 barrios en un cluster espacial bajo-bajo; concretamente, son barrios que pagan el impuesto predial por debajo de la media, pero también los barrios que los rodean pagan poco impuesto predial. Por el contrario, existe una aglomeración espacial en el cuadrante alto-alto, en el que se encuentran ubicados 8 barrios de la ciudad de Cartagena; lo que quiere decir que son barrios que pagan el impuesto predial por encima de la media, pero sus vecinos también pagan valores por encima de la media. El detalle de estos barrios se puede ver en la Tabla 1.
En ese orden de ideas, existen 4 barrios que se encuentran en el cuadrante IV en la zona conocida como bajo-alto. Lo que indica que estos barrios pagan valores por debajo de la media del impuesto predial, pero están rodeados por barrios que pagan valores por encima del promedio del impuesto estudiado. La Figura 9, también permite observar que no existe ningun barrio que forme el cluster de la región alto-bajo, dicho de otra manera, los barrios que pagan alto impuesto predial, pero que están rodeados por barrios que pagan menos.
De igual manera, la Figura 10 expone que los clústeres existentes con relación al pago del impuesto predial son significativos. De otro lado, tienen 142 barrios que no son observaciones significativas y 7 barrios sin vecinos, "islas", los cuales no se involucraron en el análisis.
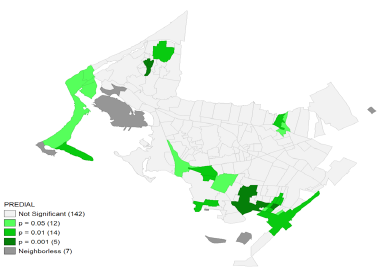
Fuente: Elaboración propia con la utilización de Geoda
Figura 10 Mapa de significancia espacial del pago promedio del impuesto predial en el periodo 2010-2019
La significancia estadística de los resultados anteriores permite comprobar empíricamente la existencia de los "efectos vecindarios" y cómo estos influyen en el pago del impuesto predial unificado en la ciudad de Cartagena.
Son los casos, por ejemplo, de barrios como San isidro y El Campestre, que hacen parte del clúster de "puntos calientes", que están rodeados de barrios de alto recaudo, y a pesar de no pertenecer al intervalo de los barrios que más pagan, como se observa en la Figura 5 (los dos citados se encuentran en el intervalo de recaudo más bajo), al estar rodeados de sectores con alto recaudo como es la zona industrial de Mamonal y el barrio El Bosque, estos impactan de forma positiva en el pago del impuesto predial de los anteriores vecindarios.
El impacto positivo viene determinado como explican Borghi et al., (2010) por un efecto de integración en los mercados, pues las actividades productivas y comerciales que se realizan en un cluster fomentan la innovación, la creación de conocimiento y el desarrollo de un territorio. De manera similar, barrios como Getsemaní, San Diego y La Matuna forman parte de un cluster alto-alto, ya que gracias a las aglomeraciones generadas en la zona norte, en términos de empresas que realizan actividades comerciales, turísticas, financieras e institucionales han ayudado a que mejoren el nivel de ingresos de su población, lo cual repercute en el pago del impuesto predial.
Por otra parte, están los barrios en una situación totalmente inversa a la anterior. Son los que se encuentran ubicados en un cluster de bajo-bajo, en otras palabras, sus vecinos pagan poco impuesto predial y ellos también pagan bajas cantidades de este impuesto. Los resultados muestran que existe una mayor cantidad de aglomeraciones de estos barrios en la ciudad, lo que significa poco recaudo en términos de impuesto predial.
En ese sentido, las aglomeraciones barriales en condición de "puntos fríos" también generan efectos negativos a los vecindarios contiguos. Lo anterior implica, una situación difícil de superar si no se realizan las políticas necesarias para desengranar estos clústeres de pobreza. Un ejemplo de lo anterior se aprecia en el pago de impuesto predial del barrio Daniel Lemaitre, donde existen algunos predios residenciales de alto valor, se encuentra dentro del cluster bajo-bajo y su pago del impuesto predial está por debajo de la media. Dicho caso particularmente permite observar cómo los barrios aledanos que realizan poco pago del impuesto predial afectan de forma negativa el pago del impuesto predial de Daniel Lemaitre.
El último clúster está formado por los barrios que pagan impuesto predial por debajo de la media, pero sus vecinos pagan por encima del promedio del impuesto. Es un clúster especialmente interesante, debido a que se está en presencia de barrios que potencialmente podrían aumentar su pago en términos de impuesto predial, y la situación económica de sus vecinos debería influir positivamente en ellos.
En particular, los barrios que conforman este clúster son Albornoz, Ceballos, Santa Clara y Bellavista. Los dos primeros están registrados como estrato 1, el tercero como estrato 2 y el cuarto como estrato 3. Ellos se encuentran relativamente cerca en términos geográficos de la zona industrial de Mamonal, por lo que deberían presentarse encadenamientos productivos que sirvan como efectos gravitatorios para atraer inversión que genere nuevas empresas y empleos que contribuyan en su desarrollo, lo cual repercutiría de forma positiva en el recaudo del impuesto predial.
No se puede afirmar categóricamente que deban pagar más impuesto predial, pero al estar rodeados de barrios que realizan pagos por encima de la media y de una zona industrial, los citados lugares podrían servir como centros de inversiones de gobiernos locales para impulsar su crecimiento, desarrollo y mejoramiento del nivel de vida de sus habitantes.
5.2.2. Análisis dinámico de la evolución del pago del impuesto predial por barrios en la ciudad de Cartagena
En esta sección se calculan los índices de Moran bivariados, en los que se relaciona el pago del impuesto predial promedio por barrios, de un ano específico con respecto a otro periodo. Luego se realiza el análisis local con la formación de clústeres espaciales para determinar si existieron cambios a través del tiempo en el pago de este impuesto y qué barrios pudieron pasar de un cuadrante a otro.
La Figura 11, permite apreciar los gráficos de dispersión de Moran con su respectivo índice calculado y las pruebas de aleatorización realizadas para evaluar la significancia estadística del índice. Los índices calculados siguen siendo positivos, y, además, son significativos, por lo que se sigue afirmando que existen factores espaciales que influyen en el pago del impuesto predial en la ciudad de Cartagena. Por otro lado, esta figura muestra la mayor limitación del documento, la ausencia de datos en un lapso más grande de tiempo, lo cual permitiría observar los cambios producidos en el recaudo del impuesto predial a través del tiempo con el análisis bivariado de manera mucho más significativa.
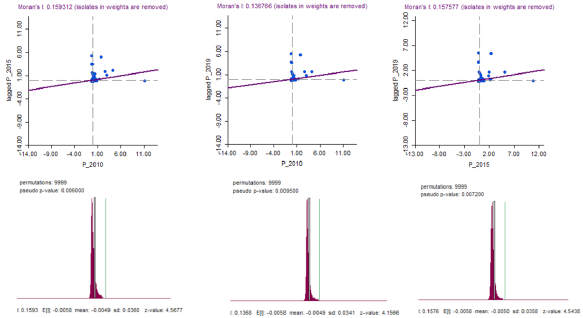
Fuente: elaboración propia con el uso de Geoda. Los datos de pago del impuesto predial están a precios constantes de 2019.
Figura 11 Indice de Moran bivariado del recaudo promedio del impuesto predial por anos 2010-2015, 2010-2019, 2015-2019.
Entre sí las gráficas parecen todas muy similares, no se aprecian cambios importantes en el pago del impuesto predial de los barrios, el comportamiento sigue siendo prácticamente igual al inicialmente calculado. Por lo tanto, se utiliza el análisis local bivariado para ver los clústeres en los que se encuentran los barrios en cada periodo estudiado.
En la Figura 12 se muestra el cálculo del índice de Moran local bivariado, donde al relacionarse distintos periodos de tiempo se observan algunas evoluciones de unos barrios que han pasado de un clúster a otro. Si se centra la atención en la primera columna (de izquierda a derecha) se aprecia el mapa de clustering espacial para el pago del impuesto predial relacionando los anos 2010 y 2015. Se percibe que en ese periodo, había 7 barrios en el cuadrante alto, 19 en el cuadrante bajo-bajo y 5 en el cuadrante de bajo-alto. Se aprecia que el barrio El Campestre se encuentra dentro del cuadrante de bajo-alto.

Fuente: Elaboración propia con el uso de Geoda.
Figura 12 Mapas de clustering espaciales del pago del impuesto predial comparado en los periodos, 2010-2015, 2010-2019, 2015-2019.
Si se examina un periodo más largo de tiempo entre 2010 y 2019 se observa que es muy similar al anterior, de manera que todos los barrios se mantienen en su clúster inicial, a excepción del clúster bajo-bajo, pues se ha anadido un nuevo barrio en esa condición:Villa Rosa. Es decir, al analizar la evolución de los barrios en pago de impuesto predial del periodo anterior, en vez de lograr una mejoría, se produjo un empeoramiento, porque los de más bajo recaudo siguen aglomerándose entre sí.
Al explorar los anos más recientes entre 2015-2019, se observa una evolución en el clúster alto-alto. El barrio El Campestre que se encontraba en el clúster bajo-alto, mejoró en términos de pago del impuesto predial, como consecuencia pasó al clúster alto-alto. En ese sentido se presentó una evolución, pero solo en un barrio.
Al aplicar el análisis dinámico en términos temporales, no se observó evoluciones significativas de los barrios de la ciudad de Cartagena en concepto del pago del impuesto predial, por lo que podemos hablar de un estancamiento, ya que las variables espaciales y las aglomeraciones entre barrios estudiados se mantienen. Los que pagan poco se encuentran rodeados de vecinos que pagan poco y no se ha podido cambiar eso, y los que pagan mucho están rodeados de vecinos que pagan mucho, por lo que las condiciones se han mantenido en el tiempo en un equilibrio negativo.
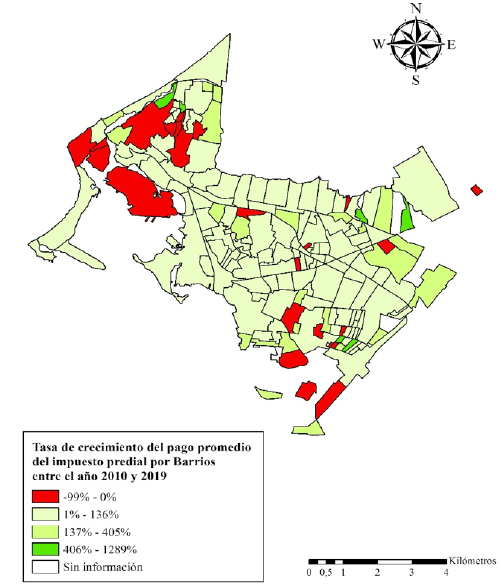
La Figura 13 muestra el cambio porcentual del recaudo promedio del impuesto predial, por vecindarios en los anos 2010 y 2019. Se observa que aproximadamente el 14% de los barrios, presentó decrecimiento por concepto del pago del impuesto predial unificado. Entre estos, se encuentran algunos de estratos altos como el Centro, La Matuna, Getsemaní y Manga, que han disminuido su pago del impuesto predial en los periodos estudiados. Desde otra perspectiva, el resto de los barrios de la ciudad de Cartagena incrementaron su pago de este impuesto. Aunque las tasas de crecimiento de algunos barrios son altas, su impacto en el recaudo general es poco significativo, por lo que son barrios de estratos bajos que pagaban muy poco. Por otro lado, es importante recalcar que existen factores adicionales que impactan en el recaudo del impuesto predial y que no han sido considerados en esta investigación, entre otros, la cultura tributaria, el nivel de ingreso de las familias, los avalúos catastrales de los predios, el tipo impositivo medio.
6. Discusión de resultados
Los resultados arrojaron que existe influencia de patrones espaciales en el pago del impuesto predial, o sea, las variables espaciales no se comportan de forma aleatoria, sino que afectan el pago del impuesto estudiado. Al presentar correlación positiva entre la ubicación del barrio y el pago del impuesto predial, el índice de Moran indica que se está en presencia de aglomeraciones o clustering espaciales.
En ese sentido, al calcular el índice de Moran local, se encontró que la mayoría de los barrios hacen parte del clúster de los "puntos fríos", por ende, hay barrios que pagan bajos valores en promedio del impuesto predial y que están rodeados por vecinos que pagan bajo impuesto predial. El efecto vecindario de los barrios aledanos influye negativamente en el pago del impuesto predial, por consiguiente, el circuito de pobreza en el que se hallan no ayuda a la recaudación de este.
Por el contrario, existe un pequeno porcentaje de barrios integrantes del clúster de los "puntos calientes", barrios que pagan alto impuesto predial, y que sus vecinos pagan también altos valores del impuesto. Estos, por su parte, sufren de un efecto vecindario positivo por las dinámicas empresariales, comerciales, institucionales y turísticas que se manejan en ellos, y, por supuesto, repercuten en el mejoramiento de los vecinos.
De mismo modo, existe otro clúster conformado por barrios que pagan impuesto predial por debajo de la media, pero están rodeados por barrios que pagan el impuesto predial por encima de la media. Ellos merecen especial atención, de manera que podrían potencialmente aumentar su nivel de pagos, debido a que son geográficamente cercanos a la zona industrial de Mamonal, por lo que teóricamente deberían recibir un efecto vecindario positivo que ayude a impulsarlos, lo cual repercutiría directamente en el pago de los impuestos.
Respecto al análisis dinámico, al calcular el índice de Moran bivariado, utilizando el pago del impuesto predial promedio por barrios, en distintos periodos, se pudo observar que no hubo variaciones espaciales significativas, en otras palabras, que solo dos barrios pasaron de un clúster espacial a otro, por lo tanto, en los 10 anos analizados, el comportamiento de los barrios con relación al pago del impuesto predial se mantuvo estable, lo cual implica la presencia de un desequilibrio insano; de tal forma, los clústeres de los puntos calientes se han mantenido, y asimismo, los de los puntos fríos, y no se ve una evolución en otros barrios en aras de pasar de un peor estado a uno mejor.
Al observar las variaciones porcentuales del periodo inicial (2010) con respecto al periodo final (2019), se aprecia que muchos barrios aumentaron su pago del impuesto predial, con tasas, incluso, por encima del 100%, pero al contextualizar esos valores se observa que muchos barrios han estado pagando poco o nada por concepto de este impuesto, inclusive, barrios de alta estratificación han disminuido sus pagos. Por lo tanto, estos cambios, aunque positivos para el recaudo no son suficientes y se deberían mejorar las condiciones de vida y procurar por un crecimiento óptimo de las comunidades de la ciudad para que el pago de impuestos aumente.
Por otro lado, los resultados son consistentes con los obtenidos por Sánchez y Núnez (2000), Galvis (2001), Galvis y Meisel (2010), Lozano y Ricciulli (2017) y Hernández y Carvajal (2020) pues, al explorar la relación existente entre variables geográficas y económicas se observa que en muchas ocasiones estas interacciones son significativas y se encuentran espacialmente correlacionadas, lo que, a su vez, determina el cumplimiento empírico de la ley de Tobler, puesto que los eventos que suceden en el espacio están más interrelacionados si menor es la distancia entre ellos.
7. Conclusiones
El impuesto predial unificado representa más del 40% de los ingresos tributarios de la ciudad de Cartagena, por consiguiente, es importante buscar estrategias que permitan incrementar su recaudación, tal propósito debe ser fundamental los para tomadores de decisiones. Por eso, esta investigación, a través de métodos de econometría espacial buscó establecer la relación entre el espacio y el pago del impuesto predial por barrios en la ciudad de Cartagena.
El análisis espacial mostró que la ubicación del barrio tiene una influencia directa en el pago del impuesto predial unificado del mismo. Dicho de otra manera, las variables espaciales afectan el pago del este impuesto. Asimismo, se halló que la mayoría de los barrios se encuentran agrupados en el clúster de los puntos fríos. De forma análoga, hay unos barrios ubicados en el clúster de los puntos calientes. Esto comprueba la existencia de efectos vecindarios tanto positivos como negativos.
Esta situación refleja el nivel de desigualdad que existe en la ciudad de Cartagena, dado que la generación de riqueza, empleo y valor agregado se encuentran agrupadas en zonas específicas de la ciudad. Por ello, es importante realizar análisis más desagregados para entender mejor las dinámicas de cada territorio. En ese sentido hubo limitaciones para conseguir datos desagrupados por barrios de variables de pobreza, desigualdad, ingreso, entre otras. Por otra parte, no se pudo obtener una base de datos más longeva para realizar de mejor forma el análisis dinámico y observar qué cambios se han dado a lo largo del tiempo. Esto abre posibilidades a nuevas investigaciones dentro de este ámbito que ayuden a la toma de decisiones en política económica.
Los resultados obtenidos dejan claridad sobre dos aspectos importantes. Primero, que la ciudad debe en lo posible cambiar la forma de cómo recauda el impuesto predial unificado, es decir, urge implementar un sistema de cobro similar al de ciudades como Bogotá, Medellín, Barranquilla, etc. En el que se cobre de acuerdo al estrato del barrio, el uso del terreno, pero también a la valorización del predio. Segundo, es importante realizar proyectos de inversión pública que ayuden al mejoramiento de los barrios, que impacte en la creación de empresas, empleos, educación, en la disminución de la delincuencia, y, lo más importante, en el mejoramiento en la calidad de vida de sus habitantes.
En ese sentido, este documento provee información referente a barrios que serían entidades espaciales importantes con las que empezar a trabajar, puesto que, los efectos vecindarios positivos que se generen tendrían un impacto mucho mayor, lo cual contribuiría a la rápida expansión, crecimiento y desarrollo de dichos barrios, que, finalmente, como se ha explicado, influiría directamente en el cobro de impuestos y en la mejora de los ingresos tributarios de la ciudad.