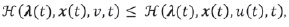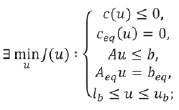Control óptimo conmutado de un convertidor CC-CC¹

Switched optimal control of a DC-DC converter

Controle ótimo comutado de um conversor CC-CC

D. E. Méndez, J. Sánchez^* y R. Alzate^**

¹ Producto derivado del proyecto de grado en la modalidad de investigación "Análisis de optimalidad para un control conmutado aplicado en un convertidor de potencia" presentado para optar al título de Ingeniero Electrónico. Trabajo adscrito al Grupo de Investigación CEMOS, de la Universidad Industrial de Santander (UIS) en Bucaramanga - Colombia.
^* D.E. Méndez (diego.esteban@correo.uis.edu.co) y J. Sánchez-Carvajalino (jaffraith.sanchez@correo.uis.edu.co) son Ingenieros Electrónicos egresados de la Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones (E3T) de la Universidad Industrial de Santander (UIS) en Bucaramanga - Colombia.
^** R. Alzate es Profesor Asistente, de Tiempo Completo, en la Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones (E3T) de la Universidad Industrial de Santander (UIS), en Bucaramanga - Colombia; e-mail: ralzatec@uis.edu.co

Recibido Agosto 17 de 2015 - Aceptado Febrero 19 de 2016

Resumen

El presente artículo aborda el control de circuitos convertidores de potencia empleando control óptimo conmutado. Se realiza el diseño y la simulación para un convertidor CC-CC tipo reductor (Buck) y posteriormente se ajusta para el mismo un lazo realimentado en el cual se verifica el efecto de una acción de tipo proporcional de alta ganancia (encendido-apagado) a manera de punto de referencia convencional, para atenuar la incidencia de perturbaciones aplicadas en el sistema. Posteriormente y empleando un enfoque basado en el principio del máximo de Pontryagin, se diseña e implementa, a través de simulación, una técnica de control óptimo conmutado (bang-bang) que permite obtener un desempeño comparable con la acción encendido-apagado en términos de características dinámicas. Pruebas adicionales permiten cuantificar la optimalidad de la técnica propuesta y verificar el desempeño del sistema controlado en términos energéticos, mostrando que un control óptimo conmutado presenta además de la minimización del funcional de costo (mínima energía del error), una menor incidencia en la generación de ruidos por conmutación de alta frecuencia, en comparación con la técnica convencional. Trabajo adicional incluye la verificación experimental en laboratorio para los resultados de simulación presentados.

Palabras clave: Control bang-bang, control óptimo conmutado, convertidor de potencia Buck, principio del máximo de Pontryagin.

Abstract

In this work, switching-based control is applied on regulation of power conversion circuits. In particular, a DC-DC Buck-type power converter has been designed and simulated, both for nominal conditions and under disturbances. First of all, a classical On-Off controller was employed to compensate the effects of disturbances in the loop, in order to check the correctness of the operational conditions for the controlled system. Then, an optimal-switching bang-bang controlled was designed and implemented, taking into account the Pontryagin's Maximum principle, showing a good performance for disturbance rejection, improvement of dynamical features in the response and reduction of error's energy by mean of verification of optimality criteria. Results show that despite the fact both techniques analyzed; i.e. On-Off and bang-bang, are switching-based laws, the performance index on the optimal controller allows to obtain a cleaner shape with less energy consumption. Ongoing work includes the experimental verification of the optimal technique in laboratory.

Key words: Bang-bang control, switching-optimal control Buck power conversion circuit, Pontryagin's maximum principle.

Resumo

Este artigo descreve os conversores de energia de controle circuito empregando optivo de controle. Se realiza o projeto e a estimulação para um convertedor CC-CC tipo redutor (buck) e posteriormente se ajusta para o mesmo um laço realimentado no qual se verifica o efeito de uma ação de tipo proporcional de alto ganho (ligado-desligado) o título de referência convencional reduzir a incidência de distúrbios aplicado sistema. Posteriormente e usando um foco baseado no principio do máximo de Pontryagin, se projeta e implementa, através de simulação, uma técnica de ótimo controle comutado (bang-bang) que permite obter um desempenho comparável com a ação ligado-desligado em términos de características dinâmicas. Testes adicionais permitem que o Optimalidade da proposta técnica para quantificar e verificar o desempenho do sistema de energia controlada, mostrando que um ótimo controle apresenta além da minimização do funcional de custo (potência mínima do erro), uma menor incidência na geração de ruídos por comutação de alta frequência, em comparação com a técnica convencional. Trabalho adicional inclui a verificação experimental em laboratório para os resultados de simulação apresentados.

Palavras chave: Controle Bang-Bang, ótimo controle comutado, Buck, o conversor de energia de princípio do máximo de Pontryagin.

I. Introducción

EL consumo energético mundial se ha incrementado en las últimas décadas como consecuencia de un acelerado crecimiento en la demanda de recursos, lo que genera fuertes impactos ambientales relacionados principalmente con emisiones contaminantes por uso de combustibles fósiles y otras fuentes de energía no renovable. En la búsqueda por reducir estas consecuencias indeseadas, se propende por mejorar el desempeño de los sistemas de gestión de energía, procurando el mayor aprovechamiento con menores pérdidas [1].

En el caso particular de los sistemas eléctricos, el gestor de energía se constituye a través de los denominados circuitos convertidores de potencia, cuya función es suministrar a una carga eléctrica los niveles de tensión y voltaje adecuados, transferidos desde una fuente de suministro, mediante la acción controlada de dispositivos de conmutación [2]. Este control se realiza en la mayoría de casos a través de la selección adecuada del patrón de una señal de gobierno modulada en ancho de pulso (PWM, pulse width modulated), mediante técnicas de control clásico en el dominio de la frecuencia o moderno en el espacio de estados [3]-[7]. Sin embargo, si se desea maximizar un índice de desempeño (como bien puede ser la reducción de pérdidas energéticas), el control óptimo es la mejor opción [8][9][10].

Una de las técnicas de control óptimo más sencillas es el controlador de tiempo mínimo o control bang-bang, el cual es un claro ejemplo de control conmutado, debido al carácter discontinuo para la ley de control resultante [11]. Dicha técnica puede considerarse como una versión mejorada del control encendido-apagado (on-off), desde el punto de vista energético, dando pie al desarrollo de un nuevo conjunto de técnicas denominadas de control "híbrido" [12][13][14], que buscan aprovechar las discontinuidades de campos vectoriales, para realizar manipulaciones apropiadas del comportamiento dinámico de sistemas complejos.

La solución de un problema de control óptimo es en general una tarea poco trivial, pues se deben asegurar condiciones de existencia y unicidad, además de estabilidad, para la solución óptima [15]. El problema se complica aún más cuando la descripción del sistema es condicionada como en los sistemas híbridos. Al respecto se reportan resultados en la literatura que buscan definir las condiciones para resolver problemas de control óptimo en sistemas conmutados [16] [17][18][19][20]. En cualquiera de ellos, el reto está en formular adecuadamente la secuencia de conmutación que minimiza el funcional de costo, garantizando la convergencia de la solución. En este contexto el controlador bang-bang sólo requiere una conmutación por periodo, facilitando su resolución mediante aproximaciones numéricas (i.e. programación dinámica).

La mayor contribución del presente artículo es por tanto, la aplicación del control bang-bang como control óptimo conmutado para regular el comportamiento de un circuito convertidor de potencia. Para ello se abordan los siguientes contenidos: la sección II describe los fundamentos del control óptimo y el control bang-bang; la sección III presenta los resultados de simulación comparativos para el control bang-bang y un control conmutado convencional de tipo encendido-apagado aplicados en un convertidor CC-CC reductor. Finalmente, se presenta en la sección IV la conclusión general del trabajo.

II. Metodología y Materiales

El problema de control óptimo puede resumirse en resolver la optimalidad de un funcional J que depende de un cierto conjunto de funciones u(t) correspondientes con el esfuerzo de una acción de control [15]. En otras palabras, siendo un sistema dinámico descrito por la ecuación de estados:

donde x representa los estados del sistema y u es el vector de entradas o forzantes, es posible plantear un problema de optimización (con o sin restricciones) consistente en minimizar o maximizar el siguiente funcional de costo o índice de desempeño:

donde ψ(.) es una condición terminal sobre el estado y L se denomina el lagrangiano del sistema.

Para garantizar la optimalidad de (2); es decir, para garantizar la existencia de una solución para el problema de control óptimo, se deben satisfacer las condiciones del denominado principio del máximo de Pontryagin, enunciado en el modo siguiente [15]:

Teorema (Principio del Máximo)

Suponga que Suponga que u(t) y x(t) representan y representan respectivamente el control óptimo y la trayectoria de estado para un problema de control óptimo. Entonces, existe una trayectoria adjunta λ(t)tal que, junto con u(t), x(t) y λ(t) y satisfacen:

para todo 0 ≤ t ≤ T, y todo v € U, tal que:

donde H es el hamiltoniano dado por:

A. Control conmutado de mínimo tiempo (bang-bang)

Como caso de aplicación para el principio del máximo, se presenta el problema de control del tiempo mínimo, en el cual se propone un problema de optimización con restricciones, donde:

sometido a -1 ≤ u(t) ≤ 1 y condiciones finales deseadas nulas para el vector de estados (i.e. ψ(x(tf) = 0), partiendo de condiciones iniciales arbitrarias. De esta manera, es evidente la forma que toma el lagrangiano del sistema:

a partir del cual es posible formular el hamiltoniano correspondiente:

que para el caso de un sistema lineal:

resulta, por el principio del máximo, en una solución óptima del tipo [21]:

donde sign(.) es la función signo y λ(t) la solución de la ecuación adjunta correspondiente.

B. Control bang-bang de un convertidor Buck

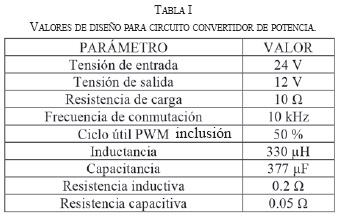
La Fig. 1, ilustra el diagrama esquemático de un circuito convertidor de potencia CC-CC tipo reductor (Buck). Dicho circuito fue diseñado para satisfacer las características nominales incluidas en los parámetros de la Tabla 1.

El modelo del circuito en el espacio de estados, puede escribirse como:

siendo

para x₁(t) representando la corriente en el inductor, x₂(t) la tensión en el capacitor y u(t) el valor de ciclo útil de la señal de conmutación modulada en ancho de pulso.

Ahora bien, resolver el problema de control de tiempo mínimo para este sistema es equivalente a reducir a cero el error del vector de estado, con respecto a valores de estado estacionario deseados. De esta manera, puede formularse el siguiente funcional de costo:

para regular la tensión de salida en el convertidor (siendo x_2d = 12V ), con restricciones sobre la señal de control dadas por:

considerando un ciclo útil porcentual. Luego, dada la dificultad para resolver analíticamente la ecuación adjunta correspondiente, se procede a aproximar una solución numérica para la señal de control óptimo empleando el paquete de herramientas de optimización de MATLAB®. En particular, se configuró un problema de optimización no lineal con restricciones a partir de la función fnincon(.) tomando como base la descomposición en intervalos sugerida en [22]. Para ilustración, el procedimiento numérico ejecutado se describe en el Apéndice al final del artículo.

III. Resultados y discusión

Inicialmente, la Fig. 2 muestra la simulación en MATLAB® para la tensión de salida del circuito en lazo abierto sin control, cuando se aplica una perturbación en la entrada de suministro V_m in correspondiente con un decremento del 25 % en su valor nominal, pasando de 24 V a 18 V en t = 25 ms. Como se observa, posterior a la perturbación el sistema no mantiene la tensión nominal deseada a la salida, cayendo a 8.8 V. Este comportamiento justifica la inclusión de un controlador que permita regular los niveles de tensión de salida hacia valores nominales deseados, a pesar de la influencia de perturbaciones.

La primera estrategia de control verificada corresponde a un control proporcional de alta ganancia (control encendido-apagado), con resultados para la tensión de salida regulada y señal de control, ilustrados respectivamente en las Figs. 3 y 4.

A partir de ello, se experimenta una notable disminución en el efecto de la perturbación, debido al incremento de energía en la señal de control. Sin embargo, también se denota mayor presencia de micro-oscilaciones en la respuesta (chattering), apreciados de manera más visible en la señal de control, la cual conmuta alrededor de sus valores extremos (constituyendo por tanto una acción de control conmutado).

Posteriormente, se presentan en las Figs. 5 y 6 resultados equivalentes para el caso del control óptimo conmutado de tipo bang-bang.

Para este caso, se eliminan las micro-oscilaciones (chattering) de la respuesta del sistema y se reduce de manera notoria el sobreimpulso inicial, aunque también se presenta un transitorio levemente más prolongado, incluso al momento de aplicarse la perturbación en la carga. En términos de la señal de control, se observa cómo el valor del ciclo útil tiende a establecerse alrededor del valor nominal (50 %) antes de aplicarse la perturbación en t = 0.025 s, momento en el cual se posiciona en un valor mayor para efectos de compensación. Desde el punto de vista del desgaste de elementos de actuación y generación de ruidos de alta frecuencia, este comportamiento es deseable en comparación con el tipo de señal del controlador encendido-apagado.

Adicionalmente, la Fig. 7 permite comparar el desempeño para ambas estrategias de control desde el punto de vista energético, donde se comprueba cómo a partir del cálculo del funcional de costo considerado en (5), la energía del error se minimiza para la estrategia óptima y por tanto, se puede verificar que una estrategia de control se puede valorar, no solamente desde el punto de vista del valor de las variables de interés en estado estacionario, sino también a partir del cómo puede obtenerse el objetivo de control empleando un menor esfuerzo (o equivalentemente con una mínima energía).

IV. Conclusiones

El control conmutado se incluye dentro del conjunto de técnicas de control híbrido que combinan descripciones continuas con transiciones (discontinuidades) generalmente de tipo discreto. Un control proporcional de alta ganancia (en su forma de control encendido-apagado) puede verse como una forma de control conmutado debido al carácter discontinuo de la señal resultante. El efecto de este tipo de control es una mayor fuerza aplicada en el actuador, lo cual eventualmente puede presentar micro-oscilaciones de alta frecuencia (chattering) con efectos nocivos correspondientes. El control bang-bang es una clase particular de control conmutado que puede derivarse mediante el problema de optimización del mínimo tiempo. El presente artículo permitió mostrar cómo una estrategia de control bang-bang, partiendo del mismo principio de conmutar entre dos valores admisibles, concentra en un modo más eficiente la energía de la señal de control, haciendo que se obtenga el resultado deseado a la salida con un menor consumo reflejado en la minimización del funcional de costo. Se empleó como ejemplo el problema de regular la tensión de salida en un circuito convertidor de potencia ante la acción de perturbaciones en su entrada. Trabajos adicionales implican la verificación experimental en laboratorio para los resultados presentados y la exploración de aplicaciones a mayor escala de potencia.

Apéndice: Solución numérica del problema de optimización

La función fmincon (.) de MATLAB® forma parte del paquete de herramientas de optimización (Optimization toolbox [23]). Dicha función, resuelve un problema formulado de la siguiente manera:

siendo J(u) la función objetivo a minimizar, u el parámetro de optimalidad, c(u) las restricciones no lineales de desigualdad, c_eq(u) las restricciones no lineales de igualdad, {A, A_eq, b, b_eq} los parámetros para las restricciones lineales de igualdad y desigualdad, mientras que {l_b, u_b} son respectivamente las cotas inferior y superior para u .

Por ser un problema de optimización para hallar el tiempo mínimo, se plantea J(u)=t. Ahora bien, numéricamente la información para este funcional en términos del vector de estados del sistema implica adicionar una tercera variable dinámica x₃(t) = t, para forzar a que la minimización de J(u) corresponda con la minimización de esta tercera variable de estado. Así entonces, el nuevo vector de estados se representa mediante:

con lo cual, la dinámica del sistema ampliado se convierte en:

Luego, tomando en consideración las características del problema, se incorpora la condición final deseada (estado final en condición de reposo) a manera de restricción de igualdad no lineal; es decir:

Nótese cómo la restricción en el valor final se realiza sobre el vector de estados original x, y no en su versión ampliada z, debido a que en este último la dirección adicional corresponde con el funcional de costo a optimizar. Asimismo, para este problema particular, no se emplean (y por tanto no se definen) funciones de restricción no lineal de desigualdad c(u), ni restricciones lineales dadas por {A, A_eq, b, b_eq}. Sin embargo, es requerido que l_b = -1 y u_b = 1; es decir: -1 ≤ u ≤ 1

De esta manera, el diagrama de flujo de señal ilustrado en la Fig. 8 presenta el desarrollo lógico del algoritmo que permite encontrar el valor de la señal de control u que minimiza el índice de desempeño J(u) .

Referencias

[1] I. E. Agency, "Key world energy statistics 2014," 2014.         [ Links ]

[2] D. W. Hart, Electrónica de Potencia. Pearson Educación, SA, 2001.         [ Links ]

[3] J. G. Kassakian, M. F. Schlecht, and G. C. Verghese, Principles of power electronics. Addison-Wesley Reading, USA, 1991.         [ Links ]

[4] R.W. Erickson and D. Maksimovic, Fundamentals of power electronics. Springer, 2001.         [ Links ]

[5] V. Utkin, J. Guldner, and M. Shijun, Sliding mode control in electromechanical systems. CRC press, 1999, vol. 34.         [ Links ]

[6] H. Sira-Ramírez and R. Silva-Ortigoza, Control design techniques in power electronics devices. Springer, 2006.         [ Links ]

[7] C. Elmas, O. Deperlioglu, and H. H. Sayan, "Adaptive fuzzy logic controller for dc-dc converters," Expert Systems with Applications, vol. 36, no. 2, pp. 1540-1548, 2009.         [ Links ]

[8] R. Sepulchre, M. Jankovic, and P. V. Kokotovic, Constructive nonlinear control. Springer-Verlag, Berlin., 1997.         [ Links ]

[9] M. Pahlevaninezhad, P. Das, J. Drobnik, G. Moschopoulos, P. K. Jain, and A. Bakhshai, "A nonlinear optimal control approach based on the control-lyapunov function for an ac/dc converter used in electric vehicles," Industrial Informatics, IEEE Transactions on, vol. 8, no. 3, pp. 596-614, 2012.         [ Links ]

[10] X. Liu, G. Zhang, D. Yang, T. Shi, and X. He, "Discrete-time optimal control of photovoltaic grid-connected inverter based on particle swarm optimization," Mathematical Problems in Engineering, 2014.         [ Links ]

[11] di Bernardo, M., Budd, C., Champneys, A.R., and Kowalczyk, P. Piecewise-smooth dynamical systems: theory and applications. London: Springer-Verlag, 2008.         [ Links ]

[12] Goebel, R., Sanfelice, R. G. and Teel, A. R. Hybrid dynamical systems. IEEE Control Systems Magazine, vol.29 (2), pp. 28-93, 2009.         [ Links ]

[13] Rubaai, A. and Jerry, J. Hybrid fuzzy bang-bang mode controller with switching function for electric motor drives applications. Industry Applications IEEE Transactions on, vol. 50 (3), pp. 2269-2276, 2014.         [ Links ]

[14] N. Aghasadeghi, A. Long, and T. Bretl, "Inverse optimal control for a hybrid dynamical system with impacts," in Robotics and Automation (ICRA), 2012 IEEE International Conference on. IEEE, 2012, pp. 4962-4967.         [ Links ]

[15] R.W.H. Sargent, Optimal control, Journal of Computational and Applied Mathematics, Volume 124, Issues 1-2, pp. 361-371. 2000.         [ Links ]

[16] Xuping Xu; Antsaklis, P.J., "Optimal control of switched systems based on parameterization of the switching instants," in Automatic Control, IEEE Transactions on, vol.49, no.1, pp.2-16, Jan. 2004.         [ Links ]

[17] Shahid Shaikh, M.; Caines, P.E., "On the Hybrid Optimal Control Problem: Theory and Algorithms," in Automatic Control, IEEE Transactions on, vol.52, no.9, pp.1587-1603, Sept. 2007.         [ Links ]

[18] Jian Xu; Qijun Chen, "Optimal control of switched hybrid systems," in Control Conference (ASCC), 2011 8th Asian, vol., no., pp.1216-1220, 15-18 May 2011.         [ Links ]

[19] Sorin C. Bengea, Raymond A. DeCarlo, Optimal control of switching systems, Automatica, Volume 41, Issue 1, January 2005, Pages 11-27.         [ Links ]

[20] Ghomanjani, F.; Farahi, M. H., "Optimal Control of Switched Systems based on Bezier Control Points," in I. J. Intelligent Systems and Applications, vol.4, no.7, pp.16-22, Jun. 2012.         [ Links ]

[21] Lucas, S.K.; Kaya, C.Y., "Switching-time computation for bang-bang control laws," American Control Conference, 2001. Proceedings of the 2001, vol.1, no., pp.176,181 vol.1, 2001.         [ Links ]

[22] X. Wang. Solving optimal control problems with MATLAB: Indirect methods. Technical report, ISE Dept., NCSU, 2009.         [ Links ]

[23] Optimization Toolbox™ User's Guide, The MathWorks, Inc., 2015.         [ Links ]

Diego Alfonso Esteban Méndez. Nació en Bucaramanga, Colombia, el 23 de marzo de 1990. Culminó sus estudios de Ingeniería Electrónica en la Universidad Industrial de Santander en 2015. Sus intereses de investigación se orientan hacia el análisis de optimalidad en sistemas de gestión de energía.

Jaffraith Sánchez Carvajalino. Nació en Ocaña, Colombia, el 16 de marzo de 1988. Culminó sus estudios de Ingeniería Electrónica en la Universidad Industrial de Santander en 2015. Sus intereses de investigación se orientan hacia el desarrollo de algoritmos para el cálculo variacional de la dinámica de sistemas eléctricos.

Ricardo Alzate Castaño (M'09). Nació en Palmira, Colombia, el 06 de marzo de 1979. Obtuvo el Título de Ingeniero Electrónico en 2003, y de Magister en Automatización Industrial en 2006, ambos otorgados por la Universidad Nacional de Colombia - Sede Manizales. En 2009 obtuvo el título de Doctor en Automatización por parte de la Universidad de Nápoles FEDERICO II en Italia. Desde 2010 está vinculado como Profesor de Tiempo Completo en la Escuela de Ingenierías Eléctrica Electrónica y de Telecomunicaciones (E3T) de la Universidad Industrial de Santander (UIS), en Bucaramanga - Colombia. Sus intereses de investigación incluyen el análisis de sistemas dinámicos no lineales y la síntesis de estrategias avanzadas de control para sistemas de gestión de energía.