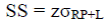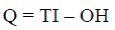I. Introducción

DE acuerdo a la Red Sismológica Nacional de Colombia, en el Distrito de Barrancabermeja, se encuentra ubicada en una de las zonas de mayor actividad sísmica del país en el llamado “nido sísmico” de Bucaramanga. En Colombia según análisis de la Red sismológica de Colombia, se presentaron en el 2016 cerca de once mil movimientos telúricos de los cuales el 50% de estos movimientos se presentaron en Santander.

La comunidad científica, en la búsqueda de mitigar el impacto en los niveles de inventarios que podrían presentarse después de un desastre. Han creado modelos y políticas como transbordo lateral y revisión periódica de inventarios, lo cual permite administrar la gestión de inventarios involucrando almacenamiento, transporte y funciones de distribución. Las personas afectadas por desastres naturales dependen de la asistencia de organizaciones humanitarias que gestionan alimentos, refugios, agua y elementos de primera necesidad, es así como los productos se distribuyen a los albergues en una gran región geográfica dependiendo del tipo y la intensidad del desastre, a menudo es práctico tener varios albergues paralelos que brinden el servicio de ayuda humanitaria a población más afectada. Estos albergues normalmente reponen sus existencias desde un centro de distribución. En el caso de un tiempo de falta de existencias en un albergue, el reabastecimiento se hará desde un albergue cercano, teniendo respuestas esenciales en el rendimiento del servicio del sistema. Dichos envíos entre albergues se denominan transbordos laterales (de emergencia). Este documento proporciona un enfoque para modelar sistemas con transbordos laterales en caso de políticas de pedidos uno por uno y demanda estocástica.

Por tal motivo, este artículo desarrolla un modelo basado en la gestión de inventarios para la distribución de ayudas humanitarias en los diferentes puntos de albergues designados para la atención de personas afectadas, por un posible desastre natural, con el objetivo de visualizar la distribución de ayudas humanitarias y el efecto del transbordo lateral en un albergue.

Existen distintos métodos para la selección de políticas de gestión de inventarios en logística humanitaria, con distintos enfoques como lo es el modelo de envío directo, modelo con transbordo lateral y el modelo de transbordo lateral marítimo, enfocado a las oportunidades de transbordo lateral en la cadena de ayudas humanitarias, proponiendo un sistema de distribución con dos escalones para un posible escenario de terremoto donde se tiene en el escalón superior las instalaciones de socorro y los lugares de demanda en el escalón inferior. Teniendo como prioridad el transbordo lateral entre las instalaciones de socorro [¹]. También, se encuentra un modelo de inventarios de relevo con tiempos de entrega y demanda estocástica, en el cual se prioriza la demanda irregular y la interrupción de la red de comunicaciones, siendo características de situaciones que exige la logística humanitaria, desarrollando un modelo de inventario de socorro humanitario en casos de desastres que sume una función distribuida uniformemente en los parámetros de tiempo de entrega y demanda, como la distribución normal y de poisson.[²]. Así mismo, un modelo de inventario de ayudas en caso de desastres basado en transbordo. Utilizando simulación de dinámica de sistemas para comparar el control de inventario y los costos en una cada de suministro humanitario sin transbordo frente a una con transbordo [³].

La programación logística de emergencia en desastres naturales implica el envío de productos a los centros de distribución en áreas de desastre lo antes posible y así acelerar la operación de socorro. Integrando tres modelos de planificación en un sistema de apoyo a las decisiones de logística humanitaria, teniendo en cuenta bases de datos relevantes como (unidades de almacenamiento, centro de distribución de ayudas, redes nacionales de transporte, equipos de búsqueda y rescate) [⁴].

La planificación y gestión de inventarios de ayuda humanitaria en casos de desastres incluye un sistema de suministro y logística. Basado en un modelo de inventario de revisión de orden fija con un patrón de distribución desconocida, en el que se permite transbordo lateral entre dos puntos de refugio, clasificando el nivel de existencias en tres categorías, alto, medio y bajo. En caso de escasez en algún lugar, otro proporcionará cierta cantidad de sus existencias con una probabilidad de ayuda [⁵]. Ahora bien, los sistemas de inventario con varias bases que soportan diferentes regiones geográficas, es bastante común permitir transbordos laterales de emergencias entre las bases. Resultando propicio si las bases vecinas se encuentran a distancias más cortas que el depósito central. Proporcionando un modelo de transbordos laterales en sistemas de inventario de revisión continua con reabastecimientos uno por uno y demanda poisson.

Los transbordos laterales dentro de un sistema de inventario son movimientos de existencias entre ubicaciones del mismo escalón. Estos transbordos se pueden realizar periódicamente en puntos predeterminados en el tiempo para redistribuir proactivamente las existencias, o se pueden usar de manera reactiva como un método para satisfacer la demanda que no se puede satisfacer con las existencias disponibles. Los elementos de un sistema de inventario considerados, p. Ej. el tamaño, las estructuras de costos y la definición del nivel de servicio, todos influyen en el mejor método de transbordo. Se han considerado modelos de muchos sistemas diferentes. Este artículo proporciona una revisión de la literatura que categoriza la investigación hasta la fecha sobre transbordos laterales, de modo que estas diferencias se puedan entender y se puedan identificar las lagunas dentro de la literatura.[⁶]. De igual manera en la siguiente investigación, se desarrolla un modelo analítico aproximado de transbordo de inventario de dos ubicaciones que combina el popular pedido-cantidad, punto de reorden (Q, R) revisión continua de la política de pedidos con un tercer parámetro, la cantidad retenida, que limita el nivel de transbordos salientes [⁷]. Es así, como la demanda irregular de la red de comunicaciones en logística humanitaria, especialmente después de un desastre natural a gran magnitud, presentan un desafío único para la modelización del inventario de socorro. Desarrollando un modelo de inventario de socorro humanitario en casos de desastre que asume una función distribuida uniformemente en los parámetros de tiempo de entrega y demanda [²].

El objetivo principal del estudio es investigar la inclusión de oportunidades de transbordo lateral en la cadena de ayuda humanitaria y examinar el efecto de diferentes parámetros para minimizar la distancia promedio recorrida por artículo mientras se atiende a los beneficiarios. El modelo de envío directo (DT), el modelo de transbordo lateral (LTSP) y el modelo de transbordo lateral marítimo (MLTSP) se desarrollan y comparan entre sí utilizando un escenario de terremoto de la vida real preparado para la ciudad de Estambul por JICA (Agencia Japonesa de Cooperación Internacional) [¹].

Para la investigación de Meissner,[⁸], examinaron los sistemas de inventario de ubicaciones múltiples bajo revisión periódica con múltiples oportunidades para transbordos proactivos dentro de un ciclo de pedido. Si se produce un desabastecimiento, la demanda se pierde sin posibilidad de realizar pedidos pendientes. El objetivo del modelo propuesto fue encontrar una política óptima que indique las fuentes y los destinos de los transbordos, así como el número de unidades, para maximizar el beneficio de la red. Crearon un programa dinámico que, en principio, puede resolverse de manera óptima utilizando la ecuación de Bellman. Sin embargo, el tamaño del estado y los espacios de decisión hace que sea imposible encontrar la política óptima para casos de problemas de tamaño real. Por lo tanto, se utilizó la programación dinámica aproximada hacia adelante para encontrar una política de transbordo casi óptima.

La logística humanitaria se ocupa de distintos desastres como terremotos, tsunamis, huracanes, epidemias, sequias, hambrunas, ataques terroristas y situaciones de guerra [⁹]; estos desastres plantean numerosos desafíos tanto para las personas afectadas como para las organizaciones que se encargan de planificar y distribuir los recursos adecuados, con el fin de satisfacer la demanda de la población afectada por un desastre natural o eventos inesperados que pueden ocasionar la destrucción, dicha operación resulta compleja, debido a que no es posible conocer con certeza y en tiempo real las necesidades de los damnificados. [¹⁰] y [¹¹] La logística humanitaria tiene el desafío de asignar recursos escasos a operaciones complejas de manera eficiente. Después de adquirir suficiente conocimiento contextual, los académicos pueden utilizar la investigación de operaciones (OR) para adaptar las mejores prácticas de gestión de la cadena de suministro a la logística humanitaria. Presentando dos casos de aplicaciones de quirófano para la gestión de flotas de vehículos de campo en operaciones humanitarias. Zhao, H., Deshpande, [¹²].

De igual forma, [¹³]Proponen un problema novedoso en logística humanitaria donde la demanda es dinámica debido al movimiento de personas entre nodos. Este problema es un punto de partida para considerar el comportamiento de las personas y los aspectos dinámicos en una red cuando un desastre golpea un territorio. [¹⁴] Consideraron el problema de diseño de un sistema logístico para asegurar la distribución adecuada de la ayuda de socorro en una situación posterior a un desastre natural, debido a que cuando los daños a la infraestructura pueden interrumpir la entrega de ayuda de emergencia.

II. METODOLOGÍA

Para considerar el modelo de estudio, se partió de una revisión de la literatura con el fin de conocer y explorar la gestión de inventario en logística humanitaria en la etapa post desastres. A partir de las temáticas estudiadas en la literatura, se identificó que en la comunidad científica proponen diferentes métodos para solucionar la gestión de inventarios ante un posible desastre natural.

Teniendo en cuenta lo anterior, se plantea un modelo de gestión de inventarios con transbordo lateral, permitiendo diseñar el modelo que describe la interacción dinámica entre albergues para suplir las necesidades, sirviendo como una nueva forma de apoyo al proceso de toma de decisiones en la etapa de post desastres.

Este artículo busca abordar los desafíos que conlleva la demanda estocástica de productos. siendo un estudio de caso que se ocupa de la distribución de las demandas de diferentes productos y utiliza la simulación Monte Carlo para administrar mejor su inventario.

El modelo propuesto, se estructuró teniendo en cuenta la revisión de literatura. Empezando con el modelo de transbordo lateral reactivo que buscan transbordar siempre que haya un desabastecimiento o un posible desabastecimiento, se adopta una teoría como es el sistema de inventario de revisión periódica. La política de revisión periódica revisa el inventario cada período de tiempo por no tener certeza de la demanda realizando un monto apropiado. En esencia lo que significa es un escenario probabilístico, variando el tamaña de pedido de acuerdo al comportamiento de la demanda.

En el caso de sistemas de inventarios con revisión periódica se utiliza la política (R, S), en donde R es el tiempo en semanas entre revisiones y S el nivel de inventario. Los sistemas están sujetos a una demanda, D, probabilística con tiempos de entrega, L, fijos para cada periodo. Las condiciones para cada escenario se fijarán en la sección de resultados. Se realizan los cálculos de inventario con entrega periódica y transbordo lateral para todas las semanas de la demanda con las que se realizó el estudio. En caso de ser posible se llevan a cabo los comparativos correspondientes. En este trabajo para el costo de inventario se tomará en cuenta: el costo de pedir el inventario y el costo de mantener el inventario.

Revisión periódica de pedidos

El modelo de inventario de revisión periódica, como se muestra en la Fig. 1, indica que hay un nivel predeterminado de inventario o inventario objetivo (TI) en cada depósito de inventario, rodeado de varios factores a saber: tasa de demanda (d), período de revisión (RP), plazo de entrega (L), y stock de seguridad (SS). La ecuación 1 muestra un cálculo del inventario de destino.

El propósito del buffer o margen que comúnmente se denomina stock de seguridad es reducir la fluctuación de la demanda durante la entrega de plazos. La ecuación (2) muestra un cálculo de stock seguro (SS) donde dos variables implicadas tales como: distribución normal z puntuación (Z) para cierto número de α nivel de confianza, y desviación estándar de la demanda (σ_{RP + L}).

Se lleva a cabo la entrega de los artículos necesarios o el punto de reordenación cada tiempo del período de revisión. El importe de los artículos (Q) que se transportan para cada reabastecimiento se calcula utilizando la ecuación (3) en el que el inventario objetivo (TI) se resta por el nivel de inventario de alquiler de curación (OH).

Se plantea el problema del transbordo lateral en una formulación matemática simple. El modelo consta de tres elementos (U, T, R) donde U es un conjunto de puntos de albergue, T es una topología que conecta las unidades y R es un conjunto de reglas de interacción entre albergues. Un conjunto de albergues U es un número finito de albergues. La topología del sistema de inventario de transbordo lateral es una red libre de escala. Se restringe el caso en el que cada albergue tiene un estado: normal (1), anormal (0). Cada albergue ayuda a los otros albergues de forma sincrónica. La ayuda tendrá éxito si el nivel de inventario actual más la proporción compartida por otro albergue es mayor que el umbral normal estándar (N). La proporción compartida por el albergue en estado normal es Pn, mientras que la proporción compartida por el albergue en estado anormal es Pa en la que Pa < Pn. El valor de la proporción de Pn y Pa varía de 0 a 1. El albergue ayudado aumentará su estado cuando todas las reparaciones sean exitosas. N y A es el umbral de proporción del estado de la unidad normal y anormal, mientras que I represento una proporción del nivel de inventario actual. Hay varias suposiciones utilizadas en este modelo [⁵].

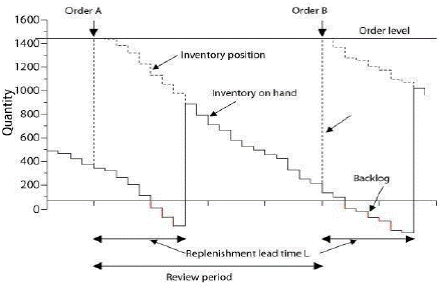
Fig. 1 Modelo de revisión periódica. Nota: el gráfico representa un modelo de inventario empleando revisión periódica. Tomado de [⁵]. 

En el modelo propuesto, se usa una proporción en lugar de probabilidad debido al proceso de cambio de estado de las unidades, en este caso los albergues, es claramente visible. Las reglas de transición para los cambios de estado por unidad auxiliar son las siguientes:

Las reglas de transición para los cambios de estado por unidad ayudada si la ayuda por unidad normal son las siguientes:

Las reglas de transición para los cambios de estado por unidad ayudada si la ayuda por unidad anormal son las siguientes:

III. RESULTADOS Y DISCUSIÓN

En esta sección, se evalúa el transbordo lateral de artículos humanitarios mediante simulación numérica. La simulación numérica se contrae utilizando datos sintéticos, para efectos de la simulación de la demanda se tomó una capacidad de un albergue, y así obtener un promedio de ayudas por semana con un coeficiente de variación y una desviación estándar. Una vez, teniendo la simulación de la demanda se ejecuta el modelo de revisión periódica permitiendo determinar la cantidad de ayudas requeridas durante un periodo, y a través de la revisión periódica el modelo asignará las ayudas necesarias para evitar desabastecimiento en ese punto. Esto con el fin de cumplir las actividades en un tiempo adecuado para satisfacer las necesidades y el bienestar de la población.

En cuanto al modelo de transbordo lateral, se hace necesario encontrar parámetros apropiados para el modelo que mejore el rendimiento del inventario. Teniendo en cuenta la variación de parámetros como el Pn y Pa y así, observar el efecto del inventario en un albergue después de brindar ayuda humanitaria a un albergue vecino. Y, además, como un albergue que recibe ayuda de otro se beneficia para atender una emergencia.

A continuación, se plantea dos escenarios como es la entrega periódica desde un centro de distribución y la entrega periódica con transbordo lateral. Y así, permitiendo evaluar el efecto del transbordo lateral en la mejora del rendimiento del inventario en un albergue.

Se observa la simulación Monte Carlo para el modelo de inventario periódico, la cual hay una revisión de inventarios de la manera más minuciosa posible, tomando en cuenta factores que causan posibles desabastecimientos en las existencias o retrasos en su reposición, la simulación genera la espera de rangos de tiempos entre las revisiones del inventario, las mismas que deben realizarse en períodos de tiempos iguales, por ejemplo: la incertidumbre de la demanda aumenta la posibilidad de rotura de stock. Un método para reducir la posibilidad de rotura de stock, es considerar un margen de seguridad que brinde un soporte entre el tiempo de revisión y entregas.

Por lo tanto, un modelo de inventario probabilístico hace uso de una distribución normal de probabilidad para especificar el valor de la demanda o de otra variable desconocida, teniendo en cuenta un coeficiente de variación y la desviación estándar para simular la demanda promedio durante 52 semanas. El inventario será revisado de forma periódica (cada dos semanas) y no de forma continua, por lo que la emisión de pedidos se realiza al final de cada período, teniendo un plazo de entrega de una semana. Partiendo de varios supuestos como:

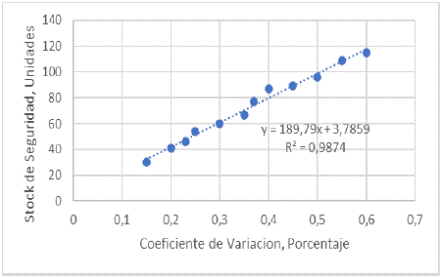
Lo primero es variar el cálculo del coeficiente de variación y así, identificar como entre más variabilidad de la demanda, el stock de seguridad aumenta de manera lineal.

Para encontrar la relación de cambio entre el coeficiente de variación y el stock de seguridad, se generan los resultados que se muestran en lafig. 2, en la que puede verse que la relación entre el coeficiente de variación y el stock de seguridad es directa y lineal, aumentando el stock de seguridad 189.79 unidades por cada porcentaje de incremento del coeficiente de variación, lo cual era de esperar. En la figura se ha incluido el ajuste de la relación con su valor de R cuadrada, que señala que ha sido un muy buen ajuste entre las variables.

Fig. 2 Relación del stock de seguridad con el coeficiente de variación.  

Fig. 3 Evolución de los niveles de inventario en el tiempo. 

Seguidamente, se plantea la simulación en la que se evidencia la entrega periódica desde un centro de distribución al punto de albergue. Teniendo en cuenta los parámetros antes mencionados, la simulación se realiza con un coeficiente de variación del 0.35 permitiendo una variabilidad de la demanda de forma significativa y dejando un stock de seguridad alto para evitar posibles roturas de stock en los periodos de demanda. Generalmente un sistema de revisión periódica exige un nivel más alto de inventario de seguridad en comparación con el nivel de revisión continua. En este contexto y para tener una mejor idea de la evolución de los niveles de inventario en el tiempo el modelo de revisión periódica se muestra en la fig. 3.

Se considera que el centro de distribución que abastece los inventarios a los albergues, toma las órdenes de pedido cada dos semanas. Se asume adicionalmente que elTiempo de Reposición o Lead Time (L)es fijo y corresponde a una semana. El gráfico anterior muestra que los pedidos son realizados cada intervalo de tiempo fijos (T) y la reposición tarda exactamente L unidades de tiempo en ser recepcionadas. Notar también que el tamaño de los pedidos es variable y está influenciado por el volumen de productos que se dispone en inventarios al momento de emitir el pedido. Luego bajo este esquema no siempre se podrá abastecer la totalidad de la demanda durante el período de reposición, debido a la incertidumbre de la demanda en una situación de desastres naturales. (Por lo cual lo mejor que se puede hacer es establecer niveles de stock de seguridad como meta para evitar desabastecimientos futuros).

Ahora bien, se plantea el modelo de transbordo lateral con entrega periódica desde el centro de distribución, evidenciando como afecta el comportamiento del albergue una vez haya prestado ayuda a un albergue vecino para satisfacer la demanda. Para el modelo de transbordo lateral se tendrá en cuenta parámetro de decisión como el Umbral de Proposición del estado normal (N), Umbral de proporción del estado anormal (A), proporción compartida por el estado normal (Pn) y la proporción compartida por el estado anormal (Pa). En el cual, se podrá observar el estado del albergue a través del tiempo viéndose afectado al brindar la ayuda al albergue vecino más cercano. Con una proporción de ayuda del estado normal (Pn = 0.2) y una proporción de ayuda del estado anormal (Pa = 0.1).

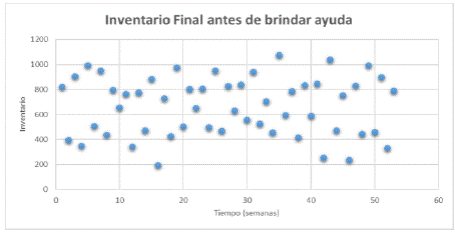
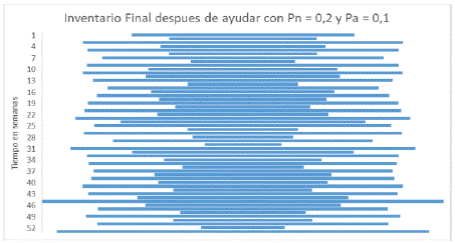
A continuación, en la fig. 4 se establece como está el nivel de inventarios en un albergue antes de brindar una ayuda a otro albergue vecino en un periodo de 52 semanas, teniendo un rango disponible de inventario entre 200 y 1100 en el transcurso del período. En la fig. 5, se puede observar como este rango de inventario disminuye afectando levemente el nivel de inventario durante el periodo de simulación. Cabe aclarar, que para esta simulación se utilizó un Pn = 0.2, Pa = 0.1 con en N = 0.7 y A = 0.3.

Fig. 4 Inventario final antes de brindar ayuda en un tiempo de 52 semanas. 

Fig. 5 Inventario final después de brindar ayuda en un tiempo de 52 semanas. 

Fig. 6 Inventario final después de brindar ayuda con un Pn = 0.2 y Pa = 0.1. 

Fig. 7 Inventario final después de brindar ayuda con un Pn = 0.5 y Pa = 0.2. 

Fig. 8 Inventario final después de brindar ayuda con un Pn = 0.9 y Pa = 0.5. 

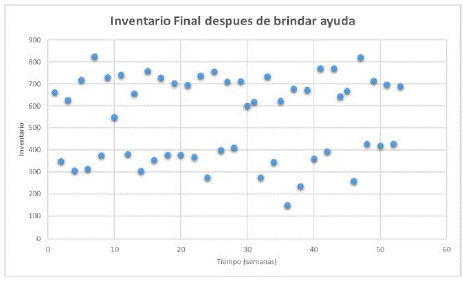
Así mismo, para efectos de probar el inventario final después de brindar ayuda se realizó una variación en las proporciones de ayuda de un estado normal y anormal. En la fig. 6 se utiliza un Pn = 0.2 y Pa = 0.1, esto conlleva a que, a menor proporción de ayuda el nivel de inventario en cada periodo se mantendrá óptimo para seguir satisfaciendo la demanda.

Caso contrario, al realizar la simulación con un Pn = 0.5 y Pa = 0.2, el nivel de inventario disminuye en comparación con la figura anterior, también puede ocurrir desabastecimiento en algún periodo. Esto debido a que la proporción de ayuda de un estado normal es alta y tendrá que compartir más artículos para ayudar a sus albergues vecinos fig. 7.

La fig. 8, muestra una ayuda proporcionada por el albergue conlleva a tener el nivel de inventario bajo y desabastecimiento en varias semanas después de brindar ayuda.

A continuación, en fig. 9 se observa el estado de un albergue antes de recibir la ayuda de su albergue vecino, las líneas azules indican un estado normal (1), es decir un nivel de inventario alto, indicando con esto que sin el transbordo lateral el albergue presenta en varios periodos (semanas) estados anormales (0). Poniendo en riesgo un posible desabastecimiento.

Fig. 9 Estado de Un Albergue antes de recibir ayuda. 

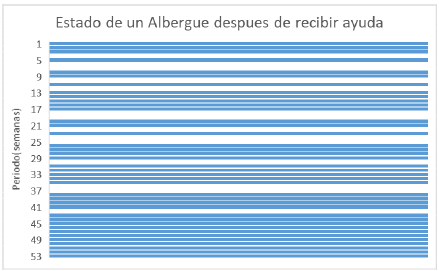
Caso contrario, sucede cuando a ese mismo albergue le llega ayuda mediante el transbordo lateral, como lo muestra la fig. 10 los estados normales (líneas azules) son más debido a esa ayuda recibida. Dejando en evidencia que el transbordo lateral tiene una ayuda significativa para evitar posibles desabastecimientos.

Fig. 10 Estado de Un Albergue después de recibir ayuda. 

Los resultados de la simulación numérica muestran que en comparación con el modelo tradicional (sin transbordo), el modelo de inventario con transbordo lateral de stock entre albergues tiene un efecto positivo para reducir el desabastecimiento. La proporción de ayuda del estado normal y anormal se aplica en un 0.2 y 0.1 respectivamente, teniendo un efecto favorable en cuanto al nivel del inventario durante el periodo de tiempo como lo muestra la fig. 6. Caso contrario en las figuras 7 y 8 se evidencia, que el nivel de inventario disminuye al tener una proporción de ayuda más alta.

Cabe resaltar, que el transbordo lateral tiene un resultado positivo en lo que se refiere a la recepción de la ayuda durante el periodo, esto se evidencia en la fig. 10 que indica el estado del albergue después de recibir la ayuda, mostrando que la mayoría del tiempo el nivel del inventario se encuentra en un estado normal.

IV. Conclusiones

Este estudio se ha realizado para determinar si las variaciones de la demanda de los consumidores afectan al inventario de seguridad requerido, conforme a lo señalado por [15], lo cual ha quedado confirmado.

Con mayor variabilidad de la demanda del tiempo de entrega, las existencias de seguridad aumentan, a razón de 189.79 unidades por cada porcentaje de incremento del coeficiente de variación para el artículo con distribución normal. Esto va de acuerdo a lo que la mayoría de los académicos ha encontrado en otras investigaciones [16].

El transbordo lateral sin reconocimiento del nivel de inventario ha demostrado tener un ligero impacto positivo en la per-formación del sistema de inventario durante un desastre donde la demanda y la información de plazo de entrega están muy sesgadas. Este sistema puede aprovechar el número de existencias entre los albergues. Las investigaciones futuras de esta área pueden dirigirse al transbordo lateral en el que se asume posible el reconocimiento del nivel de inventario para cada albergue. La integración con la planificación logística también puede ser una de las principales preocupaciones para el desarrollo futuro.