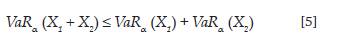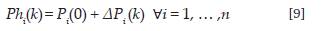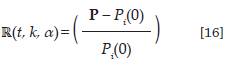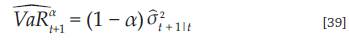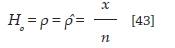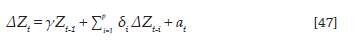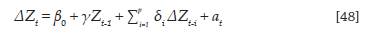1. Introducción
La actividad de compra y venta de deuda pública es una de las más dinámicas del mercado de capitales en Colombia, país que desde hace muchos años ha venido financiando sus gastos a través de este mecanismo, que ha sido muy atractivo tanto para los inversionistas locales como internacionales.
El estudio del valor en riesgo es uno de los temas más abordados en la literatura nacional e internacional, en donde se han identificado por el mercado diferentes metodologías, las cuales miden cuál sería el monto máximo que estaría dispuesto a perder un inversionista si mantiene en su portafolio un papel de renta fija o variable.
El trabajo que se presenta se compone de cinco partes: en primer lugar, antecedentes del mercado de deuda pública; segundo, conceptualización del valor en riesgo; tercero, aplicación de las metodologías del valor en riesgo en el mercado de deuda pública; cuarto lugar, análisis descriptivo estadístico del mercado de deuda pública y estimación del valor en riesgo VaR en el mercado de deuda pública, para terminar con las conclusiones y recomendaciones a trabajos futuros.
2. Antecedentes del mercado de deuda pública
A principios de la década de los noventa, la colocación de títulos de deuda pública en América Latina se caracterizó por un crecimiento débil concentrado en la búsqueda de recursos en los mercados internacionales frente a un limitado desarrollo de sus mercados de deuda.
En Colombia, el mercado de deuda pública se encuentra conformado por papeles colocados tanto en el mercado local como en los mercados internacionales. A nivel del mercado local, el saldo en el periodo 2011-2014 ascendió en TES2 tasa fija clase B a 129.272 millones de COP, en tanto que en TES UVR ascendió en el periodo señalado en 42.642 millones de UVR.
A continuación, se muestra el saldo de TES en el periodo 2011-2015
Como se puede visualizar en la figura 1, el saldo la tasa de crecimiento en los saldos de TES de clase B mostró un crecimiento del 6,4 % en tasa fija y de un 15,3 % en UVR, como consecuencia de la entrada de nuevas emisiones al mercado como los TES de fecha de vencimiento mayo/17, agosto/26 y septiembre/30 entre otros.
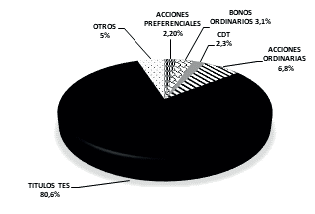
En el mercado de valores de Colombia, los papeles de renta fija presentan mayor volumen de negociación que los otros papeles del mercado con una participación del 82,9 % entre los que sobresalen los TES con un nivel del 80,6 %, como se puede visualizar en la siguiente figura:
En lo que atañe a los indicadores de deuda interna y externa, tanto en duración3 como en cupón promedio presentaron un comportamiento en promedio de 3,88 y 9,25 %, respectivamente a nivel local, mientras que a nivel externo muestra 5,08 y 5,87 % cada uno, como se muestra en la siguiente figura 2:
Como se puede visualizar en la figura 3, la duración de los papeles de renta fija a nivel local TES ha ido aumentando, en tanto que el cupón promedio ha oscilado entre un 7,50 % a un 9 % (MinHacienda, 2016).
3. valor en riesgo
Matemáticamente, el valor en riesgo corresponde al cuantil (1 - α) de la distribución conformada por las pérdidas y ganancias P/G, donde esta es continua y de manera monótona.
Este estimador denota el cambio en el valor de la cartera como q(p), así la probabilidad expresada como P(q(p)<VaR) = 1 - α, se maneja estrictamente al nivel de confianza a previamente establecido.
El VaR está definido por los siguientes conceptos:
1. Dada una distribución de pérdidas y ganancias
donde X T es definido en un tiempo futuro y a un nivel de confianza a previamente establecido. ( Embrechts, 2016).
2. Se escribe el VaR en forma de cuantil de la distribución P/G como
3. Con lo anterior se escribe a un nivel de confianza a e (0,1), el valor correspondiente al nivel de confianza previamente establecido por la distribución.
Debido a esta previa introducción es que se puede nombrar al valor en riesgo como un cuantil de la distribución P/G asociado a este. El nivel de confianza ronda típicamente entre 0.95 y 0.99 para el caso del riesgo de créditos y de mercado, y 0.999 para el riesgo operacional (P. E. y Hóing, 2006).
Uno de los aspectos más importantes del VaR es tener en cuenta la parte cuantitativa del manejo de riesgo sin descuidar aspectos cualitativos, esto genera la posibilidad de ser una gran fuente de comunicación entendible y cultamente aplicada.
El valor en riesgo aun cuando sea una de las medidas más usadas por sus buenas estimaciones y ser entendible, requiere de ciertos aspectos que se deben observar al hacer su cálculo. Según Embrechts (2016), el VaR se caracteriza por ser una medida de frecuencia, lo que no la hace muy robusta; aparte de esto sufre problemas a cuantiles, que dificultan los resultados; por otro lado, arroja intervalos de confianza muy abiertos lo cual causa un problema de confiabilidad a la hora de hacer las estimaciones. En consecuencia, se hace necesario entrar en detalle y mirar con bastante sutileza los cálculos proporcionados, además de dar detalle al comportamiento del mercado.
3.1 Teoremas matemáticos sobre el VaR
Algunas características importantes sobre el valor en riesgo se han mencionado anteriormente; sin embargo, es necesario hacer hincapié en sus propiedades que han definido a este método como lo conocemos hoy en día.
■ Subaditividad
La paradoja de Banach-Tarski dice que dados unos subconjuntos acotados α, β ⊂ Rd, d≥3, int(α)≠∅ y int(β)≠∅; por lo tanto, existen subparticiones en estos subconjuntos α=α1∪ … ∪αk, β = β1∪ … ∪β k , tales que αi y βi sean congruentes.
En otras, la subaditividad provoca efectos de diversificación.
Es común ver esta propiedad en entidades bancarias con obligaciones de deuda colateralizada4 y MBS (valores respaldados por hipotecas).
Por otro lado, es bastante factible para portafolios con comportamiento normal multivariado y portafolios con características elípticas. Sin embargo, es una medida insuficiente cuando se poseen colas pesadas en la distribución de los datos, sesgo en la información y distribuciones marginales con dependencias específicas.
■ Súperaditividad
Tomando en cuenta lo anterior, el VaR cuanta con otra propiedad: la súper-aditividad, esto tomando en cuenta la tenencia de colas pesadas en la distribución de los datos, que provocan problemas de modelos con media infinita, lo cual indica que para X 1 y X 2 la probabilidad
 (modelos de media infinita), el VaR se convierte en súperaditivo para niveles de confianza altos:
(modelos de media infinita), el VaR se convierte en súperaditivo para niveles de confianza altos:
Así, va generando un índice de concentración,
Por último, el VaR cuenta con un buen uso en el riesgo del mercado financiero, aunque posee algunas restricciones en el riesgo de crédito, así como un comportamiento no normal en algunas plataformas del mercado y es bastante bueno y dinámico en el manejo de modelos cuantitativos para la administración del riesgo.
Para hacer uso del valor en riesgo hay que partir desde varios métodos, que así van generando distintos puntos de vista frente a las observaciones y resultados estimados; los métodos más usados para el cálculo del VaR son la simulación histórica, método de Montecarlo, EWMA y la obtención de la distribución de P/G a través de modelos Egarch, Arma-Garch, GJR-Garch, entre otros.
4. MODELOS DE ESTIMACIÓN DEL VALOR EN RIESGO APLICABLES AL MERCADO DE DEUDA PÚBLICA
A continuación, se describen a nivel teórico los modelos de estimación del valor en riesgo aplicables al mercado de deuda pública:
4.1 Simulación histórica
Actualmente se puede encontrar una gran cantidad de métodos para estimar el valor en riesgo (VaR) de un portafolio, de acuerdo con lo citado en Li, Fan, Li, Zhou y Liu (2014), en la encuesta hecha por Pernigón y Smith en 2009 se encontró que el 73 % de los bancos de Estados Unidos y Canadá desde 1996 hasta 2005 han usado metodología para la estimación del VaR basadas en la simulación histórica y acercamientos por el método de Montecarlo.
Según Finger (2006), las entidades bancarias optan por el uso de la simulación histórica ya que responde bastante bien a las siguientes observaciones:
Es fácil de explicar.
Es un método conservador.
Es libre de supuestos.
Logra capturar colas pesadas en la distribución.
Expone de manera precisa donde puede haber errores.
Logra obtener buenos pronósticos.
Debido a todos estos aspectos, es lógico que se haya usado bastante este método por los bancos; sin embargo, es necesario ver más allá históricamente para encontrar porque continuan haciéndolo.
Según Holton (2015), durante la década de los noventa se generó una migración de intelectuales en el área de las matemáticas y de la física de la industria militar hacia Wall-Street, quienes con sus habilidades desarrollaron productos financieros mientras creaban estrategias de precios y cobertura; sin embargo, como en su implementación no se consideró el impacto que tendría en el manejo de riesgo financiero, se delegaba la ejecución de las operaciones financieras a personas menos capacitadas en el manejo de este tipo de mediciones.
Ante la situación presentada, anteriormente se optó por el uso de la simulación histórica al ser poco sofisticada a nivel matemático y así cada persona podría entender esta metodología de manera sencilla. Ante esta preferencia los reguladores bancarios aceptaron dicha propuesta de cálculo contratando los servicios de consulta en riesgo a entidades como J.P Morgan con RiskMetrics, y Cs First Boston con PrimeRisk entre otros (Holton, 2015).
En lo que concierne a la simulación histórica, consiste en un método de incorporación predictiva del riesgo que incluye una distribución de probabilidad acumulada de los retornos y su volatilidad. Una manera de clasificar este método está en sus supuestos no paramétricos, es decir, por el uso asintótico de la distribución empírica, teniendo pérdida en asumir una distribución ligada a los retornos.
El método de simulación histórica presenta una valoración total en donde su uso se realiza mediante la aplicación de los pesos actuales de las series temporales en los rendimientos históricos.
Para el cálculo del VaR mediante esta metodología, es necesario tanto el conocimiento de los precios de las variables de mercado, que son los factores de riesgo de un periodo anterior, como el cálculo de las variaciones porcentuales diarias de cada uno estos.
A continuación se hace necesario aplicar los retornos diarios al valor corriente de cada activo y realizar su suma. Con este número se identifica la variación del valor de la cartera en el día d y a través suyo es posible realizar k cantidad de simulaciones o escenarios para identificar de alguna forma el comportamiento diario del portafolio de inversión.
Después de realizar el planteamiento procede dar orden a los cambios diarios del valor del portafolio ordenados ascendentemente, con lo que se encuentra una función asociada a las variaciones diarias del valor del portafolio.
Al final, se debe utilizar un nivel de confianza deseado calculando el cuantil de la distribución conformada por las pérdidas y ganancias P/G (Menichini, 2006).
Matemáticamente, el VaR a través del método de crecimientos absolutos se obtiene de la siguiente manera:
Se deben aplican los pesos actuales de la serie presente a la serie de rendimientos de los activos históricos:
donde los pesos actuales p i . dependen del tiempo t y Ri de k; a través de esto construimos un escenario pertinente para la construcción histórica.
Se requiere una valoración construida generalmente por la totalidad de los precios completos incluyendo rendimientos exactos y todas las cuervas de crecimiento. Luego de esto es preciso obtener los precios futuros mediante la simulación de n cantidad de escenarios utilizando los cambios históricos de cada uno de los precios para aplicarlos en los actuales:
donde el ΔPi (k) corresponde a la diferencia de precios entre el día i y el día i-1 P/G diaria.
Se hace necesaria la creación de una variable hecha como el conjunto de precios correspondiente a los escenarios T(α,k = 1, ... ,t), y que comporta un nuevo valor de la cartera. Luego calculamos un riesgo con volatilidades cambiantes de forma implícita creando un rendimiento conforme a un escenario específico k simulado:
donde R(t, k, α) es el rendimiento simulado en el día t y T(α, k) corresponde a los escenarios en el día t.
A través de todo esto encontramos la distribución correspondiente a los rendimientos en el k escenario y calculamos el cuantil (1 - α) correspondiente al VaR.
Según li et al. (2004) se puede ver la implementación de este método mediante otra perspectiva, en donde se escribe la serie de los retornos como
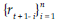 calculando la siguiente estimación para el VaR así:
calculando la siguiente estimación para el VaR así:
donde Per denota el percentil de la distribución de los retornos calculada mediante la simulación y r t los retornos del portafolio en el día t.
4.2 Simulación histórica con crecimientos logarítmicos
Esta metodología es igual a la anterior, pero teniendo en cuenta los rendimientos de forma logarítmica para así calcular el rendimiento de los precios como:
donde P i .(t) corresponde al precio en el día t y P i .(t - 1) el precio en el día t - 1.
Posteriormente a este cálculo es necesario la creación de una serie de tiempo con los escenarios simulados multiplicando los escenarios recientes o actuales con el rendimiento logarítmico de los precios más una unidad:
Luego se realiza la serie, a apartir de los rendimientos simulados con los rendimientos de los precios, y tomando en cuenta las observaciones recientes:
Una vez obtenidos los rendimientos simulados se calcula el VaR tomando el cuantil ( 1 - α) con el nivel de confianza seleccionado.
4.3 Simulación histórica con crecimientos relativos
Este método de simulación se basa en calcular los rendimientos históricos como el cociente de los precios recientes para un día t
Después de obtener los rendimientos de los precios, es necesario calcular los precios simulados, para así realizar el cálculo de rendimientos aritméticos conforme a los escenarios simulados, utilizando los precios recientes o finales para realizar su cociente:
Al obtener los rendimientos aritméticos simulados se tiene la distribución correspondiente para el cálculo del valor en riesgo de la misma forma: utilizando el cuantil (1 - α) al nivel de confianza seleccionado.
Teniendo en cuenta los objetivos de este trabajo, es necesario hablar de los aspectos paramétricos para la estimación del VaR, pues se requiere precisar el uso de supuestos en cuanto a la distribución de probabilidad que caracteriza los valores posibles de los factores de riesgo asociados al respectivo portafolio de activos financieros. Según Powell (2014), al implementar el teorema del límite central en 1900 Bachellier logró estandarizar los precios de las acciones de la bolsa de París descubriendo que ante los cambios excesivos de los montos de los portafolios se lograba obtener una distribución normal. Desde este momento se hizo ese supuesto de distribución a muchos de los comportamientos accionarios.
Los aspectos cruciales en los métodos paramétricos se encuentran en calcular la media y desviación estándar de la distribución normal que se asume con las series propuestas por los datos históricos; al tener estos supuestos de normalidad en los datos solo se procede a calcular el cuantil de la normal correspondiente al nivel de confianza deseado encontrando el valor en riesgo (Join, 2001; Moscote, 2013).
■ Simulación Montecarlo
La simulación de Montecarlo es el método más usado después de la simulación histórica para la estimación del valor en riesgo; su uso se enfoca en ver las probabilidades de pérdidas al exceder un valor especifico en la distribución supuesta. Así, este método propone que los factores de riesgo del respectivo portafolio de activos financieros son dados a través de una distribución cualquiera (Li et al., 2014):
Con referencia a los supuestos teóricos, estos recaen en la teoría de la probabilidad en la simulación, pues se realizan k-escenarios en donde se asume una distribución de probabilidad conocida para los precios, mientras que al darse algunos procesos se obtiene una distribución de probabilidad con la que se estimará el VaR a cierto cuantil, tomando en cuenta que los precios y su parámetro son variables aleatorias con alguna distribución de probabilidad a encontrar.
Por otro lado, esta metodología parte de supuestos sobre los procesos estocásticos inherentes con el movimiento geométrico browniano, a fin de encontrar el método que caracteriza la aleación de la distribución de probabilidad de los precios con la distribución final para la estimación del VaR ( Powell, 2014).
Con la estimación del VaR utilizando el método de Montercarlo, se pueden caracterizar varias distribuciones para las variables de interés y modificarlas en el caso requerido. Una vez hechos los supuestos de distribución es necesario implementar los escenarios donde las variables de riesgo del mercado toman diferentes consecuencias de acuerdo con el valor de cartera que estas reflejan.
Con posterioridad al resultado de las realizaciones hechas por los k-escenarios, se obtiene la distribución de los retornos dados por el portafolio utilizando un proceso estocástico en donde se procede a calcular el cuantil correspondiente al VaR a un nivel deseado.
El contraste de la simulación histórica demanda el uso de datos históricos mientras se realiza la distribución de probabilidad de los retornos; sin embargo, con el método de Montecarlo se pueden hacer varios juicios sobre la distribución de las variables y traer información adicional para mejorar tal aspecto (Powell, 2014).
Así mismo, la estimación del VaR para un solo activo financiero obliga a identificar de primera mano el proceso estocástico de movimiento geométrico browniano, que sigue la siguiente terminología:
donde ξ,
t
corresponde a los precios en el tiempo
 es el retorno esperado (µ la media de los retornos esperados y θ
2
su varianza ), Δt es el incremento diario, y θt~N(0,1) es la aleatoriedad dada en el tiempo t y que permite el cambio continuo en los precios.
es el retorno esperado (µ la media de los retornos esperados y θ
2
su varianza ), Δt es el incremento diario, y θt~N(0,1) es la aleatoriedad dada en el tiempo t y que permite el cambio continuo en los precios.
Reordenando el proceso estocástico de movimiento geométrico browniano, se puede obtener el siguiente término correspondiente a los retornos:
A partir de la ecuación anterior, es necesaria la implementación de un conjunto de números seudoaleatorios provenientes de una distribución normal con media estándar, para modelar el proceso estocástico utilizando el método congruencial lineal:
Donde α debe ser mayor a 0 y M es el módulo tal que M>α; estos números representan las probabilidades de los posibles eventos que pueden ocurrir a cierta cantidad de cambios en los retornos. Al obtener estos números se hace necesaria su transformación en θ
t
~ N(0,1), y se procede a la implementación del proceso estocástico generándolos un número k de veces, donde el número mínimo de realizaciones depende de cuán precisa quieren ser las estimaciones arrojadas por la simulación
 donde A = y - µ, y corresponde a los valores simulados y [i la media de la distribución del factor de riesgo (Powell, 2014).
donde A = y - µ, y corresponde a los valores simulados y [i la media de la distribución del factor de riesgo (Powell, 2014).
Finalmente se calcula con el movimiento geométrico browniano los valores correspondientes a los retornos ℝ t+Δt , para luego sí calcular el VaR al nivel (1 - α) de confianza seleccionado donde a usualmente se utiliza al 5 %.
El anterior caso solo tuvo un activo de un portafolio de inversión; sin embargo, para el cálculo del VaR, utilizando un portafolio de inversión conformado por varios activos financieros, es necesario el uso de las matrices de varianzas y correlaciones conformada por los distintos activos.
Al tener las respectivas matrices de varianza y correlación se multiplican de tal forma que quede una matriz varianza-correlación única; después está se multiplica por la matriz de varianza a efectos de construir la matriz de varianzas y covarianzas, para luego realizar la ponderación respectiva con los precios establecidos.
Una vez construidas las matrices anteriores se suma la diagonal de la matriz de varianzas y covarianzas ponderada, para encontrar la desviación estándar del portafolio, y así finalmente calcular el VaR a un nivel (1 - α) de confianza seleccionado utilizando la media de los retornos y su desviación.
■ Modelos EWMA y EQWT
Los modelos EWMA y EQWT utilizan acercamientos por el método de varianzas-covarianzas, en donde se asume que los factores de riego que determinan el valor de un portafolio de inversión son distribuidos de manera normal multivariada, lo que implica que el VaR del portafolio es un múltiplo de la desviación estándar:
Donde w es el vector con los pesos del portafolio, Σ la matriz de varianzas-covarianzas y θ un factor de expansión, el método de varianzas y covarianzas supone los retornos de un portafolio ℛ hecho con m precios, tales que:
donde δ i . se le conoce como pesos de la serie y a R i como una variable aleatoria con la matriz de varianzas y covarianzas Cov(R v R) - σ i σ j ξ if . Con lo anterior se puede aproximar el VaR de la siguiente manera:
donde µ i , σi 2 corresponden a la media y varianza de los retornos, y se estiman bajo máxima verosimilitud. Por medio de las varianzas y covarianzas de la matriz se estiman las series históricas de los retornos del portafolio usando unidades de media movible iguales (EQWT) (Raaj y Rauning, 2005):
donde σij 2 denota los elementos de la matriz de varianzas-covarianzas en un tiempo especifico, y p it p jt los retornos.
Esta aproximación histórica EQWT presenta dos pasos:
A partir de lo anterior, se calculan los retornos ponderados para el periodo de tiempo de la serie y se toma la ratio logarítmica de los precios del portafolio de inversión:
donde los retornos se calculan en el periodo T i al número de factores de riesgo m. Posteriormente a estos pasos se calcula la varianza de los retornos al cuadrado:
Al ser esto una media de los retornos R i , bajo un peso igual se puede escribir el factor de expansión θ.
Como el método EQWT posee siempre el mismo factor de expansión (pesos), la metodología EWMA toma en cuenta un mayor peso en esta varianza ocasionando mayor influencia en los retornos. Esta diferencia se da específicamente en que en la metodología EWMA (exponentially weighted moving averages) los pesos de las observaciones están dadas bajo un tipo de suavizamiento exponencial. Una forma abreviada de ver esta metodología se puede escribir de la siguiente manera:
donde λ es conocido como un parámetro de suavizamiento y es menor que uno; usualmente este factor de decaimiento toma valores entre 0.95 y 0.99 lo que implica que a factores de decaimiento bajos estos tiendan a datos ponderados por los pesos de mayor manera. A diferencia de los pesos de la metodología EQWT, los pesos en la varianza son diferentes como se expresa a continuación:
Una diferencia particular metodologíca entre los dos métodos de estimación es que EQWT no toma en cuenta la dependencia de las variables en el tiempo, mientras que los modelos EWMA sí tienen en cuenta este tipo de comportamiento.
■ VaR paramétrico
El cálculo del VaR a través de metodologías paramétricas sigue un acercamiento tradicional en cuanto a los supuestos de normalidad que siguen los portafolios. Esta metodología utiliza los factores de la matriz de varianzas y covarianzas junto con el modelo proporcionado por los retornos a manera de variables aleatorias, con distribución normal.
Las únicas variables necesarias para el cálculo del VaR paramétrico son la media y desviación estándar del portafolio y así mismo el cálculo del valor de la normal estándar a un nivel de confianza seleccionado; el cálculo del VaR se puede ver de la siguiente manera:
donde µ es la media y o la desviación de los retornos.
En la práctica, este método es bastante riesgoso debido a los supuestos de normalidad ya que usualmente no se tiene una evidencia observacional para determinar si este hecho es factible. En otro aspecto el VaR paramétrico también impone la restricción de precios lineales, lo que no es adecuado para los valores altamente no lineales (Bloomberg, 2016). Otro problema que posee este método está en la estabilidad de la desviación estándar a lo largo del tiempo, por lo que estos valores extremos tienden a subestimar el VaR y pueden generar una exposición a riesgo mayor a la de otras metodologías.
■ VaR histórico
Esta metodología modela las colas pesadas de los retornos usando la distribución histórica de estos en vez de asumir que se distribuyen normalmente. En este método, la distribución conjunta de los retornos es representada por un panel de retornos diarios históricos a lo largo de varios años, para así simular los respectivos rendimientos mediante las colas de la distribución t-student, cuyas desviaciones estándar son estimaciones de las volatilidades del portafolio. Para calcular el VaR es necesario organizar descendentemente los retornos históricos y computarlo con un nivel de confianza al retorno menor.
En contraste con el VaR paramétrico, el Var histórico captura las colas pesadas de la distribución de los retornos del portafolio y ofrece flexibilidad para las múltiples técnicas de evaluación de las metodologías; en contraste con el método de Montecarlo, el VaR histórico tiene la ventaja de no asumir una distribución para los retornos utilizando la distribución histórica de estos por lo que lo convierte en un método fácil de calcular e interpretar. Por otro lado, se puede cuestionar la fidelidad de utilizar la distribución histórica de la distribución de rendimientos futuros debido a las condiciones del mercado ya que actualmente no son como han sido en el pasado. Otro problema de esta metodología está en la limitación en la longitud de los datos proporcionados ya que un pequeño número de escenarios históricos tiende a tener una confianza menor en la estimación del VaR.
En la siguiente tabla se puede encontrar una clasificación para las metodologías paramétricas:
■ Modelos de volatilidad
La estimación del VaR con supuestos normales evidencia en la aplicación una presencia amplia de sesgo y curtosis lo que resulta en poca o mucha cobertura de las estimaciones calculadas. Por lo tanto, asumir otro tipo de distribuciones y realizar modelos para el manejo de riesgo resulta en muchas ocasiones un factor óptimo en la estimación oportuna del VaR.
En la práctica, es bastante común utilizar modelos autorregresivos de heterocedasticidad condicional (ARCH) y generalizados (Garch), ya que estos capturan los movimientos no constantes de la varianza a través del tiempo luchando contra los constantes cambios en la volatilidad. En la práctica, los modelos más utilizados de esta clase son los ARCH (1), Garch (1,1) y Egarch (1,1); en el caso de este documento, se estimará el VaR por medio del modelo Garch (1,1).
Sea
 los continuos cambios en los retornos desde el periodo empezado en t-1 hasta t, y P
t
como el precio de los activos financieros al tiempo t; la desagregación de фt se puede escribir de la siguiente manera:
los continuos cambios en los retornos desde el periodo empezado en t-1 hasta t, y P
t
como el precio de los activos financieros al tiempo t; la desagregación de фt se puede escribir de la siguiente manera:
donde p t-1 corresponde a la información en el tiempo propuesto menos una unidad y ε t los errores de dicha desagregación considerados como valores no predictivos; el valor esperado para el i-ésimo proceso de autorregresión se escribe como:
Los valores no predictivos se pueden escribir como procesos de tipo ARCH ε t = m t σ t donde corresponde a un vector de medias de 0, varianza 1 y la varianza condicional de ε t es (Timotheos, Alexandros y Starvos, 2003).
Con lo anterior, la varianza condicional del modelo ARCH(q) se escribe como:
donde ) c i ≥ 0 ∀i = 1, … ,q y corresponde a la reacción a los nuevos comportamientos en el mercado; a través de la anterior definición se logra generalizar el modelo ARCH convirtiéndolo en un Garch(p,q) con la siguiente varianza condicional:
donde si c + β < 1, el proceso se considerara estacionario. Y, a su vez, βi. sostiene la persistencia de la heterocedasticidad en el tiempo. Para el caso del modelo Garch (1,1), la varianza condicional se escribe de la siguiente manera:
El modelo GARCH(p,q) propone una solución bastante buena frente a problemas con la volatilidad y las colas pesadas de la distribución de los retornos, por lo que genera estimaciones confiables al influir este factor difícil de modelar y pronosticar.
Por otro lado, este modelo carece de eficiencia, por las limitaciones que posee en cuanto a la varianza dependiente de la magnitud y no de los e , lo que no es evidente en el comportamiento de los precios donde se encuentra un factor de apalancamiento, pues los activos presentan correlaciones negativas entre ellos y en repercusión logran cambios en la volatilidad (Angelidis et al., 2003).
En respuesta a estas limitaciones impuestas por el modelo de tipo Garch, surge el uso de este mismo a manera exponencial EGARCH(p,q), el cual cuenta con la siguiente forma:
donde λ t . corresponde a un factor asimétrico.
En la estimación de los parámetros de los modelos ARCH se usa comúnmente máxima verosimilitud asumiendo que la porción estocástica m t de los errores son independientes e idénticamente distribuidos y el seguimiento del supuesto de densidad para estos d(mt; v); con lo anterior, la función de log-verosimilitud para el parámetro 0 en una muestra de n observaciones se escribe de la siguiente manera:
Donde In (L(θ)) cambia dependiendo de la función de densidad asumida sobre la porción estocástica m t .
Siguiendo desarrollo del trabajo, se calcula la varianza condicional para el modelo Garch(p,q) en el tiempo t + 1 como:
Una vez obtenida la anterior varianza condicional, existe entonces una distribución a seguir de manera que se procede a retroceder y calcular el VaR en el periodo t+1 a un cuantil específico multiplicándolo por la varianza condicional así:
donde (1 - α) varía dependiendo de la distribución supuesta para los errores.
Cabe resaltar que el modelo EWMA es un caso especial del modelo Garch (1,1) donde reemplazando en la fórmula original p=1, q=1, a=0 y (c0 + β)=1, resulta en la ecuación planteada anteriormente (27).
5. BACKTESTING
La gran cantidad de métodos para estimar el VaR es una razón significativa de por qué se debe verificar su desempeño y cuál es la metodología que realmente está reflejando el comportamiento del mercado. El backtesting es un procedimiento estadístico donde las pérdidas y ganancias son comparadas correspondientemente al valor en riesgo estimado.
La investigación hecha por los bancos para medir la fiabilidad de los métodos de estimación del VaR utilizando pruebas retrospectivas se divide en las siguientes tres categorías:
Test de cobertura: Estos evalúan si la frecuencia con la que se dan excepciones donde el modelo propuesto por el VaR no captura con precisión los cambios en la volatilidad y correlación del mercado, son consistentes con el cuantil de pérdida que la medida de riesgo trató de reflejar.
Test de distribución: Estos proponen pruebas de bondad y ajuste para las distribuciones de pérdida pronosticadas por la medida de riesgo.
Test de independencia: Estos buscan determinar si hay independencia entre periodos elegidos.
Test de cobertura: Este test se basa en ver el número de excepciones diarias en el que las pérdidas generadas por el portafolio superan los valores estimados por cada VaR, por lo que si el número de excepciones es menor a un nivel de confianza seleccionado, el modelo sobreestima el riesgo; por otro lado, si el número de excepciones es mayor, hay un factor de subestimación en el riesgo.
Sea Q el cuantil de pérdidas asociadas al portafolio; el proceso que implica el exceso de las pérdidas se escribe de la siguiente manera:
donde I t es idénticamente distribuida e independiente. Se define la cobertura z como la frecuencia de veces que se excede el VaR como:
Sea Y el número de excedentes como
 donde d corresponde a los datos históricos siendo estos realizaciones de It.Y Y una variable aleatoria con distribución binomial con parámetros (q + 1, 1 - z).
donde d corresponde a los datos históricos siendo estos realizaciones de It.Y Y una variable aleatoria con distribución binomial con parámetros (q + 1, 1 - z).
Al aumentar el número de excedentes se puede aproximar esta distribución binomial a una normal estándar:
donde pt es el número esperado de excedentes y p (1- p)t su varianza.
Para el criterio de rechazo si se toma la hipótesis nula como cierta a un nivel a* de significancia dado, se deben encontrar los valores y1 y y2 de tal forma que P(Y ∉ [y 1,y 2]) < α*. Siguiendo a esto, se establece un criterio para varios intervalos de [y1,y2] de tal manera que al observar el VaR en el periodo t + 1 y a un número de excedentes si Y ∉ [ y 1 , y 2 ], se rechaza la estimación del VaR.
■ Test de cobertura de Kupiec
Este es uno de los test más conocidos con respecto a las tasas de fracaso, pues este intenta describir si el número de excepciones o excedentes es consistente con el nivel de confianza especificado; el test indica que, bajo la siguiente hipótesis nula, el número de excepciones o excedentes sigue una distribución binomial igual a la del test de cobertura.
donde x son las excepciones y n corresponde al número de observaciones; por medio de lo anterior se determinan las diferencias significativas de la tasa de fracaso p con respecto a p. Bajo el test de máxima verosimilitud, el estadístico de prueba presenta la siguiente forma:
donde bajo la hipótesis nula L(TF)~X 2 (1) , se tiene que si este estadístico excede X 2 (1), la hipótesis nula se rechaza y el modelo de estimación para el VaR es ineficiente.
■ Test TUFF de Kupiec
Este test parte de supuestos iguales a los del test anterior; la diferencia se evidencia en la probabilidad de cada excepción, siendo cada una de estas la inversa del nivel de confianza del VaR. Para este test, bajo máxima verosimilitud el estadístico de prueba es el siguiente:
donde v representa el tiempo que se toma hasta que ocurre la primera excepción en la muestra y el estadístico L(TUFF)~ X 2 (1), por lo que si el estadístico es menor al valor crítico, el modelo de estimación es aceptado.
6. ANÁLISIS DESCRIPTIVO A NIVEL ESTADÍSTICO DEL MERCADO DE DEUDA PÚBLICA
6.1 Introducción a los modelos Arima
Se entiende por modelos Arima, aquellos que se caracterizan por ser autorregresivos integrados de media móvil; de igual manera según Castaño, la propiedad de memoria larga en una serie de tiempo suele entenderse como la persistencia que muestran las autocorrelaciones muestrales de ciertas series de tiempo estacionarias, las cuales decrecen a un ritmo muy lento, pero finalmente convergen hacia cero (Castaño, Gómez y Gallón, 2008; Lemus y Castaño, 2013).
El comportamiento citado, según Beran (1994), no es compatible con la función de auto-correlación (acf) de los procesos estacionarios autorregresivos y de medias móviles ARMA (p, q), que imponen un decrecimiento exponencial en las autocorrelaciones, ni con el decrecimiento casi nulo de los modelos integrados no estacionarios ARIMA (p, d, q).
■ Modelos Arima (p, q, d).
Según Brockwell (2006), un proceso estocástico {Zt; є G Z} sigue un proceso autorre-gresivo integrado de media móvil Arima (p, d, q) si es una solución a la ecuación:
donde ϕp (B) es el polinomio autorregresivo estacionario de orden p y θq (B) es el polinomio de media movil invertible de orden q, ambos en terminos del operador de rezagos B y, ademas, no tienen raices comunes entre si. Si d = 0, el proceso en la ecuacion (46) corresponde a un proceso ARMA (p, q) estacionario e invertible; en este caso, θ0 esta relacionado con la medida del proceso. Si d ∈ Z+, el proceso en la ecuación (46) corresponde a un proceso no estacionario homogeneo de raices unitarias; en este caso, θ0 es llamado el termino de tendencia deterministica del proceso. El proceso (at) es una sucesion de variables aleatorias no observables, con media cero y varianza finita σ 2 a .
6.2 Pruebas de raíz unitaria
■ Prueba de Dickey-Füller aumentada
En la práctica, no siempre es posible representar una serie de tiempo empleando alguno de los modelos donde no hay correlación serial en el término de error. En este caso, Dickey y Füller proponen extender la prueba considerando los siguientes modelos:
Modelo I:
Modelo II:
Modelo III:
donde at es un ruido blanco gaussiano de media cero y varianza constante. Con la finalidad de probar la existencia de una raíz unitaria, se deben contrastar las siguientes hipótesis según el modelo considerado en el estudio:
H0: y = 0. Bajo esta hipótesis, la serie tiene raíz unitaria, lo que implica que el proceso no es estacionario.
Ha: y < 0. Bajo esta hipótesis, la serie no tiene raíz unitaria y, por lo tanto, la serie es estacionaria.
El estadístico de prueba para cada una de las pruebas es
donde y es el estimador por mínimos cuadrados de y se(y) es el error estándar en el modelo bajo estudio. La distribución de tbajo la hipótesis nula no es la t- student tradicional, sino que pertenece a una clase de distribuciones no estándar y se encuentra tabulada para diferentes valores de n y niveles de significancia α (Dickey y Füller, 1979). Si t (α, n) es el percentil que acumula una probabilidad inferior de α de dicha distribución, se rechaza la hipótesis nula si el valor observado t es menor que t (α, n).
■ Prueba de Phillips-Perron
En Phillips y Perron (1988) se propone una modificación de la prueba de Dickey-Füller que difiere de esta en cómo tratar la correlación serial y la heterocedasticidad en los errores. Para implementar esta prueba se considera uno de los siguientes modelos:
Modelo I:
Modelo II:
Modelo III:
donde ut es un proceso sin raíz unitaria 7(0) y puede ser heterocedástico. La prueba de Phillips-Perron (P-P) realiza una corrección no paramétrica de la correlación y la heterocedasticidad presentes en el término de error ut de los modelos enunciados. Los estadísticos de prueba son:
Bajo la hipótesis nula, H0: y = 0 (equivalente α p = 1), los estadísticos de prueba de Phillips-Perron, Zp y Zt tienen la misma distribución asintótica que el estadístico de prueba de la prueba de Dickey-Fuller aumentada y sesgo estadístico normalizado.
■ Introducción a los modelos Garch
Los modelos autorregresivos condicionalmente heterocedásticos (ARCH) fueron introducidos por Bollerslev (1986), y su generalización (Garch) se introdujo por primera vez en Engle (1982). En estos modelos, el concepto clave es la varianza condicional, esto es, la varianza condicional en el pasado. En los modelos Garch clásicos, la varianza condicional se puede expresar como una función lineal de los valores pasados al cuadrado de la serie. Esta especificación particular es capaz de capturar los principales hechos estilizados que caracterizan las series financieras. La estructura "lineal" de estos modelos se puede visualizar a través de varias representaciones que serán revisadas a continuación
La definición de un modelo Garch vendría dada por:
Un proceso (єt) es llamado un proceso Garch (p, q) si sus primeros dos momentos condicionales existen y satisfacen lo siguiente:
Existen constantes ω, al, . . ., αq y β1, . . ., βp tal que
La ecuación (46) se podría escribir en forma más compacta como:
donde B es el operador de rezagos y α, β fi son polinomios de grado q y p respectivamente. Si β= 0, tenemos que
y este proceso se denomina ARCH(q). Por definición, la innovación del proceso є 2 t es la variable v t = є 2 t + σ 2 1
sustituyendo en la ecuación anterior las variables σ 2 . por є 2 t-i - v t , se obtiene la siguiente representación:
donde r = máx (p, q). Esta ecuación tiene la estructura lineal de un modelo Arima, lo que permite un cálculo sencillo en las predicciones lineales. Hay una prueba que detecta la presencia de heterocedasticidad condicional que fue introducida por Mcleod que no es más que el estadístico de Ljung-Box para la serie al cuadrado o los residuales al cuadrado de un modelo Arima (Mc Leod, 1983).
Los modelos Garch (p, q) capturan de forma adecuada varias características de las series de tiempo financieras, como el agrupamiento de la volatilidad.
Por otro lado, la estructura Garch presenta algunos inconvenientes de aplicación ya que la variación depende solo de la magnitud y no del signo de εt, que es algo que no es adecuado en el comportamiento empírico del mercado de valores, donde un efecto de apalancamiento puede estar presente.
Los estimadores de máxima verosimilitud de los parámetros se obtienen mediante el algoritmo de maximización numérico propuesto por Marquardt (1963), aunque Bollerslev (1986) y Wooldridge proponen un estimador usando la función de quasiverosimilitud que resulta tener una distribución asintóticamente normal y proporciona errores estándar asintóticos que son válidos cuando no hay presencia de normalidad.
En resumen, la predicción de la varianza condicional un paso adelante para el modelo Garch (p, q) es
Por lo tanto, es sencillo calcular la predicción un paso adelante del VaR bajo todos los supuestos distribucionales y para observaciones con media cero como:
donde F(α) corresponde al cuantil (95 % o 99 %) de la distribución asumida y σ" t+1 | t corresponde a la predicción de la desviación estándar condicional en el tiempo t + 1 dada la información hasta el tiempo t.
■ Estimación del valor en riesgo en tes tasa fija
Para efectos de determinar el valor en riesgo del mercado de deuda pública, se tomaron los títulos más negociado en el mercado de renta fija: los TES tasa fija de fecha de vencimiento 24 de julio de 2020 y los TES de fecha de vencimiento 24 de julio de 2024. En el proceso de estimación del valor en riesgo se homologaron las series cuyo periodo inició desde el 9 de enero de 2014 al 23 de junio de 20165.
■ TES tasa fija de fecha de vencimiento 24 de julio de 2020
A continuación, se presenta un pantallazo de la plataforma Bloomberg, en donde se describe las características faciales de la referencia TES tasa fija de fecha de vencimiento 24 de julio de 2020.

Figura 6 Pantallazo de la plataforma Bloomberg TES tasa fija de fecha de vencimiento 24 de julio de 2020
Como se puede apreciar en el pantallazo de la plataforma Bloomberg, la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020 cuenta con una tasa cupón del 11 %, y fue considerado por los inversionistas como el activo refugio en el mercado local; cuenta adicionalmente con una calificación en su emisión por parte de las agencias calificadoras de riesgo S&P y Fitch de BBB.
A continuación, se muestra el comportamiento de la referencia diariamente durante el periodo 2014 a 2016:

Figura 7 Comportamiento del precio de la referencia TES tasa fija de fecha de vencimiento 24 de julio de 2020
En el proceso bajo estudio, no se observa ninguna tendencia determinística evidente en la serie. Por otra parte, la varianza incondicional del TES de fecha de vencimiento 24 de julio de 2020 parece cambiar según el nivel del proceso, lo que posiblemente indica que se deba realizar una transformación de potencia que permita estabilizar la varianza mencionada. Se identificó la transformación de Box-Cox más adecuada para estabilizar la varianza incondicional del proceso, pero al obtener valores A demasiado grandes o pequeños durante la optimización, esto puede indicar que la transformación es de poca utilidad para el tipo de serie usada; por lo tanto, se toma la decision de no transformarla.
En el análisis de la serie del TES de la referencia de fecha de vencimiento 24 de julio de 2020, se determinará si el grado de interdependencia muestral del proceso corresponde al de un proceso estacionario o al de un proceso no estacionario homogéneo empleando diferentes pruebas de raíz unitaria siguiendo la metodología de Box-Jenkins (2008), para la construcción de modelos en series de tiempo univariadas.
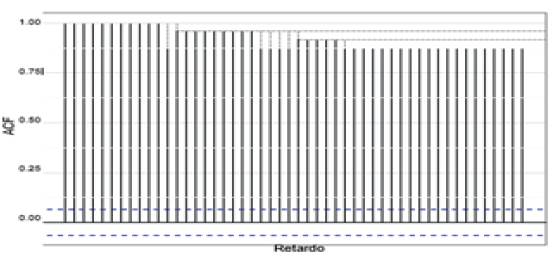
De acuerdo con la figura 8, se presenta la función de autocorrelación, la cual muestra un decaimiento lento, comportamiento característico de los modelos Arima (p, d, q).
En la figura 9, se evidencian 4 instancias o puntos los cuales hicieron que el TES tuviese un comportamiento bajista como consecuencia del apetito de los inversionistas hacia la parte media de la curva, producto del desestímulo en el mercado financiero local hacia la renta variable causado u originado principalmente por la caída de los precios del petróleo, que fijaron por debajo de los USD 45 el valor del barril de crudo.
■ Resultados de las pruebas de raíz unitaria en el TES de la referencia de fecha de vencimiento 24 de julio de 2020
Al implementar la prueba ADF se consideró inicialmente la existencia de tendencia determinística y deriva. En la tabla 2 se presentan los resultados obtenidos para esta prueba, incluyendo un número máximo de retardos igual a la raíz cubica de la longitud de la serie.
Tabla 2. Resultados prueba ADf-Modelo 3 para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020
En la tabla 3, se presentan los resultados de regresión ajustada en este caso:
Tabla 3. Regresión ajustada prueba ADF-modelo 3 para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020
Se puede observar que el rezago de la prueba ADF no resulta estadísticamente significativo, y lo mismo se puede concluir con respecto a la tendencia determinística. Dado que la prueba anterior puede estar sobreparametrizada al incluir la tendencia determinística, se específica nuevamente la prueba ADF empleando el modelo 2, así como la inclusión de un número de retardos igual a la raíz cúbica de la longitud de la serie.
Tabla 4. Resultados prueba ADF-modelo 2 para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020
De las tablas 3 y 4 se concluye que hay evidencia suficiente para no rechazar la hipótesis nula de raíz unitaria, ya que en ambas pruebas el estadístico es menor que el percentil a (nivel de significancia), por lo que se concluye que hay raíz unitaria en la serie de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020.
■ Procedimiento de identificación y estimación del valor en riesgo VaR en el TES tasa fija de fecha de vencimiento 24 de julio de 2020
A continuación, se ilustra la implementación del procedimiento propuesto por Box Box, Jenkins y Reinsel (2008) para la identificación y estimación de un modelo adecuado para la referencia del TES de fecha de vencimiento 24 de julio de 2020. Primero se evalúa la fluctuación empírica de la serie original; en la figura 10 se puede observar que a un nivel de significancia del 5 % se rechaza la hipótesis nula en la que se supone que no hay cambios estructurales en el proceso.
Después de esta medición se ajusta el modelo usando el criterio AIC, donde se obtiene un modelo Arima (0,1,1), cuya ecuación estimada viene dada por:
Considerando un nivel de significancia del 5 %, se puede concluir que la estimación del coeficiente del modelo de corto plazo del proceso en el modelo completo es significativa. A continuación, se presenta el resultado de la prueba de Ljung-Box para los residuales del modelo identificado.
Los resultados obtenidos en la tabla 5 permiten concluir que no hay correlación serial en los residuales del modelo identificado. Lo anterior indica que el modelo es adecuado para capturar la correlación serial a corto plazo presente en la serie diferenciada. Después se evalúa la posibilidad de un efecto autorregresivo condicionalmente heterocedástico, por medio de la prueba ARCH-LM a la serie original. En la tabla No 6 se muestra que sí hay un efecto significativo de la heterocedasticidad condicional.
Tabla 5 Prueba de Ljung-Box para los residuales del modelo identificado de la serie de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020

Tabla 6 Prueba de ARCH-LM para la serie de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020

En la figura 11, se muestra el autocorrelograma (simple y parcial) de las series de los residuales al cuadrado.
Figura 11. Correlograma de la serie de los residuales estandarizados al cuadrado de la referencia del TES de fecha de vencimiento 24 de julio de 2020
En la figura 12 se muestra la fluctuación empírica para los residuos del modelo, donde se puede observar que no se rechaza la hipótesis de estabilidad estructural de la serie
Figura 12. Fluctuación empírica de los residuos de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2020
Usando los rezagos que salen de la banda azul del correlograma, se procede a evaluar por medio del AIC el mejor modelo Garch, donde se obtiene un Garch (0,7), se crean las bandas de confianza y se obtiene la figura 13.

Figura 13 Bandas de confianza efecto Garch de la serie de la referencia del TES de fecha de vencimiento 24 de julio de 2020
A continuación, se muestra la comparación de las metodologías del VaR para la referencia del TES de tasa fija de fecha de vencimiento 24 de julio de 2020:
Tabla 7 Análisis comparativo de las metodologías de estimación del valor del valor en riesgo VAR para la referencia del TES de tasa fija de fecha de vencimiento 24 de julio de 2020

De la anterior tabla podemos afirmar que con un nivel de significancia del 5 %, ninguna metodología logra estimar de forma adecuada el valor en riesgo, pero definitivamente la aproximación dada por el modelo GARCH resulta ser el mejor modelo.
■ TES tasa fija de fecha de vencimiento 24 de julio de 2024
A continuación, se muestra un pantallazo de la plataforma Bloomberg en donde se describe las características faciales de la referencia fecha de vencimiento 24 de julio de 2024:

Figura 14 Pantallazo de la plataforma Bloomberg TES tasa fija de fecha de vencimiento 24 de julio de 2024
Como se puede apreciar en el pantallazo de la plataforma Bloomberg, la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024 cuenta con una tasa cupón del 10 %, y que fue considerado por los inversionistas como el activo refugio en el mercado local; cuenta adicionalmente con una calificación en su emisión por parte de las agencias calificadoras de riesgo S&P y Fitch de BBB.
A continuación, se muestra el comportamiento de la referencia diariamente durante el periodo 2014 a 2016:
Figura 15. Comportamiento histórico de los precios de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024
Como se puede visualizar, el comportamiento descrito en el periodo 2014-2016 obedeció principalmente a la demanda por parte de los inversionistas de la parte corta de la curva, dada la incertidumbre generada en el mercado ante la caída de los precios del barril de petróleo, que puso en duda la capacidad del gobierno de disminuir sus acreencias en el largo plazo y la posibilidad de un mayor nivel de endeudamiento ante la caída de la renta petrolera.
En el proceso bajo estudio no se observa ninguna tendencia determinística evidente en la serie del TES tasa fija de fecha de vencimiento 24 de julio de 2024. Por otra parte, la varianza incondicional de la serie parece cambiar según el nivel del proceso, lo que posiblemente indica que se deba realizar una transformación de potencia que permita estabilizar la varianza mencionada. Se identificó la transformación de Box-Cox más adecuada para estabilizar la varianza incondicional del proceso, pero al obtener valores A demasiado grandes o pequeños durante la optimización, esto puede indicar que la transformación es de poca utilidad para el tipo de serie usada. Así que se decide no transformar la serie.
En la figura 16 se presenta la función de autocorrelación de la serie; aquí se observa un decaimiento lento, comportamiento característico de los modelos ARIMA (p, d, q). A continuación, se determinará si el grado de interdependencia muestra del proceso corresponde al de un proceso estacionario o al de un proceso no estacionario homogéneo, según se emplean diferentes pruebas de raíz unitaria que siguen la metodología de Box-Jenkins para la construcción de modelos en series de tiempo univariadas.
A continuación, se muestra en la figura 17 la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024 con puntos de quiebre:
Los puntos de quiebre han estado relacionados con la publicación de fundamentales de la economía nacional en donde la caída de los precios del petróleo ha disminuido la capacidad del Gobierno nacional para afrontrar sus gastos, lo que provocó un desgano en el mercado de renta fija ante la amenaza de menores ingresos fiscales durante el periodo 2014-2016, con la consiguiente depreciación del peso colombiano frente a la divisa.
■ Resultados de las pruebas de raíz unitaria en el TES de la referencia de fecha de vencimiento 24 de julio de 2024:
Al implementar la prueba ADF se consideró inicialmente la existencia de tendencia determinística y deriva. En la tabla 8 se presentan los resultados obtenidos para esta prueba incluyendo un número máximo de retardos igual a la raíz cúbica de la longitud de la serie.
Tabla 8 Resultados prueba ADF-modelo 3 para la referencia del TES de fecha de vencimiento 24 de julio de 2024

En la tabla 9, se presentan los resultados de la regresión ajustada en este caso:
Tabla 9 Regresión ajustada prueba ADF modelo 3 para la referencia del TES de fecha de vencimiento 24 de julio de 2024

Se puede observar que el primer rezago de la prueba ADF no resulta estadísticamente significativo, e igual cconclusión se puede dar sobre la tendencia determinística. Considerando que la prueba anterior puede estar sobreparametrizada al incluir la tendencia determinística, se especifica nuevamente la prueba ADF empleando el modelo 2, y se incluye un número de retardos igual a la raíz cúbica de la longitud de la serie. En la tabla 10 se presentan los resultados obtenidos:
Tabla 10 Resultados prueba ADF-modelo 2 para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024

De las tablas 7 y 9 se concluye que hay evidencia suficiente para no rechazar la hipótesis nula de raíz unitaria, ya que en ambas pruebas el estadístico es menor que el percentil α (nivel de significancia), por lo que se concluye que hay raíz unitaria en la serie de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024.
■ Procedimiento de identificación y estimación del valor en riesgo VaR en el TES tasa fija de fecha de vencimiento 24 de julio de 2024
A continuación, se ilustra la implementación del procedimiento para la identificación y estimación de un modelo adecuado para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024. Primero se evalúa la fluctuación empírica de la serie original; en la figura 18 se puede observar que ante un nivel de significancia del 5 %, se rechaza la hipótesis nula en la que se supone que no hay cambios estructurales en el proceso:

Figura 18 Fluctuación empírica para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024
Usando el criterio AIC, seguidamente se ajusta el mejor model; así se obtiene el siguiente modelo Arima (1, 1, 2), cuya ecuación estimada viene dada por:
Considerando un nivel de significancia del 5 %, se puede concluir que la estimación del coeficiente del modelo de corto plazo del proceso en el modelo completo es significativa. A continuación, se presenta el resultado de la prueba de Ljung-Box para los residuos del modelo identificado.
Tabla 11 Prueba Ljung-Box para los resultados del modelo identificado para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024

Los resultados obtenidos en la tabla 11, permiten concluir que no hay correlación serial en los residuales del modelo identificado.
Lo anterior indica que el modelo es adecuado para capturar la correlación serial a corto plazo presente en la serie diferenciada.
Después se evalúa la posibilidad de un efecto autorregresivo condicionalmente heterocedástico por medio de la prueba ARCH-LM a la serie original.
Tabla 12 Prueba de ARCH-LM para la serie para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024

A continuación, se muestra la comparación de las metodologías del VaR para la referencia de fecha del TES tasa fija de fecha de vencimiento 24 de julio de 2024
Tabla 13 Análisis comparativo de las metodologías de la estimación del VAR para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024

De la anterior tabla se puede afirmar que dado un nivel de significancia del 5 % ninguna metodología logra estimar de forma adecuada el valor en riesgo VaR; sin embargo, los modelos GARCH resultan ser los que mejor explican la variabilidad de las series analizadas, y por esta razón se les considera como la mejor alternativa.
A continuación, se muestra el correlograma de la serie de los residuales para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024:
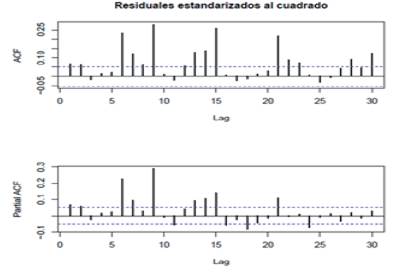
Figura 19 Correlograma de la serie de los residuales al cuadrado para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024
Por otro lado, a continuación, se muestran las bandas de confianza del efecto Garch para la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024:
Según se puede ver en la figura 20, el modelo Garch es el que mejor explicita el comportamiento del TES tasa fija de la referencia de fecha de vencimiento 24 de julio de 2024.

Figura 20 Bandas de confianza efecto Garch de la referencia del TES tasa fija de fecha de vencimiento 24 de julio de 2024
A continuación se muestra en la figura 21 la fluctuación empírica para los residuales del modelo, donde se puede ver que no se rechaza la hipótesis de estabilidad estructural de la serie.
7. conclusiones
Los métodos para el cálculo del VaR son usualmente divididos en métodos paramétricos, no paramétricos e incluso semiparamétricos. Los modelos paramétricos están basados en los parámetros de la distribución de los factores de riesgo, mientras que los no paramétricos son modelos de simulación o históricos. Hay varios métodos para el cálculo de este indicador, donde el supuesto de normalidad en la mayoría de los casos es el más importante y el más ideal para las carteras simples.
Cuando se implementa la metodología de VaR histórico, el primer paso es el de identificar los instrumentos en el portafolio para obtener las series de tiempo durante un periodo de tiempo definido; luego se utilizan las ponderaciones del portafolio para simular retornos hipotéticos que se habrían realizado, suponiendo que la cartera actual se ha mantenido durante el periodo de observación. Esto es una desventaja, ya que el mercado es bastante volátil, por lo que resulta con desventajas a la hora de implementar esta metodología.
Con la metodología EQWT, el cálculo del VaR resulta ser bastante sencillo, siempre que se mantenga el supuesto de normalidad, ya que las propiedades matemáticas de la distribución normal estándar permiten una trazabilidad fácil entre diferentes niveles de confianza y periodos de espera.
En general, el supuesto de normalidad es bastante fuerte y hay que validarlo para aplicar de forma adecuada esta metodología, pero, en general, en las series financieras este supuesto es bastante escaso sin el ajuste de la serie de tiempo.
En este trabajo se ha mostrado que los retornos no tienen distribución normal, dadas las pruebas de bondad de ajuste implementadas. Además, la presencia de correlación de estos determina la presencia de un fenómeno de "ruido negro" en la función de autocorrelación.
Adicionalmente, el supuesto de varianza constante tampoco se puede validar. Con base en todo lo anterior, es muy difícil crear un intervalo de confianza que tenga la menor pérdida posible o, de otra forma, estimar el máximo del x % de los retornos mínimos. Por consiguiente, para la estimación del VaR es más adecuado hacer una predicción de la volatilidad, lo cual es posible mediante los modelos Garch, ya que esta es la aproximación más adecuada para la estimación.
Finalmente, se hace necesario implementar en futuras investigaciones metodologías no paramétricas dado que las paramétricas no permitieron escoger cuál es la metodología que mejor explica el comportamiento del valor en riesgo en el mercado de deuda pública. Sin embargo, al realizar el backtesting se encontró que los modelos Garch son los que presentan una mejor predicción de la volatilidad
Otra alternativa que puede presentarse en nuevas investigaciones es el cálculo del VaR si se usan distintas distribuciones en vez del supuesto de normalidad. Una de las maneras más eficientes puede ser también el uso de metodologías que incluyan no solamente componentes heterocedásticos, como los son Garch, sino modelos de dependencia continua como cópulas o vinecópulas, debido a que estos logran capturar la dependencia no lineal sobre los distintos activos en un portafolio.