Introduction
Mastering of mathematical skills is required in various everyday activities and the ability to solve operations is a prerequisite for performance in other mathematical skills, like fractions, ratios, division, and decimals. Despite the importance of this numerical repertoire, studies conducted in different countries indicate that multiplicative facts still represent a learning challenge for primary school children (Fauzan & Arini, 2019; Park & Nunes, 2001). In 2012, the United Nations Educational, Scientific and Cultural Organization (UNESCO) disclosed the global challenges for mathematics education, highlighting the need to ensure the meaningful learning of fundamental mathematics repertoires, among them multiplication. This challenge is still a global reality nowadays, as argued by Björklund et al. (2020) when presenting a contemporary overview of general math learning difficulties in children.
The importance of mastering these skills and the Brazilian students’ subpar results in mathematics in national and international reports (Truffi, 2020), have prompted investigations of teaching procedures that can change this reality. Behavior Analysis research, especially those using the stimulus equivalence paradigm, has been developed on different topics in mathematics (Henklain et al., 2017). Some of these researches employed games for teaching (e.g., Gris et al., 2018). Although studies based on the stimulus equivalence paradigm have used games, most examine only additive problems (problems involving addition and subtraction). Thus, research based on the same paradigm using teaching games with multiplication operations remains scarce - prompting further investigation. Developing and evaluating additional tools for teaching Mathematics, such as games, can improve student engagement and, consequently, their performance (Brandão et al., 2019; Rodrigues et al., 2017). Additionally, these tools can also reduce learning problems frequently produced by inadequate teaching plans (Carmo, 2010).
According to the stimulus equivalence paradigm, mathematical behavior involves a network of symbolic relations between stimuli (e.g., dictated numeral, printed numeral, signs, among others), and or between stimuli and responses such as counting, solving operations, and so forth (Prado & de Rose, 1999; Rossit & Goyos, 2009). This model proposes that teaching some relationships can lead to the emergence of others. To teaching and test conditional relations, some studies (Henklain & Carmo, 2013; Rossit & Goyos, 2009) used matching-to-sample procedures. In this procedure, a sample stimulus (e.g., dictated numeral 2) and two or more different comparison stimuli (e.g., printed numerals 2 and 3) are presented successively or simultaneously. Choosing the comparison stimulus previously defined as correct (e.g., printed numeral 2) is differentially reinforced. The Constructed Response Matching-to-Sample (CRMTS) procedure was also employed (Rossit & Goyos, 2009). In this procedure, after presenting a sample stimulus (e.g., a BRL 10 banknote) and comparison stimuli (e.g., 2 BRL banknote), the participants must select the number of banknotes necessary to compose the value that equals the sample stimulus.
In most studies that used these procedures, teaching was done through software or cards (e.g., Henklain & Carmo, 2013; Rossit & Goyos, 2009). Despite the good quality and results obtained by these studies, the use of games to teach mathematical skills is valued in official guidelines (Ministério da Educação do Brasil, 2017) that refer to the teaching of Mathematics. Teaching through games and/or gamified practices can lower student engagement problems1. The games have features that contribute to engagement, such as: increasing levels of difficulty; a demand for learners’ active participation; the presence of clear and defined objectives; an academic content embedded in the narrative; the use of scenarios that reflect real-world experiences; feedback to each action; and learner-paced progress (Perkoski & Souza, 2015). Among the studies that used the stimulus equivalence paradigm to teach mathematical skills with games, those by Godoy et al. (2015), Gris et al. (2018) and Godoy (2018) stand out.
Godoy et al. (2015) evaluated the effects of an adapted domino game to teach money relations to two preschool children. In Step 1, they assessed children’s performances in naming printed numerals, printed values and notes/coins, sets of dots, handling money, and solving addition operations. In Step 2, relations ABBA and ACCA were taught and BCCB was tested, in which A represents printed numerals, B sets of black dots, and C addition operations. In Step 3, ADDA and DEED were taught and DBBD, EBBE, ECCE and DCCD were tested: D represents printed values, and E fictitious banknotes/coins used in the game. The letters represent each set of stimuli. Probe sessions (similar to Step 1) were conducted after Steps 2 and 3. Participants learned all relations taught, demonstrated the emergence of tested relations, showed increased rates of correctly performed operations, and low success rates in handling money.
Considering Godoy’s et al. (2015) findings, especially regarding the resolution of addition operations, Gris et al. (2018) evaluated the effects of teaching conditional relations between numerals (A), sets of dots (B) and addition operations both in digit (C) and scale formats (D). The study used a digital domino game on solving addition operations in both formats called Korsan (Gris & Souza, 2016). Four 7-year-old children participated. All participants showed increased correct responses of solving addition operations. The game proved to be effective and attractive to learners.
As Gris et al. (2018) focused exclusively on addition operations, Godoy (2018) investigated the effects of the same digital domino game on subtraction learning. Three children aged between 5 and 6 took part. The procedures used in both studies were similar, but the latter replaced stimulus classes composed of addition with subtraction operations using digits and scales. Participants showed an increased rate of correct responses when solving subtraction operations. Still, the authors emphasize (as did Gris et al., 2018) the need to include a plot and visual elements in future versions of the game to increase player engagement during matches.
Although these findings show the effectiveness of teaching procedures, such studies only investigated the effect of domino games (analog and digital) in solving additive problems. The guidelines prepared by Brazil’s Ministry of Education (Ministério da Educação do Brasil, 2017) for the National Plan for Literacy at the Right Age (Plano Nacional de Alfabetização na Idade Certa - PNAIC) emphasize the relevance of teaching additive and multiplicative problems for children in first years of elementary school. Schools often teach multiplicative problems after additive ones (Dooren et al., 2010), as multiplication is considered more complex. Also, some aspects of addition are the basis for multiplication, for example, when we add equal parts to solve a multiplication problem. However, multiplying goes beyond adding equal parts. While addition involves joining and separating, multiplication involves three types of situations: (a) one-to-many matching situations; (b) situations involving relationships between variables - covariation; and (c) situations involving sharing and successive splits (Nunes & Bryant, 1996).
One-to-many matching situations are more straightforward and involve proportionality. For example, one bicycle has two wheels; two bicycles have four wheels. The 1:2 ratio and the scalar factor (number of replications) remain constant even when there is variation in pool size. In situations involving relations between variables (covariation), two or more variables change as a function of a convention or causation. For example, if a kilo of rice costs $10, half a kilo costs $5. The price and quantity of rice are connected by a third variable (price per kilo). If weight increases, the price also increases and vice versa, although the price per kilo remains constant. Multiple proportions can be involved, making problems more complex. Finally, situations involving successive distributions and cuts involve the equitable distribution of a set (e.g., x candies divided by y children). According to Nunes and Bryant (1996, p. 150, 152), sharing “consists of establishing a multiplicative relationship between two or more sets…is an action that relates to the operation of division and to the possibility of successive splits”. In these cases, three elements need to be considered: the size of the whole, the number of parts, and the size of parts (Nunes & Bryant, 1996; Starepravo, 2010).
Teaching multiplicative reasoning in elementary school is crucial as it provides students with a foundation for more complex content in high school (Askew, 2018). Although scholars in the field agree that teaching multiplicative problems should not be done exclusively through mechanical operations that do not involve mathematical reasoning (e.g., Parra, 1996; Starepravo, 2010), the role of such processes cannot be ruled out as a learning goal. Computational fluency - i.e., efficient and accurate completion of mathematical operations, which can be enhanced by automatic calculation- can contribute to solving more complex problems, interpreting basic mathematical principles, and allowing greater fluency in solving operations (Burns et al., 2015). All these contributions can lead to greater learner engagement in the discipline. The use of concrete support material is also cited as a facilitator in problem-solving. It favours observation and construction of calculation procedures as well as varied ways of thinking and perceiving reality, allowing mathematical concepts to acquire meaning for learners (Maccarini, 2010). As stated by Pires et al. (2013, p. 91) “it is games, calculators, and all kinds of concrete materials that will make children play and learn at the same time”.
Although digital games have been used to teach mathematical skills, we have not found studies that used games nor the stimulus equivalence paradigm to teach multiplication operations, corroborating the results of Oliveira-Jr et al. (2021). The present study evaluated the effects of an adapted digital domino game based on the stimulus equivalence paradigm to teach relations between numerals, sets of dots and multiplication operations with numbers and scales with the unknowns in varying positions. We used a digital game as a main teaching resource and skewers as hands-on support materials.
The position of the unknowns in operations (for example, x-1=1 being position a; 2-x=1 position b; 2-1=x, position c) and the problem presentation format (digits or scale) can affect the understanding and resolution of problems. Evidence shows that operations with the unknowns in positions a and b are more challenging to solve than those in position c (Hiebert, 1982). As for the presentation format, drawings or graphics can improve children's performance in solving additive problems (Capovilla et al., 1997). Furthermore, pairing digit-to-scale-format operations can lead to the emergence of equivalence classes and improve participants' performances in solving these operations (Gris et al., 2018; Henklain & Carmo, 2013). It is emphasized that the game evaluated in this study was constructed based on the principles and concepts of Behavior Analysis. Skinner (1968, p. 4) writes that "teaching is the act of facilitating learning". Therefore, developing and evaluating a technology that respects the rhythm of the learner, whose complexity of the content gradually increases, that requires the active participation of the learner in the performance of the proposed activities and that does so in a fun way can contribute to free-fears teaching, guilt and anxiety often produced by a practice boring and coercive (Carmo, 2010).
Method
Participants
Two teachers (of 3rd and 4th grades) referred five students aged between 7 and 8 from both sexes with typical development. Table 1 presents de characteristics of the participants. Poor mathematics performance was used as the criterion for the referral. We excluded students referred by their teachers who scored 55% or above in both forms (digits and scales) of multiplication operations at the pretest. All included participants should correctly name numerals and sets of dots from 1 to 15.
Ethical considerations
Participation in the research was voluntary. Parents and the school signed the Informed Consent Term, and the children signed the Assent Term in which they agreed to take voluntarily part of this research. They were also informed that they were free to withdraw from this research at any time. The Ethics Committee for Research with Human Beings at the authors' university approved this research (CAAE: 97002918.7.0000.523).
Location, material, and equipment
Data collection was carried out in a public school in a room assigned by the school’s direction (library, resource room, director’s office, or teachers' room). The rooms were equipped with tables, chairs, books, and or desktop computers. Researchers used a notebook, video camera, tripod, pencil, and paper for data collection and analysis. They also made available six 250 ml plastic cups and 15 black cotton-fiber rods for participants to help solve operations.
Instruments
Researchers used an adapted version of the board game Lince to evaluate participants’ operation resolution skills at the pretest. They used 6x6 cm white cards containing printed numerals 1 to 15 and sets of black dots (1 to 15) for the naming test. Dots on each card were symmetrically distributed. In the intervention stage, we used the game “Korsan: Teaching of Multiplication” in its digital version.
Lince (adapted version for operations using digits and scale format). Lince is a game manufactured by ®GROW. It can be played in figures and in words version. In the original game, the players receive cards with pictures or words printed on it. After a signal, they must find the corresponding figures on the board and cover them with the cards. Whoever does this as quickly as possible wins the game. The game Lince has been adapted by this research group (cf. Godoy, 2018; Gris & Souza, 2016; Gris et al. 2018) to evaluate the children's knowledge in solving arithmetic operations with numbers and in scale format. In this study, the time necessary to find the solution for the operation wasn’t evaluated, only the number of correct matches.
The game contains a pirate-themed board with numerals or sets of dots from 1 to 15, 31 tokens, and 31 cards with multiplication operations using numbers or scales. Unknowns are shown in positions a (10 cards), b (11 cards), and c (10 cards). Figure 1 presents examples of operations in different formats whose results never exceed 15.
Digital game Korsan: Teaching of multiplication (Gris & Souza, 2016). Digital domino game programmed on Unity that teaches conditional relations between numerals (A), set of dots (B), multiplication operations with digits (C) and multiplication operations with scales (D). The game is themed a pirate treasure hunt and contains five stages that allow teaching and testing relations. Participants must help the pirate by solving domino challenges to open the treasure cave. When the pirate arrives at an island, the player must lead him to one of five caves. Each cave has a totem with pre-assembled domino tracks containing three gaps at the top and six moving pieces at the bottom (comparison stimuli).
Each cave contains a new set to either teach or test a relation. To advance from one cave to the other, players must correctly match all domino faces considering both tile sides. In the teaching phases, correct moves consist of selecting pieces and completing gaps in the track. After completing all gaps, a blue light indicates that they were correctly fitted and are not replaced by a new comparison stimulus.
In incorrect moves, pieces selected by participants complete gaps in the track. When completing all gaps, a yellow light indicates that one of them was incorrectly placed. In this case, a correction procedure is performed, which involves repeating the cave. When the piece from an incorrect trial is now paired correctly, a crab moves across the screen and steals the piece, requiring participants to repeat the trial again. In test phases of conditional relations, no specific consequences are programmed for trials. Instructions are presented on the computer screen and must be read by either the participant or researcher. Figure 2 illustrates some game screens as participants view them.
Procedure
The experiment was sorted into eight stages (in that order): Pretest, Teaching 1 (ABBA, ACCA), Test 1 (BCCB), Teaching 2 (CDDC), Test 2 (BDDB, ADDA), Posttest and Follow-up. Participants performed all sessions individually across all stages - filmed for later data recording - and had free access to the cups and rods.
Pretest, Posttest and Follow-up. We adopted similar structures for naming numerals and sets of dots, and solving multiplication operations with digits and scales varying positions of unknowns. Participants received cards with numerals and sets of dots from 1 to 15 and were asked to say the written number-word or the quantity of dots printed on the card. For multiplication operations, we used the adapted version of Lince. Participants received cards with multiplication operations, namely 31 cards with digits and 28 with scales (depending on the target skill). The task consisted of drawing a card from the pile, solving the operation, and locating the answer on the board by covering it with a token. We first tested operations with figures then with scales. Specific consequences did not follow responses.
Teaching and testing conditional relations. Here we taught relations between numerals and sets of dots (ABBA), numerals and multiplication operations (ACCA), and multiplication operations with digits and scales (CDDC). In test phases, we tested the emergence of relations between sets of dots and multiplication with digits (BCCB), sets of dots and multiplication with scales (BDDB), and numbers and multiplication with scales (ADDA). To advance through the game phases, participants needed 80% unaided correct responses while solving operations. In phases with multiplication operations (C and D), the unknowns were presented first in position c, then b, and finally a. After that, the position of unknowns varied at random.
In test phases, a message on the game informed participants they would not receive feedback on their performance, and they could not request assistance while solving operations. After completing all activities presented in that phase, a new cave was opened. Researchers assisted in all phases while handling the mouse, dragging pieces, and clicking on the icons whenever necessary. After the last game phase (ADDA test), posttest was carried out. P3 (Participant 3), P4 and P5 also performed a follow-up session 45, 41 and 38 days after the end of the intervention, respectively. Time lapsed until follow-up varied due to school holidays and activities that could not be interrupted. P1 and P2 could not undergo follow-up due to the proximity to school holidays.
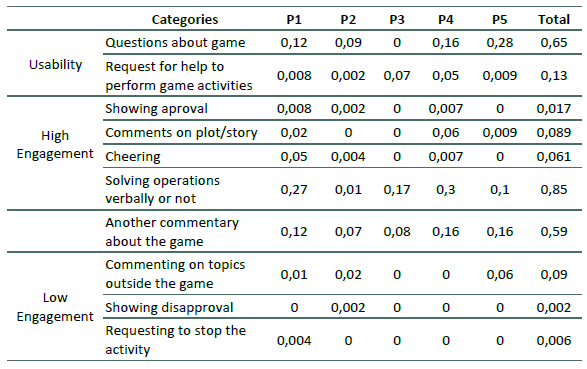
Usability and engagement assessment. We used a categorized record of in-session behaviors (adapted from Gris & Souza, 2016) to assess usability and participant engagement. Usability categories were: asking questions about the game, requesting help to perform game activities and using rods to perform operations. Participant engagement was assessed in terms of high and low engagement. High engagement categories were: showing approval, commenting on the plot/story, cheering, solving operations verbally (e.g., counting using fingers or rods) and another commentary about the game (e.g., naming the numbers presented on computers’ screen, talking about how to solve an operation, and others). Low engagement categories were: showing disapproval, commenting on topics outside the game and requesting to stop the activity.
Aid levels. Aid levels were sorted into: independent (child performed all tasks without help), supervision (researcher verbally instructs child on what to do); minimal assistance (researcher verbally instructs child on what to do, assists the use of rods to solve operations, points to the computer screen indicating what to do, helps to use the mouse to guide the avatar); and moderate assistance (all in minimal assistance plus researcher explains algorithm to perform operations before the child plays or and asks, and helps participants to use rods to perform the operations).
Interobserver agreement. The recorded sessions were transcribed and analyzed by two researchers who recorded the number of times they observed the occurrence of the categories referring to usability, engagement, and levels of assistance. Then, the records were compared by calculating the percentage of agreement between them (agreement/agreement+disagreementox100). The data indicated agreement above 80% for the categories referring to usability and engagement (82.5% for usability, 93.6% for engagement). For the levels of assistance, the percentage of agreement was above 90%.
Results
Except for P4, all participants named numerals and sets of dots with 100% accuracy at the pretest - the participant said “12” when shown a 13-sets of points. As for solving operations with numbers, except for P4 (61.2% correct responses on average - 50% with the unknown in position a, 63.3% in position b, and 70% in position c), all participants performed below 55%. Regarding operations with scales, only P5 performed above 55% (68.1% on average - 60% with unknown in position a, 55.5% in position b, and 88.8% in position c). Figure 3 shows participants’ performances at the pretest, posttest, and follow-up.
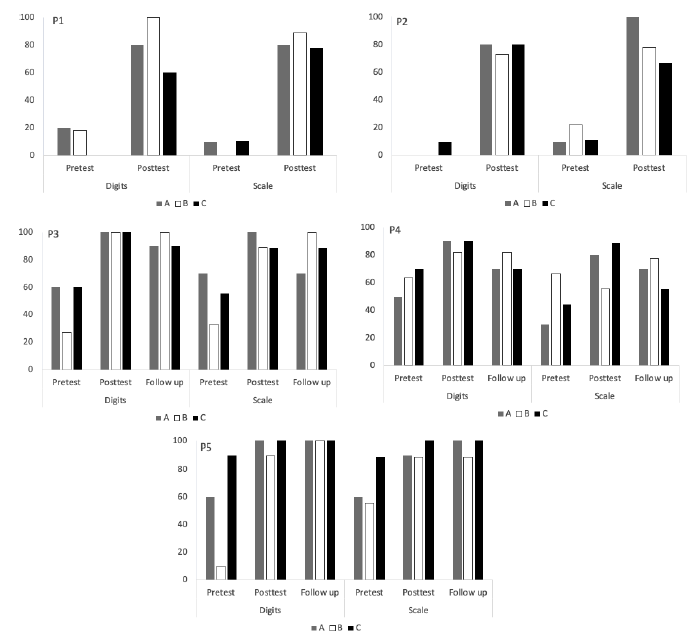
Figure 3. Percentage of correct responses at Pretest, Posttest and Follow-up for each participant in operations with numbers and scales considering the position of the unknowns (a, b and c).
In the teaching phases, P1 and P4 underwent five sessions, P2 nine, P3 three, and P5 four. Each session lasted about 30 minutes. In some cases, participants required more than one session (e.g., seven ACCA sessions for P2) to complete cave tasks. Regarding tests, except for P1 and P2, who required two and eight BCCB sessions respectively, and P2, who needed two sessions to complete DBBD and ADDA, all were carried out in one session of approximately 20 minutes. Table 2 shows the number of correct matches over the total number of matches per participant at each game stage. The total number varies according to participants’ need to repeat caves in the game. Unlike the other 30-trial sessions, ABBA consisted of 60 trials due to its low complexity and the opportunities given to participants to handle the mouse and become familiar with the task. Participants’ mistakes in this task were either due to incorrect handling of the mouse or difficulty counting dots on the screen. In the following sessions, we adjusted dominoes images to allow better visualization of dots.
All participants learned taught relations and showed the emergence of tested ones. Except for P3 and P5, participants required additional matching trials in ACCA (number-to-number-operations and number-operations-to-number) to meet the 80% criterion. P1 faced a programming error (consequences were shown in some BCCB test trials). We then decided to reintroduce ACCA teaching and perform a new BCCB test without feedback.
After reaching 90% in ACCA teaching, P2 performed the BCCB test. He scored 66.6% in BC (sets of dots to operations with digits). Therefore, we decided to reintroduce ACCA teaching, in which he scored 100%. We then introduced a new BCCB test session, but his performance on CB in operations with the unknown in position c was 66.6%. We finally reintroduced ACCA teaching - in which he scored 100% - and a new BCCB test session. Before starting the test, the researcher asked P2 how to solve the operations with unknowns in the different positions. The researcher reinforced correct explanations with praise and clarified doubts about the algorithm for solving the operations. P2 then performed a new BCCB test and scored 100%.
Participants in post-intervention phases (Figure 3) showed increased performance in solving operations, both with digits and scales. Regarding positions of the unknowns, only P4 showed decreased performance with the unknown in position b in scale operations. Although some variation occurred in the percentage of correct responses, results in follow-up sessions remained above those observed at pretest. Notably, some participants showed increased performance in some operations (P3 and P4 in scale operations with the unknown in position b; P5 in digit operations with the unknown in position b and scale operations with the unknown in position a). Figure 4 shows participants’ errors concerning the position of the unknowns in teaching and test phases.
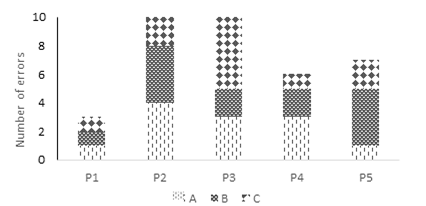
Except for P1 - which showed a similar number of errors in all positions of the unknowns - and P3 - for whom errors were more frequent in position c - the others showed more frequent errors in positions a or b. Table 3 presents engagement and usability assessment data.
In usability (Table 3), the comment rate is higher for questions about the game. Although this type of comment was present in all sessions, it was more frequent in ACCA teaching. Despite its low rate, some participants requested help performing game activities - highest for P3 - and this frequently happened in test sessions. As for high engagement behaviors, higher rates were observed in solving operations, another commentary about the game, and commenting on plot/story. Solving operations verbally was more frequent in the initial sessions (ACCA and BCCB). Comments on the plot/story were directed to characters, the treasure trail, and game tasks. Other comments about the game were related to responses like naming numbers, describing how the problems were solved, and so forth (see Table 3).
Low engagement comments were less frequent than high engagement categories. There was only one request to interrupt the activity made by P1 in DBBD. Finally, comments on topics outside the game were made only by P1, P2, and P5. Figure 5 shows the percentage of help requested by each participant throughout the experiment.
Except for P5, who needed more supervision-like assistance (40.7%), all others performed most activities independently. Moderate assistance was more frequent in ACCA teaching sessions. Figure 6 shows the percentage of operations performed with and without the aid of rods in taught and tested relations throughout the game.
All participants used rods to solve operations across sessions. More operations were solved without help, except for P1 (in ACCA, and BCCB) and P2 (in ACCA, and DBBD). Notably, no participant used the aid of rods to perform ABBA, and DCCD relations due to the task nature [matching numerals with sets of dots (ABBA), and matching digit operations to scale operations (DCCD)], which is why it does not appear in the Figure. We also noted a decreased use of rods to aid the resolution of operations. Informal observations suggest that this decrease was gradual for some participants. They initially used rods, then just looked at the cups and rods while solving the operations without handling them, and finally moved on to solving the operations without looking at or handling the cups and rods.
Discussion
This study evaluated the effects of an adapted digital domino game, based on the stimulus equivalence paradigm, developed for teaching relationships between numerals (A), sets of dots (B), and multiplication operations with digits (C) and in a scale format (D). All participants learned taught relations and demonstrated the emergence of tested ones, just as in studies that used Korsan to teach addition (Gris et al., 2018) and subtraction (Godoy, 2018). In this study not all relations were directly taught. The direct teaching of some of them led to the emergence of others, expanding the children's repertoire. Initially independent relations between numerals, sets of dots, digit multiplication operations, and operations in scale format, have become equivalent. The formation of equivalence classes indicates the effectiveness of this paradigm in the teaching of mathematical repertoires, in particular the multiplication teaching. These results are corroborated by Prado and De Rose (1999), and Rossit and Goyos (2009) on the fact that the mathematical repertoire involves a network of relationships. Furthermore, the data obtained in this study reinforce the evidence in the literature about the possibility of using this paradigm for teaching different behaviors (Suzuki & Souza, 2022, Paula & Haydu, 2010).
Comparing the study conducted by Gris (2016) and the study developed by Godoy (2018), who investigated the learning of addition and subtraction operations with the first digital version of the game, in the present research number and average duration of sessions was higher than in previous studies, likely due to the greater complexity of tasks (multiplication versus addition and subtraction). In addition to the derived relations emergence, a comparison between the pre- and post-test data (and follow-up for P3, P4, and P5) also evidence that the participants learned to solve multiplication operations.
Effective teaching programs and educational games should present a gradual increase in task complexity (Linehan et al., 2011). A decrease in help requests throughout the intervention, observed in the present study, suggests that the increase in complexity was planned appropriately. For instance, we programmed the unknowns’ positions to increase tasks' difficulty gradually: first, the game presented the unknown in position c, then b, and finally a. Such an arrangement was not present in previous versions of the game.
Most studies on the role of the unknowns’ position in solving arithmetic problems have been primarily carried out with addition and subtraction operations (García et al., 2006; Hiebert, 1982). However, there is evidence of greater difficulty in problem-solving with the unknowns in initial positions (a or b) for multiplication and division as verified by Henklain et al. (2018) with children from seven to 11 years old. In the present study, participants presented similar difficulties, in line with literature findings.
Studies using games as educational tools generally conduct summative assessments comparing pre- and posttest data (All et al., 2014; Bellotti et al., 2013). The application of questionnaires to assess learning, engagement, and usability is also a common practice in these cases. However, some authors (Bellotti et al., 2013; Bente & Breuer, 2009) argue that evaluations should be embedded into the game when possible (in-game or play-based assessments). Ideally, this assessment pervasively collects data during matches without interfering with players’/learners’ performances (Bente & Breuer, 2009). Assessment should be integrated into the game design process, so previously learned behaviors are employed later to ensure learners’ success (Bellotti et al., 2013). In the present study, the game itself provided part of the learning data through conditional relations testing sessions (i.e., BCCB, ADDA, and DBBD). Supplementary learning assessments were conducted through adapted Lince matches. There are some studies that effectively used different games to teach and evaluate mathematics repertoires (Kiili et al., 2015). In these cases, however, it is important that the "content" of the games be congruent. Future improvements in the game would allow these complementary learning assessments to be integrated into it, allowing an assessment of the effects of this type of manipulation on children's performance in test sessions.
We also planned the usability and engagement throughout the game, without interfering directly in participant's actions during sessions. To this end, we videotaped the sessions for later recording of behaviors indicating engagement and usability. Usability improvements can impact gameplay efficiency (Chang & Johnson, 2021). We proposed adjustments as participants faced difficulties in familiarization sessions (ABBA), mainly regarding stimulus size. Afterwards, behaviors indicating usability problems lowered in frequency, which suggests that changes were suitable. These data - a decrease in the rate of questions about the functioning of the game and requests for help to perform the activities of the game - corroborate those found in other studies that used the equivalence paradigm and games for teaching mathematical skills (Gris & Souza, 2016, Gris et al. 2018) and reading and writing (Suzuki & Souza, 2022). Observing players' behaviors while using the game is important because it allows us to identify usability-related issues and make adjustments to resolve them as quickly as possible. It is emphasized that usability-related problems can produce engagement problems.
The rate of comments on the plot/story shows that the chosen narrative proved adequate for participants. Similar data were found by Godoy (2018), whereas in Gris et al. (2018) this type of comment occurred less frequently. Notably, studies employed different Korsan versions, having Gris et al. used one with the least aesthetic and plot refinements - which may account for the difference in frequency and rate of comments on the story in both studies. Additionally, an elevated rate of problem-solving suggests high engagement of participants in multiplication tasks. Engagement is an important aspect of learning (Jabbar & Felicia, 2015). The stimulus equivalence paradigm has proved to be very effective for teaching different skills. However, in the traditional matching-to-sample (MTS) procedure used in research that employ this paradigm, there is a repetition of trials that can make the task more tiring and less engaging. In turn, when the MTS procedure is presented through a game, the motivational operations promoted by game situations can lead to a greater engagement. In this study and others that used the stimulus equivalence paradigm and gaming, the highest rate of comments of the high engagement category corroborates this statement (e.g., Godoy, 2018, Gris et al., 2018, Suzuki & Souza, 2022).
These results point to integration between game plot and teaching objectives, which is considered a factor that promotes engagement (Silveira, 2019) and better instructional outcomes (Jemmali et al., 2018). Jemmali et al., however, point out that simply creating a game narrative is not sufficient to improve learning and engagement. The story must be integrated into the gameplay as well as the teaching objectives. In our study, multiplication tasks were part of the challenge presented by the storyline, whose ultimate goal was to find the pirate treasure. Assessment performed through Lince maintained the unity of the pirate adventure narrative. We sought to integrate the narrative not only in the digital game, but in the whole intervention.
The use of concrete support materials is also cited in the literature as a problem-solving facilitator (Pires et al., 2013). We observed that the use of cups and rods as an operation-solving resource gradually decreased over the sessions. Initially, they handled rods and sorted them into cups to solve the problems. Then they just looked at the rods and cups while solving without addressing them, and finally, they solved operations without looking at or handling rods and cups. For Skinner (1945), covert behaviors are initially learned overtly. As Simonassi et al. (2001, p. 134) argue, "all behaviors are initially learned in their open form, and only move to a covert condition when appropriate (social) contingencies produce them”. In the absence of a response to solving a problem, participants manipulated objects (rods and cups), thus increasing the likelihood of a response-solution. We infer that the participants formulated rules throughout the sessions, thus requiring no concrete materials to respond to problems. Previously public responses became covert.
Finally, we observed that some participants required more sessions than others at some stages. Different initial repertoires observed at the pretest may explain the differences in the number of sessions for each child to advance through the game. Despite these differences, in the end, all participants learned taught relations, demonstrated the emergence of tested ones, and showed increased rates of multiplication operations, suggesting the effectiveness of the game to teach these operations.
In this study, children performed an average of 30 multiplication operations with the unknowns in different positions. Data show that participants’ comments indicated high engagement. Considering that we tested the first version of the game for multiplication, some aspects can be changed in future studies, namely:
Inclusion of participants with similar initial repertoires. Here, some children had better entry-level repertoires than others. Although all participants’ performances improved over the sessions, more similar pretest performances might indicate more the effects of the game.
Incorporation of more plot elements and reinforcing activities into the game. Future versions of the game could include, for example, earning points for activities performed. The only indication of correct responses was given by the change in color of pieces at the end of a map. Next versions of the game could include minigames, for example, that would only become available if an activity is successfully completed. Progress indicators could also be included (e.g., earning a coin for each activity performed and giving participants the chance to use coins to play a game at the end).
In this study, rods and cups were not integrated into the game. They were presented as concrete handling materials. These elements could be integrated into future versions, and students could use them freely at any stage. This implementation would allow for a more controlled record of the use of this resource to solve problems.