Introducción
1En las últimas décadas han surgido, como resultado de los continuos esfuerzos de investigadores, algunas conceptualizaciones que tratan de responder a los problemas de enseñanza-aprendizaje en el aula de clases. Un caso es el andamiaje (van de Pol et al., 2010), un constructo teórico que cada vez gana más fuerza por sus potenciales beneficios escolares relacionados con la autonomía y la afectividad. Otro caso es el ciclo de aprendizaje de Jorba y Sanmartí (1996), que se ha convertido en un guía para la organización de secuencias didácticas con enfoque constructivista. Sobre estas construcciones teóricas no existen referencias de su aplicación conjunta, sin embargo, en este trabajo se plantea una convergencia entre ellas para la enseñanza de un tema crucial en educación matemática, como son los números racionales.
La convergencia propuesta tiene un valor agregado porque fue implementada en un establecimiento educativo del contexto rural. En medio de las limitaciones propias del campo, la fusión mencionada marca un punto de inflexión por su dinámica interactiva profesor-estudiante, que permite balancear lo cognitivo y socioafectivo y se aproxima al conocimiento matemático desde prácticas socioculturales propias de la ruralidad.
A partir del análisis comparativo del andamiaje y el ciclo de aprendizaje de Jorba y Sanmartí, esta investigación describe un modelo conceptual para su convergencia y lo aplica en la enseñanza de los números racionales a través de una serie de actividades contextualizadas; este marco teórico es abordado en el siguiente apartado. Luego, se exponen la metodología cualitativa usada para el análisis de datos, los instrumentos y una ficha metacognitiva de evaluación que guía el análisis de los resultados. Finalmente, se reseña el impacto de la propuesta en el desempeño y afectividad de los estudiantes y se concluye dando algunas razones para creer que la convergencia es efectiva y pertinente en la escuela rural.
Marco teórico
La primera reflexión seria y sustentada sobre andamiaje se le atribuye a Wood et al. (1976) quienes metafóricamente compararon la función que cumple un andamio en la construcción de un edificio con el andamiaje educativo, es decir, una estructura que ayuda a los estudiantes a realizar una tarea que sin este apoyo no podrían lograr, y que luego se retira. Las revisiones actuales sobre andamiaje lo definen en general como la ayuda temporal suministrada por el docente a sus estudiantes hasta que éstos puedan realizar cierta actividad por su cuenta (van de Pol et al., 2010; Bakker et al., 2015). Estos autores distinguen tres elementos fundamentales de este proceso ordenados progresivamente así: la contingencia, el desvanecimiento y la transferencia de responsabilidad. Se es contingente en la medida que el docente adapta el apoyo según la necesidad del estudiante, paulatinamente este apoyo se desvanece para que la responsabilidad por la tarea se transfiera al aprendiz, ganando autonomía e independencia.
Si bien el andamiaje poco a poco se ha ido insertando en la educación matemática, las investigaciones son todavía incipientes, son escasos los estudios de implementación en el área que miden la efectividad del andamiaje en comparación con la enseñanza regular. No obstante, existen resultados cualitativos y observacionales prometedores que animan a seguir explorando (Wright, 2018; Bakker et al., 2015; Kusmaryono & Wijayanti, 2020; Masinading & Gaylo, 2022).
En efecto, el andamiaje ha sido determinante en diversas investigaciones escolares y universitarias que analizan su implementación en algunas temáticas de las ciencias naturales, sociales y humanas, como por ejemplo la comprensión lectora (Reynolds, 2017), las prácticas científicas (Crujeiras & Jiménez, 2018), la mecánica (López et al., 2018), la solución de problemas en ingeniería (Gómez et al., 2021), la robótica (de Arriba & ParedesVelasco, 2021), la explicación científica escolar (Sommer & Cabello, 2020) y la correlación de rendimiento académico con las emociones (Fernández-Lasarte et al., 2019). Estos estudios señalan una diferencia sustancial e importante de la implementación del andamiaje en la enseñanza de estas áreas y son un estímulo para investigaciones de este tipo en la formación matemática a cualquier nivel y en cualquier contexto.
Con relación al ciclo de aprendizaje de Jorba y Sanmartí (1996), este consiste en unas etapas lógicas para la enseñanza de las ciencias con un enorme potencial en educación matemática, porque sirve para la estructuración metodológica de una secuencia de enseñanza. El aprendizaje en este ciclo sucede en cuatro etapas (Jorba & Sanmartí, 1996; Sanmartí, 2005), que en esta propuesta estructuraron metodológicamente siete actividades de una secuencia de enseñanza, como se especifica a continuación:
La fase de exploración, la cual propone el análisis de situaciones muy simples y concretas cercanas a las vivencias e intereses de los estudiantes. Esta fue aplicada operativamente en este trabajo a través de la Actividad 1, abreviada como (A1).
La fase de introducción de nuevos conocimientos, la cual parte de situaciones concretas e introduce progresivamente los nuevos saberes y el lenguaje abstracto. En la propuesta esta fase se operacionaliza en la segunda y tercera actividad, abreviadas aquí como (A2) y (A3).
La fase de síntesis o estructuración pretende que cada estudiante sea capaz de sintetizar con modelos propios lo aprendido. En este trabajo dicha fase se implementó en las actividades cuarta y quinta, identificadas como (A4) y (A5).
La fase de aplicación es la oportunidad para emplear el conocimiento en situaciones y contextos distintos del que han venido trabajando en clases. Se implementó en este trabajo en las actividades finales, identificadas como (A6) y (A7).
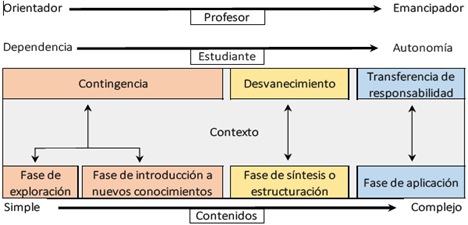
Teniendo en cuenta los referentes teóricos señalados, se estableció el modelo conceptual expuesto en la Figura 1 para ilustrar la convergencia del andamiaje con el ciclo de aprendizaje de Jorba y Sanmartí. El color y las flechas reflejan la correspondencia, como será detallado en la metodología.
El modelo conceptual refleja la afinidad del papel docente y la forma como se ordenan los contenidos en ambos planteamientos teóricos. Por ejemplo, explorar e introducir nuevos saberes son tareas que generalmente atañen al maestro, de igual manera la contingencia ubica al docente como actor principal responsable de diagnosticar continuamente su grupo de estudiantes para devolver respuestas oportunas. Estas devoluciones pueden tanto afianzar el contenido como suplir necesidades afectivas y se materializan a través de la explicación, las preguntas, la retroalimentación, los gestos, las recompensas, entre otros. Luego de un tiempo, se espera que los estudiantes comprendan la importancia del tópico tratado.
Paulatinamente se llega a un punto de equilibrio donde docente y estudiantes están al mismo nivel; por un lado, los aprendices son capaces de elaborar síntesis y modelos personales y comunicarlos usando diferentes registros semióticos, y por el otro, el maestro disminuye la enseñanza contingente y refina puntos claves del contenido. El estudiante se ubica en una zona de intercambio intelectual frente a su profesor, donde este último intenta desvanecerse y el primero independizarse, pero necesitándose mutuamente.
Cuando la etapa anterior ha madurado lo suficiente, el docente puede intencionalmente cohibirse para que los estudiantes asuman el protagonismo de la clase aplicando los saberes en situaciones de aprendizaje escolares y extraescolares. Estas últimas son especialmente difíciles porque los contenidos vistos se ocultan en ellas. Por lo tanto, el final de la convergencia exige entrelazar una serie de anclajes conseguidos en las etapas anteriores para lograr finalmente la autonomía cognitiva y socioafectiva.
El contexto influye en la convergencia porque determina el tipo de actividades que se aplican y la apariencia que puede tomar el andamiaje. Así, el uso de situaciones problémicas contextualizadas favorece la interacción profesor-estudiante a través del diálogo, vinculando saberes previos con los nuevos contenidos para forjar estructuras mentales sólidas con las que se inicie el camino hacia la autonomía. Además, los contextos al ser tan diferentes y específicos hacen que el andamiaje se exprese de diversas formas, convirtiéndose en una especie de abanico que reúne múltiples acepciones; y aunque estas posibilidades lo hacen flexible y facilitan su aplicación, dificultan medir su efectividad.
Vale la pena aclarar que las características del andamiaje y las fases del ciclo de aprendizaje no deben considerarse aisladas ya que, inconsciente o conscientemente, se transita de la una a la otra con actos tan pequeños como una expresión, un gesto o una retroalimentación. También sucede que "al explorar ya se introducen ideas, y al introducir ideas se explora, se estructura y se aplica el conocimiento" (Jorba & Sanmartí, 1996, p. 28). En consecuencia, es posible que estando en un momento final como la transferencia de responsabilidad puedan darse eventualmente pequeñas contingencias, sin embargo, la diferenciación propuesta es necesaria para efectos de planificar las actividades y entender el modelo conceptual de la convergencia.
El contenido elegido para aplicar la convergencia fueron los números racionales porque son esenciales para el aprendizaje de las matemáticas en todos los niveles de educación secundaria, y para la futura comprensión de ideas matemáticas más avanzadas. Cuando en el conjunto de los números enteros se efectúa la división, el resultado no siempre es un número entero; esta limitación se resuelve precisamente garantizando la existencia de un nuevo conjunto numérico, llamado el conjunto de los números racionales.
Un número racional es de la forma - , donde y son números enteros y b 0. Este conjunto se simboliza con la letra Q (Álvarez et al, 2009). Son ejemplo de números racionales las fracciones -> -z~> - y el cociente que se origina de - , que puede generar las siguientes expresiones correspondientes a la representación como un número real:
Decimales finitos: son aquellos cuyo cociente posee una cantidad finita de cifras decimales. Ejemplos de estas son: 0.125, 12.32 y -15.36457, entre otros.
Decimales infinitos periódicos: son aquellos que poseen una cantidad infinita de cifras decimales las cuales se repiten periódicamente. Por ejemplo, 1.3333 ... que se puede escribir como 1-3, -0.252525... que se puede escribir como-0.25 y 12.712323... que se puede escribir como , 12.7123 entre otros. Aquí el símbolo "A" significa que el conjunto de cifras debajo de este se repite indefinidamente.
La forma - de los números racionales ha originado múltiples interpretaciones, entre las que se citan parte-todo, cociente, razón, medida, y operador (Kieren, 1976). Esta naturaleza polisémica del concepto se ha vuelto un desafío para quienes intentan enseñarlo y quienes buscan comprenderlo (Elias et al., 2020). El número racional parece ser un concepto difícil (Park & Esposito, 2022) que por sus diversos matices y complejidades atrae la investigación actual.
En este sentido, este trabajo representa un esfuerzo por mitigar las múltiples dificultades pedagógicas por las que atraviesan docentes y discentes cuando enfrentan la enseñanza-aprendizaje del número racional. La convergencia de los elementos del andamiaje y del ciclo de aprendizaje de Jorba y Sanmartí se proyecta como una oportunidad para lograrlo.
Metodología
Para este estudio se empleó una metodología cualitativa con enfoque descriptivo e interpretativo (Sandín, 2003) por sus posibilidades para indagar, profundizar y describir la interacción profesor-estudiante en el aula de clases. Participaron voluntariamente nueve estudiantes a quienes inicialmente se les aplicó una prueba diagnóstica escrita, con el fin de identificar los conceptos previos relacionados con fracciones como contenido fundamental de los números racionales; luego, se implementó una unidad didáctica diseñada siguiendo la convergencia de la Figura 1, la cual contenía siete actividades (A1, A2,..., A7) inspiradas en situaciones propias del campo y cercanas a la vida cotidiana del estudiante, relacionadas con la siembra y división de terrenos agrícolas, los valores, dichos populares y la manipulación de material concreto. Esta unidad didáctica fue proporcionada a los estudiantes a través de una guía didáctica impresa.
Durante la intervención se registraron los hechos relevantes en cada actividad en el diario de campo docente y se incentivó a los estudiantes a la producción escrita a través de sus bitácoras. Como actividad de cierre, se aplicó una autoevaluación tipo Likert (Matas, 2018; Clark & Watson, 2019) que valoró el impacto académico y socioafectivo del proceso. En el análisis de la información se usó la triangulación de datos (Hernández-Sampieri & Mendoza, 2018) y se tomaron como categorías los elementos del andamiaje y las fases del ciclo de aprendizaje de Jorba y Sanmartí (1996).
Para evaluar el impacto de la convergencia y los resultados de la unidad didáctica se construyó la ficha metacognitiva de evaluación, mostrada en la Tabla 1, que integró el marco teórico, las actividades, los desempeños del estudiante y el papel del docente. Su estructura se ciñe a la convergencia descrita en la Figura 1. De forma más precisa, el color rojo indica que las actividades están en correspondencia con la contingencia y las fases de exploración e introducción. El color amarillo, abarca las actividades de desvanecimiento y fase de síntesis. Finalmente, el color azul indica las actividades de transferencia de responsabilidad y fase de aplicación. Este código de colores es indispensable para el análisis de los hallazgos, ya que la guía didáctica fue impresa siguiendo este código.
Tabla 1 Ficha metacognitiva de evaluación
| Característica del andamiaje | Fases del ciclo de aprendizaje | Desempeños del estudiante | Acciones del docente |
| Contingencia | Exploración (A1) | (A1) Distribuye el terreno de la huerta escolar siguiendo las especificaciones dadas. (A1) Determina la fracción que corresponde a cada producto. | Valora los conocimientos previos del estudiante. Apoya a los estudiantes en la interpretación de las fracciones para que distribuyan el terreno de la huerta escolar. |
| Introducción de nuevos conocimientos (A2 y A3) | (A2) Identifica la equivalencia entre las fracciones encontradas al doblar hojas de papel. (A3) Descubre la expresión decimal de una fracción emparejando barras. | Ejemplifica los dobleces de la primera hoja. Hace seguimiento a las estrategias adoptadas por los estudiantes y los dirige hacia el logro del objetivo planteado. | |
| Desvanecimiento | Síntesis (A4 y A5) | (A4) Determina la fracción equivalente a través de la distribución gráfica de la siembra de plátanos. (A5) Representa una fracción de forma gráfica, numérica y decimal. | Valida el proceso del estudiante y lo reorienta de ser necesario. Indica puntos de mejora en algunos casos. |
| (A6) Descubre un mensaje reduciendo | Espera sin intervenir y al final verifica el procedimiento aplicado en la eje- | ||
| Transferencia de responsabilidad | Aplicación | fracciones a su mínima expresión. | |
| (A6 y A7) | (A7) Descifra un refrán haciendo con- | cución que realiza el estudiante y da indicaciones en casos de confusión. | |
| versiones de fracción a decimal. |
Resultados
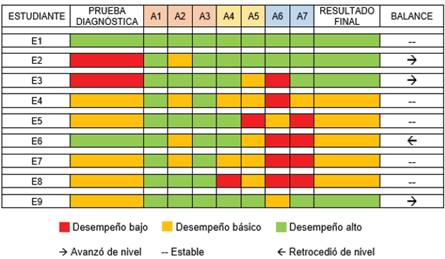
A través de la Figura 2 se ilustra un panorama general de los resultados obtenidos al culminar la unidad didáctica, resaltando el punto de partida de cada estudiante, el recorrido por las actividades y su estado final luego de la implementación.
Como se observa en la Figura 2, en la prueba diagnóstica la mayoría se situó en niveles de desempeño bajo y básico debido a la dificultad para representar fracciones gráficamente. Las representaciones más acertadas fueron las relacionadas con fracciones que indicaban mitades, en contraste, los mayores desaciertos surgieron al representar fracciones referidas a un cuarto o tres cuartos. Algunos de los errores más frecuentes fueron:
Dividir la unidad en partes que no fueron iguales.
Fraccionar la unidad, pero no tomar las partes solicitadas.
Representar intuitivamente la fracción, sin demarcar las partes en que se divide la unidad.
Con relación a las siete actividades, hubo dos estudiantes que pasaron de nivel bajo a nivel alto con solvencia. Cuatro estudiantes del nivel básico no consiguieron avanzar al siguiente nivel, como se esperaba, puesto que dependían en gran medida del apoyo docente en las actividades que implicaban autonomía. Un estudiante retrocedió del nivel alto al nivel básico; esto también se debió a la incapacidad para desenvolverse por sí mismo en aquellas actividades que así lo exigían. Los estudiantes E1 y E9 comprendieron bien el tema y se ubicaron al final en el mejor nivel. Es destacable que finalizada la intervención no existan estudiantes clasificados en desempeño bajo.
La actividad A1 correspondió a la fase de exploración y buscaba que el estudiante interpretara las fracciones como parte-todo de un conjunto desde el contexto de la huerta escolar. En su desarrollo, el docente mantuvo un rol contingente, es decir, de apoyo total. Partiendo de unas especificaciones dadas, los estudiantes determinaron las cantidades de terreno a sembrar de seis cultivos distintos con la ayuda del docente. En aquellas especificaciones referidas a quinta o cuarta parte fue necesario aumentar el soporte porque se presentaron complicaciones para dividir. Acto seguido, expusieron su creatividad creando un plano para la huerta, después identificaron la fracción correspondiente de cada sembrado. La siguiente Figura 3 muestra dos casos diferentes:
El docente tuvo que explicar esta parte ya que al principio comparaban un cultivo con respecto a otro y no con respecto a la totalidad de la huerta, es decir que no lograban ver la unidad como un todo. Al final comprendieron que producir diseños distintos no cambiaba la fracción de terreno destinado a cada cultivo. Los objetivos de la fase de exploración planteados en la primera actividad se lograron totalmente, puesto que, desde el contexto de la huerta escolar, los estudiantes tuvieron una visión global y simple de las fracciones como uno de los contenidos representativos y fundamentales de los números racionales. Se identificó como punto de mejora el concepto de unidad ya que no lo reconocieron en objetos cotidianos susceptibles de ser fraccionados. En general, el apoyo constante del docente facilitó el alcance de los desempeños.
Seguidamente se inició la fase de introducción a nuevos conocimientos con la actividad A2, con el fin de comprender la equivalencia entre fracciones. El docente entregó dos hojas de papel por estudiante y actuó solucionando dudas constantemente: la Hoja 1 la doblaron por la mitad y la Hoja 2 en tres partes iguales, pintaron la mitad de la primera y la tercera parte de la segunda, luego hicieron dobleces sucesivos por la mitad en ambos casos. Los primeros cuatro dobleces los pudieron representar en forma gráfica y fraccionaria sin problemas, pero en el quinto y sexto doblez estuvieron confundidos porque las hojas no se dejaban doblar con facilidad y esto los obligó a recurrir a su intuición para tratar de imaginar lo que verían. Se observó que solo cinco de los nueve estudiantes iban por buen camino por lo que el docente intervino para retroalimentar y guiarlos en la consecución del objetivo. La interacción en el aula estuvo mediada por el uso de cuestionamientos que llevaron a los estudiantes a reconocer que en cada una de las hojas las fracciones encontradas indicaban la misma parte coloreada y, por lo tanto, eran equivalentes.
La introducción a nuevos conocimientos se cerró con la actividad A3, ideada para comprender la relación de las fracciones con los números decimales. El docente continuó en su papel contingente e introdujo un nuevo conocimiento, a saber: las expresiones decimales. Para ello, hizo uso de barras rotuladas con números fraccionarios y decimales, y pudo apreciar que los estudiantes, guiados por el mismo tamaño en las barras, emparejaron y descubrieron la expresión decimal de ocho fracciones distintas. El apoyo docente permitió que todos los estudiantes entendieran el algoritmo de la división con cociente decimal, pero a nivel individual se apreciaron dificultades para dividir.
En la segunda fase del ciclo los propósitos fueron alcanzados parcialmente porque en la actividad A2 solo cinco estudiantes pudieron identificar la equivalencia entre las fracciones que se generan al doblar las hojas de papel, y en la actividad A3, todos lograron descubrir la expresión decimal de las fracciones indicadas. De esta manera, los saberes introducidos forjaron el concepto de número racional y mejoraron la habilidad procedimental. El docente a través del diagnóstico continuo reafirmó lo aprendido y logró buenos resultados.
Se prosiguió con la fase de estructuración y síntesis por medio de la actividad A4, con la intención de reconocer la equivalencia de fracciones en situaciones reales y de manera analítica; de aquí en adelante comenzó el desvanecimiento docente. Los estudiantes representaron siembras de plátano equivalentes en tres terrenos subdivididos en seis, nueve y dieciocho partes iguales, pero notaron que en uno de ellos había algo que no encajaba, ya que no podían representar la mitad de la siembra con una fracción con denominador 9. Precisamente, el desequilibrio de este ejercicio consistía en percatarse de que no existe una fracción equivalente a 3/6 o 9/18 con denominador 9. Es decir, ninguno logró advertir que la fracción sembrada de plátano en uno de los terrenos no podía determinarse. Con la disminución de la asistencia docente se escucharon frases como "no sabemos que hacer"; en estos casos, el docente no cedió y mantuvo un soporte decreciente, actuando en concordancia con la convergencia propuesta.
En la actividad A5 el docente continuó retirando gradualmente el apoyo a los estudiantes; aquí se cierra la fase de síntesis. Se buscó comprender gráfica y algorítmicamente la conversión de una fracción a número decimal e interiorizar el concepto de décima y centésima; para ello, se usó una cuadrícula 10x10 y granos de lenteja. Ante la escaza ayuda docente, hubo muchas dificultades en los criterios de divisibilidad y la incapacidad para dividir. Aun así, todos lograron distinguir los diferentes números decimales representados en la cuadrícula, menos aquella que ilustraba la totalidad de esta, la cual quedó de la forma 100/100, y mencionaron que dicha fracción era igual a 0,100 en lugar de 1. A lo mejor, como venían obteniendo una secuencia de números decimales donde la parte entera era 0, pasaron por alto que llenar toda la cuadrícula con lentejas equivalía a representar la unidad.
Las actividades A4 y A5 permiten concluir que la fase de estructuración y síntesis tuvo un alcance parcial de los objetivos, ya que en la cuarta actividad varios estudiantes lograron determinar las fracciones equivalentes en los terrenos a cultivar plátano, pero ninguno pudo identificar el caso en que una fracción deja de ser equivalente a otras. Y en la quinta actividad, una minoría pudo representar gráfica y decimalmente las fracciones indicadas; el resto, aunque gráficamente lo hicieron bien, fallaron en la representación decimal porque erraban en la división. En esta fase el docente poco a poco se desvaneció y aparecieron por primera vez estudiantes con desempeño bajo.
La culminación del desvanecimiento abrió paso a la fase de aplicación; etapa en la que el docente transfirió la responsabilidad a sus estudiantes. Primero se trabajó la actividad A6 con el fin de reducir fracciones a su mínima expresión; se propuso descifrar un mensaje oculto con ayuda de un abecedario donde cada letra se asoció a una fracción reducida. Aquí la mayoría de estudiantes se quedaron esperando el apoyo necesario para salir de la confusión, pero el docente se mantuvo firme en su papel de no brindar ayuda y los motivó a continuar por su cuenta. Por esta razón, solo fue concluida por dos estudiantes.
El cierre de la intervención se dio por medio de la actividad A7, que trabajó habilidades para convertir fracciones en números decimales; el docente se cohibió de cooperar e instó a trabajar autónomamente. Los estudiantes relacionaron fracciones en su expresión decimal con una secuencia de imágenes para obtener dos refranes populares, pero en vista de que ninguno pudo descifrar el primer dicho, pese a que cuatro de ellos acertaron la secuencia de imágenes correctas para hacerlo, pidió que lo inventaran. Una de las creaciones fue "la mano del hombre coge una paloma, la paloma es de suerte y te puedes ir de viaje" mientras que el deseado era "Más vale pájaro en mano que cien volando". Un solo estudiante logró descifrar el segundo refrán "A caballo regalado no se le mira el colmillo". Esta séptima actividad generó cierta frustración por su dificultad, sin embargo, el final fue muy divertido porque los adagios inventados causaron muchas carcajadas.
Las falencias en la división y las dificultades en comprensión de texto hicieron que el menor alcance de objetivos se diera en la fase de aplicación (A6 y A7). Por la misma intención de las actividades parte de la tarea estuvo en leer y comprender la situación de manera independiente, no obstante, a algunos estudiantes les costó porque leían y no ejecutaban, antes bien preguntaban al docente qué había que hacer. Se cree que el rendimiento bajo de algunos participantes en esta última fase está asociado al poco tiempo dedicado en las etapas de desvanecimiento y transferencia de responsabilidad. Siendo precisos, históricamente estos estudiantes poco o nada han trabajado bajo metodologías autónomas en el aula de clases, en ese sentido es probable que su proceso de adaptación haya sido lento. No se pone en duda su capacidad para el aprendizaje de estos temas, pero algunas prácticas educativas inciden de manera positiva o negativa en la comprensión del saber, como lo evidencia esta investigación.
En general, la fase de aplicación dejó al descubierto una marcada diferencia entre los ritmos de aprendizaje de los nueve participantes, puesto que aquellos en nivel de desempeño alto demostraron una gran destreza procedimental y no dependieron del docente; contrario a lo ocurrido con estudiantes en nivel de desempeño bajo, quienes erraron operativamente y fueron inseguros al retirarse el apoyo docente.
Análisis de la convergencia a través del desempeño
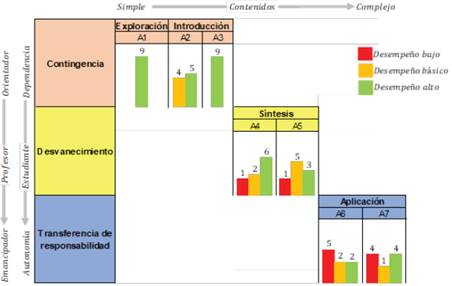
En la Figura 4 convergen las características del andamiaje con las fases del ciclo de aprendizaje de Jorba y Sanmartí (1996). Las barras indican el número de estudiantes que obtuvieron desempeños bajo, básico o alto en cada una de las actividades.
De la anterior Figura 4 es posible inferir que la retirada paulatina del soporte resultó ser provechosa para algunos e inconveniente para otros. Por ejemplo, hubo estudiantes que plantearon bien los procedimientos, pero erraron en la parte operativa por descuido y por no tener la aprobación del profesor en cada paso. En cambio, otros demostraron apropiación de la temática y lograron emanciparse.
La revisión minuciosa de las actividades permitió concluir que durante la enseñanza contingente los estudiantes lograron solucionar el 93% de las actividades, en el desvanecimiento resolvieron el 80%, y en la etapa autónoma, este porcentaje disminuyó hasta ubicarse en un 51%. Hubo evidentemente una correlación entre el retiro paulatino del andamio y la disminución progresiva de actividades resueltas.
El andamiaje posibilitó a los estudiantes ganar confianza y mejorar el dominio cognitivo y conductual sobre sí mismos a medida que avanzaron hacia la etapa de transferencia de responsabilidad. Por su parte, el ciclo de aprendizaje guio el desarrollo de las actividades yendo de lo simple a lo complejo, o lo que es lo mismo, partiendo de lo concreto a lo abstracto; esto más desde la mirada de Jorba y Sanmartí (1996). Por eso, en las primeras actividades los estudiantes se acercaron a los números racionales a través de la manipulación de material concreto, y en las últimas se enfocaron en lograr las abstracciones necesarias para asegurar la comprensión del tópico, demostrando así un cierto progreso desde el punto de partida.
Impacto socioafectivo
En primer lugar, el docente basado en la ficha metacognitiva de la Tabla 1 moderó su aptitud para ajustarse a la convergencia propuesta y tuvo cuidado con las expresiones, gestos y el material concreto que se utilizó en la intervención. Esta apropiación del marco teórico fue muy importante para saber responder socialmente al grupo de participantes.
Es sorprendente que un cambio en la forma tradicional de enseñar propicie un comportamiento distinto en el estudiante dentro del proceso formativo (Bernal & Martínez, 2017; Cevikbas & Kaiser, 2022). En este sentido, se pudo observar que los estudiantes exteriorizaron sus ideas y sentimientos verbalmente, con dibujos y mediante escritura, lo cual fue fundamental en su proceso de independencia porque cada uno encontró la forma de expresarse y de interrelacionarse con los demás. La convergencia promovió el aprendizaje colaborativo y la socialización, de manera que se valoraron los puntos de vista y opiniones entre compañeros como sujetos activos.
Más aún, algunos estudiantes manifestaron que las actividades estuvieron muy por encima de sus expectativas iniciales y que lo aprendido superó, en contenido y satisfacción, todo lo que hasta ese momento habían aprendido en grados previos. Este disfrute y satisfacción quedó en evidencia por el cuidado que dieron a los insumos, la cercanía y compañerismo expresado a sus pares.
En definitiva, la convergencia del andamiaje y el ciclo de Jorba y Sanmartí dejó en evidencia el carácter integrador de las componentes académicas y socioafectivas que proporciona este vínculo. Ciertamente, la convergencia permitió a los estudiantes alcanzar niveles de competencia superiores en su formación matemática e impactó positivamente lo relacionado a las emociones y sentimientos personales. Prueba de ello es que en la fase de aplicación ningún estudiante abandonó el propósito de las actividades, pese a la frustración causada por la complejidad de las mismas y la ausencia del apoyo docente. Aunque no todos consiguieron el objetivo cognitivo esperado sí lograron mantener la motivación y perseveraron por aprender a su propio ritmo. Con estos hallazgos se hace un aporte a la creciente preocupación actual por averiguar la relación entre socioafectividad y educación en ciencias, tanto en docentes como en estudiantes, dada su influencia en la enseñanza y el aprendizaje (Romero et al., 2021; Bieg et al., 2017; Castillo, 2011).
Conclusiones
La evidencia empírica y descriptiva revelada muestra que la convergencia entre andamiaje y ciclo de aprendizaje de Jorba y Sanmartí es efectiva en educación matemática. La conjunción favoreció el aspecto cognitivo porque hizo frecuente la devolución-regulación por parte del profesor, y en consecuencia hubo aprendizajes significativos de los números racionales ya que los estudiantes crearon conciencia del concepto y sus formas de representación, dejaron atrás algunas ideas erróneas sobre el tema y adquirieron mayor destreza para tratar la división y la simplificación. No obstante, fue evidente que el retiro paulatino del apoyo docente influyó en una disminución de los desempeños, pero en general, la fusión benefició la motivación y tolerancia a la frustración cuando esto sucedió.
La convergencia se adaptó bien al contexto de la escuela rural porque permitió suplir las necesidades de estudiantes con distintos ritmos de aprendizaje que necesitaron de apoyos graduados personalizados. Lo anterior fue un reto que se pudo sobrellevar gracias a las bondades de la fusión que permite planear sesiones de clase con esta intención. Ahora se sabe que la convergencia propuesta está en sintonía con los fines de la educación y, por consiguiente, podría integrarse y potenciar algunos modelos educativos flexibles vigentes en Colombia como escuela nueva, postprimaria, media rural, entre otros.
Se apreció que en la práctica docente subyace un ejercicio de diagnosis continua que permite la comprensión individual y grupal para ejecutar devoluciones efectivas. El estudiante hace también este esfuerzo de comprensión hacia su docente para lograr finalmente el aprendizaje autónomo; de esta manera, se da una cierta comprensión bilateral que parece garantizar de momento el éxito de la convergencia pero que merece más atención en futuras investigaciones