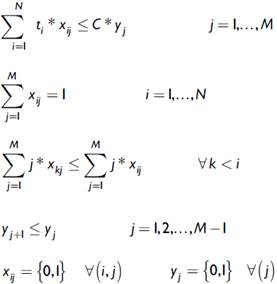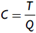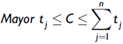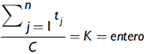La producción en línea se relaciona con la fabricación de grandes cantidades de productos estandarizados, que se organizan en líneas de ensamble que, de acuerdo con Cabrera y González (2019), se caracteriza por tratarse de operaciones vinculadas a estaciones de trabajo donde las piezas que visitan las estaciones son intervenidas de manera secuencial para conformar un producto. Los problemas de equilibrio de la línea de ensamblaje son una tarea importante en la planificación de la producción de mediano plazo (Becker y Scholl, 2006), entendiendo que la gestión de este tipo de sistemas productivos está relacionada como lo mencionan Gurevsky, Battaïa y Dolgui (2012) y Pereira y Álvarez-Miranda (2018), con la eficiencia y la capacidad de producción, el inventario en proceso, la calidad del producto, la asignación de recursos y el control de flujos, entre otros aspectos que se vuelven determinantes en la competitividad de cualquier organización. Por su parte, Ozbakir, Baykasoglu, Gorkemli y Gorkemili (2011) así como Baykasoglu, Özbakir, Görkemli y Görkemli (2012) mencionan que el balance de línea hace un gran aporte en la reducción de fallas y aumento de la productividad, lo que mejora la flexibilidad y competitividad de una compañía en un mercado cada vez más complejo. La producción en línea está comúnmente presente en las industrias de manufactura y tiene el propósito de reducir costos en la producción en masa, donde son requeridas líneas de producción altamente eficientes y flexibles con base en su adecuado diseño y balanceo.
Una línea de ensamble consiste en estaciones de trabajo k = 1,…, m usualmente ubicadas a lo largo de una banda transportadora. Las piezas de trabajo son colocadas en la línea y movidas de estación en estación, de tal forma que en cada una se desarrollan operaciones iguales de manera repetitiva de acuerdo con un tiempo de ciclo, el cual es definido en Fucci (2014) como el tiempo máximo o promedio disponible para cada ciclo de trabajo.
Tal como se describe en Polat, Mutlu y Özgormus (2018), la manufactura de un producto en una línea de ensamble requiere dividir la cantidad total de trabajo en un conjunto V = {1,…,n} de operaciones elementales llamadas tareas. Además, desarrollar una tarea j toma un tiempo de tarea t ¡ y requiere máquinas o habilidades de los operarios para realizarse. La cantidad de trabajo total necesaria para ensamblar una pieza de trabajo es medida como la suma de los tiempos de tarea t sum . Debido a las condiciones tecnológicas y organizacionales, se deben considerar restricciones de precedencia entre tareas. El problema de balanceo de línea de ensamble (ALBP), tal como lo mencionan Nourmohammadi, Fathi y Ng (2019), consiste en hallar un balance de línea (asignación de cada tarea a una estación) tal que se cumplan restricciones de precedencia, entre otras restricciones.
Existen diversas clasificaciones de los problemas de balanceo de línea que permiten describir los aspectos particulares considerados en cada uno, tal como lo plantean Zuluaga-Ramírez y Gómez-Suta (2016) y Gansterer y Hartl (2018), quienes hacen una revisión sobre las diferentes clasificaciones presentadas en la literatura. En este sentido, se identifica a Baybars (1986) quien propone una clasificación en la que se distinguen dos tipos de problemas clásicos: el simple (SALBP) y el general (GALBP); en la que plantean cuatro categorías de modelos de balance de línea: modelo simple determinístico, modelo simple estocástico, modelo multi/mixto determinístico y modelo multi/mixto estocástico. La siguiente clasificación presentada en la figura 1, recopila las propuestas de Baybars (1986) y también las de Scholl (1999), Pinto, Dannenbring y Khumawala (1983), Rekiek et al. (2002) y Becker y Scholl (2006), referidas también en Peltokorpi, Tokola y Niemi (2012), Battaïa y Dolgui (2013), Battaïa, Delorme, Dolgui, Frédéric y Finel (2015), Yolmeh y Kianfar (2012), Otto, Otto y Scholl (2013), Hamzadayi y Yildiz (2012), Akpinar y Baykasog lu (2014) y en González, Simonetti, Michelon, Martinhon y Santos (2016).
A fin de generar mayor claridad con los desarrollos presentados en este artículo y los escenarios que se desarrollarán, se presenta la definición de Restrepo, Medina y Cruz (2008), Pitakaso y Sethanan (2016) y Bappy, Musa y Hossain (2019) para los cuatro casos de SALBP:
SALBP-1: consiste en asignar un conjunto de tareas a las estaciones de tal forma que se minimice el número de estaciones, dado un tiempo de ciclo (o tasa de producción). Este caso se presenta habitualmente cuando un nuevo sistema de montaje se va a instalar y la demanda externa puede ser estimada. Trabajos como los de Sungur y Yavuz (2015), referencian estudios clásicos como Jackson (1956), Dar-El (1975), Mastor (1970), Pinto, Dannenbring y Khumawala (1975), Wee y Magazine (1981a), Chutima y Prasert (2018) y Johnson (1973) abordan este problema.
SALBP-2: busca minimizar el tiempo de ciclo o equivalentemente, maximizar la tasa de producción, dado un número de estaciones fijo. Se considera que la línea de montaje ya existe. Mastor (1970), Wee y Magazine (1981b) y Chutima y Yothaboriban (2017) presentan desarrollos de este tema, así como Scholl y Klein (1997).
SALBP-E: maximiza la eficiencia E de la línea; esto es, minimiza el producto de m (número de estaciones) por c (tiempo de ciclo), estudiado en Jusop y Rashid (2015), Corominas, García y Pastor (2016), Kuzmin y Haritonova (2019) y Salama, Abdelhalim y Eltawil (2017).
SALBP-F: consiste en determinar si existe alguna solución factible para la combinación de un número m de estaciones y un tiempo de ciclo c; es decir, se quiere conocer si la línea puede operar con m estaciones y un tiempo de ciclo c dados. El SALBP-F ha sido trabajado en Alavidoost, Zarandi, Tarimoradi y Nemati (2017), Kamarudin y Rashid (2018), Huo, Wang, Chan, Lee y Strandhagen (2018) y Vidondo (2019), entre otros.
En el desarrollo de este documento, se tomará como objeto de estudio uno de los casos tratados en Servin (2004) y referido también en Pascual-García (2015); en donde se propone un método heurístico que resuelve el problema SALBP-1 para la industria de vestidos en México, mostrando las posibilidades existentes de solución mediante un algoritmo genético híbrido (AG) simple que incluye la técnica de lógica difusa (LD) en el proceso de evaluación. El algoritmo genético se entiende como un método adaptativo que busca encontrar soluciones cada vez más óptimas, tomando como principio el proceso de la genética de los seres vivos donde sobreviven los más fuertes (Hernández, 2019). Entre tanto, la lógica difusa se trata de una lógica multivaluada que de acuerdo con Cubides, García, Marín, Caracas y López (2018), permite utilizar valoraciones más allá de las binarias de sí o no, verdadero o falso, entre otras, que facilitan cálculos más precisos y cercanos a la realidad.
Los datos serán usados para aplicar un método analítico de solución que permite determinar los valores óptimos de cada problema, propuesto por los autores, ampliando la aplicación a un problema SALBP-2 y, por último, al SALBP-F. Dado que Servin (2004) solo aplica la metodología para el problema SALBP-1, en este trabajo se presenta la solución analítica para los tres casos del SALBP usando el lenguaje de programación AMPL, después de haber abordado la solución para el SALBP-1 y SALBP-2 con el uso de algunas heurísticas, con el propósito de comparar los resultados en procura de validar la precisión de los métodos heurísticos. Finalmente, se concluye de acuerdo con los resultados obtenidos.
Caso de estudio
El caso de Servin (2004) tomado para el desarrollo de este trabajo, describe el proceso de elaboración de una prenda de vestir considerando un conjunto de tareas que presentan restricciones de precedencia, además de la agrupación de las tareas de diversas formas dentro de su proceso de producción, debido a su naturaleza discreta. En este caso de estudio se considera una empresa que elabora diferentes prendas de vestir. Estas prendas son fabricadas en módulos o líneas de producción, entendidas como una serie de máquinas agrupadas, con las cuales se pueden realizar todas las tareas necesarias para fabricar una prenda de vestir, de manera que permita empezar y terminar la prenda en esas máquinas.
El problema del balanceo de un módulo de confección consiste en asignar las tareas necesarias a los operarios, para fabricar una prenda, de manera que las cargas de trabajo y los tiempos necesarios para realizar las operaciones asignadas a cada operario, sean lo más equilibrado posible, es decir, que se utilicen los recursos de la mejor manera. Esta empresa cuenta con 15 módulos o líneas de confección; para este trabajo se tomará el módulo o línea de producción de pantalones, para ser analizado.
Los primeros pasos en el ensamble de prendas se conocen como preparación de las piezas o subensamble, después se realiza el ensamble y por último el terminado o acabado de la prenda, que logra un aspecto presentable y adecuado de la misma para el consumidor. Según Servin (2004), no es común encontrar empresas que utilicen métodos analíticos para hacer el equilibrado de líneas, frecuentemente recurren a la intuición y al cálculo aproximado. Además, en la industria de manufactura, tal como lo mencionan Zaman, Imtiaz y Motaleb (2018), balancear una línea de ensamble, trata del diseño de un flujo de producción fluido mediante la asignación de tareas a los trabajadores para permitir que cada trabajador complete la carga de trabajo asignada en un tiempo uniforme, buscando la misma cantidad de trabajo y evitando sobrecargas y esperas.
A continuación, se presentan los pasos clásicos que se desarrollan en una línea dentro de un taller de confecciones, considerando además que el método puede tener variación dependiendo de la empresa que elabore la prenda.
Operaciones necesarias para realizar la prenda
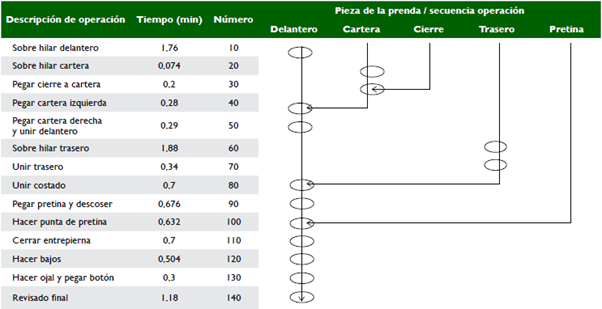
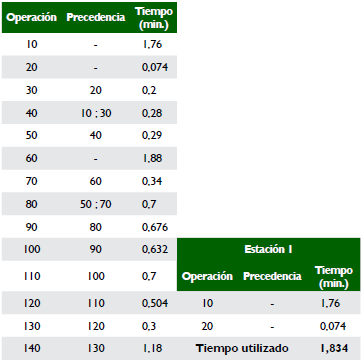
En primera instancia debe realizarse el desglose de las operaciones, lo que permite establecer el número y tipo de piezas. Para este caso, tomando el proceso de ensamble de pantalones de caballero, cuyos componentes se encuentran consolidados en la tabla 1, primero se analizan las operaciones de preparación sin las que es imposible continuar con el ensamble. Se enumeran las operaciones en orden ascendente, y cada operación tiene asignado un tiempo, partiendo para este estudio del supuesto de que el tiempo es independiente de la máquina en la que se realice la operación. El pantalón de caballero tradicional está siendo considerado como producto estándar, y aunque actualmente existen muchos estilos, se describen las piezas del producto tradicional Blue Jean. De igual manera, se considera que su fabricación durante una temporada es de 1.000 pantalones diariamente.
En la figura 2 se presentan los elementos que forman parte de un pantalón convencional, con el propósito de familiarizarse con las denominaciones.
Es importante precisar que las operaciones que se toman como referencia pueden tener sus variaciones dependiendo del taller de confecciones; sin embargo, las características propias de esta línea objeto de estudio, se pueden enumerar como siguen:
Se produce de una manera secuencial y unidireccional.
Se dispone de un grupo de máquinas y operarios, divididos en estaciones que realizan distintas operaciones.
Los tiempos de las operaciones están definidos y estandarizados.
Producen un número elevado de prendas; es decir, los lotes de producción son grandes.
Se tiene una secuencia de operaciones las cuales deben cumplirse (precedencia) (véase tabla 2).
Diagrama de operaciones
A continuación, se detallan los datos más importantes sobre la prenda y se muestran las operaciones requeridas para su elaboración. En la tabla 3 se muestra la agrupación de las operaciones, con su descripción y el tiempo asociado a cada operación, así como el tiempo total requerido para la fabricación de un pantalón.
Con esta información se da inicio a la aplicación de dos métodos heurísticos para obtener el balanceo del SALBP-1 y SALBP-2, con el propósito de tener una base de comparación de los resultados que se obtendrán con la aplicación del método analítico y poder validar la información obtenida a partir de la consulta bibliográfica sobre la efectividad de estos métodos heurísticos.
Implementación de algoritmos
Con los datos presentados en el apartado anterior se procede a implementar los algoritmos correspondientes a cada configuración del problema SALBP. En primera instancia, se utilizará el algoritmo COMSOAL estudiado en Orozco, García y Grisales (2016), Díaz (2017) y Lozano, Miño y Mariño (2018), entre otros autores, para el modelo SALBP-1; y posteriormente el método de Kilbridge y Wester estudiado en Salazar y Santa (2013), Medina-Chacón (2014), Meneses (2014) y Sánchez (2017), entre otros autores, para el SALBP-2. Luego con los resultados obtenidos se procederá a mostrar las posibles soluciones para el problema SALBP-F. Por último, se aplicará el método analítico con el uso de programación con el lenguaje AMPL, para comparar los resultados, este último aplicado para solucionar el SALBP-1, SALBP-2 y SALBP-F.
Algoritmo COMSOAL (computer method for sequencing operations for assembly lines)
Durante el proceso de documentación bibliográfica se encuentra que en algunos de los trabajos de Restrepo et al. (2008), Galofre-Vásquez, Mejía-Ávila y Acuña-Molina (2012), así como en Lozano et al. (2018), tratan problemas de balanceo SALBP-1 y SALBP-2, con el uso de algunos heurísticos entre los que se destaca el algoritmo COMSOAL, que a pesar de ser un procedimiento que data de los años sesenta, es todavía aplicado con resultados muy eficientes. El algoritmo COMSOAL según lo presentan autores como Arcus (1966), Kucukkoc, Karaoglan y Zhang (2018) y Chen et al. (2019) es un método algorítmico que aunque no garantiza llegar al óptimo; ofrece resultados aceptables y útiles. COMSOAL emplea un método de generación de secuencias, donde las tareas son clasificadas según su peso posicional, con base en el tiempo más largo de funcionamiento (LOT), el tiempo más corto de funcionamiento (SHOT), la mayor cantidad de las tareas siguientes y menor número de las tareas siguientes. Arcus (1996) y Chen et al. (2019) describen el funcionamiento del COMSOAL en siete pasos. Por otra parte, en su trabajo, Restrepo et al. (2008) resumen el algoritmo COMSOAL en seis pasos, que se presentan a continuación y que serán los tomados para la aplicación a este caso de estudio. Son ellos:
Para cada tarea identifique las tareas que le siguen inmediatamente o preceden inmediatamente.
Crear una lista A con las tareas no asignadas, sus predecesoras inmediatas (no asignadas) y el número total de tareas que la preceden (no asignadas).
De la lista A cree una lista B conformada por las tareas que tienen cero (0) predecesores. Si no hay tarea sin ser asignada a estaciones entonces pare.
De la lista B, cree una lista C compuesta de las tareas que tienen tiempo de proceso que no supera el tiempo disponible de la estación. Si la lista C está vacía, abra una nueva estación y repita el paso b.
Aleatoriamente seleccione de la lista C una tarea para asignarla a la estación.
Actualice el tiempo disponible en la estación y la lista A. Retorne al paso c.
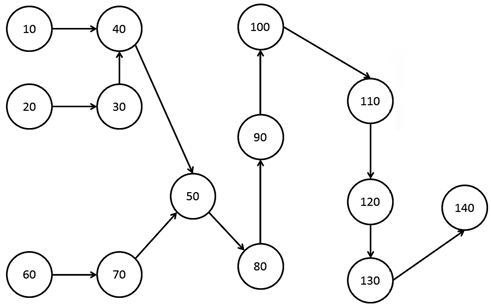
En este sentido, se identifican las tareas con sus respectivas precedencias, es decir, aquellas tareas que preceden o siguen inmediatamente (véase tabla 4).
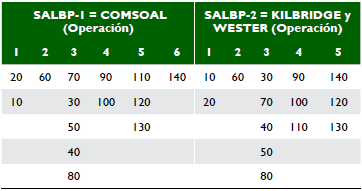
Se realizan secuencialmente los pasos ya descritos hasta obtener una asignación completa de las tareas, esto dio lugar a 14 iteraciones (véase figura 3) de las cuales el resultado final es el que se muestra en la tabla 5.
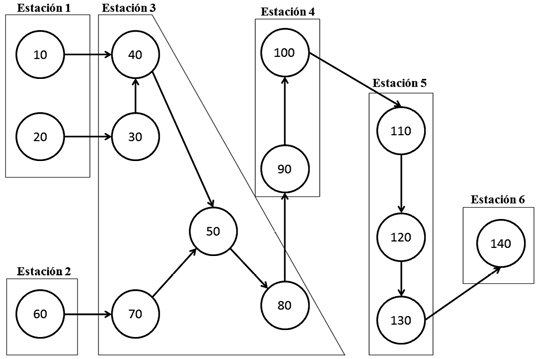
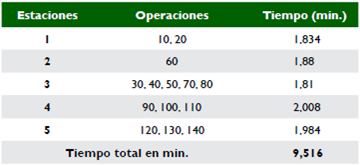
La aplicación del algoritmo finalmente arrojó un tiempo de ciclo asignado de 1,880 min con un número de estaciones de trabajo asignadas por el algoritmo de 6. En la figura 4 se muestran las operaciones asignadas a cada una de las seis estaciones de trabajo.
Método de Kilbridge y Wester para SALBP-2
Este método es aplicado para el problema tipo 2 del SALBP, básicamente porque propone minimizar el tiempo ocioso de una línea, lo que permite acercarse a una solución donde se obtiene un número de estaciones con el mejor tiempo de ciclo posible dentro de su alcance. La solución se obtiene mediante la aplicación de los siguientes pasos planteados en Kilbridge y Wester (1996):
Construir un diagrama de precedencia, como se observa en la tabla 4.
Determinar un tamaño de ciclo (C). El tamaño de ciclo se puede definir con el fin de cumplir con una demanda o tasa de producción esperada o minimizar el tiempo ocioso de la línea.
Con esta información se empieza asignando las tareas que no tengan precedencias, hasta que se cubra la disponibilidad de cada centro de trabajo teniendo en cuenta la restricción de tiempo. Se crea entonces una lista con las tareas no asignadas, luego se escogen las que no tengan precedencias asignando tantas tareas como sea posible teniendo en cuenta el orden en que deben realizarse.
El proceso se repite hasta que todas las operaciones queden asignadas a sus estaciones de trabajo (véase tabla 6).
Después de la primera iteración se asignan las tareas 10 y 20 a la estación 1 (véase tabla 7).
En la estación 2 será asignada la tarea 60. Se continúan las iteraciones hasta que la totalidad de tareas sean asignadas a las diferentes estaciones. En total se realizan cinco iteraciones, terminando así la asignación de tareas, se obtuvieron los resultados presentados en la tabla 8.
En la figura 5 se presenta la distribución de operaciones por estaciones de trabajo obtenidas por este método.
Comparación de resultados
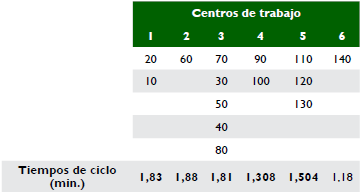
En la tabla 9 es posible ver las diferencias de asignación de tareas en los modelos de acuerdo con los algoritmos empleados. En ambos casos, las mismas operaciones son asignadas a los centros de trabajo 1, 2 y 3, mientras que para los centros de trabajo 4 y 5 se presentan algunas variaciones; obedeciendo a las restricciones de tiempo de ciclo obtenido en el SALBP-1, se tiene un número de centros de trabajo mayor que en el SALBP-2, diferencia que se presenta debido a que el tiempo de ciclo en el primero es menor.
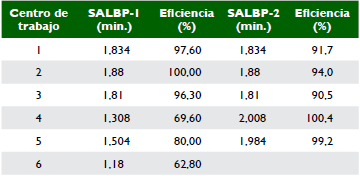
Considerando que los dos aspectos más importantes en el balanceo de líneas de ensamble son la tasa de producción y la eficiencia, se calcula la eficiencia de las soluciones obtenidas para cada centro de trabajo, tomando como base para el SALBP-1 un tiempo de ciclo C = 1,88 min y para el SALBP-2 un tiempo de ciclo C = 2 min. Los resultados se presentan en la tabla 10.
A pesar de que los dos modelos y métodos son distintos, como se puede ver en la tabla 10, se obtienen tiempos de ciclo idénticos para las primeras tres estaciones de trabajo, y variación en los tiempos de ciclo siguientes. Aunque se obtuvieron resultados similares, cabe resaltar que en el método de Kilbridge y Wester aplicado al SALBP-2 existen eficiencias mayores que en el otro método. En este sentido, las eficiencias pueden motivar la elección de un arreglo como el planeado para el SALBP-2. Sin embargo, en el ambiente de la implementación se deben considerar situaciones de espacio y viabilidad práctica de las operaciones, que al final se convierten en determinantes al momento de tomar la decisión.
Por otra parte, se realiza el cálculo de la eficiencia global para estas soluciones, donde se obtienen los siguientes resultados usando la fórmula de cálculo que se presenta a continuación:
Como se observa en la tabla 11, los resultados obtenidos también evidencian una mejor eficiencia global para la solución del SALBP-2, lo logra a pesar de que el tiempo de ciclo es mayor al tomado como referencia para el SALBP-1.
Esto se explica con base en el mayor tiempo disponible por ciclo, lo que permite finalmente una mayor ocupación de las estaciones con las tareas propias de la labor. Estos resultados sugieren, además, que para este caso, una variación de tiempo de ciclo, puede facilitar una división del trabajo más equitativa entre las estaciones de trabajo. Lo anterior habría que validarlo en el plano real, cuando el tomador de decisiones se enfrente al problema.
Formulación de modelos matemáticos: soluciones analíticas
En este apartado se presentan los modelos matemáticos referidos al SALBP-1, SALBP-2 y SALBP-F. Se solucionan utilizando el lenguaje AMPL, con objeto de obtener las soluciones analíticas para los problemas de balanceo tipificados. Es importante resaltar que la mayor dificultad en la programación de este tipo de problemas en este lenguaje se ve reflejada en la restricción de precedencia, para la cual se debe considerar un conjunto especial, que contenga todas las posibles relaciones de precedencia entre las tareas, modificando la variable de decisión "x" y de esta manera lograr que el modelo asigne las tareas en la secuencia correcta.
Modelo matemático para SALBP-1
Variables de decisión
Parámetros
t i = tiempo de proceso de la tarea i
C = tiempo de ciclo
Función objetivo
Restricciones
El modelo de programación propuesto se plantea en lenguaje AMPL y se resuelve utilizando el solver de CBC en el servidor de NEOS, obteniendo los resultados que se presentan en la tabla 12.
El problema contempla 150 variables (todas binarias); 37 restricciones lineales; 14 restricciones de igualdad; 23 restricciones de desigualdad; 1 objetivo lineal. Utilizando un tiempo de ciclo de 1,88 min, se obtuvo un número máximo de seis centros de trabajo y se realizaron 39.584 iteraciones en 2,92 min, con la asignación presentada en la tabla 13.
Al comparar la eficiencia de las soluciones obtenidas por el método analítico y por el COMSOAL, se observa que se obtiene una eficiencia global igual a 84,36%, que se explica debido a que en ambos casos se trabaja con un tiempo de ciclo C = 1,88, que como se debe recordar es un dato de entrada en el SALBP-1. Sin embargo, al observar las eficiencias de los centros de trabajo en particular consolidadas en la tabla 14, se pueden identificar diferencias importantes en las eficiencias parciales.
La más notoria se presenta en la estación de trabajo No. 2 con una diferencia en la eficiencia del 59,04% por debajo el método analítico con respecto al algorítmico. Los datos arrojados por el algoritmo COMSOAL, muestran un tiempo ocioso en las operaciones 4 de 30,43%, 5 de 20% y en la operación 6 de 37,23%, que frente a la demanda de trabajo adicional por fuera de la estación de trabajo puede limitar el uso de los operarios para soportar estas actividades. El método analítico concentra en la estación 2 el mayor tiempo ocioso (59,04%), seguida por la estación 6 (21,3%), lo que puede facilitar la asignación de actividades adicionales, no consideradas en el balanceo a los trabajadores de estas estaciones.
Modelo matemático para SALBP-2
Variables de decisión
C = tiempo de ciclo
Parámetros
t i = tiempo de proceso de la tarea i
Función objetivo
Min C
Restricciones
Resultados obtenidos a partir del solver CBC de NEOS se presentan en la tabla 15.
El problema contempla 85 variables, 84 de ellas binarias, 1 variable lineal; 33 restricciones lineales; 14 restricciones de igualdad; 19 restricciones de desigualdad; 1 objetivo lineal. Con un número máximo de estaciones de trabajo igual a seis, se obtuvo un tiempo de ciclo óptimo de 1,88 en 3.868 iteraciones en 0,43 segundos.
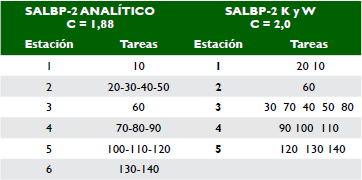
Observando los resultados de ambos modelos aplicando el método analítico, es posible notar que de acuerdo con el tipo de problema la manera en que se asignan las tareas puede variar, pero los resultados obtenidos en cuanto a tiempo de ciclo y estaciones de trabajo son los mismos, para este caso. En la tabla 16 se reportan los resultados obtenidos por el método analítico y los obtenidos con el algoritmo de Kilbridge y Wester, donde se observa el número de estaciones abiertas con el método analítico de seis en comparación con cinco reportadas por la solución algorítmica.
Al hacer el cálculo de las eficiencias globales de las soluciones, encontramos que la eficiencia obtenida por el método analítico es de 84,36% y por el método de Kilbridge y Wester es de 95,16%. Lo anterior se explica precisamente porque el segundo método parte de un tiempo de ciclo no óptimo, que permite al final un mejor arreglo en función de los tiempos ociosos que se puedan presentar en la línea. Para explicarlo de manera más detallada, es necesario recordar que el método heurístico plantea que se debe tener el tiempo de ciclo (C), el cual debe cumplir con dos objetivos:
a. Una demanda o tasa de producción esperada que se determina con:
Donde se define:
T = Tiempo disponible de producción en un periodo conocido en minutos por dia o en horas por mes
Q = Unidades requeridas a producir en el periodo T expresadas en unidades por dia, o unidades por mes
b. Un tiempo de ciclo (que debe ser un número entero) que minimice el tiempo ocioso, de tal manera que C debe ser:
Mayor t j < C < ^ t j
Se debe recordar que el balance perfecto se obtiene cuando:
Es evidente que la solución óptima es obtenida con el método analítico (véase tabla 17), pues el tiempo de ciclo calculado es el mínimo y óptimo, mientras que el tiempo de ciclo calculado por el método heurístico está viciado, pues en cualquier caso debe aproximarse al entero más próximo. Este procedimiento cambia la configuración de la línea y altera los datos de eficiencia.
Para entender aún mejor el porqué de los resultados, vale la pena recordar el sentido del problema típico SALBP-2, el cual busca minimizar el tiempo de ciclo, dado un número de estaciones fijas. El procedimiento desarrollado para el SALBP-2 analítico, utilizó los resultados obtenidos como estaciones de trabajo óptimas en el SALBP-1, que arrojó un número óptimo de seis estaciones, que como bien se recuerda se tomaron como dato de entrada para el desarrollo de la solución para el problema SALBP-2.
Para efectos de validar este punto, se realiza la corrida analítica con el uso del lenguaje de programación AMPL con un dato de entrada para el SALBP-2 de cinco estaciones de trabajo, con los siguientes resultados (véase tabla 18).
Se trabajan 71 variables, 70 binarias, 1 variable lineal, 32 restricciones lineales; 275 no ceros, 14 restricciones de igualdad y 18 restricciones de desigualdad, 1 objetivo lineal. Tiempo de ciclo óptimo 2,008 min, con 3.033 iteraciones, 0,310953 segundos.
Como se observa en la solución, el tiempo óptimo de ciclo obtenido es de 2,008 min, cercano al asignado con el método de Kilbridge y Wester, el cual fue de 2 min, con base en la aproximación con números primos. Nuevamente se hace evidente que la asignación al entero más próximo propuesto por el heurístico afecta el resultado de eficiencias obtenido arriba. La asignación de tareas por estaciones de trabajo se presenta en la tabla 19.
Tiempo total (min.) 9,516
Obsérvese ahora como queda la distribución en eficiencia y su comparación con los resultados obtenidos por la solución algorítmica.
Observando los datos de la tabla 20, y comparando las soluciones, persiste una diferencia mínima entre la solución algorítmica y analítica, ambas con cinco estaciones, con eficiencias la primera de 95,16% y 94,78% la segunda, lo que arroja una diferencia de 0,379% que puede considerarse despreciable, ya que en términos de tiempo 520 min por turno (tiempo por turno referenciado por Servin, 2004), equivalen a 1,97144 minutos por turno. Sin embargo, de nuevo se debe precisar que esta diferencia surge como producto del procedimiento propio del algoritmo, dado que Kilbridge y Wester proponen expresar el tiempo de ciclo como un número primo aproximando en caso de valores decimales a un número entero, que lo mencionan como una condición necesaria pero no suficiente, que permite determinar el número de estaciones, a priori, ajustando a través de los pasos del algoritmo los tiempos asignados a cada estación de trabajo. Por ejemplo, para este caso de estudio el tiempo de ciclo se asigna con un límite inferior tj de 1,88 min que se aproxima a 2 min y un límite superior igual a la  que para este caso es de 9,516 min y que se aproxima al entero 10 min. Como se observa en el procedimiento, entre las alternativas posibles de tiempo de ciclo, se seleccionan 2 min de tal manera que al entero K = Σ tj / C = 5 estaciones, le serán asignadas operaciones cuya sumatoria de tiempo sea igual a 2 min máximo en este número de estaciones de trabajo calculadas. Lo que se puede observar es que en la estación de trabajo 4 el algoritmo asigna operaciones equivalentes a 2,008 min, ligeramente superior al tope máximo de 2 min, debido a que no encuentra un arreglo de operaciones que permite distribuir este tiempo exactamente igual máximo a 2 min sin la necesidad de abrir otra estación de trabajo. Lo anterior muestra que, aunque el tiempo es despreciable, el procedimiento heurístico no arroja una solución exacta. También se hace evidente que el número de estaciones mejora de manera sustancial el desempeño de las eficiencias, como se puede observar al correr la solución analística para el SALBP-2 con datos de entrada de seis y cinco estaciones, respectivamente; lo que permite, en el segundo caso, obtener un tiempo de ciclo mayor que impacta de forma sustancial la eficiencia, como se presenta la tabla 21.
que para este caso es de 9,516 min y que se aproxima al entero 10 min. Como se observa en el procedimiento, entre las alternativas posibles de tiempo de ciclo, se seleccionan 2 min de tal manera que al entero K = Σ tj / C = 5 estaciones, le serán asignadas operaciones cuya sumatoria de tiempo sea igual a 2 min máximo en este número de estaciones de trabajo calculadas. Lo que se puede observar es que en la estación de trabajo 4 el algoritmo asigna operaciones equivalentes a 2,008 min, ligeramente superior al tope máximo de 2 min, debido a que no encuentra un arreglo de operaciones que permite distribuir este tiempo exactamente igual máximo a 2 min sin la necesidad de abrir otra estación de trabajo. Lo anterior muestra que, aunque el tiempo es despreciable, el procedimiento heurístico no arroja una solución exacta. También se hace evidente que el número de estaciones mejora de manera sustancial el desempeño de las eficiencias, como se puede observar al correr la solución analística para el SALBP-2 con datos de entrada de seis y cinco estaciones, respectivamente; lo que permite, en el segundo caso, obtener un tiempo de ciclo mayor que impacta de forma sustancial la eficiencia, como se presenta la tabla 21.
Tabla 20 Comparación eficiencias por el método analítico vs. Kilbridge y Wester para SALBP-2 con cinco estaciones
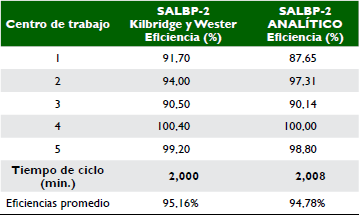
Tabla 21 Comparación eficiencias obtenidas por el método analítico SALBP-2 para seis y cinco estaciones de trabajo

El tiempo óptimo con el método analítico para el caso con seis estaciones es de 1,88 min y de 2,008 min para el caso de cinco estaciones que, para el modelo heurístico es de 2 min, se trata de una solución aproximada, aunque bastante eficiente.
Modelo matemático para SALBP-1
Antes de mostrar los resultados de la formulación multiobjetivo propuesta para abordar este problema, es conveniente retomar los aspectos característicos de este problema. Por tratarse de un SALBP-F, se encuentran dos objetivos contrapuestos; es decir, por una parte, se tiene la necesidad de obtener un número óptimo de estaciones de trabajo y, por otra, un número óptimo de tiempo de ciclo.
Se hacen algunas pruebas con diferentes datos partiendo de los siguientes supuestos:
Los datos de estaciones de trabajo son discretos, es decir, se trata de números enteros.
Los tiempos asignados a las operaciones son continuos con un mínimo de tiempo de ciclo factible de 1,88 min y un tiempo máximo de 9,516 min, que corresponde a la sumatoria de tiempos de las diferentes operaciones.
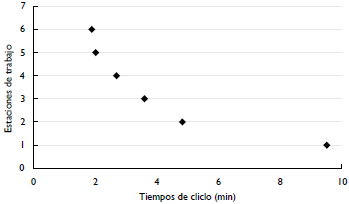
A partir de estos supuestos se generan datos crecientes del tiempo en el rango de los tiempos mínimos y máximos de la operación, para ver el comportamiento del número de estaciones obtenidas para el problema SAL-BP-1. La figura 6 muestra los resultados, que permiten ver gráficamente cómo para datos asociados a diferentes tiempos de ciclo, el número de estaciones de trabajo no aumenta, dado que todas las operaciones pueden desarrollarse con holgura con las estaciones definidas.

Figura 6 Representación gráfica de las estaciones de trabajo para diferentes tiempos de ciclo en el SALBP-1.
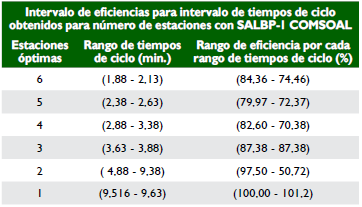
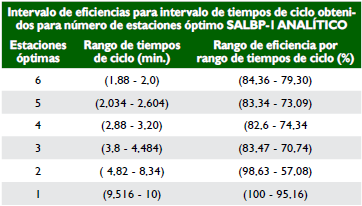
De la misma forma, al calcular las eficiencias para estos puntos, se observa que la mejor se obtiene en el rango de tiempo de ciclo explorado de (3,63 - 3,88) min, con una eficiencia de 87,38% para cuatro estaciones de trabajo. Sin embargo, para el caso de estudio se trabaja con un tiempo de ciclo de 1,88 min que genera una eficiencia de 84,36% (véase tabla 22), lo que arroja un número de estaciones m = 6, como la mejor solución para este tiempo de ciclo.
Desde la perspectiva de la frontera de Pareto, se trata de obtener aquellos datos que son factibles para la relación tiempos de ciclo y estaciones de trabajo viables.
Al graficar los datos obtenidos de tiempos de ciclo para un número de estaciones discretas conocido, se puede observar en la figura 7 una frontera que corresponde a las estaciones exactas, que precisamente por tratarse de datos discretos, corresponde a una sola solución, de acuerdo con el número de estaciones que se corra en el modelo.

Fuente: los autores.
Figura 7 Representación gráfica de los tiempos de ciclo para un número de estaciones dado SALBP-2.
SALBP-F debe arrojar una solución que corresponda a los datos que coincidan para las diferentes soluciones SALBP-1 y SALBP-2, y se deben convertir en la frontera de Pareto.
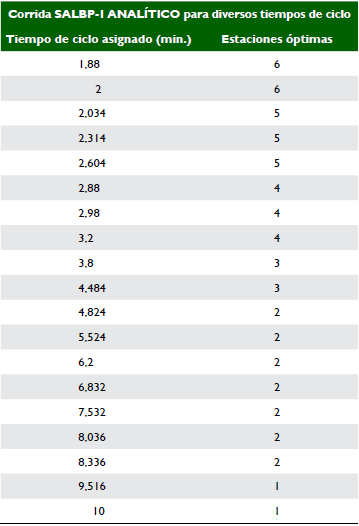
Haciendo las diferentes corridas con el AMPL para el SALBP-1 con objeto de obtener las soluciones de estaciones de trabajo óptimas asignándoles tiempos de ciclo en el rango de tiempo de 1,88 min y 10 min, que corresponden a los extremos del tiempo para la elaboración de las operaciones de la prenda de vestir, se obtienen los datos presentados en la tabla 23.
Como se observa en los datos, existen rangos de tiempo donde las estaciones óptimas se mantienen, aunque el tiempo de ciclo cambie. La figura 8 permite apreciar esta situación.
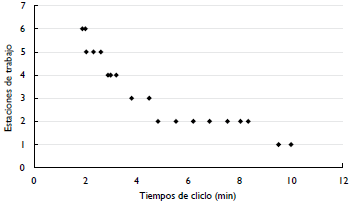
Figura 8 Representación gráfica del número de estaciones con tiempos de ciclo dado SALBP-1 obtenidos por el método analítico
Efectivamente, el comportamiento de las soluciones es de la forma esperada, cuando se trata de obtener soluciones de estaciones de trabajo para diferentes tiempos de ciclo. Como se observa en la tabla 24, el rango de eficiencias logra valores más cercanos entre ellos (los extremos del rango son menos distantes), en el rango de tiempos de ciclo (2,88 - 3,20) min con cuatro estaciones de trabajo. Sin embargo, para el tiempo de ciclo seleccionado de 1,88 min el número óptimo de estaciones es m = 6.
A partir de este análisis se espera determinar con el método analítico las soluciones que sean coincidentes para cada uno de los objetivos planteados en el SALBP-1 y SALBP-2, con el propósito de encontrar el conjunto de parejas de tiempo de ciclo (c) y estaciones (m), que puedan ser de uso por el tomador de decisiones, que sería el resultado esperado para el SALBP-F.
A continuación, y en el mismo caso que los otros modelos, se utiliza el solver CBC de NEOS para encontrar las soluciones, donde se obtienen los resultados que se presentan en la figura 9 y que corresponden a soluciones factibles de tiempos de ciclo y estaciones de trabajo para el SALBP-1 y SALBP-2. Además, se calcula la eficiencia de cada combinación, con el fin de utilizar dicha información como el posible criterio de elección de la mejor combinación a criterio del tomador de decisiones.
Tal como lo mencionan Baesler et al. (2008), el tomador de la decisión deberá evaluar la conveniencia de usar una u otra alternativa, con base, incluso, en las eficiencias obtenidas. Evidentemente, la solución con la eficiencia mayor es el número de estaciones de 1, que corresponde a una solución trivial. Para efectos del análisis con los datos obtenidos para el SALBP-1 y el SALBP-2 tratados como problemas independientes, se puede observar con los datos obtenidos que la mejor eficiencia se consigue con la solución de cinco estaciones con un valor de 94,78% y un tiempo de ciclo óptimo de 2,008 min.
Al comparar las soluciones obtenidas de las parejas (c, m), factibles para atender los dos objetivos (9,516;1), (4,824;2), (3,596;3), (2,684;4), (2,008;5), (1,88;6) (véase tabla 25) y comparándolo con la solución óptima del SALBP-1 analítico y SALBP-2 analítico que es (1,88;6), se observa que este punto es una solución contenida dentro de las factibles arrojadas por el modelo SALBP-F; pero no sería la más eficiente para el conjunto de las dos funciones objetivo en función a la eficiencia. La que propone mejor desempeño sería la combinación (2,008;5), que además se acerca mucho al resultado propuesto por el método Kilbridge y Wester, con las consideraciones que se discutieron en el aparte correspondiente.
Comparación de resultados obtenidos frente a la solución presentada en Servin (2004)
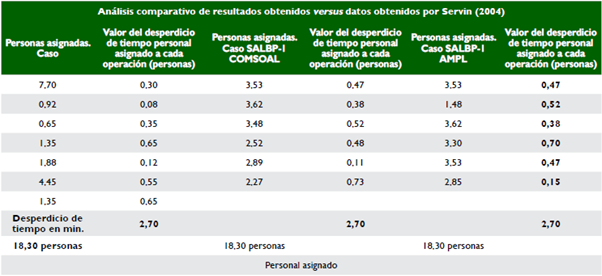
A continuación, se comparan los resultados obtenidos por Servin (2004) con los arrojados en este trabajo, y se aclara que la solución del autor referenciado está en función a la asignación de personal a sus estaciones de trabajo. Para hacer el análisis comparativo, se llevarán las conclusiones obtenidas a la asignación de personal, utilizando los mismos criterios del autor en cuanto al tiempo disponible por turno de 520 min (Servin, 2004) y las piezas a producir por turno de 1.000 unidades.
Para efectos de hacer el análisis comparativo, se presenta a continuación, en las tablas 26A y 26B, la solución mostrada en el caso de Servin (2004), en número de personas asignadas, con respecto a la asignación que se haría para cada una de las soluciones obtenidas en este trabajo con el uso de las herramientas algorítmicas y analíticas.
Para ilustrar lo mencionado, la primera columna muestra el personal asignado por estación de trabajo y en la siguiente se calcula el desperdicio de tiempo que se plantea con esta asignación, comparando la asignación neta respecto al número entero siguiente que correspondería a las personas físicamente que se asignarían en la realidad.
Es evidente que este análisis no es exactamente el que operaría en la vida real, pues allí se involucrarían análisis subjetivos, de complementariedad de tiempos de operación y demás; pero se considera válido en términos de análisis comparativo de datos netos obtenidos, toda vez que la asignación de tiempos complementarios sería objeto de otro problema.
Como se puede observar, la presentación se hace para los resultados de la solución planteada en Servin (2004) y para cada una de las soluciones propuestas por los métodos COMSOAL, Kilbridge y Wester, SALBP-1 analítico, SALBP-2 analítico para seis y cinco estaciones, asignando el número de personas con la misma metodología de Servin (2004).
El número de personas se calcula, multiplicando el tiempo en minutos asignado para cada estación de trabajo por la producción de 1.000 unidades por turno, y dividiendo por el tiempo de trabajo por turno de 520 min.
De acuerdo con los datos obtenidos con este análisis comparativo, se puede observar que los tiempos perdidos en las opciones presentadas por la solución original, la obtenida con el uso de COMSOAL para el SALBP-1 y para la solución analítica con número de estaciones m = 6, reportan una sobreasignación de 2,7 personas, por lo que se podría plantear que estas soluciones son equivalente. Sin embargo, al observar los resultados dados por el algoritmo Kilbridge y Wester para el SALBP-2 y el método analítico SALBP-2 con un número de estaciones m = 5, la sobreasignación de personal es de 1,7 personas, lo que sugiere que estas son las mejores alternativas de solución.
En términos del SALBP-F, existe una coincidencia con el análisis hecho en el aparte respectivo, pues la solución más conveniente a partir de la mejor eficiencia obtenida para la solución tiempo de ciclo y número de estaciones (c, m) dentro de las soluciones factibles, igual a (5; 2,008), corresponde a la mejor asignación de personal, de acuerdo con lo analizado arriba.
Conclusiones
De acuerdo con los resultados obtenidos, se puede concluir que las soluciones óptimas no necesariamente ofrecen soluciones más eficientes en el desempeño de la línea, cuando los problemas son tratados de manera independiente como SALBP-1 y SALBP-2. En el primer caso, si los tiempos de tareas son cercanos o se pueden agrupar en valores muy cercanos al tiempo de ciclo óptimo, como en el caso del heurístico Kilbridge y Wester, es posible obtener soluciones en número de estaciones óptimas a pesar de que el tiempo de ciclo no sea necesariamente el óptimo. En el segundo caso, si el tiempo de ciclo llegase a ser cercano al óptimo, puede suceder que el número de estaciones se reduzca, lo que produce una mayor eficiencia de la línea en términos de tiempos ociosos. En tal sentido, el tiempo de ciclo óptimo no estaría garantizando necesariamente una mejor eficiencia de la línea de producción en conjunto. Sin embargo, se corre el riesgo de que en la práctica se presenten limitaciones en la fluidez de las operaciones, pues finalmente no se trabaja con los óptimos.
La determinación del mejor número de estaciones de trabajo a partir de un tiempo de ciclo conocido, se trató como un problema SALBP-1, con los algoritmos COMSOAL y el método analítico. Lo observado con estas soluciones es que su resultado usando el mismo tiempo de ciclo c = 1,88 para ambos métodos, arroja el mismo número de estaciones m = 6, e incluso con eficiencias globales iguales de 84,36% para cada uno de los métodos. Esto sugiere que el método heurístico es muy eficiente, para instancias como esta, si el dato de entrada del tiempo de ciclo es el mismo. Además, se observa que a pesar de que los resultados en estaciones de trabajo y eficiencia global son iguales, las rutas de ensamble son distintas, característica que es necesario considerar como parte de la caracterización de cualquier problema de balanceo de líneas.
Con base en los resultados reportados en este trabajo, tratando el problema como un SALBP-2, para identificar el mejor tiempo de ciclo de acuerdo con un número de estaciones dadas, se pudo evidenciar que el algoritmo de Kilbridge y Wester, obtuvo una muy buena solución en términos de eficiencia, al igual que el método analítico, con soluciones muy similares. En esta solución se resalta que el método heurístico propuso un resultado basado en un tiempo de ciclo igual a un número entero de 2 min, que no se ajustaba exactamente a un tiempo de ciclo asociado a una operación o a un conjunto de tiempos de operaciones; situación que, con el método analítico, se evidenció como una solución exacta, asignando un tiempo de ciclo de 2,008 min que se ajustaba perfectamente a los datos de tiempos disponibles. Esto deja claro que el método analítico arroja óptimos resultados; que el algoritmo usado en este caso, no lo consigue a pesar de que la solución en número de estaciones sea la misma.
Durante el proceso de investigación se muestra que se han realizado avances importante en algoritmos para resolver el tipo de problemas SALBP, además de tratarse de un problema de optimización NP-hard, se encuentran algunos procedimientos exactos y heurísticos ya desarrollados para resolver este tipo de problemas en un tamaño sencillo, aunque para instancias de mayor tamaño falta desarrollar métodos eficaces.
Para la función bi-objetivo planteada para el SALBP-F se utilizó como enfoque de solución la optimalidad de Pareto. Esta es una herramienta muy útil para efectos de identificar los valores de frontera o que dominan en el objetivo de optimización (minimización en este caso) a otras alternativas posibles de solución. Sin embargo, en este caso, el método se simplifica, pues una de las variables de las posibles parejas de solución [estaciones de trabajo (m), tiempo de ciclo (c)] es discreta, lo que define en todo caso un único valor óptimo en tiempo de ciclo para el número de estaciones definidas (variable discreta). La solución, entonces, en el escenario práctico, estará definida por la decisión del analista en consideración a la utilidad que valide, de cada una de ellas.
Finalmente, debe decirse que existen múltiples configuraciones de líneas, que efectivamente deben ser estudiadas, con el propósito de ofrecer soluciones óptimas. Sin embargo, el aporte de este trabajo plantea la formulación de una solución analítica para el SALBP-F, que podría eventualmente usarse para problemas con un grado de complejidad mayor al caso estudiado en este documento para validar el modelo. Además, al validar los resultados obtenidos, se pudo establecer que para el SALBP-2 y el SALBP-F, la mejor solución en exactitud y asignación de recursos de personas a las estaciones de trabajo, se logró con mayor eficiencia a través de los métodos analíticos con un número de personas sobrantes de 1,7 frente a 2,7 en promedio resultantes de la sobreasignación de personal, incluso en la solución planteada para este problema en Servin (2004).