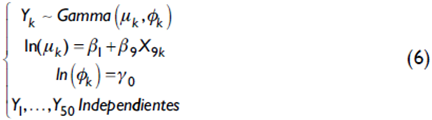El Grupo de Investigación GEOTOPO1 realizó el diseño metodológico de esta investigación, que sometió a prueba de campo y el propósito fue estudiar la exactitud de los datos capturados por un escáner láser terrestre (TLS) marca y referencia Faro Focus 3D (FARO, 2018), perteneciente al laboratorio de topografía de la Universidad Distrital Francisco José de Caldas, en Bogotá, Colombia. El estudio permitió la construcción de un modelo soportado estadísticamente, que comprobó la exactitud de los datos capturados, todo ello en razón a que las especificaciones técnicas del fabricante del escáner mencionado se encuentran delimitadas a unos rangos de distancias entre los 0,6 m y 120 m para los cuales se establece un error sistemático de ± 2 mm por cada intervalo entre 10 m y 25 m. Razón por la cual se presenta la necesidad de hallar un modelo estadístico que permita establecer los rangos de error de los datos adquiridos teniendo en cuenta los ángulos de incidencia (Ramos, Marchamalo & Martínez, 2017; Voegtle & Ruoming, 2009), distancias de captura (Voegtle & Schwab, 2008), y targets u objetivos de captura para el escaneo, para evidenciar de manera estadística la influencia que estas variables tienen en los errores de medición de los datos capturados por un TLS Faro Focus 3D (Kaasalainen, Jaakkola, Kaasalainen, Krooks & Kukko, 2011; Soudarissanane, Lindenberg & Menenti, 2009).
De esta manera, cuando se capturan datos sobre un escenario y se genera un modelo en 3D de las superficies (Al-Durgham, Habib & Kwak, 2013), estas mediciones son vulnerables a los efectos de ruido que se presentan en el montaje de un proyecto (Gressin, Mallet, Demantké & Da, 20l3), debido a muchos factores que pueden distorsionar las dimensiones de los objetos. Por ello, se propone el desarrollo de un modelo estadístico que incluya las variables de objetos o targets (Zhou, Cui & Yang 2009), distancia y ángulos de incidencia que pueden afectar la exactitud de los datos capturados dentro de la generación de modelos 3D (Lichti & Licht, 2006; Ramos et al., 2015), a partir de datos obtenidos de un TLS.
Esta investigación tiene como objetivo principal determinar un modelo estadístico que represente la precisión de los datos adquiridos por un TLS (Lohani & Sasidhaan, 2017) mediante la realización de pruebas de campo en diferentes escenarios donde deben interactuar las variables de distancia, ángulo de incidencia y objetivos o targets a escanear (Chiba & Masuda, 2016; López & Ruiz, 2011). Dicho objetivo se plantea con la intención de establecer los errores en medición que se tienen al implementar estas nuevas tecnologías que son de gran avance para el campo de la topografía (Barragán & Escobar, 2017). En la primera parte de este artículo se establece la metodología de la investigación en donde se define el diseño del experimento y los modelos estadísticos a implementar para obtener el mejor ajuste posible de datos que permita establecer la exactitud de las mediciones realizadas con el TLS Faro Focus 3D frente a las obtenidas por topografía convencional (Aoki, Aoki & Miyamoto, 2017; Masuda & Tanaka, 2010), a partir de los cuales se presentan los resultados y conclusiones obtenidas de la investigación, con la obtención del modelo estadístico estimado, validado e interpretado que se ajusta al objetivo principal de este estudio (Date, Yokoyama & Sugawara, 2018; Takai, Date & Kanai, 2013).
Construcción de la metodología
Diseño del experimento
Se plantea el desarrollo de un escenario, donde se pueda escanear una superficie en un rango de distancia visible de 0 m a 120 m, teniendo en cuenta las especificaciones técnicas del TLS Faro Focus 3D, para lo cual se definió una locación que cumplía con dicha condición dentro del campus de la Universidad Nacional de Colombia, en un costado del Estadio Alfonso López (foto 1).
Luego de establecer la zona de estudio (foto 2), se procede a diseñar la localización de cada uno de los puntos, sobre los cuales se tendrán en cuenta la variación de ángulos y distancias con relación a la superficie de captura. Para cumplir estas condiciones, se hace el diseño del esquema en oficina, de cada uno de los tres ejes con ángulos de 30°, 60° y 90° y distancias conocidas (figura 1). El diseño establecido se materializa en campo por medio de técnicas de levantamiento topográfico convencional, con una estación topográfica total, que hoy día es considerada una medición extremadamente confiable (Barragán & Martínez, 2015).
Cada uno de los puntos materializados en campo, es utilizado para ubicar sobre cada uno de ellos el TLS Faro Focus 3D, y realizar cada uno de los escaneos propuestos.
Diseño de objetos o targets de reconocimiento
Para la identificación de objetos dentro de los escaneos fue necesario diseñar una serie de targets u objetivos de reconocimiento para los escaneos (figura 2), los cuales fueron pensados para que se distinguieran en diversos colores, materiales, tamaños (véase tabla 1) y formas, que además fueran de fácil elaboración, accesibilidad a sus materias primas y representativos en los entornos naturales del espacio físico que tradicionalmente se documenta por medio del escáner terrestre.

Figura 2 Tipos de targets u objetos a ser escaneados. (a) Tipo 1, papel negro, (b) Tipo 2, madera variedad cedro, (c) Tipo 3, cinta reflectiva, (d) Tipo 4, Cartonplast blanco, (e) Tipo 5, Cartonplast rojo, (f) Tipo 6, papel brillante en aluminio, (g) Tipo 7, media esfera de poliestireno, (h) Tipo 8 papel brillante en aluminio con agujeros.
Implementación del diseño
En este proceso, el diseño del experimento definido en oficina se materializa en la práctica por medio del levantamiento topográfico convencional. Seguidamente, se realiza el escaneado de la superficie de estudio desde diferentes puntos localizados en campo (Theiler, Wegner & Schindler, 2013).
Levantamiento topográfico convencional
Este se realiza según lo presentado en la figura 1, donde a partir del diagrama de diseño se muestra la localización de cada uno de los puntos, donde se hará el levantamiento con el escáner terrestre. Puntos colocados sobre los tres alineamientos definidos (en ángulos de 30°, 60° y 90° con respecto a la superficie de escaneo). La localización precisa de dichos puntos en el terreno se realiza por medio de métodos de topografía convencional, con estación topográfica total (foto 3).
Tras la demarcación en campo con estacas de cada uno de los puntos sobre los cuales se hacen los escaneos, se elige el punto ubicado a 15.595 m de distancia en un ángulo perpendicular a la superficie de escaneo. Precisamente, como base para realizar el levantamiento topográfico de los elementos dentro de esa superficie, incluidos la cantidad de objetivos de escaneo por cada uno de los tipos targets, se distribuyen aleatoriamente a lo largo de la superficie, teniendo en cuenta que se cubra de manera equitativa la totalidad del área.
Este levantamiento topográfico sirve de insumo en el proceso de identificación y extracción de coordenadas de los targets, para realizar un análisis diferencial de la exactitud de los datos capturados por medio del TLS con relación a las coordenadas reales levantadas por topografía convencional.
Levantamiento TLS
El TLS Faro Focus 3D es un equipo que captura gran cantidad de puntos a alta velocidad, que facilitan la medición y la documentación aplicables a diferentes campos de ejecución. Por otro lado, la información resultante de un escaneo está formada por nubes de puntos, que representan una reproducción digital exacta de la realidad capturada en un corto lapso de tiempo (foto 4).
Para la captura de datos por medio del TLS Faro Focus 3D, enmarcado en el diseño del experimento planteado, se procede con la ubicación del equipo, en cada uno de los puntos y desde allí hacer el levantamiento con los siguientes parámetros de configuración por escaneo.
Si se incrementa el factor de calidad, se reduce el ruido en los datos y, por tanto, aumenta la calidad del escaneo, lo que se traduce en un aumento del tiempo de adquisición (véase tabla 2). Respecto al nivel de calidad aplicado a un escaneo, se hace con tasas de medición o aplicando compresión de ruido adicional (Wujanz, Burger & Mettenleiter, 2017).
Luego de la adquisición de datos capturados por el TLS Faro Focus 3D, estos deben administrarse y procesarse mediante el reconocimiento de objetos o targets establecidos en el experimento.
Resultados
Definición del modelo estadístico
Dentro de la especificación del modelo teórico se incluyen las variables protagonistas del desarrollo del mismo, las cuales se establecen como la distancia de escaneo (Ozendi, Akca & Topan, 2017), los targets u objetivos de reconocimiento del escaneo y los ángulo de incidencia propuestos (Soudarissanane, Lindenbergh & Menenti, 2011), que para el caso puntual de la modelación se van a tomar en sentido horario con respecto a la superficie de captura, por lo que equivaldría a hablar de ángulos de 60°, 90° y 150°, respectivamente, teniendo en cuenta el diagrama del diseño del experimento (Soudarissanane, Lindenbergh & Menenti, 2009).
En la búsqueda de un modelo estadístico, que explique el comportamiento de las observaciones obtenidas en campo de los targets levantados por medio de la topografía convencional y el TLS (Poreba & Goulette, 2015), se acudió a diferentes áreas de la estadística, entre las cuales se encuentran la geoestadística y los modelos lineales generalizados (MLG), siendo esta última la solución óptima para el fin del estudio. Por un lado, la geoestadística prometía ser una herramienta útil en la predicción del error obtenido al realizar las mediciones con el escáner láser, puesto que considera la correlación espacial que pueda existir entre las observaciones en un mismo escaneo; sin embargo, dichas predicciones tenían un horizonte de tan solo 20 metros y estaban limitadas al espacio donde se realizaron las medidas, el cual es bastante ideal; contrario al sinnúmero de configuraciones que pueden encontrarse en la práctica (Sumi, Date & Kanai, 2018).
A partir de los datos obtenidos en los diferentes escaneos realizados con el TLS y el del levantamiento por medio de topografía convencional con estación total, se hace un análisis estadístico diferencial que toma como reales las coordenadas obtenidas por este último levantamiento; es decir, como variable de referencia para hallar la exactitud de los errores en los datos obtenidos con el TLS (Yang, Dong & Liang, 2016). De lo anterior, se hace el cálculo de la distancia euclidiana (véase ecuación 1) donde se obtienen los valores de error para cada uno de los targets.
Donde la distancia euclidiana entre x, y, z está dada por la raíz de la suma del cuadrado de las diferencias de las variables de la función. El resultado de esta ecuación representa el error de los datos en la medición con el TLS para cada uno de los targets, y a partir de este valor se calculó la media por cada target dentro de cada uno de los escaneos, que de ahora en adelante será entendida como la variable de respuesta para el desarrollo del modelo estadístico por medio de la implementación de MLG.
Haciendo uso del postulado donde las mediciones obtenidas entre targets son independientes y, asimismo, entre los diferentes tipos de escaneo, se utilizó el análisis de MLG (López & Ruiz, 2011) para ajustar un modelo al error medio (media de las distancias euclidianas entre las coordenadas observadas y las teóricas) obtenido para cada escaneo en cada target (variable respuesta), teniendo como covariables el ángulo, la distancia y, claro está, el target (Yoshimura, Date & Kanai, 2016).
El proceso de estimación de parámetros se realiza calculando el valor de los coeficientes del modelo examinado a partir del conjunto de datos de las observaciones del error medio, para determinar si el modelo teórico propuesto es aceptable como una representación aproximada que se ajusta de la mejor forma a los datos (Dong, Cai & Du, 2016; Xu, Boerner & Yao, 2017).
Durante la evaluación del modelo, se examinan y se comprueban que las observaciones individuales cumplan los supuestos de normalidad, linealidad (Cohen, 1962), homocedasticidad (Little, 2013) e independencia, características del MLG (Enderlein, McCullagh & Nelder, 1987). A su vez, la validación del modelo se realiza a partir de los gráficos de bandas y el criterio de la distancia de Cook, donde se verifica el ajuste del modelo con los valores del error medio de las distancias euclidianas por target en cada uno de los escaneos.
Para la implementación del análisis por medio de MLG se usa el software libre R donde se realiza el desarrollo del modelo estadístico propuesto en la investigación. Mediante la teoría del diseño del experimento, las mediciones realizadas en cada uno de los escaneos son independientes entre sí (ejemplo: escaneo 2 es independiente de los escaneos 1, 3, 4, 5, 6, 7, 8 y 9), ya que fueron ejecutadas en diferentes ángulos y distancias con respecto a la superficie de captura. Adicional a esto, los datos obtenidos de los tipos de targets también cumplen con esta condición de independencia, pues las mediciones obtenidas para cada tipo target son independientes según el tipo de target (ejemplo: las medidas del target tipo l, son independientes a las medidas de los targets tipos 2, 3, 4, 5, 6, 7 y 8). Por lo que se propuso la implementación del análisis de MLG para ajustar un modelo al error medio (media de las distancias euclidianas entre las coordenadas observadas y las teóricas) obtenido para cada escaneo en cada target (variable respuesta), teniendo como covariables el ángulo, la distancia y, claro está, el target. Para la definición de la variable respuesta dentro del modelo, fue necesario descartar los escaneos 7 y 8, puesto que la resolución de estos era demasiada pobre y no se logró extraer información de coordenadas de los targets (Lu, Wang & Guo, 2018).
A partir de lo anterior se comenzó con la implementación del modelo en el software estadístico R, para lo cual se inició con la premisa de considerar que el error es una variable cuyo dominio son los reales positivos. Por lo que se propone un modelo de la familia de distribuciones Gamma para explicar el comportamiento de esta variable (Forstner & Khoshelham, 2017). Para verificar si la familia de distribuciones Gamma es adecuada para el ajuste del modelo, se emplean las estadísticas descriptivas (véase tabla 3).
De las estadísticas descriptivas del error medio, puede decirse que la variable respuesta es sesgada a la derecha (la media es mayor que la mediana). Para verificar este hecho e identificar la intensidad de dicho sesgo, se ilustra la densidad de la dicha variable respuesta (figura 3).
En la figura 3 se observa, a la derecha, un sesgo bastante pronunciado, razón por la cual se establece la familia de distribuciones Gamma para la estimación del modelo.
De los gráficos que se ilustran en las figuras 4 y 5, puede decirse que la dispersión no es constante entre las observaciones. Nótese que el error medio toma valores entre 0 y 0,15 aproximadamente, para todas las distancias medidas excepto para los 80 m donde se observa un posible dato atípico con un valor superior a 0,25 y una concentración de los puntos de cerca de 0 y 0,05. De manera análoga, en el gráfico de dispersión de los ángulos se nota la presencia de un posible valor atípico para los ángulos de 90° y 150°, y de nuevo (Ge, 2017) la dispersión de los puntos parece no ser homogénea entre ángulos. Por último, del box-plot en la figura 6, se observa que las cajas poseen anchos diferentes, lo cual indica que no existe la misma dispersión de las observaciones entre targets. Con base en lo anterior, se concluye que no es adecuado asumir una dispersión constante; por tal motivo, se decide ajustar un modelo lineal generalizado doble.
Densidad del error medio
Considerando que la dispersión de la respuesta es más notoria entre targets, se propone el siguiente modelo estadístico (véase ecuación 2).
Donde:
Con j = 1,…, 8
X 9k = Distancia de la k-ésima observación
X10k = Ángulo de la k-ésima observación
Yk = Error medio de la k—ésima observación
μk = Valor esperado poblacional de la k-ésima observación.
ϕk = Parámetro de dispersión asociado a la k-ésima observación.
ß j = Incremento o decremento en el error medio en el target j con respecto al target 1, para j = 2,..., 8
ß9 = Incremento o decremento del error medio por cada metro adicional
ß10 = Incremento o decremento del error medio por cada grado adicional
γ1 = Incremento o decremento en la dispersión porcada grado adicional
Para la identificación de las variables cuyo efecto es estadísticamente significativo sobre el error medio esperado se acudió al estadístico de Wald (Lemonte & Vanegas, 2005), el cual está dado por la siguiente expresión (véase ecuación 3).
Donde  y
y  corresponden a las estimaciones de ß
j y su error estándar asociado σ
j, esto para j = 2,...,10. El estadístico de Wald está asociado al sistema de hipótesis (véase ecuación 4).
corresponden a las estimaciones de ß
j y su error estándar asociado σ
j, esto para j = 2,...,10. El estadístico de Wald está asociado al sistema de hipótesis (véase ecuación 4).
Donde H0 es equivalente a decir que el efecto de la variable X j no es estadísticamente significativo sobre el error medio esperado.
La regla de decisión del sistema de hipótesis es:
Donde p-valor = 2*P(Tc >Tn-p ) n siendo el tamaño de muestra y p el número de parámetros del modelo.
De manera análoga, se tienen los sistemas de hipótesis asociados a los efectos de los γj sobre la dispersión, da dos por la siguiente expresión (véase ecuación 5).
Esto para j = 2,…,8.
Se obtiene que para una significancia del 1% la distancia es la única variable que tiene un efecto estadísticamente significativo sobre el error medio esperado con un p-valor = 0,000974. Por otro lado, se concluyó que el parámetro ϕk es constante para todo k; es decir, las covariables asociadas a los targets no tienen un efecto estadísticamente significativo sobre la dispersión. Por lo cual, el modelo final teórico queda definido como sigue (véase ecuación 6).
En la tabla 4 se ilustran los parámetros estimados, su error estándar y su p-valor asociado.
Nótese que el parámetro ß1 tiene un p-valor mayor al nivel de significancia del 1%; sin embargo, este se conserva por cuestiones de ajuste del modelo. Cabe resaltar que este no tiene interpretación práctica.
Reemplazando el valor de las estimaciones sobre el modelo propuesto, se obtiene el siguiente modelo estadístico final estimado (véase ecuación 7).
Validación del modelo
Para la validación del modelo se emplean los gráficos de bandas de 99% confianza y el criterio de la distancia de Cook para la identificación de observaciones potencialmente influyentes. Al observar las figuras 7 y 8 que ilustran las bandas de confianza, se encuentra que existen dos puntos fuera de estas (observaciones 19 y 18) para el modelo asociado a la media; sin embargo, esta distancia no es considerable y puede explicarse por la variación aleatoria de los datos. Por otro lado, para el modelo asociado a la dispersión se observa que no existe punto alguno fuera de las bandas, a partir de esto se concluye que el modelo se ajusta de forma adecuada. En los gráficos asociados a la distancia de Cook que se ilustran en las figuras 9 y 10, se tiene de nuevo que la observación 18 presenta valores posiblemente atípicos y en este caso especial potencialmente influyentes; a esto se le suma que las observaciones 15 y 23 también se postulan como potencialmente influyentes; sin embargo, al extraer estas observaciones y realizar el ajuste del modelo no se generan cambios estadísticamente significativos en el efecto de la distancia sobre el error medio esperado.

Figura 9 Distancia de Cook para el reconocimiento de observaciones potencialmente influyentes para la media

Figura 10 Distancia de Cook para el reconocimiento de observaciones potencialmente influyentes para la dispersión
Residuo componente del desvío para dispersión
Finalmente, como  puede concluirse que el error medio esperado aumentará un
puede concluirse que el error medio esperado aumentará un  por cada metro adicional en la distancia del escáner. Teniendo en cuenta que un intervalo del 99% de confianza para ß9 está dado por
por cada metro adicional en la distancia del escáner. Teniendo en cuenta que un intervalo del 99% de confianza para ß9 está dado por  es decir [0,00033, 0,015], al sacar el exponencial a los límites se tiene que el intervalo queda dado por [1,00033, 1,01515], a partir del cual se concluye que por cada metro adicional en la distancia del escáner el error medio esperado aumentará entre 0,033% y 1,5%.
es decir [0,00033, 0,015], al sacar el exponencial a los límites se tiene que el intervalo queda dado por [1,00033, 1,01515], a partir del cual se concluye que por cada metro adicional en la distancia del escáner el error medio esperado aumentará entre 0,033% y 1,5%.
Conclusiones
Es posible obtener un modelo con base en fundamentación estadística para determinar la exactitud de los datos adquiridos por medio de un TLS Faro Focus 3D, a partir del cual se estableció que por cada metro adicional en la distancia del escáner con relación a una superficie de estudio, el error medio esperado aumentará entre 0,033% y 1,5%.
Dentro de las especificaciones técnicas del equipo Faro Focus 3D, se describe de manera generalizada el error en las medidas del equipo como ± 2 mm por cada intervalo entre 10 m y 25 m limitando dicho error en un rango de distancia máxima de hasta 120 m. A partir del desarrollo del modelo con base en las pruebas de campo se pudo establecer que a una distancia de 120 m el error de medición que se puede tener es calculado entre 52,3 mm y 122,9 mm.
A partir del análisis estadístico en el desarrollo del modelo, se pudo establecer que de las variables o parámetros involucrados inicialmente, la distancia es la que mayor incidencia tiene sobre los errores que pueden presentarse en los datos adquiridos con el TLS. Pero, por otro lado, la variación de ángulos y targets no presenta gran significancia dentro de la exactitud de los datos al compararlos con los obtenidos por topografía convencional. Sin embargo, en las pruebas de campo realizadas para adquirir datos por medio del TLS Faro Focus 3D, se pudo observar que la resolución del escaneo o la cantidad de puntos capturados disminuye para la misma superficie de estudio, al aumentar la distancia y al hacer escaneos desde ángulos entre dos rangos aproximados, el primero de 0° a 60° y el segundo de 120° a 180° si se toman los ángulos en sentido horario con relación a la superficie de captura.
Teniendo en cuenta la variable respuesta introducida en el modelo como la media de las distancias euclidianas entre las coordenadas observadas y las teóricas, se pudo establecer que el tipo de target que arroja mejor exactitud es el tipo 2 que corresponde con madera tipo cedro y, por el contrario, el que más error presenta es el tipo 6, hecho de papel brillante.
En el diseño del experimento se planeó comparar dos escaneos realizados desde un mismo punto mediante el TLS Faro Focus 3D, pero configurado con diferentes parámetros de calidad, como en el caso de los escaneos 8 y 9, tomados a 120 m a un ángulo de 90° con una resolución de 1/2 y variando el factor de calidad por 4x y 6x, respectivamente. Se pudo validar que el parámetro de calidad del TLS está relacionado con la reducción del ruido en los datos de escaneo, lo cual hace que el tiempo de captura se incremente y que exista gran pérdida de información, caso que no fue conveniente en esta investigación. Como consecuencia de ello, el escaneo 9 capturado con factor de calidad 6x, se descartó en la modelación estadística de los datos.
Recomendaciones
Teniendo en cuenta que, en el resultado de la implementación del modelo, se obtuvo que las variables de ángulo de incidencia y target no presentan una afectación significativa dentro de la exactitud de los datos adquiridos con el TLS Faro Focus 3D, sería un gran aporte realizar una investigación donde se pueda establecer la posible relación de estas dos variables con relación a la resolución del escaneo, es decir, si de estas depende la cantidad de puntos capturados en un escaneo.
El modelo estadístico generado aquí, se realizó teniendo en cuenta los errores medios de las distancias euclidianas entre el levantamiento topográfico con estación y el levantamiento por medio del TLS Faro Focus 3D, estableciendo para cada uno de esos errores una configuración de los parámetros de distancia, ángulo de incidencia y target. Si se quieren obtener los rangos de error para otro tipo de TLS, sería recomendable validar, por medio de los procedimientos plasmados en este trabajo, el ajuste de dichos datos al planteamiento de este modelo.