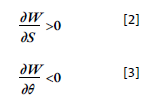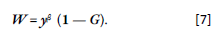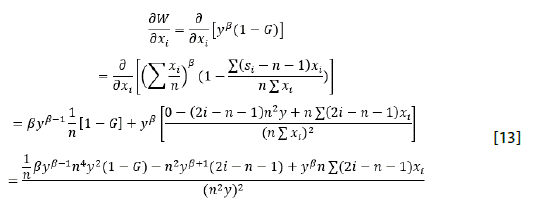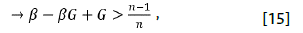La relación generalizable entre desigualdad, bienestar e ingreso

Desde su origen en Bergson (1938), la SWF ha evolucionado significativamente dentro de la teoría económica, la cual ha tenido puntos de discusión interesantes sobre el debate de equidad y eficiencia. Tal y como lo menciona Mukhopadhaya (2003a) en la práctica, la función se utiliza en la consideración de impactos distributivos para la sociedad en relación con el análisis de la disyuntiva de eficiencia y equidad en el bienestar social. La SWF abreviada se representa en su aproximación más simple como:

donde W es el nivel de bienestar social, S y θ son funciones del perfil de ingresos x de la sociedad. La característica de S en la ecuación 1 es que es una representación del ingreso total de la sociedad, el cual busca capturar el aspecto de eficiencia en la economía. Por otro lado, θ representa el nivel de desigualdad enmarcado en la sociedad y busca capturar el aspecto de equidad en el análisis.

Las propiedades de la función 1 deben satisfacer:

Es decir, la SWF de la ecuación [¹] debe ser creciente respecto al perfil de ingresos de la sociedad, y decreciente en relación con el nivel de desigualdad. Además de esto impondremos que [¹] debe ser cóncava para reflejar el criterio de preferencia por la equidad necesario en el análisis. Mukhopadhaya (2003a) en este punto indica que la preferencia por la equidad está dada al existir una transferencia del ingreso de una persona con alto nivel de ingreso hacia una con bajo nivel; dicha transferencia mejora el nivel de bienestar social considerablemente.

La función de la ecuación 1 también tiene que estar acorde con el principio de Pareto en el cual, si hay un incremento en el ingreso de una persona, con todas las demás variables constantes, el nivel de bienestar aumentará. Simbólicamente esto está expresado como:

Aquí se refiere al nivel de ingreso del individuo considerando individuos en la población. La relación de [⁴] indica una variación positiva del nivel de bienestar social ante la variación positiva del nivel de ingreso del individuo sin importar su posicionamiento o nivel de ingresos.

Sen (1974) asume que la utilidad marginal de la sociedad en su conjunto está inversamente relacionada con su posicionamiento en la distribución del ingreso. Esto implica que, las transferencias de ingreso entre el grupo poblacional con mayores ingresos hacia el grupo poblacional con menores ingresos, incrementa de forma general el nivel de bienestar de la sociedad. Esta perspectiva, permite la introducción axiomática desde la visión de Sen de la SWF que se define como:

Donde y es el ingreso medio de la sociedad y G es el coeficiente de Gini en la distribución del ingreso. La SWF en [⁵] es la llamada función de bienestar social de Sen y cumple con las condiciones [²] y [³]. El índice de Gini en este contexto considera el ordenamiento por percentiles poblacionales en relación con la distribución general del ingreso de la economía, lo que satisface la condición de incrementos en la utilidad marginal de la sociedad respecto a transferencias del ingreso considerando la ubicación de grupos poblacionales ordenados.

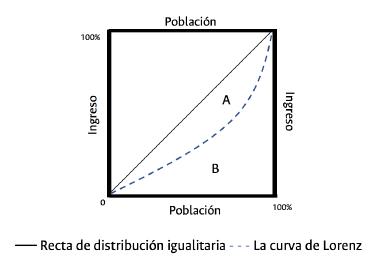
El coeficiente de Gini, se define como el doble del área que comprende la línea de distribución igualitaria (45° grados) y la curva de Lorenz. La mencionada área está demarcada en la figura 1, como el punto A. Por esta razón, el complemento del coeficiente de Gini (1 - G) se representa como el doble del área B que se define a partir del área debajo de la curva de Lorenz.

Fuente: elaboración propia.

Figura 1 Curva de Lorenz 

La inferencia de lo anterior es que, a mayores niveles de concentración del ingreso, existe una disminución del bienestar general de la sociedad -desde la expresión de la SWF de Sen-, debido a que, el doble del área de B -es decir 1 - G denominado complemento de Gini- se reduce paulatinamente a medida que el área demarcada en A aumenta. La tasa de sustitución entre desigualdad y eficiencia en el contexto de la SWF de Sen está dada como:

Por [⁶] se destaca que la tasa de sustitución es altamente sensible a los cambios en el ingreso y, a diferencia de los cambios en el nivel de desigualdad G, considerando que estas dos variables están determinadas por el perfil de ingresos x de la sociedad.

Una discusión importante emerge en este punto. Mukhopadhaya (2003a) argumenta que tanto G como y están determinados y -por lo tanto- el agente decisor dentro de la economía no puede cambiar o alterar estas variables para diferentes niveles de crecimiento económico o del ordenamiento en la distribución del ingreso. Sin embargo, este aspecto puede ser discutido en más de un sentido. Para empezar, el Estado y la administración pública juegan un rol importante en el proceso de redistribución del ingreso, afectando directamente los niveles de desigualdad económica (Tomaszewicz & Trębska, 2015) y desarrollo económico (Gründler & Köllner, 2017). En este sentido, Zhang (2007) advierte que no solo son los canales de gasto público o transferencias gubernamentales los que influyen en los niveles de desigualdad, sino también los procesos de inversión pública -en especial los focalizados a educación- que afectan los niveles de concentración del ingreso y en general el patrón de desarrollo de una economía.

Por ende, se argumenta que el valor de G puede ser variante en el tiempo a partir del conjunto de decisiones de políticas distributivas de las economías que los gobiernos implementen y hagan efectivas. En este sentido, el proceso de redistribución del ingreso juega un rol imperante en las mejoras agregadas del bienestar, teniendo una estrecha vinculación con las decisiones de política económica, aunque con menor impacto que el crecimiento económico dada la tasa de sustitución en [⁶].

La formulación de Sen basada en la expresión 5 indica que su formulación se puede interpretar como una función paretiana extrema² de bienestar social (Mukhopadhaya, 2003b) e intenta cubrir las deficiencias de la curva de Lorenz, dado que permite estimar la tendencia general de bienestar desde sus componentes de eficiencia y equidad (Ndamsa et al., 2020).

El proceso de generalización de la SWF de Sen surge como una crítica al estricto cumplimiento del principio de Pareto, dicha generalización la propone Mukhopadhaya³ (2003a) y es definida a partir del planteamiento:

Nótese que si β < 1, la SWF deja de tener un comportamiento basado en el principio de Pareto definido en [⁴] y esto se explica en el teorema número 1 de Mukhopadhaya (2003a), que se encuentra desarrollado en el anexo A. La justificación es que no todos los cambios positivos en el ingreso de todos los grupos poblacionales incrementan de la misma manera el bienestar social agregado, la crítica es que el criterio del principio Pareto puede no aplicar para los percentiles poblacionales que tienen la mayor cantidad de ingresos. En este sentido, variaciones positivas del ingreso en este percentil poblacional, puede tener un efecto nulo o incluso negativo en el bienestar social agregado y, por ende, no es aplicable el principio de Pareto representado en [⁴]. Siempre que β < 1, la función deja de regirse por el principio mencionado; esta perspectiva es compartida por Baluch & Razi (2007), enfatizando que las variaciones positivas en los grupos poblacionales de mayores ingresos no siempre traen consigo variaciones positivas en los niveles de bienestar social agregado. Aquí es de destacarse que cuando la SWF generalizada de [⁷] tiene un valor de β = 1, la resultante será la formulación original de Sen (1974), expresada en la ecuación 5.

Aspectos metodológicos

Estimación tradicional de la SWF

A partir del apartado anterior, existen dos funciones que nacen desde la perspectiva de Sen: en primera medida, la tradicional función consignada en la ecuación 5 y, en segunda medida, su forma generalizada propuesta por Mukhopadhaya (2003a), representada en la ecuación 7. En este apartado, se discuten las formas de estimación de ambas.

De forma general, considerando una periodicidad anual entre 1995 y 2018 para 15 países de América Latina⁴, se propone la estimación de la función original de bienestar social planteada en Sen (1974) de la forma:

donde representa el subíndice asociado a un determinado país, y hace referencia al tiempo - en forma anual-. Bajo esta perspectiva, W es sencillamente el cálculo resultante del producto del ingreso medio de la sociedad y, asumido como el PIB per cápita real en moneda común para todos los países, y el complemento del coeficiente de Gini (1 - G ). Esta aproximación se utiliza con fines comparativos (Baluch & Razi, 2007; Mukhopadhaya, 2003a; Sen, 1976) en harás de determinar cuantitativamente la tendencia de bienestar agregado por país.

En segundo lugar, con el uso de la función generalizada de Sen desarrollada por Mukhopadhaya (2003a) de la forma:

El cálculo puede realizarse asumiendo valores constantes de i, en virtud de establecer diferencias cuantitativas en los niveles de bienestar social de las economías bajo la óptica que rechaza el principio paretiano en la función de Sen. Según el estudio de Mukhopadhaya (2003b), usar un valor constante como β= 0.5, permite identificar una diferencia destacable con la función original de Sen sin generalizar, diferencia que surge en las comparaciones y posicionamiento entre los niveles de bienestar⁵. Hasta este punto, bajo el enfoque original de la SWF de Sen, se asume que el bienestar social W es desconocido y solo es medible a través de la expresión del ingreso medio junto con el coeficiente de Gini G.

En este artículo se propone la posibilidad de usar una variable proxy que capture la esencia de W en virtud de determinar econométricamente el valor de fi, lo cual es una aproximación más realista que asumir que la elasticidad del bienestar-ingreso es constante en todos los periodos de tiempo para los países de análisis. La elección de una variable como medición del bienestar ha sido debatida ampliamente en la literatura y teoría económica (Anand & Harris, 1994). Sin embargo, aquí se considera el indicador sintético propuesto por el Programa de las Naciones Unidas para el Desarrollo (PNUD) denominado Índice de Desarrollo Humano (IDH). Esta variable compone rasgos importantes capturados por las dimensiones de salud, educación y el nivel de vida digno que inciden directamente en el nivel de bienestar para los habitantes de una economía (PNUD, 2019). De hecho, tal y como lo proponen Sen (1974) y Mukhopadhaya (2003a) desde la SWF, el énfasis del bienestar tiende a estar principalmente explicado por el nivel de ingreso en la determinación del bienestar W, el cual es un componente principal en la construcción del IDH, pero no determinado únicamente por este mismo, sino en conjunto con los demás componentes relacionados con la salud y el conocimiento que constituyen factores esenciales en los niveles de bienestar de la población de cada país.

Estimación econométrica

De la función de bienestar social generalizada de la ecuación [⁹], se propone que representa la elasticidad bienestar-ingreso en la formulación teórica de Sen, así mismo el complemento del coeficiente de Gini se le puede asignar como exponente un parámetro de elasticidad en relación con el nivel de bienestar, junto a esto se considera que existe un parámetro autónomo de bienestar independiente del ingreso y de la desigualdad, así como la especificación de un componente de efectos fijos individuales para capturar la heterogeneidad individual de los países. De esta forma que el modelo es especificado como:

donde W _it representa el nivel de bienestar social del país i en el año t medido por el IDH.y _it es el ingreso medio medido por el PIB per cápita en términos reales en moneda común, β ₁ es la elasticidad bienestar-ingreso, G es el coeficiente de Gini, α es la elasticidad asociada al bienestar desde el complemento del coeficiente de Gini (1 - G), β ₀ es el coeficiente autónomo e independiente del ingreso y el nivel de desigualdad, p es el componente de efectos fijos individuales que captura la heterogeneidad individual (Wooldridge, 2001) existente entre los países de América latina y u _it el residual de la regresión de panel datos.

La linealización de esta función anterior utilizando logaritmos naturales se presenta como modelo econométrico propuesto para ejecutar la estimación de la forma:

Al tener un panel de datos con T>N y considerando las características del conjunto de variables en el modelo econométrico planteado en [¹¹], es posible segmentar también los análisis de corto y largo plazo bajo la metodología de Engle y Granger (1987) y extender el análisis a la cointegración de paneles (McCoskey & Kao, 1998). De hecho, la ecuación [¹¹] -al tener solamente valores contemporáneos en el tiempo- se puede entender como la relación de largo plazo entre las variables de análisis, que se encuentran con la característica de poseer raíces unitarias en niveles pero estacionarias en primeras diferencias, definiendo un conjunto de acuerdo con las pruebas de raíces unitarias de primera y segunda generación (véase anexo B).

Para el análisis de cointegración entre las variables -extendido a la aplicación en panel de datos- se necesita de la generación de un modelo de corrección del error, donde primero se verifica la existencia de cointegración en la relación de largo plazo de la ecuación [¹¹] por pruebas específicas para confirmar la cointegración de datos de panel (Kao, 1999; Pedroni, 1999) y, después de comprobarse, se plantea un modelo de corrección del error utilizando las variaciones de la relación de largo plazo -entendidas como primeras diferencias- y la información de la relación de largo plazo en un término de corrección del error, derivando en el modelo de corto plazo de la forma:

donde Δ es el operador de primeras diferencias. El término de corrección del error es definido como ECT _it-1 =û _t1 . Es decir, es una variable que contiene los valores rezagados de los residuales estimados de la ecuación de largo plazo de [¹¹]. El parámetro asociado al largo plazo, φ, como término de corrección del error debe ser negativo, entre 0 y 1, y significativo estadísticamente para indicar que el proceso de ajuste hacia el equilibrio en la relación de largo plazo es estable.

Considerando que el panel es T>N, la relación de largo plazo en [¹¹] y de corto plazo en [¹²] son susceptibles de tener problemas de heterocedasticidad, autocorrelación y dependencia de corte transversal. Para evitar una inferencia errónea en términos de significancia estadística, el estimador propuesto para las regresiones es el formulado por Driscoll y Kraay (1998) el cual presenta errores estándar robustos a los problemas de autocorrelación serial en el tiempo, heterocedasticidad en los residuales y la dependencia de corte transversal en la regresión multivariada, ideal para los paneles de mayor o igual cantidad de puntos temporales en comparación con el conjunto de individuos de la muestra (Hoechle, 2007).

A través de esto, las relaciones de corto y largo plazo entre bienestar, ingreso y desigualdad pueden estimarse para los países de América Latina entre el periodo de 1995 y 2018. Las fuentes de información de las variables -PIB per cápita en dólares a precios constantes de 2010 y el coeficiente de Gini- para los diferentes países de América Latina fueron tomadas del Banco Mundial (s. f.) y la información del IDH fue tomada del PNUD (s. f.).

Resultados de la estimación tradicional

Los resultados empíricos considerando la función SWF original de Amartya Sen (1974) para América Latina se presentan en la figura 1, donde se recalca que aquí el parámetro de elasticidad bienestar-ingreso es β = 1.

Fuente: elaboración propia con datos del Banco Mundial (s. f.).

Figura 1 Estimación SWF original de Sen (1974) por país (β = 1 ) 

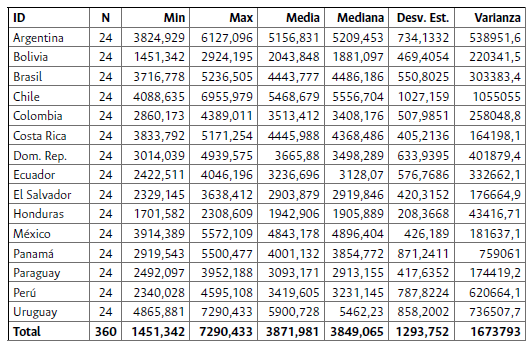
Se destaca que -para la generalidad de los países- la tendencia es creciente en los niveles de bienestar desde la SWF original de Sen. De manera puntual, Uruguay y Chile son los países que poseen los mejores niveles de bienestar, mientras que Bolivia y Honduras, son los que menor nivel poseen a lo largo del tiempo. Para el 2018, el ranking de países con mayores niveles de bienestar desde esta óptica es: 1) Uruguay, 2) Chile, 3) Panamá, 4) Argentina, 5) México, 6) Costa Rica, 7) Brasil, 8) República Dominicana, 9) Colombia, 10) Perú, 11) Paraguay, 12) Ecuador, 13) El Salvador, 14) Bolivia y 15) Honduras. Las estadísticas descriptivas del bienestar social calculado desde esta perspectiva se presentan en la tabla 1:

Tabla 1 Estadísticas descriptivas del bienestar agregado de la SWF Original de Sen (1974) 

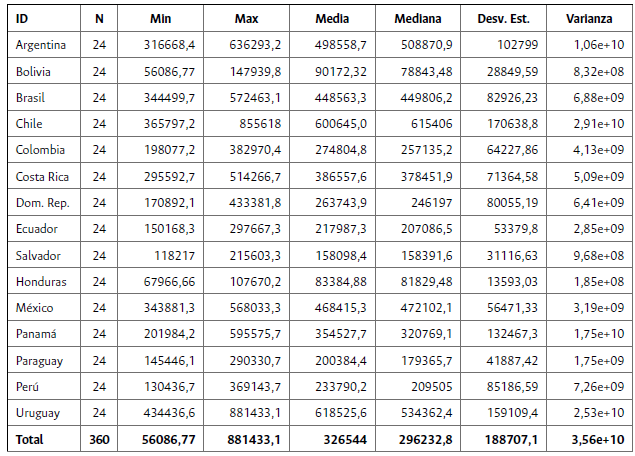
Fuente: elaboración propia.

Prosiguiendo con la estimación de la SWF con la versión generalizada propuesta por Mukho-padhaya con -el caso de la SWF donde no cumple el principio de Pareto- la tendencia de bienestar se presenta la figura 2.

Fuente: elaboración propia.

Figura 2 SWF generalizada estimada con β = 0.5 

Se destaca que existen unas ligeras variaciones en los cálculos de bienestar social agregado por país en comparación con la SWF original de Sen (1974). Asimismo, existe una leve reducción de brechas con el cálculo de la SWF generalizada. El aspecto tendencial del bienestar es positivo para América Latina igual que en la versión de Sen, pero también existe un cambio el ranking de países con mayor bienestar para el año 2018. El ranking tiene el siguiente orden: 1) Uruguay, 2) Chile, 3) Argentina, 4) México, 5) Panamá, 6) Costa Rica, 7) República Dominicana, 8) Brasil, 9) Perú, 10) Colombia, 11) Paraguay, 12) Ecuador, 13) El Salvador, 14) Bolivia, 15) Honduras.

Igual que en el análisis empírico de Mukhopadhaya (2003a), la posición de cada país varía para ciertos países cuando se considera el planteamiento original de la SWF como su versión generalizada. En América Latina -desde la versión generalizada- Panamá desciende y ocupa el quinto puesto, Argentina sube al tercer lugar y México al cuarto lugar. Brasil -en cambio- baja al octavo puesto junto con Colombia, que desciende al décimo puesto. Esta situación indica la existencia de ligeras variaciones en las medidas del bienestar a raíz de cambios en la elasticidad bienestar-ingreso asumidas en el parámetro . Las estadísticas descriptivas del bienestar calculado por la versión generalizada asumiendo se presentan en la tabla 2:

Tabla 2 Estadísticas descriptivas de bienestar social de la SWF generalizada con β = 0.5 

Fuente: elaboración propia.

Resultados de la estimación econométrica

Los resultados del análisis de raíces unitarias (véase anexo B) a través de las pruebas de primera y segunda generación de Levin et al. (2002) e Im et al. (2003) indican que el conjunto de variables del modelo de largo plazo poseen raíces unitarias en niveles, mientras que son estacionarias en primeras diferencias, confirmando su orden de integración requisito necesario para proseguir con el análisis de cointegración.

Las pruebas formales de cointegración de Pedroni (1999) y Kao (1999) -véase anexo C- reflejan evidencia de cointegración entre las variables propuestas para la estimación econométrica de la ecuación de largo plazo. Los resultados de la regresión con el estimador Driscoll-Kraay se presentan en la tabla 3.

Tabla 3 Regresión de la ecuación de largo plazo 

Nota: los logaritmos naturales del IDH, complemento del coeficiente de Gini y la constante están definidos como ln IDH, ln ( 1 - G ) y β ₀ respectivamente. Errores estándar robustos en paréntesis, niveles de significancia del ^*** p<0,01, ^** p<0,05, ^* p<0,1. Estimador utilizado Driscoll-Kraay. Cálculos realizados usando el programa Stata 16.

Fuente: elaboración propia.

Sobre la revisión de supuestos de la ecuación de largo plazo (véase anexo D), la regresión cumple satisfactoriamente los supuestos de no multicolinealidad, normalidad, y especificación correcta. Sin embargo, presenta la existencia de heterocedasticidad y autocorrelación⁶, problemas que son capturados por el estimador Driscoll-Kraay para proveer inferencias robustas.

Los resultados de la regresión se consideran consistentes al existir una relación de largo plazo establecida por las pruebas de cointegración en el panel de datos (Madsen, 2005), e indican que el PIB per cápita y el complemento del coeficiente de Gini son significativos al 1% para explicar el bienestar medido por el IDH. Los impactos de ambas variables sobre el bienestar son positivos. Se destaca que la elasticidad bienestar-ingreso (β = 0,174) es menor que la elasticidad del bienestar asociada al complemento del coeficiente de Gini (α = 0,184), situación que pone en evidencia que las mejoras del bienestar para América Latina se encuentran influenciadas -principalmente- por la reducción en la concentración del ingreso y en -segunda medida- por el incremento del ingreso per cápita. Lo anterior, considerando que el impacto de los estimadores refleja que por cada 1% que aumente el ingreso per cápita, existe un incremento del 0,17% en promedio entre los países sobre el IDH -ceteris paribus- significativo al 1%, consolidando un impacto inelástico sobre el bienestar. Asimismo, por cada 1% que aumente el complemento del coeficiente de Gini, existe un incremento del 0,18% en promedio entre los países sobre el IDH, ceteris paribus significativo al 1%, conformado también un impacto inelástico sobre el bienestar.

La estimación de corto plazo se presenta en la tabla 4 y se destaca que posee un coeficiente de ajuste de largo plazo negativo, significativo estadísticamente al 1%, con un parámetro entre cero y uno, expresando estabilidad hacia la relación de largo plazo estimada anteriormente. Los resultados indican que la velocidad de ajuste hacia la relación de largo plazo desde esta aproximación de corto plazo es alrededor del 9,64% de corrección anual entre las variables de análisis.

Tabla 4 Regresión de la ecuación de corto plazo 

Nota: A es el operador de primeras diferencias, ECT _t es el término de corrección del error. Niveles de significancia estadística dados por ^*** p<0,01, ^** p<0,05, ^* p<0,1. Estimador utilizado Driscoll-Kraay.

Fuente: elaboración propia.

Para el caso de la relación de corto plazo, se evidencia que solamente la tasa de crecimiento del PIB per cápita es significativa al 1% para explicar el crecimiento en el IDH, mientras que la tasa de crecimiento del complemento del coeficiente de Gini no es significativa al 10% para explicar el bienestar. En el caso del PIB per cápita, la elasticidad en el corto plazo indica que por cada 1% que aumente la tasa de crecimiento en esta variable, existe un impacto del 0,06% de crecimiento en el IDH -ceterts partbus- en promedio en los países de análisis. Dado que el complemento del coeficiente de Gini no es estadísticamente significativo para explicar las variaciones del IDH en el corto plazo, se concluye que las modificaciones en la concentración del ingreso no tienen impactos en el corto plazo, mientras que en el largo plazo tienden a ser determinantes -incluso con mayor impacto que el ingreso-en las mejoras en el bienestar social para los países de análisis de América Latina.

La revisión de supuestos de la relación de corto plazo (véase anexo D) es satisfactoria, el modelo, aunque posee heterocedasticidad -esto corregido por el estimador Driscoll-Kraay- cumple los supuestos de normalidad, no multicolinealidad, no autocorrelación serial y especificación correcta, por lo que la inferencia de los estimadores es robusta en las relaciones de corto y largo plazo.

Como ejercicio empírico final, a partir de la regresión de la relación de largo plazo, se presenta la predicción lineal en el periodo de tiempo dentro de la muestra -técnica conocida como In-sample Forecast- para corroborar el comportamiento de las tendencias de bienestar y las diferencias existentes en el posicionamiento de países en relación con sus niveles para América Latina. Los resultados generales se presentan en la figura 3 y el posicionamiento comparativo para 2018 en América Latina con las diversas estimaciones se presentan en la tabla 5.

Nota: el modelo utilizado para la predicción in-sample es la ecuación de largo plazo estimada en la tabla 3. Fuente: elaboración propia.

Figura 3 Resultados de la predicción lineal de la relación de largo plazo 

Se destaca que el comportamiento de la predicción del IDH de la ecuación de largo plazo en relación con la tendencia y el posicionamiento del bienestar social de los diferentes países de América Latina es muy similar a los resultados tanto de la versión original de la SWF de Sen como de su versión generalizada propuesta por Mukhopadhaya.

Tabla 5 Ranking de países por medición del bienestar social para el 2018 

Fuente: elaboración propia.

El posicionamiento de países por los niveles de bienestar desde la predicción lineal estimada econométricamente coincide exactamente con el posicionamiento de los países realizados a través del cálculo de la SWF original de Amartya Sen en el 2018. En este sentido, se destaca que la construcción teórica de Sen (1974; 1976) es un instrumento robusto para la aproximación y posicionamiento del bienestar social pese a estar representado principalmente por una expresión del ingreso medio de los países. Sin embargo, es de aclarar que la SWF de Sen y su versión generalizada, sirven para establecer comparaciones de los niveles de bienestar, más no para indicar una variable absoluta de medición integral del mismo. Los resultados econométricos dan evidencia de que el IDH puede ser utilizado como una variable de análisis del bienestar social, el cual -en términos de comportamiento de tendencia y posicionamiento- coincide con la aplicación empírica de la formulación teórica de la SWF propuesta por Sen (1974) en virtud de establecer los niveles de bienestar.