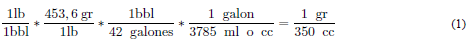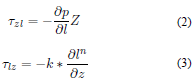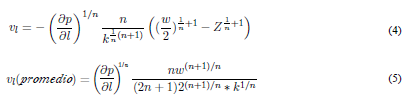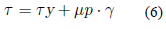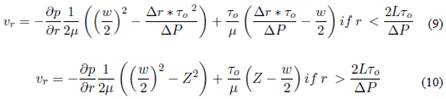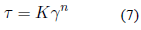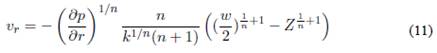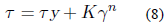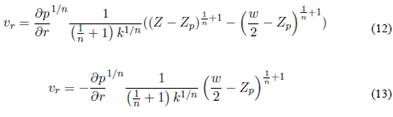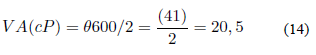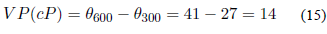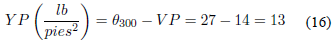Introducción
Evaluar y perforar formaciones complejas con presencia de fracturas y continuar desarrollando campos maduros con zonas de baja presión, favorece las pérdidas de fluido, lo que incrementa los Tiempos No Productivos (NPT). Siendo esta, la causa principal de problemas durante la perforación (Moazzeni et al., 2011; Avila-Parra y Ramirez-Boada, 2019). Se han propuesto métodos para estudiar el fenómeno de pérdidas de fluido a través de formaciones fracturadas, analizando la interacción entre el fluido de perforación y la cara de pozo (Xia et al., 2015a; 2015b).
Las fracturas naturales pueden tener efecto positivo o negativo sobre el flujo de fluidos. Por ejemplo, puede ser positivo para el flujo de aceite, pero negativo por el efecto de conificación del agua. Todos los yacimientos de hidrocarburos, son afectados de alguna manera por las fracturas naturales (Bratton et al., 2006). Los factores que influyen en estas fracturas y determinan su aporte durante la producción de hidrocarburos, y productividad son principalmente la densidad, ancho y diferencial de presión, estas dos últimas serán analizadas en esta investigación.
Debido al alto impacto que generan las pérdidas por circulación en términos de costos y estabilidad del pozo, algunos autores proponen modelos numéricos para caracterizar las fracturas conectadas por la broca, modelando el fenómeno de acuerdo con los datos de pérdidas de circulación registrados en campo. Sanfillippo et al. (1997) analizan el ancho de fractura y la permeabilidad respecto de un fluido newtoniano. Lietard et al. (1996) estudiaron el fenómeno de pérdidas usando reología de plástico de Bingham. Posteriormente, Lavrov y Tronvoll (2004) desarrollaron un modelo matemático para estudiar la presión del fluido de formación, la extensión y el ancho de la fractura, considerando factores operativos como el peso del lodo, la reología y el diámetro del pozo; este modelo se basa en la ecuación del momento y el comportamiento de la ley de potencia. Lavrov y Tronvoll (2005), analizaron nuevamente el fenómeno, utilizando un modelo analítico, estudiando dos tipos de reologías: newtoniana y no newtoniana. Finalmente, Vargas et al. (2019) modela el fenómeno de pérdidas incluyendo el efecto de la zona permeable, lo que aumenta la precisión del resultado.
Para entender el fenómeno, se propone una metodología que tiene dos componentes. Primero, la elaboración de un modelo físico a nivel de laboratorio. Segundo, la implementación de un modelo matemático que parte del balance de ecuación de movimiento y reología de la ley de potencia, que permite determinar el perfil de velocidad y la velocidad promedio de flujo a través de fracturas. Combinando estos dos ítems (modelo físico y modelo matemático) se logra comprender la interacción entre fluido de perforación y fracturas, estableciendo que el principal factor que afecta las pérdidas de fluido está asociado a la geometría de la fractura y a las propiedades reológicas.
Conceptos
Teoría de escalado
Las propiedades físicas de los materiales no se comportan proporcionalmente ante un cambio en sus dimensiones, por lo tanto, cuando se da un aumento en el tamaño de un cuerpo estas propiedades aumentan de manera diferencial; el área aumenta al cuadrado, el volumen, la masa y el peso aumentan al cubo y la presión se mantiene lineal, por su parte la gravedad y la densidad del lodo de perforación se mantienen constantes. A través de la teoría de similaridad, se escala el modelo análogo de manera correcta, relacionando parámetros entre el modelo análogo y el prototipo natural (Hubbert, 1937).
En el modelo físico las variables constantes serán la presión, gravedad y densidad del lodo de perforación. Para el caso de la densidad al preparar el lodo en el laboratorio, se determina las libras por barril equivalente para poder escalar de campo a laboratorio (Ecuación 1).
Concluyendo que una libra por barril en campo equivale a 1 gramo por centímetro cúbico en laboratorio. Luego de las pruebas de laboratorio los resultados de densidad se pasan a kg/m3 multiplicando por 1000, ya que los cálculos se realizan en el sistema internacional.
Modelos Reológicos y perfil de velocidad
Para analizar las pérdidas de fluido a través de zonas fracturadas, es necesario conocer con que velocidad se puede mover el fluido, en medio de dos placas que simulan la pared de la fractura. Para calcular esta velocidad, hay que recurrir a los modelos reológicos, los cuales consisten en el estudio de los principios físicos, que regulan el movimiento y la deformación de la materia, cuando es sometida a esfuerzos externos.
Los modelos varían según la relación entre el esfuerzo y velocidad de corte como se detalla en las ecuaciones 6, 7 y 8 explicadas en la Tabla 1.
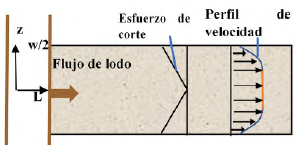
Para estimar el perfil de velocidad de fluido a través de la fractura, se inicia con el balance de la ecuación de movimiento (Ecuación 2) y el esfuerzo de corte se iguala al modelo reológico que satisface el comportamiento del fluido de perforación. Para el caso de estudio corresponde a la ley de potencia (Ecuación 3) En la Figura 1 se observan un comportamiento típico de un perfil de velocidad.
Luego de igualar las ecuaciones 2 y 3, integrar y despejar se obtiene velocidad en la ecuación 4 y la velocidad promedio ecuación 5
El procedimiento de la ecuación 2 a la 5 se aplica a los demás modelos reológicos con el fin de determinar las ecuaciones de velocidad, los cuales se resumen en la Tabla 1.
Tabla 1. Modelos reológicos principales.
Donde w es el ancho de fractura en metros (m), n es el índice de comportamiento de fluido (adimensional), z es la variación del espesor de fractura en metros (m), To es el esfuerzo de corte inicial en pascales (Pas) y v t es la velocidad en metros por segundo (m/s).
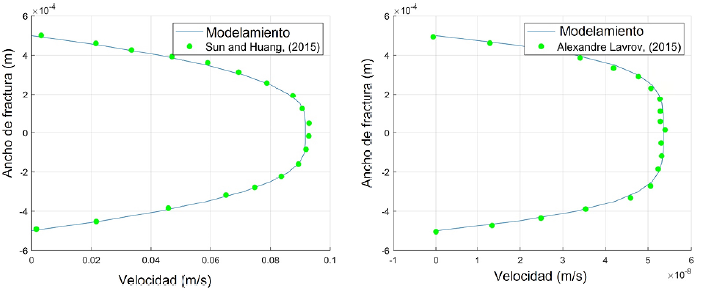
Luego de generar los modelos, el siguiente paso es la validación, para ello se toman los datos publicados de la Tabla 2.
Tabla 2 Datos para validar el modelo numérico.
| Reología | K pas*sn | n | To(Pas*s) | W (m) | ΔP | Referencia |
|---|---|---|---|---|---|---|
| Herschel-Bulkley | 0,2231 | 0,7 | 2,5 | 0,001 | 40-60-80-100 kPas/m | Sun y Huang (2015) |
| Ley de potencia | 0,005 | 0,3 | N. A | 0,001 | 1-5-75 Pas/m | Lavrov (2015) |
En la Figura 2 se resalta la precisión y confiabilidad del modelo implementado ya que presenta un error cercano a cero. Con el perfil de velocidad y el tiempo de exposición se calcula el volumen acumulado de fluido que pasa a través de la fractura y se compara con los resultados del modelo físico.
Metodología
Fase de diseño
Basado en el trabajo de maestría desarrollado por Uribe-Joya y Vargas-Silva (2023), quienes toman una muestra de la Formación Los Santos, de la zona norte de la Mesa de Los Santos. La muestra pertenece al Miembro Inferior de la formación que comúnmente se describe como de grano fino a muy grueso, tiene un alto contenido de matriz arcillo-arenosa que reduce significativamente la permeabilidad por tanto no hay pérdidas por filtrado durante el experimento. Tiene 5% de porosidad intergranular primaria asociada a microporosidad de la matriz y porosidad secundaria inferior al 10% asociado a microfracturas. A continuación, se detalla el procedimiento experimental.
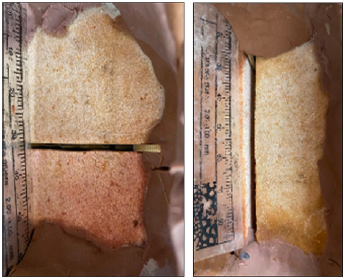
Preparación de la muestra: la muestra fue impermeabilizada sin afectar la zona de contacto con el fluido, utilizando una resina química que al mezclarse con un catalizador se endurece al secarse y deja una superficie completamente lisa en las paredes externas de la muestra (Figura 3).
Diseño de fractura: se diseñó la fractura, con continuidad vertical, ancho de fractura de 1,7 mm y 2,2 mm y una longitud de 60 mm como se observa en la Figura 4.
Diseño de lodos: se diseñaron dos lodos, el primero con mayor contenido de bentonita, esto con el fin de incrementar el valor de la viscosidad, medida en el viscosímetro de Fann.
Reología del lodo: se tomaron lecturas de esfuerzo de corte a 9300 y 9600 para cada lodo. Luego se calculó la viscosidad aparente (VA) a través de la ecuación 14
Posteriormente, se realizó el cálculo de la viscosidad plástica (VP) ecuación 15.
La viscosidad plástica también depende de la viscosidad de la fase fluida, cuando la viscosidad del agua disminuye a medida que aumenta la temperatura, la viscosidad plástica disminuye proporcionalmente. Lo anterior es importante mencionarlo ya que en yacimientos geotérmicos se caracterizan por tener presencia de fracturas. El cálculo del punto de cedencia o Yield Point (YP) se realizó de acuerdo a la ecuación 16 descrita como:
La Tabla 3 muestra los valores de reología calculados y con los valores del viscosímetro de lodo a ϴ300 y ϴ600.
Tabla 3 Propiedades reológicas de lodos de perforación diseñados en laboratorio.
| Propiedades reológicas | Lodo 1 | Lodo 2 |
|---|---|---|
| Cantidad de Bentonita (g) | 95 | 80 |
| Lectura Viscosímetro de lodo ϴ 600 (lb/ft2) | 41 | 26 |
| Viscosímetro de lodo ϴ 300 (lb/ft2) | 27 | 15 |
| Viscosidad aparente | 20,5 | 13 |
| Velocidad de rotación RPM (ω) | 600 | 600 |
| Velocidad de corte Υ (1/seg) | 1021,8 | 1021,8 |
| Esfuerzo cortante (t) en (lb /100 ft2) | 43,7798 | 27,7628 |
| Viscosidad plástica PV (Cp) | 14 | 11 |
| Yield Point (YP) (lb /100 ft2) | 13 | 4 |
Fase de aplicación
Se realizaron tres ensayos por cada lodo de perforación, cada ensayo consistió en:
Paso 1: Verter lodo sobre la fractura, asegurando que siempre estuviera cubierta de lodo, simulando el hecho de que la cara de pozo siempre está expuesta al lodo, hasta colocar revestimiento.
Paso 2: El flujo será generado por efecto de la gravedad a presión atmosférica. El volumen ingresado fue de 1,0 L
Paso 3: Se divide el lodo en recipientes de 0,25 L, 0,5 L, 0,75 L y 1,0 L.
Paso 4: Con la ayuda de un cronómetro, se toma el tiempo que se demora en pasar cada uno de los volúmenes, realizando la toma 3 veces y promediando los resultados
Paso 5: El lodo es recolectado cada vez que pasa a través de la fractura y medido para confirmar que no se hayan generado pérdidas.
La Figura 5 muestra la entrada y salida del fluido de perforación a través de la fractura.
Resultados
Los resultados de los ensayos se presentan en las Tablas 4 a la 7 (los resultados se reportan en litros por facilidad de comprensión. Un litro equivale a 0,001 m3). Estos valores muestran que el lodo 1, es decir, el que tiene valores de viscosidad más altos en comparación con el lodo 2, tarda mayor tiempo en circular por la fractura. Es importante resaltar que después de cada ensayo se cuantificó el lodo para medir la pérdida de fluido a través de la matriz, pero en todos los casos el fluido circuló únicamente por la fractura manteniendo la misma cantidad de volumen inicial.
Tabla 4 Resultados del lodo 1 en la fractura de 1,7 mm.
| Lodo 1 | |||||||
|---|---|---|---|---|---|---|---|
| Prueba 1 | Prueba 2 | Prueba 3 | Promedio | ||||
| Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) |
| 1 | 1012 | 1 | 781 | 1 | 876 | 1 | 889,7 |
| 0,75 | 657 | 0,75 | 669 | 0,75 | 760 | 0,75 | 695,3 |
| 0,5 | 468 | 0,5 | 396 | 0,5 | 481 | 0,5 | 448,3 |
| 0,25 | 189 | 0,25 | 206 | 0,25 | 199 | 0,25 | 198,0 |
Tabla 5 Resultados del lodo 2 en la fractura de 1,7 mm.
| Lodo 2 | |||||||
|---|---|---|---|---|---|---|---|
| Prueba 1 | Prueba 2 | Prueba 3 | Promedio | ||||
| Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) |
| 1 | 361 | 1 | 293 | 1 | 280 | 1 | 311,3 |
| 0,75 | 272 | 0,75 | 205 | 0,75 | 202 | 0,75 | 226,3 |
| 0,5 | 179 | 0,5 | 125 | 0,5 | 63 | 0,5 | 122,3 |
| 0,25 | 74 | 0,25 | 82 | 0,25 | 59 | 0,25 | 71,7 |
Tabla 6 Resultados del lodo 1 en la fractura de 2,3 mm.
| Lodo 1 | |||||||
|---|---|---|---|---|---|---|---|
| Prueba 1 | Prueba 2 | Prueba 3 | Promedio | ||||
| Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) |
| 1 | 133 | 1 | 113 | 1 | 128 | 1 | 124,7 |
| 0,75 | 92 | 0,75 | 82 | 0,75 | 79 | 0,75 | 84,3 |
| 0,5 | 55,12 | 0,5 | 53 | 0,5 | 58 | 0,5 | 55,4 |
| 0,25 | 31,1 | 0,25 | 28 | 0,25 | 31 | 0,25 | 30,0 |
Tabla 7 Resultados del lodo 2 en la fractura de 2,3 mm.
| Lodo 2 | |||||||
|---|---|---|---|---|---|---|---|
| Prueba 1 | Prueba 2 | Prueba 3 | Promedio | ||||
| Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) |
| 1 | 81 | 1 | 87 | 1 | 76 | 1 | 81,3 |
| 0,75 | 64 | 0,75 | 67 | 0,75 | 61 | 0,75 | 64,0 |
| 0,5 | 48 | 0,5 | 39,3 | 0,5 | 32,3 | 0,5 | 39,9 |
| 0,25 | 15,5 | 0,25 | 18,13 | 0,25 | 15,6 | 0,25 | 16,4 |
Así como se implementa el modelo físico, también se utiliza la ecuación 5 y se calcula el perfil de velocidad promedio para cada lodo y fractura como se detalla en la Tabla 8:
Para la aplicación de la ecuación 5, se sigue el siguiente procedimiento.
• Calcular los valores de k y n a partir de las lecturas reológicas registradas en la Tabla 3.
• El diferencial de presión solo estará dado por la presión atmosférica y el producto de la densidad por la gravedad.
• El ancho de fractura se toma el indicado en la fase de diseño mencionada en el ítem Diseño de fractura. Con la velocidad promedio, el área de entrada de fluido que es el producto del ancho de fractura por la longitud de la fractura (w*L) y diferentes tiempos, se calcula el caudal de flujo a través de la misma.
Tabla 8 Resultados de implementar la ecuación 5.
| Lodo 1 ancho 1,7 mm | Lodo 1 ancho 2,3 mm | Lodo 2 ancho 1,7 mm | Lodo 2 ancho 2,3 mm | ||||
|---|---|---|---|---|---|---|---|
| Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) | Volumen (L) | Tiempo (s) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,04 | 50 | 0,05 | 10 | 0,16 | 50 | 0,11 | 10 |
| 0,08 | 100 | 0,09 | 20 | 0,31 | 100 | 0,22 | 20 |
| 0,12 | 150 | 0,14 | 30 | 0,47 | 150 | 0,33 | 30 |
| 0,16 | 200 | 0,18 | 40 | 0,63 | 200 | 0,44 | 40 |
| 0,2 | 250 | 0,23 | 50 | 0,78 | 250 | 0,55 | 50 |
| 0,25 | 300 | 0,27 | 60 | 0,94 | 300 | 0,65 | 60 |
| 0,29 | 350 | 0,32 | 70 | 1,1 | 350 | 0,76 | 70 |
| 0,33 | 400 | 0,37 | 80 | 1,25 | 400 | 0,87 | 80 |
| 0,37 | 450 | 0,41 | 90 | 0,98 | 90 | ||
| 0,41 | 500 | 0,46 | 100 | ||||
| 0,45 | 550 | 0,5 | 110 | ||||
| 0,49 | 600 | 0,55 | 120 | ||||
| 0,53 | 650 | 0,59 | 130 | ||||
| 0,57 | 700 | ||||||
| 0,61 | 750 | ||||||
| 0,65 | 800 | ||||||
| 0,69 | 850 | ||||||
| 0,74 | 900 | ||||||
Discusión de resultados
Tomando los resultados experimentales de las Tablas 4 - 7 y los resultados teóricos de la ecuación 5 definida para ley de potencia, documentados en la Tabla 8.
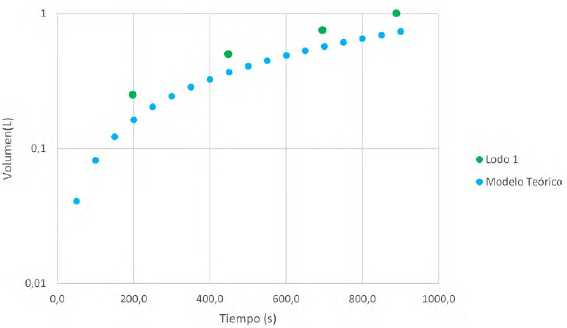
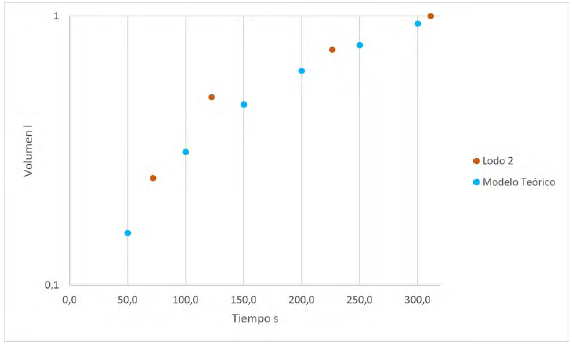
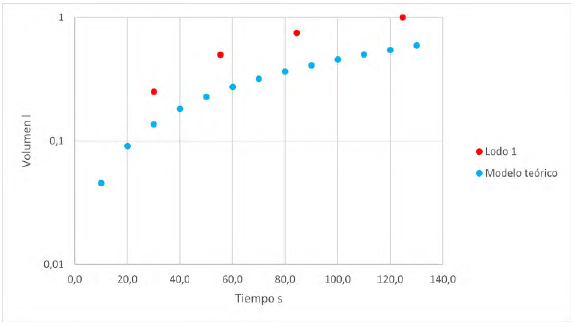
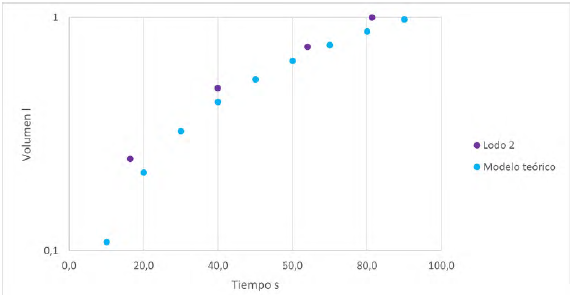
Se realizan las comparaciones comprobando que el modelo numérico sí representa el modelo físico (Figura 6 -9).
Para las Figuras 6 y 7 que corresponden a la fractura de 1,7 mm, se observa un excelente ajuste en el volumen acumulado que pasa a través de la fractura, especialmente para el lodo 2 de menor viscosidad con un error del 3%. Para el caso de la fractura de 2,3 mm, lodo 2, también se presenta un buen ajuste con un error del 9%. Para el lodo 1 hay una diferencia en el ajuste cercana al 35%, aunque la tendencia se mantiene. Lo anterior se puede deber al efecto de la rugosidad de las paredes de fractura. Ozdemirtas et al. (2007) con ayuda de la teoría de lubricación de Reynolds, analizan la rugosidad superficial y el ancho de la fractura, apoyados en datos de laboratorio de muestras de areniscas de Berea, limestone de Indiana y granito, concluyendo que la rugosidad disminuye las pérdidas de fluido. Así mismo, Lavrov (2013) en su investigación concluye que, en una fractura de paredes rugosas, la apertura hidráulica equivalente disminuye. Lo anterior soporta que el valor teórico de la Figura 6 y 8 para lodo más viscoso, es inferior al dato experimental, ya que faltaría incluir corrección en el modelo por rugosidad. Esto es más evidente para lodos viscosos que se dificulta más su movimiento.
Para lodos de baja viscosidad o newtonianos el efecto es inferior como se observa en las Figuras 7 y 9, aun así, se recomienda también realizar corrección por rugosidad. En conclusión, se puede confirmar que el modelo reproduce el fenómeno real. Por lo anterior, este modelo puede ser utilizado para reproducir escenarios de pérdidas de lodo en campo, en función de estudios de caracterización de fracturas y fallas como es el caso reportado por Mejía et al. (2012) quienes describen las fallas presentes en una zona con potencial de energía geotérmica.
Conclusiones
El modelo físico realizado, mostró el flujo de lodo a través de una fractura en una muestra de roca, evitando así el escalado del material. La presión y la gravedad son variables que en el modelo y en la realidad tienen una relación uno a uno, lo que facilita su análisis. La densidad de lodo fue escalada en laboratorio.
La metodología que combina el modelo matemático con el modelo físico mostró una buena correlación entre los resultados, confirmando que es válida para analizar diferentes tipos de fluido.
El experimento y su correlación con el modelo numérico permite proponer una metodología, para una vez convertidos los datos a coordenadas radiales, analizar escenarios reales de pérdidas de lodo a través de fracturas en campo.
La rugosidad puede afectar la estimación teórica de las pérdidas de lodo a través de fracturas, por tanto, se recomienda hacer la corrección cuando se realicen escalados a campo.