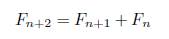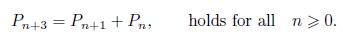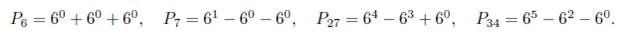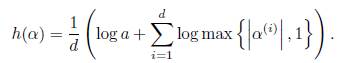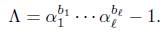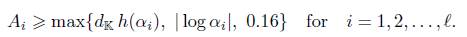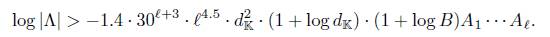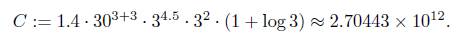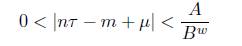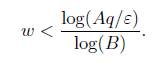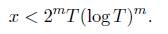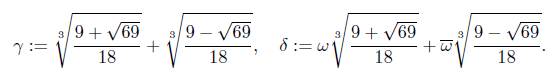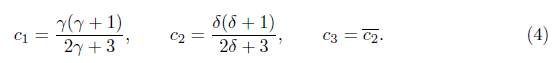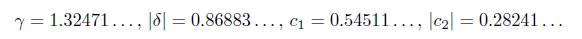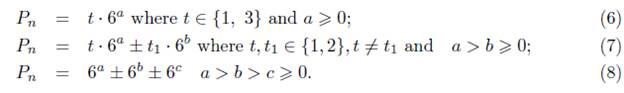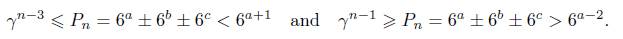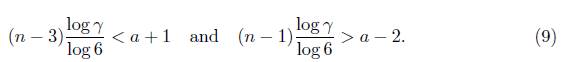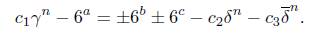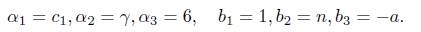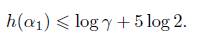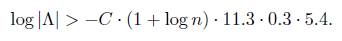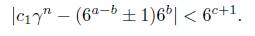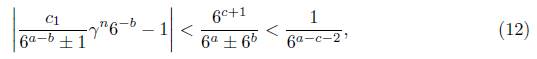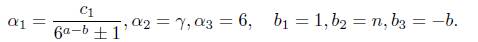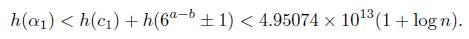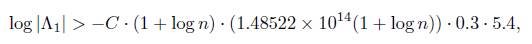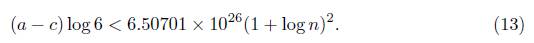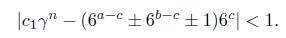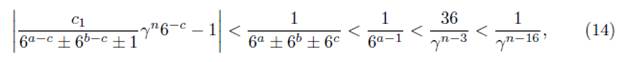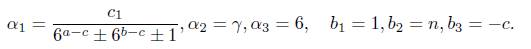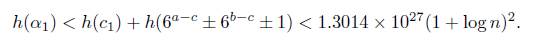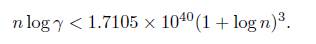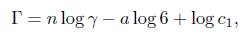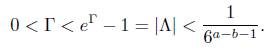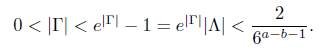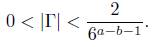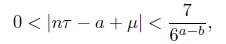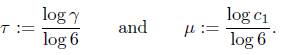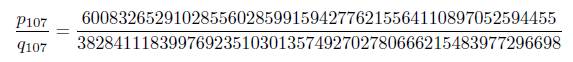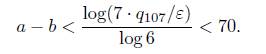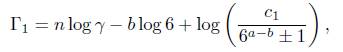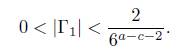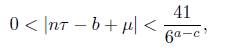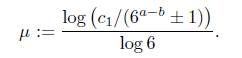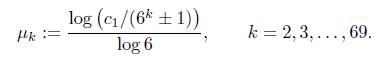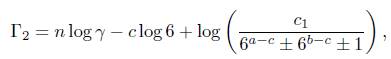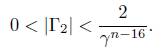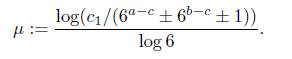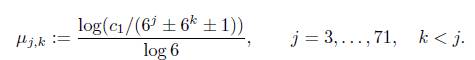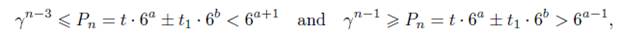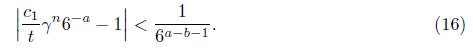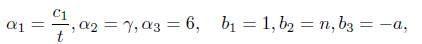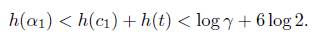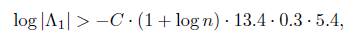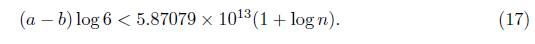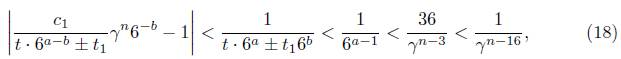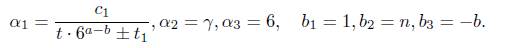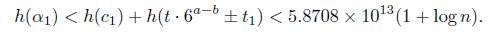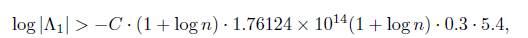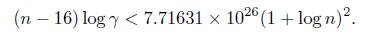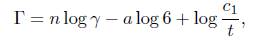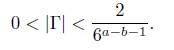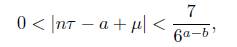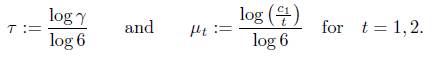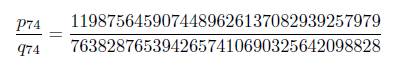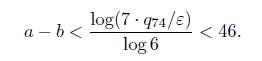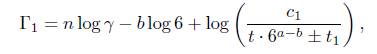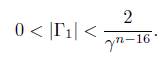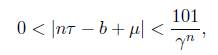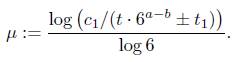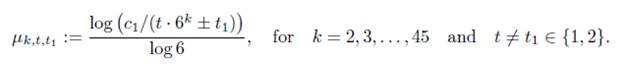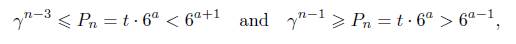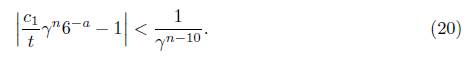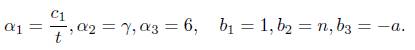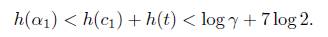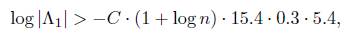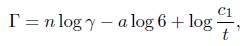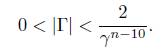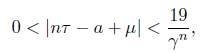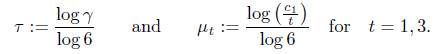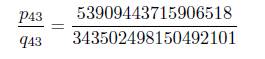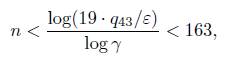1. Introduction
Let (Fn)n≥0 be the Fibonacci sequence. It is given by the initial conditions F0 = 0, F1 = 1 and the recurrence formula
holds for all n≥0. Let’s consider the Diophantine equation
in positive integers (n, x, a, b) with max{a, b}≥2. The case x = p with p being a prime number is studied in [9] by Luca and Szalay. They show that such an equation has only finitely many solutions. Then, the same conclusion is obtained by Laishram and Luca in [7] where this time x is of the form pcqd where p and q are prime numbers. In [6], the particular case x = 2 was completely solved.
There are many other instances of Diophantine equations of the same flavour as the above one. For example, in [8] the Diophantine equation Fn = pa ± pb, where p is prime number, is studied. And, in [12] the squares of the form 2a ± 2b ± 2c are found.
Now, let us consider the Padovan sequence (Pn)n≥0, named after the architect R. Padovan. It is the ternary recurrence sequence given by P0 = 0, P1 = P2 = 1 and the recurrence formula
This is A000931 sequence in [11]. Its first few terms are
0, 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, ...
Motivated by the above problems, in this note we study the Diophantine equation
in the non-negative integers (n, a, b, c) with α≥b≥c≥0. To avoid numerical repeated solutions we will assume that n # 1, 2, 4. Note that for all non-negative integer a, (3, α, α, 0) is clearly a solution to the case Pn = 6a − 6b + 6c with a = b. Let us call these trivial solutions of equation (2). Our result is the following:
Theorem 1.1. All non trivial solutions of equation (2) in non-negative integers (n, a, b, c) with n # 1, 2, 4 and α≥b≥c≥0 are
2. Linear forms in logarithms, reduction method
In proving Theorem 1.1 we use lower bounds for linear forms in logarithms, and we use the result due to Matveev explained in Theorem 2.1. Let α be an algebraic number of degree d, let α > 0 be the leading coefficient of its minimal polynomial over ℤ and let α = α1, ..., α(d) denote its conjugates. The logarithmic height of α is defined as
The basic properties of the function h are the following. For α, β algebraic numbers and m ∈ ℤ we have
Now, let K be a real number field of degree dK, α1, . . . , αℓ ∈ K positive elements and b1, . . . , bℓ ∈ ℤ \ {0}. Let B ⩾ max{|b1|, . . . , |bℓ|} and
Let A1, . . . , Aℓ be real numbers with
The following result is due to Matveev in [10] (see also Theorem 9.4 in [2]).
Theorem 2.1. (Matveev’s Theorem) Assume that Λ # 0. Then
In this paper we always use ℓ := 3. Further K := Q(γ), where γ is given at the beginning of Section 3, has degree d K = 3. So, once and for all we fix the constant
Our second tool is a version of the reduction method of Baker-Davenport based on the lemma in [1]. We shall use the following one given by Bravo, Gómez and Luca in [3] (see also [4]). For a real number x, we write ∥x∥ for the distance from x to the nearest integer.
Lemma 2.2. Let M be a positive integer. Let τ, µ, A > 0, B > 1 be given real numbers. Assume that p/q is a convergent of τ such that q > 6M and ε := ∥µq∥ − M∥τ q∥ > 0. If (n, m, w) is a positive solution to the inequality
with n ≤M then
Finally, the following result of Guzmán and Luca [5] will be very useful.
Lemma 2.3. If m≥1, T > (4m2)m and T > x/(log x)m. Then
3. Proof of Theorem 1.1
Let us to start with some basic properties of the Padovan sequence. For a complex number z we write
It is clear that γ, δ,
which holds for all n ⩾ 0, where
Formula (3) follows from the general theorem on linear recurrence sequences since the above polynomial is the characteristic polynomial of the Padovan sequence. We note that
Further, the inequalities
hold for all n≥1. These, formula (3) and inequalities (5) can be proved by induction.
Observe that the study of the non-trivial solutions of equation (2) reduces to the study of equations of the following form:
An elementary analysis shows that the right hand side of each these equations is always positive. So, we assume n≥1. As n # 1, 2, 4, we assume throughout the proof that n≥3 with n # 4. The most involved case is equation (8), so we start with it.
3.1. Case (8)
Recall that n≥3, n # 4 and a > b > c≥0. From inequalities (5) we obtain
So,
In particular note that α ≤ n since (log γ/ log 6) < 1. Now, if n≤500 from (9) we see that α ≤80. Running a computer basic program in the range 0≤n≤500, ≤0 c < b < α ≤80 we find the last two solutions written in Theorem 1.1. We will prove that these are all of them in this case.
From now on, we assume n > 500. In this case, (9) gives α ≥ 76. The first task is to obtain an absolute upper bound on n. To this end, from the Binet formula (3) we rewrite our equation as
Dividing through by 6a, we obtain
Let Λ be the expression inside in the left hand side of (10). Now, if Λ = 0 then c1γn = 6a and, by taking norms we conclude that the norm of c1 is an integer which is not. The norm of c1 is 1/23. Hence Λ # 0 and we apply Matveev’s inequality to it by taking
Thus B = n. The heights h(α2), h(α3) are log γ/3 and log 6, respectively. For α1 we use the properties of the height to conclude
Thus, we take A1 = 11.3, A2 = 0.3, and A3 = 5.4. Then,
Comparing this with (10), we obtain
Again, from the Binet formula (3) we rewrite (2) and obtain
Dividing through by 6a ± 6b we get
where we use 6a ± 6 b > 6a−1. Let Λ1 be the expression inside of the absolute value on the left side of (12). With an argument as given for Λ above, we see that Λ1 # 0 and we apply Matveev’s to it. To do this, we consider
Thus, B = n. The heights of α2 and α3 are already calculated. For α1, we again use the properties of the height and (11) to conclude that
So we take A1 = 1.48522 × 1014(1 + log n) and A2, A3 as above. Hence, from Matveev’s inequality we obtain
which compared with (12) yields
In particular, since b < a, we also have an upper bound on (b − c) log 6.
Finally, from the Binet formula (3) we rewrite again (2) and obtain
Dividing through by 6a ± 6b ± 6c we get
where we use 6a+1 > γ n−3 from (9). Let Λ2 be the expression inside of the absolute value on the left side of (14). As above, Λ2 # 0 and we apply Matveev’s inequality to it. Now, we consider
Thus, B = n. The heights of α2 and α3 are already calculated. For α1, from (13) we have
So we take A1 = 3.9042 × 1027(1 + log n)2 and A2, A3 as above. Hence, from Matveev’s inequality we obtain
which compared with (14) yields
Thus, n < 4.86629 × 1041(log n)3 and from Lemma 2.3 we get the following absolute upper bound on n:
Now, the second step is to reduce this upper bound on n. To do this, we consider
and go to (10). Assume that α − b > 1. Note that eΓ − 1 = Λ # 0. Thus, Γ # 0. If Γ > 0, we have that
If on the other hand, Γ < 0, we then have that 1 − eΓ = |Λ| < 1/2. Thus, eΓ < 2. Hence,
Thus, in both cases, we have
Dividing through by log 6, we obtain
Where
Now, we apply Lemma 2.2. To do this, we take M = 3.44305 × 1048, which from (15) is the upper bound on n. With the help of Mathematica, we found that the convergent
of τ is such that q107 > 6M and ε = ||q107 · µ|| − M||q107 · τ|| = 0.284414 > 0. Thus from Lemma 2.2, with A := 7 and B := 6, we obtain that
Now, consider
and go to (12). Assume that a − c > 2. Note that eΓ1 − 1 = Λ1 # 0. Thus, Γ1 ̸= 0. As in the above case by considering again the cases Γ1 > 0 and Γ1 < 0 we conclude that
Dividing through by log 6, we obtain
where τ is as above and
Consider
With Mathematica we find again that the 107−th convergent of τ is such that q107 > 6M and εk ≥ 0.0162182 for all k = 2, ..., 69. We calculated log(q107 · 41/εk)/ log 6 for all k = 2, . . . , 69 and found that the maximum of these values is at most 71. Therefore α − c ≤71.
Finally, consider
and go to (14). Note that eΓ2 − 1 = Λ2 # 0. Thus, Γ2 # 0. Again as above, we can conclude that
Dividing through by log 6, we obtain
where, τ is as above and
Consider
Again, the 107-th convergent of τ is such that q107 > 6M and εj,k ≥ 0.0000191955 for all j = 3, . . . , 71, k < j. Finally, by calculating log(q107 · 101/εj,k)/ log γ for all these cases we find that the maximum of these values is at most 485. Therefore n ≤ 485 which contradicts the assumption on n and finish the proof of this case.
3.2. Case (7)
This case also follows the same lines of argument as in Case (8). So, we will not write all detailed calculations but only the result of the step.
As above, n ≥ 3, n # 4; t, t1 ∈ {1, 2}, t # t1 and a > b ≥0. The inequalities
where t, t1 ∈ {1, 2} and t # t1, show that we can and we will use the same inequalities given in (9). In particular a n and with a basic computer program in the intervall 0 ≤ n ≤ 350 and 0≤ b < α ≤ 55 we obtain the solution P7 = 61 − 2 · 60 = 61 − 60 − 60 for this case written in Theorem 1.1. As above, we now show it is the only one.
Let n > 350. Thus α > 53. As above, from Binet’s formula equation (7) gives
Let Λ be the expression inside of the absolute value on the left side of (16). Now, being Λ # 0 we take
and apply Matveev’s to it. So, B = n. We already know the heights of α2 and α3 and for α1 we have
So we take A1 = 13.4 and A2 = 0.3, A3 = 5.4. Hence, from Matveev’s inequality we get
which compared with (16) yields
From the Binet formula (3) we rewrite again (7) and obtain
where we use 6a+1 > γ n−3 from (9). Let Λ1 be the expression inside of the absolute value on the left side of (18). Again, being Λ1 # 0 we consider
and apply Matveev’s inequality with B = n. We know the heights of α2 and α3 and for α1, (17) gives
So we take A1 = 1.76124×1014(1+log n) and A2, A3 as above. Then Matveev’s inequality gives
which compared with (18) yields
Thus, n < 1.09763 × 1028(log n)2 and from Lemma 2.3 we get the following absolute upper bound on n:
Now we reduce this upper bound on n. Consider
and go to (16). Assume that α − b > 1. Note that eΓ − 1 = Λ # 0. Thus, Γ # 0 and with the same above analysis we find that
Dividing through by log 6, we obtain
Where
With M = 1.83028 × 1032 Mathematica finds that the 74-th convergent
of τ is such that q74 > 6M and εt = ||q74 · µt|| − M ||q74 · τ || > 0.107923 > 0 for t = 1, 2. Thus from Lemma 2.2, with A := 7 and B := 6, we obtain that
Now consider
and go to (18). Then Γ1 # 0 and we have
Dividing through by log 6, we obtain
where τ is as above and
Let
Again, Mathematica finds that the 74-th convergent of τ is such that q74 > 6M and εk,t,t1 ≥ 0.00798086 for all k = 2, . . . , 45 and t # t1 ∈ {1, 2}. Then the maximum of the log(q74 · 101/εk,t,t1 )/ log γ for all k = 2, . . . , 45 and t # t1 ∈ {1, 2} is at most 311. So, n ≤311 which contradicts the assumption on n and finish the proof of this case.
3.3. Case (6)
Again, n ⩾ 3, n # 4. Now t ∈ {1, 3} and a ⩾ 0. We have the inequalities
where t ∈ {1, 3}. So, we use the same inequalities given in (9). Then a ⩽ n. In the interval 0 ⩽ n ⩽ 200 and 0 ⩽ a ⩽ 32 Mathematica gives the solution P6 = 3 ・ 60 = 60 + 60 + 60 listed in Theorem 1.1. We prove it is the only one in this case.
Let n > 200. Thus a > 29. From Binet’s formula equation (6) gives
Let Λ be the expression inside of the absolute value on the left side of (20). As Λ # 0 we take
and apply Matveev’s inequality to it with B = n. The height of α1 is
So we take A1 = 15.4 and A2 = 0.3, A3 = 5.4 as above. Hence, from Matveev’s inequality we obtain
which compared with (20) and Lemma 2.3 yields
Now, consider
and go to (20). Note that eΓ − 1 = Λ # 0. Thus, Γ # 0 and we obtain in fact that
Dividing through by log 6, we obtain
Where
Now, with M = 3.24438 × 1016 Mathematica find that the 43-th convergent
of τ is such that q43 > 6M and εt = ||q43 · µt|| − M||q43 · τ|| > 0.087677 > 0 for t = 1, 3. Thus from Lemma 2.2, with A := 19 and B := γ, we obtain that
which contradicts the assumption on n and finish the proof of this case. This finish the proof of Theorem 1.